توزیع پواسون و حل مسائل مرتبط با کدهای R — از صفر تا صد

در یکی از مطالب فرادرس با عنوان متغیر تصادفی و توزیع پواسون — به زبان ساده با این توزیع آشنا شدیم. در این نوشتار سعی می‌کنیم به کمک کدهای زبان برنامه نویسی R، مسائلی که با توزیع پواسون در ارتباط هستند را معرفی کرده و به حل آن‌ها بپردازیم.

همانطور که می‌دانید، توزیع پواسون، دارای تکیه‌گاه به صورت $$S=\{0,1,2,\cdots\}$$ است. پس یک توزیع گسسته محسوب می‌شود. تابع احتمال برای این توزیع بیانگر تعداد رخدادها (موفقیت) در یک بازه زمانی ثابت یا مکان محدود است به شرطی که نرخ رخداد این پیشامدها مستقل از یکدیگر باشد.

در ادامه با استفاده از کدهای زبان R مفهوم و شیوه محاسبه احتمال برای متغیر تصادفی پواسون را بهتر درک خواهیم کرد.

آشنایی با توزیع پواسون به کمک کدهای R

از آنجایی که می‌خواهیم از کدهای R‌ استفاده کنیم، بهتر است ابتدا محیط کاری را در این برنامه آماده سازیم. در اینجا برای انجام محاسبات، از کتابخانه‌های مختلفی استفاده خواهیم کرد که در ادامه با آن‌ها آشنا خواهیم شد. اولین کتابخانه، بسته (tidyverse) است که به منظور نمایش داده‌ها به کار می‌رود.

فیلم آموزش تحلیل داده ها با نرم افزار مینی تب Minitab – مقدماتی در فرادرس

کلیک کنید

همچنین برای کار روی داده‌ها از کتابخانه (lubridate) استفاده خواهیم کرد. بنابراین بهتر است ابتدا این کتابخانه‌ها را با استفاده از دستور install.package نصب و به کمک دستورات زیر بارگذاری کنیم.

1install.packages("tidyverse")
2install.packages("lubridate")
3library(tidyverse) # Data Wrangling and Visualization
4library(lubridate) # Date Manipulation

داده و اطلاعات

در این نوشتار از داده‌های مربوط به مسابقات فوتبال استفاده می‌کنیم که از سال‌های 1827 تا 2018 جمع‌آوری شده است. تعداد رکوردهای این بانک اطلاعاتی حدود 39هزار سطر است. فایل فشرده مربوط به این داده‌ها را می‌توانید از اینجا (+) دریافت کنید. با اجرای فرمان زیر می‌توانید این فایل را فراخوانی کنید و نمایش دهید.

1library(readr)
2results <- read_csv("fifa-result.zip")
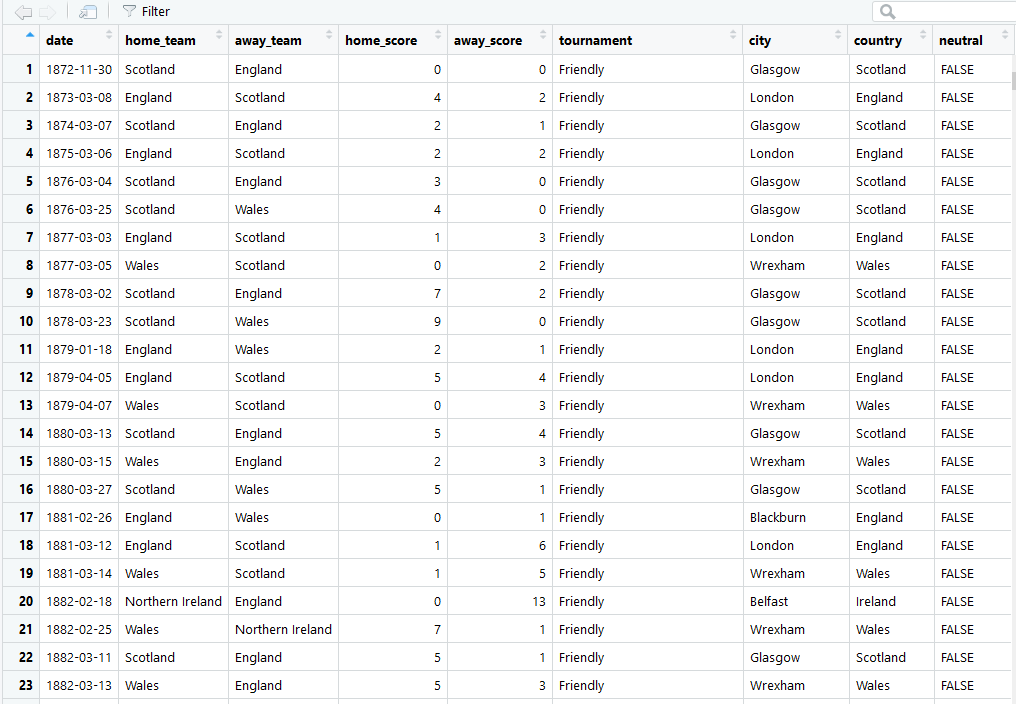
3View(results)

با اجرای این دستورات، خروجی به صورت زیر خواهد بود که شامل جدول اطلاعاتی مورد نظر است.

مشخص است که ستون‌های جدول، اسامی متغیرها و سطرها مقدارهای مربوط به متغیرها هستند. ابتدا بهتر است داده‌ها را بررسی کنیم. متغیرهای موجود در این بانک اطلاعاتی به ترتیب به صورت زیر هستند:

• date: تاریخ انجام مسابقه
• home_team: تیم میزبان
• away_team: تیم میهمان
• home_score: گل‌های تیم میزبان
• away_score: گل‌های تیم میهمان
• tournament: نوع مسابقه
• city: شهر محل مسابقه
• country: کشور محل مسابقه
• neutral: انجام بازی در شهر یا کشور بی‌طرف (محل مسابقه، خارج از شهر یا کشور میزبان یا میهمان بوده است.)

با توجه یه این متغیرها و داده‌های موجود می‌توان در نگاه اول به نتایج زیر رسید:

1. این اطلاعات از ۳۰ نوامبر 1872 تا 10 جولای 2018 اطلاعات جمع‌آوری شده‌اند.
2. حداکثر امتیازات خانگی ۳۱ و امتیازات خارج از خانه برابر با ۲۱ است.
3. ۲۵٪ مسابقات در مناطق بی‌طرف برگزار شده است. (برای مثال جام‌های جهانی)

این محاسبات را به کمک مرتب سازی داده‌ها و یا جمع‌بندی می‌توان بدست آورد. البته کدهای زیر نیز می‌تواند چنین اطلاعاتی را در اختیارتان قرار دهد.

1max(results$date)
2min(results$date)
3max(results$home_score)
4max(results$away_score)
5sum(results$neutral==TRUE)/nrow(results)

از آنجایی که برای تحلیل این داده‌ها به مقدارهای سال و ماه نیاز داریم باید با استفاده از کدهای زیر این مقادیر را از متغیر date استخراج و به متغیری از نوع «عامل» (factor) تبدیل کنیم.

1results = results %>% 
2  mutate(year = as.factor(year(date)),
3         month = as.factor(month(date)),
4         totalGoals = home_score + away_score,)

همچنین جمع گل‌های هر بازی را در متغیر totalGoals ثبت کرده‌ایم.

به کارگیری توزیع پواسون

برای آن که متغیر تصادفی X دارای توزیع پواسون باشد، وجود چهار شرط برایش ضروری است. در ادامه به معرفی این شرط‌ها می‌پردازیم و در نهایت به شکلی از تعریف متغیر تصادفی مربوط به گل‌های زده می‌رسیم که دارای توزیع پواسون خواهد بود.

1. X تعداد دفعاتی است که یک پیشامد در یک بازه یا فاصله زمانی یا مکانی رخ می‌دهد. بنابراین تکیه‌گاه آن اعداد صحیح نامنفی است. یعنی داریم $$X=0,1,2,\cdots$$
2. رخداد یک پیشامد، روی احتمال رخداد پیشامد دیگر تاثیر گذار نیست. به این ترتیب پیشامدها مستقل هستند.
3. نرخ رخداد پیشامدها ثابت است. در هر بازه یا فاصله زمانی یا مکانی، نرخ رخداد پیشامد کاهش یا افزایش نمی‌یابد.
4. دو پیشامد در یک زمان رخ نمی‌دهند. یک پیشامد دارای دو وضعیت رخداد (۱) و عدم رخداد (۰) است که در هر زیرفاصله کوچک تعیین می‌شود.

حال اجازه دهید که مقدار متغیر تصادفی X و مفهوم بازه یا فاصله را در مسئله خودمان، برای سه حالت در نظر بگیریم.

1. با فرض X تعداد کل گل‌ها در یک بازه یکساله است.
2. با فرض X تعداد کل‌ گل‌ها در یک بازه ۱ روزه است.
3. با فرض X تعداد کل گل‌ها در فاصله انجام یک مسابقه است.

مشخص است برای این سه حالت شرط‌های ۱ و ۲ صادق هستند ولی برای بررسی شرط‌های ۳ و ۴ احتیاج به بررسی بیشتر است.

I- با فرض X تعداد کل گل‌ها در یک بازه یکساله

در ادامه سعی می‌کنیم، با فرض اینکه X یک متغیر تصادفی است که تعداد گل‌ها در یک بازه یکساله را شمارش می‌کند، ارتباط X را با توزیع پواسون مورد بررسی قرار دهیم. با استفاده از کدهای زیر نمودارهایی ایجاد کرده و صحت شرط‌های ۳ و ۴ را برای این حالت تحقیق می‌کنیم.

1results %>% 
2  group_by(year) %>% 
3  summarise(mean(totalGoals), sum(totalGoals), min(totalGoals), max(totalGoals), median(totalGoals))

به این ترتیب میانگین، جمع، حداقل، حداکثر و میانه برای کل گل‌های زده شده برحسب سال محاسبه می‌شود.

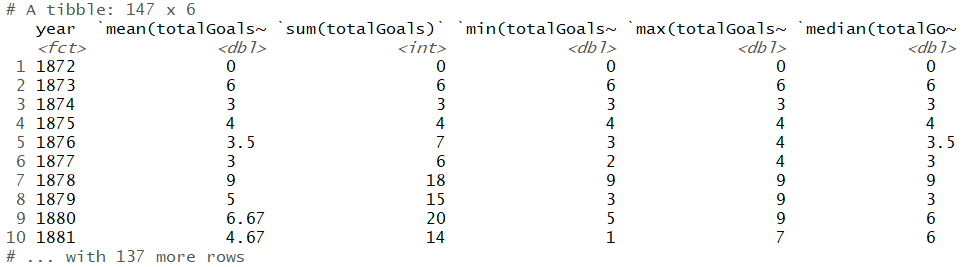
همچنین نمودار مربوط به میانگین گل‌های زده به تفکیک سال به کمک کد زیر، ظاهر می‌شود.

1results %>% 
2  group_by(year) %>% 
3  summarise(meanGoals = mean(totalGoals)) %>% 
4  ggplot(aes(x=year, y=meanGoals)) + 
5  geom_col(fill = "purple") +
6  labs(x = "Year", y = "Mean Number of Goals",
7       title = "Yearly Mean Number of Goals in soccer",
8       caption = "Data Source: https://www.kaggle.com/martj42/international-football-results-from-1872-to-2017") + 
9  theme(panel.background = element_blank(),
10        panel.grid.minor = element_line(colour = "grey"),
11        axis.text.x=element_blank(),
12        axis.ticks.x=element_blank())

با اجرای این کدها، خروجی به صورت نمودار زیر خواهد بود.

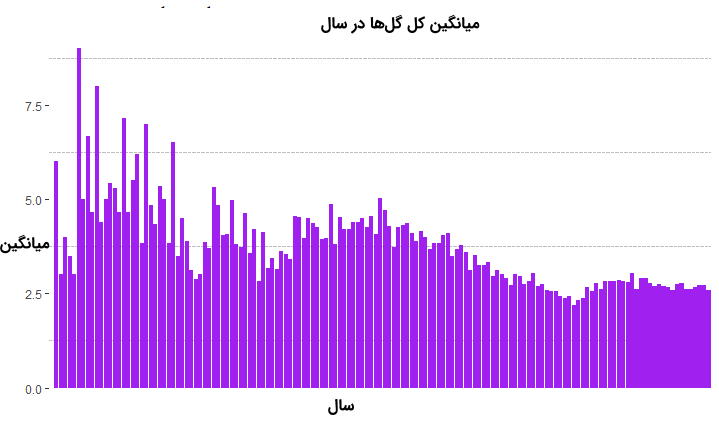
به همین ترتیب برای مجموع گل‌های زده شده در مسابقات به تفکیک سال نیز از کد زیر استفاده خواهیم کرد.

1results %>% 
2  group_by(year) %>% 
3  summarise(numGoals = sum(totalGoals)) %>% 
4  ggplot(aes(x=year, y=numGoals)) + 
5  geom_col(fill = "blue") +
6  labs(x = "Year", y = "Total Number of Goals",
7       title = "Yearly Total Number of Goals in soccer",
8       caption = "Data Source: https://www.kaggle.com/martj42/international-football-results-from-1872-to-2017") + 
9  theme(panel.background = element_blank(),
10        panel.grid.minor = element_line(colour = "grey"),
11        axis.text.x=element_blank(),
12        axis.ticks.x=element_blank())

با اجرای این دستورات، نموداری به صورت زیر نمایش داده خواهد شد. همانطور که در هر دو نمودار دیده می‌شود، کم و بیش میانگین گل‌های زده شده در هر سال تقریبا با یکدیگر برابر هستند. اما مجموع گل‌های زده شده، براساس سال، رو به افزایش است. این مسئله، باعث می‌شود که متغیر تصادفی X با تعریف تعداد گل‌های زده در سال، در شرط سوم برای توزیع پواسون صدق نکند.

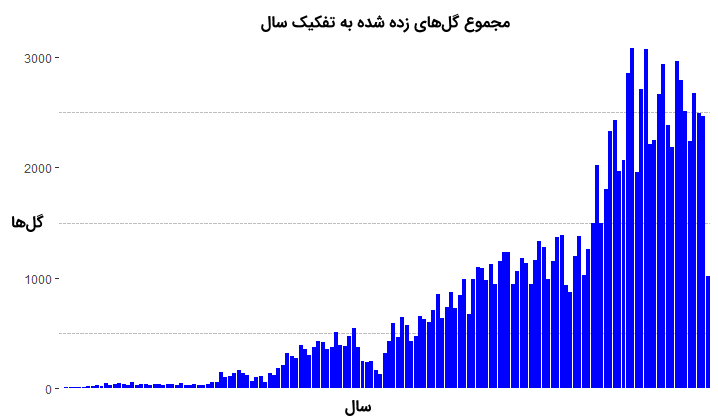
همانطور که در هر دو نمودار دیده می‌شود، کم و بیش میانگین گل‌های زده شده در هر سال تقریبا با یکدیگر برابر هستند. اما مجموع گل‌های زده شده، براساس سال، رو به افزایش است. این مسئله، باعث می‌شود که متغیر تصادفی X با تعریف تعداد گل‌های زده در سال، در شرط سوم برای توزیع پواسون صدق نکند.

از طرفی، در توزیع پواسون، تعداد آزمایش‌ها باید بیشتر از تعداد موفقیت‌ها باشد. ولی در اینجا تعداد آزمایش‌ها برابر با ۱۴۷ یعنی تعداد سال‌ها است در حالیکه تعداد موفقیت‌ها که تعداد گل‌ها است بسیار بیشتر از ۱۰۰۰ است. همچنین با فرض افزایش تعداد بازی‌ها انتظار داریم که تعداد گل‌ها نیز افزایش یابد که شرط سوم برای توزیع پواسون، در این تعریف نیز نادیده گرفته می‌شود.

با این توضیحات مشخص می‌شود که متغیر تصادفی که به صورت تعداد گل‌ها در سال در نظر گرفته شده است، نمی‌تواند به عنوان متغیر تصادفی پواسون در نظر گرفته شود. حال به بررسی تعریف دوم متغیر تصادفی می‌پردازیم و هماهنگی آن را با توزیع پواسون بررسی می‌کنیم.

II- با فرض X تعداد کل گل‌ها در یک بازه یک روزه

این بار تعریف جدید که براساس تعداد گل‌های زده شده در یک روز شکل گرفته است می‌خواهیم توزیع پواسون را برای متغیر تصادفی X بررسی کنیم. به کمک کدهای زیر، نمودارهای ارتباط تعداد بازی‌ها با تعداد گل‌ها در یک روز را رسم می‌کنیم. انتظار داریم که این نرخ برای روز‌های مختلف ثابت باشد.

1results %>% 
2  group_by(date) %>% 
3  summarise(numGoals = sum(totalGoals), numMatches = n()) %>% 
4  ggplot(aes(x = numMatches, y = numGoals)) + 
5  geom_point(color = "green") +
6  geom_smooth(se=FALSE) + 
7  labs(x = "تعداد مسابقات در روز",
8       y = "تعداد گل های زده شده در هر روز",
9       title = "مقایسه تعداد بازی در مقابل تعداد گل زده",
10       caption = "Data Source: https://www.kaggle.com/martj42/international-football-results-from-1872-to-2017") + 
11  theme(panel.background = element_blank(),
12        panel.grid.minor = element_line(colour = "grey"))

خروجی به صورت نمودار زیر خواهد بود. محور افقی در این نمودار تعداد مسابقات در هر روز و محور عمودی تعداد گل‌های زده شده در هر روز را نشان می‌دهد. مشخص است که براین اساس گاهی تعداد مسابقات ثبت شده در هر روز بیش از عدد ۶۰ است. به این ترتیب با توجه به زیاد بودن تعداد مسابقات انتظار داریم تعداد گل‌های زده نیز افزایش یابد.

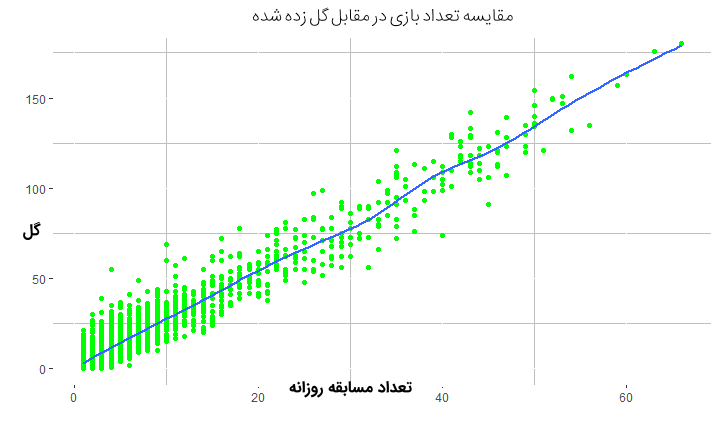
همینطور توسط کد زیر تعداد کل گل‌ها را براساس سال رسم کرده‌ایم. مشخص است که با افزایش سال (تکرارهای آزمایش) تعداد گل‌ها نیز افزایش داشته است، زیرا تعداد مسابقات نیز در هر روز افزایش نشان می‌دهد.

1results %>% 
2  group_by(date) %>% 
3  summarise(numGoals = sum(totalGoals)) %>% 
4  ggplot(aes(x=date, y=numGoals)) + 
5  geom_col(fill = "blue") +
6  labs(x = "روز", 
7       y = "کل گل های زده شده",
8       title = "تعداد کل گل های زده شده در هر روز",
9       caption = "Data Source: https://www.kaggle.com/martj42/international-football-results-from-1872-to-2017") + 
10  theme(panel.background = element_blank(),
11        panel.grid.minor = element_line(colour = "grey"),
12        axis.text.x=element_blank(),
13        axis.ticks.x=element_blank())

خروجی به صورت یک نمودار ستونی است که تعداد گل‌های زده شده در هر تاریخ را نشان می‌دهد. البته به یاد دارید که تعداد روز‌ها در اینجا بیش از ۳۸۰۰ است.

بنابراین تعداد موفقیت‌ها (گل‌ها) نسبت به تعداد آزمایش‌ها (مسابقات) کم است و شرط چهارم برقرار است ولی نرخ رخداد پیشامد ثابت نیست و به تعداد بازی بستگی دارد. در نتیجه تعریف دومی که برای متغیر تصادفی ایجاد کردیم باز هم با تعریف متغیر تصادفی و توزیع پواسون مطابقت ندارد.

III- با فرض X تعداد کل گل‌ها در یک مسابقه است

محاسبات و نمودارهای قبلی را برای این حالت نیز انجام می‌دهیم.

1results %>% 
2  ggplot(aes(totalGoals)) + 
3  geom_histogram(fill = "blue", binwidth = 1) +
4  labs(x = "دسته (طول=1)",
5       y = "گل های زده شده در هر مسابقه",
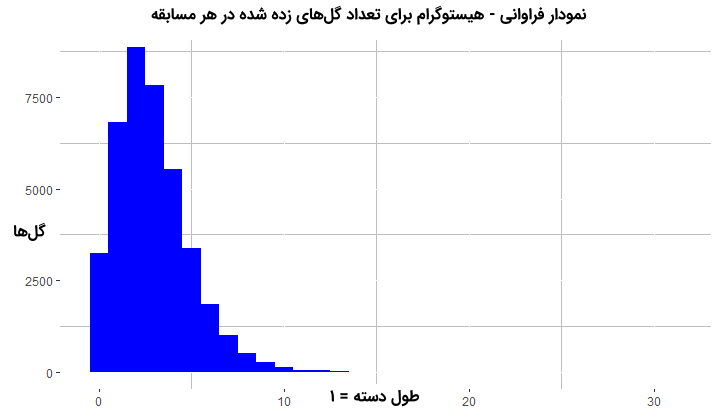
6       title = "نمودار فراوانی - هیستوگرام برای تعداد گل های زده شده در هر مسابقه",
7       caption = "Data Source: https://www.kaggle.com/martj42/international-football-results-from-1872-to-2017") + 
8  theme(panel.background = element_blank(),
9        panel.grid.minor = element_line(colour = "grey"))

با توجه به نمودار زیر مشخص می‌شود که متوسط تعداد گل‌های زده شده در هر مسابقه تقریبا ثابت است. در حقیقت میانگین برابر با 2.935642 گل در هر بازی است. از طرف دیگر به ثمر رسیدن یک گل وابسته به گل‌های دیگر نیست و به تعداد مسابقات نیز بستگی ندارد. همچنین تعداد مسابقات (تعداد آزمایش‌ها) بسیار بیشتر از تعداد گل‌ها در هر روز (تعداد موفقیت‌ها) است. پس به نظر می‌رسد که متغیر تصادفی معرفی شده می‌تواند دارای توزیع پواسون باشد.

محاسبه احتمال برای پیشامدهای توزیع پواسون

حال فرض کنید که می‌خواهیم برای متغیر تصادفی X که دارای توزیع پواسون است، مقدار احتمال برای رخداد k پیشامد در یک فاصله زمانی یا مکانی را محاسبه کنیم.

فیلم آموزش مبانی احتمالات (رایگان) در فرادرس

کلیک کنید

تابع احتمال توزیع پواسون به صورت زیر نوشته می‌شود.

$$P(X=k)=e^{-\lambda}\dfrac{\lambda ^k}{k!}$$

بطوری که $$\lambda$$ متوسط تعداد پیشامدها در یک فاصله است که در این جا همان متوسط گل در هر بازی محسوب می‌شود. از طرفی $$k$$‌ نیز تعداد گل‌هایی در روز است که می‌خواهیم احتمال را برایش محاسبه کنیم. با توجه به خصوصیات متغیر تصادفی که در حالت سوم تعریف کردیم، مشخص است که مقدار $$\lambda=2.935642$$ است. با این حساب مقدار احتمال زیر را می‌توان محاسبه کرد.

$$P(X=5)=e^{(-2.935642)}\times \dfrac{(2.935642)^5}{5!}=0.09647195841$$

این مقدار نشان می‌دهد، احتمال اینکه در یک بازی ۵ گل زده شود حدود ۱۰٪ است. حال با استفاده از دستور R‌ این محاسبه را انجام می‌دهیم.

1dpois(x = 5, lambda = mean(results$totalGoals))

پس از اجرای این فرمان مقدار 0.09647199 ظاهر خواهد شد که به مقدار محاسبه قبلی بسیار نزدیک است. برای نمایش نموداری که مقدارهای مختلف احتمال را برای تعداد گل‌های مختلف رسم می‌کند از کدی استفاده می‌کنیم که در ادامه دیده می‌شود. این نمودار همان شکل تابع احتمال توزیع پواسون است که با توجه به برآورد $$\lambda$$ توسط داده‌ها رسم شده است.

1tibble(x=0:8, px=dpois(0:8, lambda = mean(results$totalGoals))) %>% 
2  ggplot(aes(x=x, y=px)) + 
3  geom_smooth(se=FALSE) +
4  coord_cartesian(xlim = c(0,8)) +
5  labs(x = "تعداد گل ها"
6       , y= "احتمال",
7       title = "احتمال تعداد گل های زده در یک مسابقه",
8       caption = "Data Source: https://www.kaggle.com/martj42/international-football-results-from-1872-to-2017") + 
9  theme(panel.background = element_blank(),
10        panel.grid.minor = element_line(colour = "grey"))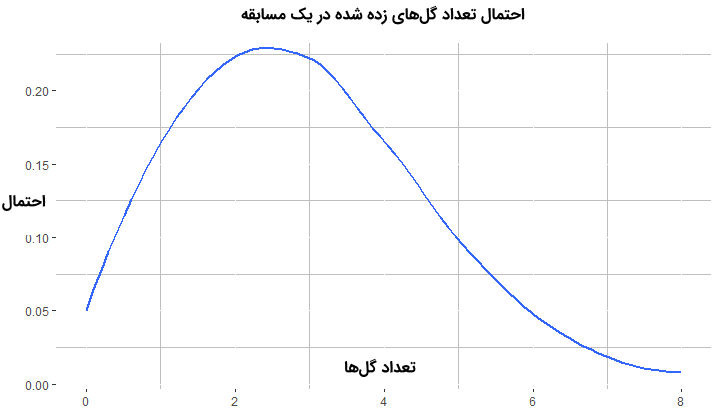

خلاصه

توزیع پواسون در صنعت کاربردهای زیادی دارد. بخصوص در نظریه صف و بهینه‌سازی منابع از آن استفاده می‌شود. برای مثال محاسبه احتمال اینکه تعداد k مشتری در فروشگاه جلوی صندوق فروش قرار گرفته باشند برمبنای توزیع پواسون انجام می‌شود. این کار باعث می‌شود منابع و تعداد فروشندگان را بهنیه انتخاب کرد. یا برای محاسبه احتمال ظاهر شدن یک صفحه وب با k بار به روز رسانی در موتورهای جستجو، از توزیع پواسون باید استفاده شود.

شایان ذکر است که فایل مربوط به همه کدهایی که در این متن به آن‌ها اشاره شده است را می‌توانید از طریق این لینک دریافت کنید.

اگر مطلب بالا برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش های برنامه نویسی متلب برای علوم و مهندسی
• متغیر های تصادفی – میانگین، واریانس و انحراف معیار – به زبان ساده
• آموزش آمار و احتمال مهندسی
• متغیر تصادفی، تابع احتمال و تابع توزیع احتمال
• آزمایش تصادفی، پیشامد و تابع احتمال
• متغیر تصادفی و توزیع دو جمله‌ای — به زبان ساده
• متغیر تصادفی و توزیع برنولی — به زبان ساده

^^