فرادرس
تغییر متغیر در انتگرال سه گانه — به زبان ساده (+ دانلود فیلم آموزش رایگان)
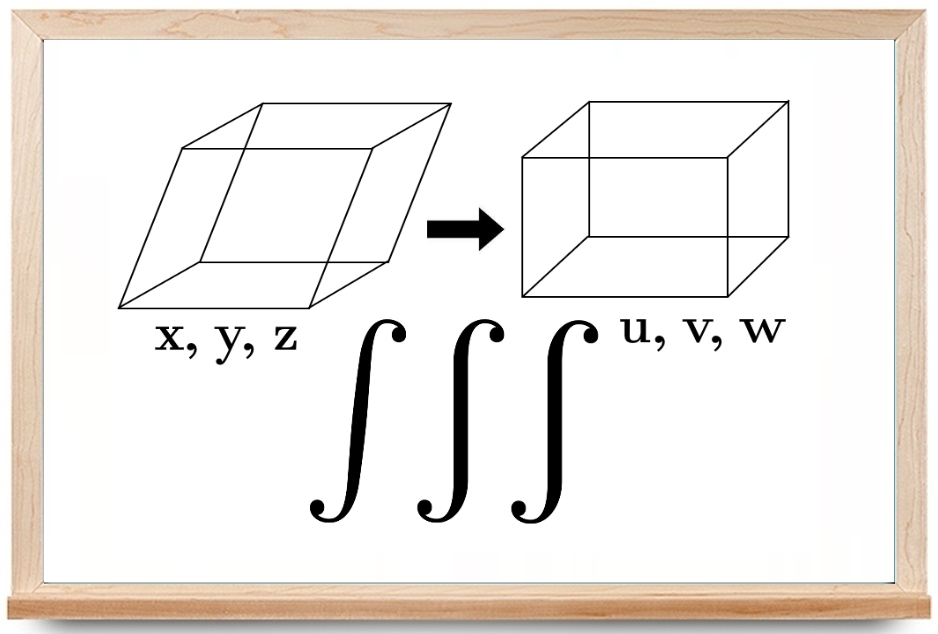
در آموزش‌های قبلی مجله فرادرس، درباره انتگرال و روش‌های محاسبه آن بحث کردیم. در این آموزش‌ها، مباحثی مانند انتگرال توابع مثلثاتی، انتگرال‌گیری جزء به جزء، انتگرال دوگانه و انتگرال سه‌گانه را معرفی کردیم. همچنین با تغییر متغیر و کاربرد آن در انتگرال‌گیری آشنا شدیم. در این آموزش، روش محاسبه انتگرال سه‌گانه را با کمک تغییر متغیر بیان می‌کنیم. با استفاده از تغییر متغیر در انتگرال سه گانه می‌توان ناحیه‌های انتگرال‌گیری را ساده کرده و انتگرال سه‌گانه را به ضرب سه انتگرال ساده تبدیل کرد.
تغییر متغیر در انتگرال سه گانه
انتگرال سه‌گانه زیر را در نظر بگیرید که در مختصات دکارتی $$x$$، $$y$$ و $$z$$ در ناحیه $$U$$ بیان شده است:
$$ \large \iiint\limits _ U { f \left( { x , y , z } \right) d xd y dz } . $$
می‌خواهیم انتگرال را در مختصات جدید $$u$$، $$v$$ و $$w$$ محاسبه کنیم. فرض می‌کنیم رابطه بین مختصات قدیم و جدید به‌صورت زیر باشد:
$$ \large { x = \varphi \left( { u , v , w } \right),\;\;}\kern-0.3pt
{ y = \psi \left( { u , v , w } \right),\;\;}\kern-0.3pt
{ z = \chi \left( { u , v , w } \right) . } $$
همچنین فرض می‌کنیم:
- توابع $$ \varphi $$، $$ \psi $$ و $$ \chi $$ نسبت به مشتقات جزئی‌شان پیوسته هستند.
- یک رابطه تک‌مقداری بین نقاط ناحیه انتگرال‌گیری $$U$$ در فضای $$xyz$$ و نقاط ناحیه $$ U^ \prime $$ در فضای $$uvw$$ وجود دارد.
- تبدیل ژاکوبین $$ I (u, v , w ) $$ که برابر است با:
$$ \large { I \left( { u , v , w } \right) } = { \frac{{\partial \left( { x , y , z } \right) } } { { \partial \left( { u , v , w } \right) } } }
= { \left| { \begin {array} { * { 20} { c } }
{\frac { { \partial x } } { { \partial u } } } & { \frac{{\partial x } } { { \partial v } } } & { \frac { { \partial x } } { { \partial w } } } \\
{\frac { { \partial y } } { { \partial u } } } & { \frac { { \partial y } } { { \partial v } } } & {\frac { { \partial y } } { {\partial w}}}\\
{\frac{{\partial z } } { { \partial u} } } & { \frac{{\partial z } } { { \partial v } } } & { \frac{{\partial z}}{{\partial w}}}
\end{array}} \right|} $$
غیرصفر بوده و علامت آن در هر نقطه‌ای از ناحیه انتگرال‌گیری $$U$$ تغییر نمی‌کند.
آن‌گاه، فرمول تغییر متغیر انتگرال سه‌گانه به‌صورت زیر خواهد بود:
$$ \large { \iiint \limits _ U { f \left( { x , y, z } \right) d xd yd z } \text { = } } \kern-0.3pt
{ \iiint \limits _ { U ’ } { f \left( { \varphi,\psi,\chi} \right) \cdot} \kern0pt{\left|{I\left( { u , v , w } \right)} \right| d ud v dw } .} $$
همچنین، $$ \varphi $$، $$ \psi $$ و $$ \chi $$ توابعی از متغیرهای $$x$$، $$y$$ و $$z$$ هستند و $$ \left| {I\left( {u,v,w} \right)} \right| $$ قدر مطلق ژاکوبین است.
اغلب ساده‌تر است که انتگرال‌های سه‌گانه را در مختصات استوانه‌ای یا کروی محاسبه کنیم.
مثال‌ها
در ادامه، دو مثال از روش تغییر متغیر در انتگرال سه‌گانه را بررسی می‌کنیم.
مثال ۱
حجم ناحیه $$U$$ را که به‌صورت زیر تعریف شده است، بیابید:
$$ \large { 0 \le z \le 2,\;\;\;}\kern0pt
{0 \le y + z \le 5,\;\;\;}\kern0pt
{0 \le x + y + z \le 10.} $$
حل: واضح است که این ناحیه، یک متوازی‌السطوح را نشان می‌دهد. اگر به‌گونه‌ای از تغییر متغیر استفاده کنیم که ناحیه مورد نظر به یک مکعب مستطیل تبدیل شود، انتگرال سه‌گانه را می‌توان به ضرب سه انتگرال ساده تبدیل کرد.
بنابراین، از تغییر متغیرهای زیر استفاده می‌کنیم:
$$ \large { u = x + y + z,\;\;\;}\kern-0.3pt
{ v = y + z,\;\;\;}\kern-0.3pt
{ w = z . } $$
ناحیه انتگرال‌گیری $$ U’ $$ با متغیرهای جدید $$u$$، $$v$$ و $$w$$ با نامعادله‌های زیر تعریف می‌شود:
$$ \large {0 \le u \le 10,\;\;\;}\kern0pt
{0 \le v \le 5,\;\;\;}\kern0pt
{0 \le w \le 2 . } $$
در نتیجه، حجم مورد نظر را می‌توان با انتگرال زیر به‌دست آورد:
$$ \large { V = \iiint\limits _ U { d x d y d z } }
= {\iiint \limits _ { U ’ } { \left| { I \left( { u , v , w } \right)} \right|dudvdw} .} $$
در ادامه، ژاکوبین این تبدیل را محاسبه می‌کنیم. برای آنکه متغیرهای قدیمی $$x$$، $$y$$ و $$z$$ در متغیرهای جدید $$ u$$، $$v$$ و $$w$$ نباشند، ابتدا ژاکوبین تبدیل معکوس را به‌دست می‌آوریم:
$$ \large { \frac { { \partial \left( { u , v , w } \right) } } { {\partial \left( {x , y , z} \right) }} }
= {\left| {\begin{array} { * { 20 } { c }}
{\frac{{\partial u } } { { \partial x } } } & { \frac{{\partial u } } { { \partial y } } } & { \frac { { \partial u } } { { \partial z } } }\\
{\frac { { \partial v } } { { \partial x } } } & { \frac { { \partial v } } { { \partial y } } } & { \frac { { \partial v } } { { \partial z } } } \\
{\frac{{\partial w } } { { \partial x } } } & { \frac{{\partial w}}{{\partial y}}}&{\frac{{\partial w}}{{\partial z}}}
\end{array}} \right| }
= { \left| {\begin{array}{*{20}{c}}
1 & 1 & 1 \\
0 & 1 & 1 \\
0 & 0 & 1
\end {array} } \right| }
= {1 \cdot \left| {\begin{array} { * { 2 0 } { c} }
1 & 1\\
0 & 1
\end{array}} \right| }
={ 1 – 0 = 1.} $$
در نتیجه، داریم:
$$ \large { \left| { I \left( { u , v , w } \right)} \right| }
= {\left| {\frac{{\partial \left( {x , y , z } \right)}}{{\partial \left( { u , v , w } \right)}}} \right| }
= { \left| { { { \left( { \frac{{\partial \left( { u , v , w } \right)}}{{\partial \left( { x , y , z } \right)}}} \right) } ^ { – 1 } } } \right| } = { 1 . } $$
بنابراین، حجم مورد نظر برابر است با:
$$ \large {V }={ \iiint\limits_{U’} {\left| {I\left( {u,v,w} \right)} \right|d u d vdw} }
= {\iiint\limits_{U’} {dudvdw} } \\ \large
= {\int\limits _ 0 ^ { 10} { d u } \int\limits_0^5 {dv} \int\limits _ 0 ^ 2 {dw} }
= {10 \cdot 5 \cdot 2 }={ 100.} $$
مثال ۲
حجم متوازی‌السطوحی با نامعادلات زیر را بیابید:
$$ \large {0 \le 2x – 3y + z \le 5,\;\;\;}\kern0pt
{1 \le x + 2y \le 4,\;\;\;}\kern0pt
{ – 3 \le x – z \le 6.} $$
حل: متغیرهای جدید زیر را تعریف می‌کنیم:
$$ \large {u = 2x – 3y + z,\;\;\;}\kern0pt
{v = x + 2y,\;\;\;}\kern0pt
{w = x – z.} $$
در ادامه، ژاکوبین تبدیل معکوس را محاسبه می‌کنیم:
$$ \large {\frac{{\partial \left( {u,v,w} \right)}}{{\partial \left( {x,y,z} \right)}} }
= {\left| {\begin{array}{*{20}{c}}
{\frac{{\partial u}}{{\partial x}}}&{\frac{{\partial u}}{{\partial y}}}&{\frac{{\partial u}}{{\partial z}}}\\
{\frac{{\partial v}}{{\partial x}}}&{\frac{{\partial v}}{{\partial y}}}&{\frac{{\partial v}}{{\partial z}}}\\
{\frac{{\partial w}}{{\partial x}}}&{\frac{{\partial w}}{{\partial y}}}&{\frac{{\partial w}}{{\partial z}}}
\end{array}} \right| }
= {\left| {\begin{array}{*{20}{c}}
2&{ – 3}&1\\
1&2&0\\
1&0&{ – 1}
\end{array}} \right|.} $$
دترمینان را می‌توان به‌صورت زیر محاسبه کرد:
$$ \large {\frac{{\partial \left( {u,v,w} \right)}}{{\partial \left( {x,y,z} \right)}} }
= {\left| {\begin{array}{*{20}{c}}
2&{ – 3}&1\\
1&2&0\\
1&0&{ – 1}
\end{array}} \right| } \\ \large
= {1 \cdot \left| {\begin{array}{*{20}{c}}
{ – 3}&1\\
2&0
\end{array}} \right| – 1 \cdot \left| {\begin{array}{*{20}{c}}
2&{ – 3}\\
1&2
\end{array}} \right| }
= { – 2 – 7 }={ – 9.} $$
قدر مطلق ژاکوبین تبیدل مستقیم، برابر است با:
$$ \large {\left| {I\left( {u,v,w} \right)} \right| }
= {\left| {\frac{{\partial \left( {x,y,z} \right)}}{{\partial \left( {u,v,w} \right)}}} \right| }
= {\left| {{{\left( {\frac{{\partial \left( {u,v,w} \right)}}{{\partial \left( {x,y,z} \right)}}} \right)}^{ – 1}}} \right| }
= {\left| {\frac{1}{{ – 9}}} \right| }={ \frac{1}{9}.} $$
اکنون به‌سادگی می‌توان حجم مورد نظر را محاسبه کرد:
$$ \large {V }={ \iiint\limits_{U’} {\left| {I\left( {u,v,w} \right)} \right|dudvdw} }
= {\iiint\limits_{U’} {\frac{1}{9}dudvdw} } \\ \large
= {\frac{1}{9}\int\limits_0^5 {du} \int\limits_1^4 {dv} \int\limits_{ – 3}^6 {dw} }
= {\frac{1}{9} \cdot 5 \cdot 3 \cdot 9 }={ 15.} $$
اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:
^^
فیلم های آموزش تغییر متغیر در انتگرال سه گانه — به زبان ساده (+ دانلود فیلم آموزش رایگان)
فیلم آموزشی تغییر متغیر در انتگرال سه‌گانه
فیلم آموزشی تغییر مختصات استوانه‌ای در انتگرال سه‌گانه
فیلم آموزشی تغییر مختصات کروی در انتگرال سه‌گانه
