تغییر متغیر — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

در مطالب قبلی وبلاگ فرادرس به صورت دقیق مفهوم توابع مختلف و دامنه و برد آن‌ها مورد ارزیابی قرار گرفت. همانطور که در این مطالب اشاره شد، یکی از موارد بسیار مهم در علم ریاضیات، تغییر متغیر است که به کمک آن می‌توان معادلات مختلف را به سادگی حل کرد. کاربرد دیگر روش تغییر متغیر در بیان ساده توابع و محاسبه سریع دامنه و برد آن‌ها است. همچنین به کمک تغییر متغیر می‌توان محاسبه مشتق و انتگرال توابع پیچیده را به راحتی مورد بررسی قرار داد.

این مطلب به صورت دقیق به بررسی شیوه استفاده از روش تغییر متغیر برای حل معادلات مختلف می‌پردازد. بنابراین در صورتی که معادله مورد نظر ما قابل حل نباشد، ابتدا تغییر متغیر را بر آن اعمال و در فضای جدید، معادله را حل می‌کنیم و در نهایت حل نهایی را دوباره به حالت اولیه قبل از تغییر متغیر، باز می‌گردانیم.

ایده اصلی حل معادلات به کمک روش تغییر متغیر در شکل زیر نشان داده شده است.

بنابراین طبق توضیحات ارائه شده و شکل بالا، می‌توان روند کلی حل معادلات به کمک روش تغییر متغیر را با سه مرحله زیر بیان کرد.

• مرحله اول این است که عبارت دلخواه و مناسبی را در معادله مانند «2x-3» با متغیر جدید مانند «U» تعویض کنیم.
• مرحله دوم، شامل حل معادله جدیدی می‌شود که در مرحله اول بر حسب U نوشته شده است.
• مرحله سوم این است که عبارت تغییر متغیر موجود در مرحله اول (در اینجا «2x-3») را در پاسخ مرحله دوم قرار دهیم (در مثال ذکر شده 2x-3 را برابر با U قرار می‌دهیم).

فیلم آموزش حسابان ۱ – پایه یازدهم – حل تمرین در فرادرس

کلیک کنید

در ادامه، مراحل توضیح داده شده در بالا را با استفاده از چند مثال به صورت دقیق مورد مطالعه قرار می‌دهیم.

مثال 1

پاسخ معادله درجه دو نشان داده شده در رابطه زیر را با استفاده از روش تغییر متغیر محاسبه کنید.

$$(x+1)^2 -4 =0$$

برای حل این رابطه به کمک روش تغییر متغیر، همانطور که در بخش قبل توضیح داده شد، سه مرحله را باید طی کنیم. مرحله اول این است که برای ساده سازی معادله، عبارتی را با استفاده متغیر جدید تعویض کنیم.

بنابراین در این مثال برای ساده سازی معادله، عبارت x+1 را با حرف U تعویض می‌کنیم. بر این اساس معادله به فرم ساده شده زیر در می‌آید.

$$(U)^2 -4 =0$$

حال در مرحله دوم، پاسخ معادله بالا را محاسبه می‌کنیم. همانطور که می‌دانید پاسخ معادله بالا برابر با $$U = \pm 2$$ است.

در مرحله سوم عبارت تغییر متغیر استفاده شده در مرحله اول را به حالت اول باز می‌گردانیم. بنابراین به جای U عبارت x+1 را قرار می‌دهیم. بنابراین داریم:

$$x+1 = \pm 2$$

در نهایت واضح است که حاصل عبارت فوق برابر با x=1 یا x=-3 می‌شود. بنابراین معادله درجه دو نشان داده شده در این مثال پاسخی برابر با 1 یا 3- دارد. روندی که در بالا و در سه مرحله به صورت دقیق توضیح داده شد را می‌توان با استفاده از روابط شکل زیر نیز به صورت خلاصه بیان کرد.

نکته دیگری که در مبحث تغییر متغیر باید به آن توجه کرد، موضوع بررسی و چک کردن پاسخ نهایی است. در واقع در این مرحله باید درستی پاسخ نهایی از طریق جایگذاری در معادله اولیه، مورد ارزیابی قرار بگیرد. این موضوع در مثال‌های زیر به صورت دقیق مورد مطالعه قرار می‌گیرد.

مثال 2

معادله درجه دو زیر را در نظر بگیرید.

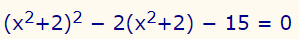
پاسخ این معادله را با استفاده از روش تغییر متغیر محاسبه کنید.

فیلم آموزش ریاضی 2 – پایه یازدهم علوم تجربی در فرادرس

کلیک کنید

با دقت به معادله بالا متوجه می‌شوید که حل این معادله به شیوه مستقیم بسیار سخت و پیچیده است. بنابراین برای محاسبه آن نیاز به استفاده از روش تغییر متغیر داریم.

بر این اساس در گام نخست برای حل این معادله به روش تغییر متغیر، عبارت $$x ^ 2 + 2$$ را برابر با متغیر U قرار می‌دهیم و تغییر متغیر را بر این معادله اعمال می‌کنیم. با اعمال این تغییر متغیر، معادله فوق به شکل زیر در می‌آید.

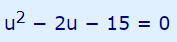
حال در گام دوم نیاز به حل معادله فوق داریم. بنابراین همانطور که مشاهده می‌شود، این معادله که یک معادله درجه دو است و می‌توان آن را به راحتی به صورت حاصل ضرب دو عبارت مختلف به شکل زیر بیان کرد.

$$(U-5) (U+3)=0$$

بنابراین پاسخ معادله فوق برابر با $$U=5$$ یا $$U=-3$$ خواهد بود. در ادامه و برای رسیدن به پاسخ نهایی، باید متغیر U را با عبارتی که در گام اول به عنوان تغییر متغیر در نظر گرفته شد، جایگزین کرد. بنابراین مقدار U را برابر با $$x ^ 2 + 2$$ قرار می‌دهیم. از آنجایی که U دو مقدار 5 و 3- را در بر می‌گیرد، پاسخ این مسئله به شکل زیر در می‌آید.

در حالت اول که U=5 است داریم:

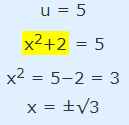
در حالت دوم که U=-3 است نیز می‌توان محاسبات را به شکل زیر ادامه داد.

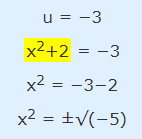
همانطور که مشاهده می‌شود عبارت زیر رادیکال برابر با مقداری منفی است و با توجه به آنکه جذر عبارت منفی پاسخ حقیقی ندارد، پاسخ معادله بالا به صورت مختلط به دست می‌آید که قابل قبول نیست. بنابراین پاسخ نهایی مسئله تنها عبارت اول (پاسخ U=5) را شامل می‌شود که در رابطه زیر نشان داده شده است.

در ادامه نیاز هست که دو پاسخ فوق را در معادله اصلی مسئله جایگذاری کنیم و درستی پاسخ به دست آمده را مورد ارزیابی و مطالعه قرار دهیم. این روند در ادامه به صورت دقیق بررسی شده است.

همانطور که مشاهده می‌شود، دو پاسخ فوق در معادله مسئله صدق می‌کنند. بنابراین پاسخ نهایی این معادله برابر با دو عدد زیر است.

مثال 3

معادله‌ای که در رابطه زیر نشان داده شده را در نظر بگیرید.

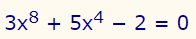
با استفاده از روش تغییر متغیر، این معادله را حل کنید.

فیلم آموزش ریاضی و آمار 2 – پایه یازدهم علوم انسانی در فرادرس

کلیک کنید

با دقت به رابطه بالا متوجه می‌شوید که با یک معادله درجه ۸ روبه‌رو هستیم و حل این معادله به شیوه مستقیم غیر ممکن است. بنابراین از روش تغییر متغیر برای حل آن استفاده می‌کنیم. این تغییر متغیر در رابطه زیر نشان داده شده است.

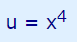
با قرار دادن تغییر متغیر بالا در معادله ابتدای این مثال، معادله به شکل ساده شده زیر در می‌آید.

حال معادله بالا که یک معادله درجه دو است را می‌توان به راحتی محاسبه کرد و پاسخ‌های آن را به دست آورد. بنابراین پاسخ معادله بالا به شکل زیر خواهد بود.

همانطور که مشاهده می‌شود، مسئله حاضر، دو پاسخ دارد که یکی از آن‌ها مثبت و دیگری منفی است. گام بعدی این است که u در دو پاسخ بالا را برابر با $$u = x^4$$ قرار دهیم و مقدار x که پاسخ نهایی مسئله است را محاسبه کنیم. برای پاسخ اول یعنی $$u = {1 \over 3}$$ داریم:

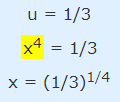
مقدار x را در پاسخ دوم u یعنی $$u = -2$$ به شکل زیر محاسبه می‌کنیم.

بر این اساس در صورتی که حقیقی و یا مختلط بودن پاسخ برای ما مهم نباشد، مسئله مورد نظر دو پاسخ زیر را در بر می‌گیرد.

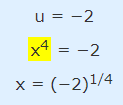
بنابراین همانطور که اشاره شد برای حل یک مسئله به کمک روش تغییر متغیر سه مرحله باید طی شود. مرحله اول این است که یک ترم در معادله را با متغیر دلخواه U تعویض کنیم. در مرحله دوم معادله جدید که نتیجه اعمال تغییر متغیر بر معادله اول است را حل می‌کنیم و در مرحله سوم عبارت تغییر متغیر که در گام اول اعمال شد را به جای U قرار می‌دهیم و پاسخ نهایی مسئله را محاسبه می‌کنیم.

در صورتی که به مباحث مرتبط در زمینه ریاضیات پایه علاقه‌مند هستید، آموز‌ش‌های زیر به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• مجموعه آموزش‌های ریاضی و فیزیک
• مجموعه آموزش‌های دروس رسمی دبیرستان و پیش دانشگاهی
• اعداد گویا — به زبان ساده
• قدر مطلق (Absolute Value) — به زبان ساده
• اعداد مختلط – به زبان ساده
• مفاهیم تابع – به زبان ساده

^^