آزمون KMO و بارتلت در تحلیل عاملی | معیارهای کفایت حجم نمونه

در بررسی و تحقیقاتی که برمبنای تحلیل عاملی اکتشافی (EFA)، تعیین حجم نمونه و وجود همبستگی مناسب بین متغیرها از اهمیت ویژه‌ای برخودار است. دو آزمون KMO و بارتلت در تحلیل عاملی به محققین این امکان را می‌دهند که قبل از اجرای تحلیل عاملی اکتشافی از بسندگی یا کفایت حجم نمونه و وجود کرویت در متغیرها مطمئن شده، سپس تحلیل عاملی را به کار برند. نرم‌افزارهای مختلفی نیز برای مشخص کردن شاخص‌ها و اجرای آزمون‌های مربوط به تحلیل عاملی وجود دارد که در این بین می‌توان به نرم‌افزار SPSS نیز اشاره کرد. در نوشتارهای دیگر مجله فرادرس که در ادامه معرفی شده‌اند، به بررسی مثال‌هایی برای بدست آوردن و اجرای آزمون KMO و بارتلت در تحلیل عاملی پرداخته‌ایم ولی نوشتار جاری، به مفهوم و نحوه محاسبه این معیارها در آزمون KMO و بارتلت در تحلیل عاملی می‌پردازد.

بهتر است به عنوان مقدمه و آشنایی با تحلیل عاملی و انواع آن،‌ مطالب متغیر پنهان در مدل‌ ساختاری — به زبان ساده و مدل معادلات ساختاری (Structural Equation Modeling) — مفاهیم، روش‌ها و کاربردها را مطالعه کنید. همچنین خواندن نوشتارهای تحلیل عاملی با SPSS — راهنمای گام به گام و کاربردی و معادلات برآوردیابی تعمیم یافته (GEE) در آمار | به زبان ساده نیز خالی از لطف نیست.

آزمون KMO و بارتلت در تحلیل عاملی

می‌دانید که رویکرد «تحلیل عاملی اکتشافی» (Exploratory Factor Analysis) در تحلیل عاملی، زمانی به کار می‌رود که از مدل و ارتباط بین متغیرها هیچ اطلاعی نداریم و قرار است با تکیه بر داده‌ها دست به تولید یا ایجاد یک مدل ارتباطی بزنیم. در این حالت، از تحلیل عاملی اکتشافی کمک گرفته و با توجه به ساختار ماتریس همبستگی یا کوواریانس، مدلی را پیشنهاد می‌دهیم. به همین علت به چنین وضعیتی تحلیل اکتشافی می‌گویند. ساده‌ترین توضیح ممکن در مورد نحوه کار در این تکنیک آن است که سعی به ایجاد گروهی از متغیرها داریم که بسیار به هم مرتبط هستند و هر دسته یا گروه با بقیه متغیرها، وابستگی کمی دارد.

اما اگر در نمونه‌گیری و تعیین حداقل حجم مورد نیاز برای استفاده از EFA دچار مشکل باشیم، چگونه عمل خواهیم کرد. این امر به این معنی است که استفاده از قضیه حد مرکزی برای توجیه نرمال بودن توزیع داده‌ها و همچنین محاسبه و تفکیک ماتریس کوواریانس بدون دانستن ساختار ماتریس واریانس-کوواریانس در بین گروه‌ها ممکن است با شکست مواجه شود. هر دو روش یعنی آزمون KMO و بارتلت در تحلیل عاملی راه‌کارهایی برای تشخیص چنین وضعیتی را ارائه می‌کنند. به همین علت، قبل از تحلیل EFA بهتر است به وسیله این معیارها، نسبت به شرایط اولیه EFA کسب اطلاع کرده، سپس تحلیل عاملی اکتشافی را به کار گیریم.

در ادامه نحوه محاسبه هر دو آماره‌ها و آزمون KMO و بارتلت در تحلیل عاملی و محدوده‌های قابل قبول برای آن‌ها را بازگو خواهیم کرد.

آماره و آزمون بارتلت

در آمار، از آزمون بارتلت، که به افتخار مبدع آن «موریس استیونسون بارتلت» (Maurice Stevenson Bartlett) آمارشناسی انگلیسی نام‌گذاری شده است، برای آزمایش همسانی یا «همسنگی واریانس‌ها» (Homoscedasticity) استفاده می‌شود، یعنی اگر چندین نمونه از جمعیت‌ دارای واریانس برابر باشد، آن‌ها را همسنگ یا با یکدیگر، همگن می‌نامند.

نکته: به یاد دارید که واریانس و معیارهای پراکندگی، شاخصی برای نشان دادن پراکندگی و یا به شکل دیگر، همگنی داده‌ها و جوامع آماری هستند.

برخی از تست‌های آماری، مانند تجزیه و تحلیل، فرض می‌کنند که واریانس‌ها در گروه‌ها یا نمونه‌ها برابر هستند، که با آزمون بارتلت قابل تأیید است.

در آزمون بارتلت، محقق، خود فرضیه صفر و جایگزین را می‌سازد. برای این منظور چندین روش آزمون ابداع شده است. در این متن به روش آزمون مبتنی بر برآوردگر کمترین مربعات (MSE) برای تشکیل آماره و فرضیه‌های آزمون بارتلت اشاره خواهیم کرد.

به این ترتیب بر اساس آماره‌ای است که توزیع نمونه‌ای آن تقریباً یک «توزیع  کای ۲» (Chi-Square) با (k-1) درجه آزادی است بهره می‌بریم. بطوری که k نمایانگر تعداد نمونه‌های تصادفی است و ممکن است در هر نمونه اندازه‌ای متفاوت داشته باشد. از طرفی توزیع هر یک از جوامع نیز نرمال فرض شده و استقلال نیز در این حالت منظور گردیده است.

آزمون بارتلت نسبت به دور شدن توزیع جامعه از توزیع نرمال حساس است. یعنی اگر نمونه‌ها از جوامعی با توزیع‌های غیر نرمال بدست آمده باشند، آزمون بارتلت ممکن است به سادگی منحرف شده و نتایج نادرست ارائه کند.

نکته: در این حالت «آزمون لون» (Leven's Test) و «آزمون براون-فورسید» (Brown-Forsythe) گزینه‌هایی بهتری نسبت به آزمون بارتلت هستند که نسبت به خروج از توزیع نرمال حساسیت کمتری دارند.

در آزمون بارتلت که در ادامه متن به کار خواهیم برد، فرض صفر ($$H_0$$) براساس ثابت بودن واریانس k جامعه شکل می‌گیرد در حالیکه فرض مقابل ($$H_a$$) بیانگر آن است که حداقل دو جامعه دارای واریانس یکسان نیستند.

همانطور که می‌بینید، فرض صفر با همگنی و همسنگی همه جوامع از لحاظ واریانس دلالت دارد در حالیکه فرض مقابل این فرضیه را رد می‌کند. به این ترتیب اگر از k جامعه نمونه‌هایی به اندازه $$n_i$$ داشته باشیم و $$S_i^2$$ نشانگر واریانس جامعه $$i$$ام باشد، آنگاه آماره بارتلت به صورت زیر نوشته می‌شود.

$$\large {\displaystyle \chi ^{2} = {\dfrac {(N-k) \ln( S_{p }^{2} ) - \sum_{ i = 1}^{ k}( n_{i} -1) \ln( S_{i }^{ 2}) }{ 1 + {\dfrac {1}{ 3 (k - 1)}} \left( \sum_{i = 1}^{ k}({ \dfrac {1 }{ n_{i } - 1}} ) - {\dfrac {1}{ N - k }} \right)} }}$$

توجه داشته باشید که در این رابطه محدودیتی به صورت زیر باید در نظر گرفته شود.

$$\large N = \sum_{ i = 1 }^k n_i$$

واضح است که واریانس آمیخته نیز به شکل زیر محاسبه شده است.

$$\large {\displaystyle S_{ p}^{ 2} = { \dfrac {1}{N - k}} \sum_{ i}(n_{ i} - 1 ) S_{ i}^{ 2 }}$$

با توجه به این شکل آماره آزمون بارتلت که به صورت نسبت مربع دو توزیع نرمال استاندارد مشخص شده، به طور مجانبی، توزیع کای ۲ یا خی ۲ با k-1 درجه آزادی تحت فرض صفر خواهد بود. به این ترتیب اگر مقدار آماره از صدک $$\alpha$$ام چنین توزیعی بزرگتر باشد، فرض صفر را می‌کنیم.

$$\large \chi^2 > \chi^2_{ k - 1, \alpha}$$

منظور از $$\chi^2_{k-a,\alpha}$$‌ همان صدک بالایی توزیع کای ۲ با k-1‌ درجه آزادی است که ناحیه بحرانی را تشکیل داده است.

نکته: همانطور که می‌بینید، آماره آزمون بارتلت، نسبت به آزمون نسبت درستنمای دارای کمی تغییرات است تا آماره آن به صورت مجانبی دارای توزیع کای ۲ شود.

فیلم آموزش تجزیه و تحلیل اطلاعات با نرم افزار SAS ساس در فرادرس

کلیک کنید

البته گاهی به جای استفاده از لگاریتم طبیعی از لگاریتم مبنای ۱۰ نیز در رابطه بالا استفاده می‌شود که در این حالت آماره آزمون بارتلت را به شکل زیر بازنویسی می‌کنند.

$$\large {\displaystyle \chi ^{2} = 2.3026{ \dfrac {(N - k ) \log_{ 10 }( S_{ p }^{2 }) - \sum_{i = 1 }^{ k}( n_{ i} - 1 ) \log_{ 10}( S_{ i}^{ 2}) }{ 1 + {\dfrac {1}{3 (k - 1)} } \left( \sum_{ i = 1 }^{ k}({ \dfrac{1 }{ n_{i} - 1} }) - {\dfrac { 1}{ N - k} } \right)}}}$$

در ادامه به ذکر یک مثال و نحوه اجرا و تفسیر آزمون KMO و بارتلت در تحلیل عاملی خواهیم پرداخت.

آزمون KMO

«کایزر» مقیاس و شاخص کفایت نمونه (MSA) را در سال ۱۹۷۰ معرفی کرد که بعداً در سال ۱۹۷۴ توسط «کایزر» (Kaiser) و «رایس» (Raise) اصلاح شد. آماره KMO که در سال‌های بعد معرفی شد، این شاخص را به صورت استاندارد شده درآورده بطوری که مقدار آن در بازه 0 تا 1 تغییر می‌کند. بزرگ بودن این مقدار نشان دهنده قدرت یا بهبود درجه پیش بینی هر متغیر توسط سایر متغیرها است که در عین حال مجموع خطا آن نیز ناچیز است. مشخص است که نزدیکی این مقدار به عدد صفر نشانگر ضعیف بودن مدل پیش‌بینی بوده و امکان استفاده از EFA را توجیه نمی‌کند.

از طرفی، اندازه گیری کفایت نمونه‌گیری (MSA) نشان می‌دهد آیا شاخص یا متغیر خاصی باید در تجزیه و تحلیل عاملی لحاظ شود و در مقابل معیار Kaiser-Meyer-Olkin (همچنین KMK یا KMO) نشانگر آن است که آیا یک مجموعه داده برای تجزیه و تحلیل عاملی، بسنده و کافی است؟ اگر داده‌های چند متغیره دارای توزیع تقریبی نرمال چند بعدی باشند،، از آزمون کرویت بارتلت که در بالا به آن اشاره کردیم، مناسب خواهد بود و شرط استفاده از تحلیل عاملی را به کمک آن می‌توان مشخص کرد.

نکته: این آماره (KMO) و آزمون آن توسط سه دانشمند به نام‌های «کایزر» (Kaiser)، «میر» (Meyer) و «الکین» (Olkin) ابداع و بهبود یافته است.

اندازه گیری کفایت نمونه برداری برای هر شاخص به صورت زیر محاسبه می‌شود.

$$\large {\displaystyle MSA_{ j} = { \dfrac {\displaystyle \sum_{ k \neq j} r_{ j k} ^{2}} {\displaystyle \sum_ {k \ neq j} r_{ j k}^ { 2} + \sum_{k \neq j} p_{jk} ^ {2}}}}$$

از طرفی معیار کایزر-مایر-اولکین نیز فرمولی به صورت زیر دارد.

$$\large {\displaystyle K M O = {\dfrac {\displaystyle {\underset {j \ neq k} {\sum \sum}} r_{j k} ^ {2}} {\displaystyle {\underset {j \ neq k} {\sum \sum}} r_{ j k} ^ {2} + {\underset {j \ neq k} {\sum \sum}} p_{j k} ^ {2}}}}$$

1. اندازه یا شاخص KMO در حقیقت، کیفیت معرف‌ها یا متغیرهای آشکار را مشخص می‌کند و معیاری برای کافی بودن اندازه نمونه نیست. در مقابل MSA برای تعیین کفایت اندازه نمونه در تحلیل عاملی به کار می‌رود.
2. به یاد داشته باشید که محاسبه و به کارگیری شاخص KMO، فقط در تحلیل آماری عاملی اکتشافی است و هیچ جایگاهی در تحلیل آماری عاملی تأییدی ندارد. می‌دانید که هر دو روش اکتشافی و تاییدی، بخشی از تحلیل عاملی (Factor Analysis) محسوب می‌شوند.

معیار یا ضریب همبستگی ضد تصویر

یکی از شاخص‌های دیگر برای کفایت و مناسب بودن متغیرها در تحلیل عاملی، استفاده از «ماتریس معیار همبستگی ضد تصویر» (Anti-image Correlation Matrix) است که براساس شاخص‌های KMO و بارتلت محاسبه شده و به کار می‌رود.

در تجزیه و تحلیل عامل، ماتریس همبستگی ضد تصویر مبنایی برای بررسی آن است که آیا یک مجموعه داده دارای m شاخص (متغیرها) قابلیت استخراج عامل یا عامل‌ها را داراست یا خیر،. این امر می‌تواند توسط این ماتریس و عناصر قطر اصلی آن نشان داده شود.

ماتریس همبستگی ضد تصویر، شامل همبستگی‌های جزئی با مقادیر منفی خارج از قطر اصلی ماتریس$${\displaystyle p_{j k}}$$ بین دو شاخص است. این مقادیر نشان می‌دهند که اگر یکی از متغیر تحت تأثیر سایر متغیرها باشد، همبستگی بین دو شاخص یا متغیر چقدر است. اگر مجموعه داده‌ها با عوامل مشترک دنبال شوند و هر عامل، حداقل سه شاخص را به کار گیرد، همبستگی های جزئی باید نزدیک به صفر باشد.

نکته: اندازه کفایت نمونه، عناصر روی قطر اصلی ماتریس همبستگی ضد تصویر در SPSS هستند. در تصویری که برای مثال زیر آورده شده، ماتریس همبستگی ضد تصویر و درایه‌های قطر اصلی را مشاهده می‌کنید.

یک مثال عملی

در میکرو سرشماری سال 2002 بررسی شد که چند بار پاسخ دهندگان مجاز یا مجبور به کار در روزهای شنبه (EF147)، یکشنبه/تعطیلات رسمی (EF148)، کار در عصر (EF149)، کار در شب (EF150) ، ساعت شب (EF151)، شیفت کاری (EF152) یا کار در ایام تعطیلات عید (EF163) شده‌اند. متاسفانه دسترسی به این داده‌ها میسر نبوده و فقط نتایج حاصل از تحلیل را مشاهده می‌کنید.

برای این داده‌ها، معیار کایزر-مایر-اولکین (کادر قرمز اول) 0٫600 را نشان می دهد و بنابراین این هفت شاخص تقریباً مناسب برای تحلیل عاملی هستند. طبق آزمون صورت گرفته براساس آماره بارلت، مقدار 614674، معنی‌دار بوده و نمی‌توان آن را صفر در نظر گرفت. زیرا مقدار p-value تقریبا صفر و کوچکتر از احتمال خطای نوع اول (در اینجا ۰٫۰۵) است.

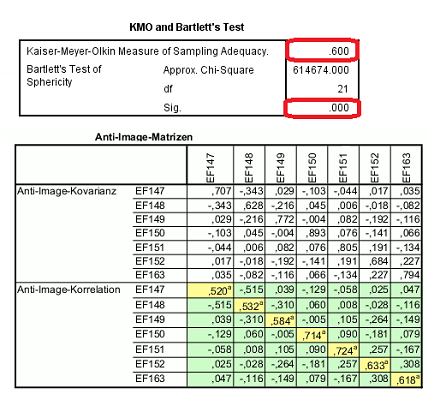
نکته: خروجی بالا مربوط به نرم‌افزار SPSS بوده که از طریق دستور تحلیل عاملی (Factor) از فهرست Dimension Reduction قابل دسترس است.

فیلم آموزش نرم‌ افزار لیزرل – مدل‌ سازی معادلات ساختاری SEM با LISREL – مقدماتی در فرادرس

کلیک کنید

جدول مربوط به تصویر بالا اندازه کفایت نمونه (سلول‌های زرد رنگ) را نشان می‌دهد و بیانگر آن است که متغیرها مورد استفاده به ویژه در مورد کار در روزهای شنبه و یکشنبه / تعطیلات رسمی نیز دارای مقدار کفایت قابل قبول هستند، زیرا مقدار همگی آن‌ها از ۰٫۵ بزرگتر است. در مورد نحوه قضاوت برای شاخص کفایت نمونه به ادامه متن توجه کنید.

حذف این دو متغیر (EF147 ,EF148) باعث افزایش معیار کایزر-مایر-اولکین می‌شود. بیشترین مقدار در همبستگی برای یک همبستگی جزئی (سلول‌های با رنگ سبز) با مقداری برابر  0٫515 نیز بین این دو شاخص یافت می‌شود. به این ترتیب آزمون KMO و بارتلت در تحلیل عاملی اجرا شده و نتایج قابل مشاهده‌اند.

مقدار صفر در این حالت، نشان می‌دهد که مجموع همبستگی های جزئی نسبت به مجموع همبستگی‌ها زیاد است که نشانگر تجزیه و تحلیل عامل نامناسب است. مقدار KMO نزدیک به 1 نشان می‌دهد که مجموع همبستگی‌های جزئی نسبت به مجموع همبستگی‌ها، زیاد نیست و بنابراین نتیجه تجزیه و تحلیل فاکتورها یا تحلیل عاملی باید فاکتورهای متمایز و قابل اتکا ایجاد کند.

توجه داشته باشید که دامنه مقدارهای KMO، بین 0 تا 1 را در بر می‌گیرد. یک قانون کلی برای تفسیر آماری این شاخص به صورت زیر است.

• مقادیر KMO بین 0٫8 و 1 نشان می‌دهد که نمونه برداری برای اجرای تحلیل عاملی اکتشافی (EFA) کافی است.
• مقادیر KMO کمتر از 0٫6 نشان می‌دهد که نمونه‌گیری کافی نیست و باید اقدامات اصلاحی انجام شود. بعضی از نویسندگان حوزه آمار و محققین سقف این مقدار را 0٫5 می‌دانند، بنابراین برای مقادیر بین 0٫5 تا 0٫6 بهتر است خودتان قضاوت را به عهده بگیرید.
• مقادیر KMO نزدیک به صفر به این معنی است که همبستگی‌های جزئی زیادی در مقایسه با مجموع همبستگی‌ها اصلی و حاشیه‌ای وجود دارد. به عبارت دیگر، همبستگی‌های گسترده‌ای وجود دارد که یک مشکل بزرگ برای تحلیل عاملی است.

به عنوان یک مرجع از مقادیر KMO، کایزر اعداد و محدوه‌های زیر را به منظور شرایط کفایت نمونه‌گیری در تحلیل عاملی در نظر گرفته است.

• 0٫00 تا 0٫49 غیر قابل قبول است.
• 0٫50 تا 0٫59 ضعیف.
• 0٫60 تا 0٫69 متوسط.
• 0٫70 تا 0٫79 قابل قبول.
• 0٫80 تا 0٫89 مناسب.
• 0٫۹0 تا 1٫00 عالی.

در کدی که در ادامه متن مشاهده می‌کنید، آزمون KMO و بارتلت در تحلیل عاملی به همراه نتایج بدست آمده برای مجموعه داده mtcars که از مجموعه داده‌های برنامه R است، استفاده شده. در مجموعه داده mtcars اطلاعات و ویژگی‌هایی مختلف 32 خودرو ثبت شده که شامل ۱۱ متغیر است که در ادامه معرفی شده‌اند. باید توجه داشت که بعضی از این متغیرها، کمی و بعضی نیز کیفی هستند.

mpg- مسافت طی شده با یک گالن سوخت، cyl- تعداد سیلندر، disp- فضای کابین (اینچ مکعب)، hp-قدرت موتور (اسب بخار)، drat- نسبت اکسل عقب (چرخ‌دنده‌های دیفرانسیل)، wt- وزن (برحسب ۱۰۰۰ پوند)، qsec- زمان طی کردن یک چهارم مایل برحسب ثانیه، vs- نوع موتور (0=خورچینی، ۱= خطی)، am- نوع گیربکس (۰= اتوماتیک و ۱= دستی) و gear- تعداد دنده‌های جلو، همچنین carb- تعداد کاربراتور.

همانطور که مشاهده می‌کنید، کتابخانه یا بسته parameters برای استفاده از دستور و تابع check_kmo لازم است. به  همین جهت با فرمان library آن را فراخوانی کرده‌ایم. البته اگر این کتابخانه با بسته، از قبل روی نرم افزار R نصب نشده باشد، باید از طریق دستور Install.package ابتدا آن را نصب کنید، سپس در برنامه به کار گیرید. به این ترتیب دسترسی به توابع محاسباتی برای آزمون KMO و بارتلت در تحلیل عاملی در اختیارتان قرار می‌گیرد.

نکته: در مطلب تحلیل عاملی و پیاده‌ سازی آن در پایتون — به زبان ساده، یک مثال کامل براساس کدهای پایتون برای تجزیه و تحلیل عاملی به همراه محاسبات مربوط به آزمون KMO و بارتلت در تحلیل عاملی پیاده سازی شده و قابل دسترس است.

مقدار نهایی برای شاخص KMO برای مجموعه داده mtcars برابر با ۰٫۸۳ است که مناسب بودن اجرای تحلیل عاملی روی این داده‌ها را تضمین می‌کند. به این ترتیب شاید به کمک EFA و محاسبات انجام شده در آزمون KMO و بارتلت در تحلیل عاملی بتوان فاکتورها یا عامل‌هایی از تجمیع بعضی از متغیرها به صورت، «ویژگی‌های موتوری»، «راحتی و آسایش اتاق» و «مصرف بهینه سوخت و کارایی» ایجاد کرد. به یاد دارید که این‌ها، همان متغیرهای پنهان محسوب می‌شوند. در نوشتارهای دیگر به نحوه اجرای این کار و مدل رگرسیونی در نرم‌افزار R اشاره شده است.

خلاصه و جمع‌بندی

همانطور که خواندید، تجزیه کوواریانس و همچنین استفاده از تحلیل‌های عاملی (اکتشافی و تاییدی)، به نمونه و همچنین همبستگی بین متغیرها و ایجاد متغیرهای پنهان مرتبط است. اگر تعداد متغیرهای قابل اندازه‌گیری زیاد باشند، احتیاج داریم به کمک روش‌هایی، حداقل اندازه نمونه برای تحلیل عاملی را مشخص کرده و با توجه به میزان وابستگی بین متغیرها، اطمینان نسبی برای به کارگیری تحلیل عاملی را مشخص و بیان کنیم. شاخص‌ها و آزمون KMO و بارتلت در تحلیل عاملی اکتشافی به این منظور تهیه شده‌اند تا پژوهشگران نسبت به شرایط اجرای تحلیل عاملی (FA) اطمینان کسب کنیم.