آمار توصیفی در SPSS — راهنمای کاربردی

محاسبه شاخصهای آماری به منظور توصیف خصوصیات دادهها از اهمیت زیادی برخوردار است. شاخصهای مرکزی و پراکندگی به همراه شاخصهای تقارن و همبستگی از گونه مقادیر و شاخصهایی هستند که میتوانند ویژگیهای یک مجموعه داده برگرفته از جامعه آماری را بیان کنند. این بخش از محاسبات آماری را شاخصهای توصیفی مینامند. در این نوشتار نحوه محاسبه آمار توصیفی در SPSS را به منظور بدست آوردن این گونه شاخصها مورد بررسی قرار دهیم.
میانگین(Mean)، میانه (Median) و نما (Mode) در گروه شاخصهای مرکزی (Central Tendency) یا تمایل به مرکز قرار میگیرند. از طرفی واریانس (Variance)، انحراف معیار (Standard Deviation) و دامنه تغییرات (Range) شاخصهای پراکندگی (Dispersion) در آمار توصیفی نامیده میشوند. همچنین چولگی (Skewness) و کشیدگی (kurtosis) نیز شاخصهای تقارن عمودی و افقی توزیع فراوانی دادهها را تعیین میکند. از طرفی، ضریبهای همبستگی، شاخصهایی برای نشان داده میزان ارتباط بین دو متغیر بوده و میتوانند وضعیت دو متغیر را نسبت به یکدیگر، نشان دهند. در این نوشتار به فرمولهای محاسباتی برای بدست آوردن این شاخصها اشاره نخواهیم کرد زیرا هر کجا از شاخص آمار توصیفی در SPSS اشاره کردهایم، لینکی هم برای آشنایی بیشتر قرار دادهایم که در آن، نحوه بدست آوردن شاخص نیز قابل مطالعه است.
اگر میخواهید با محیط SPSS و نحوه به کارگیری پنجرههای آن بیشتر آشنا شوید خواندن نوشتار پنجره ویرایشگر داده (Data Editor) در SPSS — راهنمای کاربردی ضروری است. همچنین به منظور آگاهی از خصوصیات نسخه جدید SPSS بهتر است، نوشتار امکانات جدید SPSS نسخه ۲۵ که باید آنها را بدانید را نیز بخوانید. همچنین مطالعه مطالب آشنایی با مقدمات آمار و کاربردهای آن — از صفر تا صد و شاخص های آمار توصیفی در علم داده — راهنمای کاربردی نیز خالی از لطف نیست.
آمار توصیفی در SPSS
شناخت جامعه آماری (Population) اصلیترین بخش در تحلیل دادههای آماری است. همه تلاش دانشمندان داده (Data Scientists) آن است که خصوصیات و ویژگیهای جامعه آماری را بشناسند و روابط بین متغیرها را تشخیص دهند.
یکی از روشهای ساده ولی موثر در این مهم، محاسبه و به کارگیری شاخصهای آمار توصیفی است. شاخصهای توصیفی معمولا به پنج گروه تقسیم میشوند.
- شاخصهای تمایل به مرکز: این گروه از شاخصهای آماری، امکان خلاصهسازی و یا جمعبندی مقادیر را در یک عدد یا نقطه فراهم میآورند. برای مثال میانگین (Mean) و میانه (Median) و همینطور نما (Mode) در این گروه از شاخصها قرار دارند.
- شاخصهای چندکی: چندکها (Quantile)، نقاطی را مشخص میکنند که درصد خاصی از مشاهدات از آنها کمتر هستند. برای مثال اگر بگوییم که مقدار ۴۰، صدک دهم دادهها است به این معنی است که ۱۰ درصد دادهها مقداری کوچکتر یا مساوی با ۴۰ دارند. معمولا چندکها مرتبط با توزیع یا فراوانی دادهها هستند. ممکن است چندکها را به صورت صدک (Percentile)، دهک (decile)، یا چارک (Quartile) نشان دهند. صدکها، مجموعه دادهها را به صد قسمت مساوی تقسیم میکنند. مشخص است که به این ترتیب نود و نه صدک وجود خواهد داشت. همچنین تعداد دهکها نیز ۹ تا است که جامعه را به ۱۰ قسمت مساوی تقسیم میکنند. چارکها نیز که دادهها را به چهار بخش مساوی تقسیم میکنند، چارک اول، دوم و سوم نامیده میشوند.
- شاخصهای پراکندگی: در گروه شاخصهای پراکندگی، میزان دوری دادههای از یکدیگر سنجیده میشود. برای مثال مجموع فاصله همه دادهها از یکدیگر را میتوان مبنایی برای مفهوم پراکندگی در نظر گرفت. البته تعداد محاسبات با افزایش تعداد نقاط بسیار زیاد خواهد شد. اغلب برای محاسبه پراکندگی از محاسبات سادهتری مانند دامنه تغییرات (Range) که میزان حداکثر پراکندگی را محاسبه میکند، استفاده میشود. همچنین شاخصهای انحراف معیار (Standard Deviation) و واریانس (Variance) که متوسط فاصله نقاط از یک نقطه مرکزی را ملاک پراکندگی قرار میدهد، از شاخصهای محبوب برای تعیین پراکندگی محسوب میشوند.
- شاخصهای تقارن: از آنجایی که منحنی توزیع و نرمال به عنوان یک حالت ایدهآل برای پدیدههای تصادفی در نظر گرفته شده است، اغلب دوست داریم، دادههایی که با آن سروکار داریم نیز دارای توزیع نرمال بوده و منحنی فراوانی (هیستوگرام) آن شبیه نمودار توزیع نرمال باشد. این منحنی متقارن بوده و زنگی شکل است. هر گونه عدم تقارن در دادهها نسبت به توزیع و منحنی نرمال بوسیله شاخصهای تقارن، سنجیده میشوند. چولگی (Skewness) و کشیدگی (Kurtosis) از این گونه شاخصها هستند که اولی تقارن افقی و دوم تقارن عمودی را نسبت به توزیع نرمال میسنجد. در صورتی که توزیع و منحنی فراوانی دادهها، شبیه توزیع نرمال باشد، مقادیر این شاخصهای به صفر نزدیک خواهد بود.
- شاخصهای ارتباط بین دو یا چند متغیر: اگر جامعه آماری مورد بررسی دارای دو یا چند ویژگی باشد، لازم است که ارتباط بین این متغیرها یا ویژگیها نیز به عنوان شاخصی برای توصیف ارتباط بین متغیرها محاسبه شود. ضریب همبستگی و شیوههای مختلف محاسبه آن، شاخصهایی در این زمینه ارائه میدهند. برای مثال میتوان به ضریب همبستگی پیرسون و ضریب همبستگی اسپیرمن اشاره کرد. البته ضریب همبستگی جزئی نیز نحوه محاسبه ارتباط بین دو متغیر با حذف اثر متغیر مداخلهگر را تعیین میکند که در این متن به آن نمیپردازیم. در نوشتار دیگری با عنوان ضریب همبستگی جزئی (Partial Correlation) — به زبان ساده به این موضوع پرداختهایم.
در ادامه سعی میکنیم این شاخصها را به کمک نرمافزار SPSS و دستورات سادهای که فرا خواهیم گرفت، محاسبه کنیم. برای نمایش نحوه محاسبات و خروجیها، از یک فایل داده SPSS استفاده کردهایم که میتوانید آن را از اینجا با قالب فشرده (ZIP)، دریافت کنید. این فایل شامل چهار متغیر و ۱۲ مشاهده است که در آن میزان فروش و تعداد سفارش دو نوع کالا را برحسب سه شیفت کاری مختلف، ثبت شده.
آمار توصیفی در SPSS با دستور Frequency
یکی از شیوههای ساده برای محاسبه شاخصهای مرکزی و پراکندگی و همچنین تقارن، استفاده از دستور Frequency است. مسیر دسترسی به آن به شکل زیر است:
Analysis ---> Descriptive Statistics ---> Frequency
در تصویر زیر پنجره پارامترهای این دستور را مشاهده میکنید. به منظور محاسبه شاخصهای آمار توصیفی برای هر یک از متغیرها، کافی است که نام متغیر را در کادر Variable قرار دهیم.
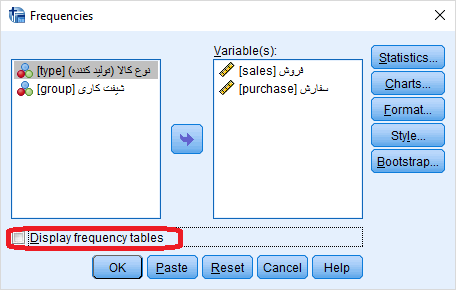
نکته: از آنجایی که فقط به شاخصهای آمار توصیفی علاقمندیم و نمیخواهیم جدول فراوانی را در خروجی ظاهر کنیم، گزینه Display frequency tables را غیرفعال کردهایم.
برای تعیین شاخص مورد نظر هنگام اجرای دستور Frequency، از دکمه Statistics استفاده کرده و از داخل پنجره آن، شاخصهای آمار توصیفی را انتخاب میکنیم.
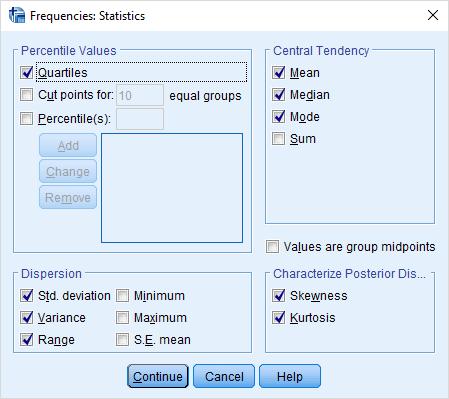
همانطور که در تصویر بالا دیده میشود، شاخصهای تمرکز، چندکها، شاخصهای پراکندگی و تقارن علامت خوردهاند. با کلیک بر روی دکمه Continue به پنجره اصلی بازگشته و با فشردن دکمه OK، محاسبات صورت گرفته و خروجی به صورت زیر ظاهر خواهد شد.
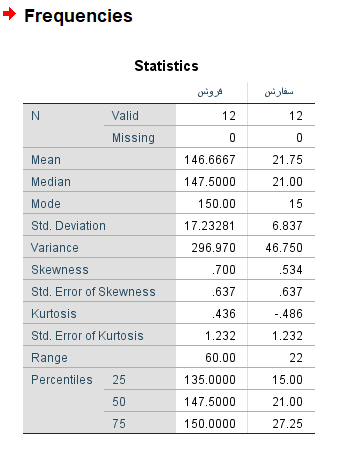
از آنجایی که دو متغیر را انتخاب کردهایم، شاخصهای آمار توصیفی این دو متغیر در کنار هم ظاهر شده و امکان مقایسه را فراهم میآورد. برای مثال تعداد سفارشات دارای میانگینی برابر با حدود 21٫75 واحد است در حالیکه متوسط فروش 146٫66 محاسبه شده است.
آمار توصیفی در SPSS با دستور Descriptive
در این قسمت محاسباتی که در بالا به آن اشاره کردیم، توسط دستور Descriptive در SPSS انجام میدهیم. البته مشخص است که نتایج بدست آمده با قسمت قبل یکسان خواهد بود و فقط در شکل و شیوه نمایش خروجی تفاوت وجود خواهد داشت.
مسیر دسترسی به این دستور به صورت زیر است:
Analysis ---> Descriptive Statistics ---> Descriptive
پارامترهای این دستور در تصویر زیر قابل مشاهده است. شاخصهایی که به طور پیشفرض در این دستور محاسبه میشوند شامل میانگین (Mean)، انحراف استاندارد (Standard Deviation)، حداقل (Minimum) و حداکثر (Maximum) و البته تعداد مشاهدات (N)، است.
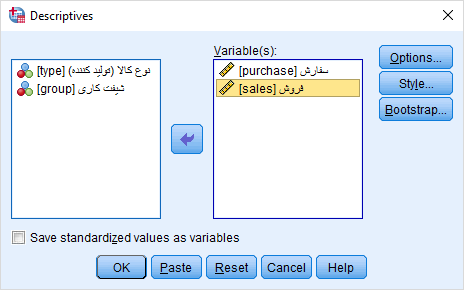
اگر به شاخصهای دیگری احتیاج دارید با انتخاب دکمه Options، امکان انتخاب آنها را خواهید داشت. با این کار پنجرهای مطابق با تصویر زیر ظاهر خواهد شد.
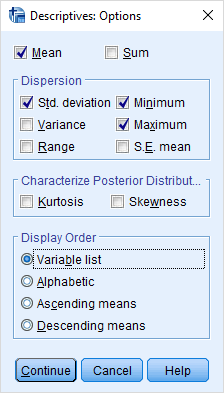
همانطور که مشاهده میکنید، در اینجا امکان محاسبه چندکها وجود ندارد. با کلیک روی دکمه Continue و بازگشت به پنجره اصلی، دکمه OK را فشار دهید تا خروجی به صورت زیر ظاهر شود.
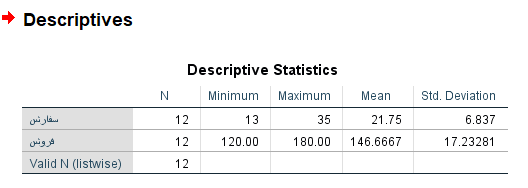
آمار توصیفی در SPSS با دستور Explore
یکی از دستورات بسیار موثر و کامل در محاسبات آمار توصیفی، دستور Explore است که مجموعهای از نمودارها و جدولها را به عنوان خروجی ظاهر میکند. البته از آنجایی که در این نوشتار فقط به بحث آمار توصیفی توجه داریم، گزینههای مرتبط با این موضوع را مورد اشاره قرار خواهیم داد. نحوه دسترسی به این دستور به صورت زیر است.
Analysis ---> Descriptive Statistics ---> Explore
پارامترهای این دستور در تصویر زیر قابل مشاهده است. متغیرهایی که قرار است شاخصهای آمار توصیفی برایشان محاسبه شود باید در کادر Dependent List قرار گیرند. البته این امکان نیز در این دستور وجود دارد که شاخصهای آمار توصیفی را برای دستههایی از مشاهدات که توسط یک یا چند متغیر طبقهای تعیین میشوند به طور جداگانه محاسبه و نمایش داد. در اینجا به طور مثال از متغیرهای type و group به این منظور استفاده کردهایم.
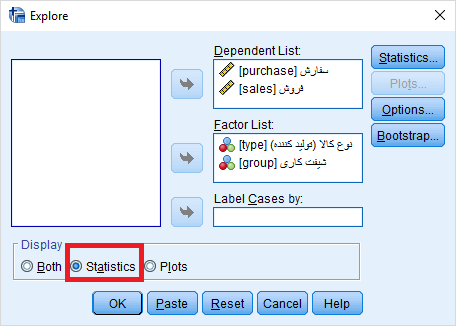
همچنین از آنجایی که در خروجی فقط به آمار توصیفی احتیاج داریم، گزینه Statistics را در قسمت Display انتخاب کردهایم. خروجی به صورت زیر خواهد بود. مشخص است که برای هر سطوح از متغیر طبقهای شاخصهای آمار توصیفی بدست آمده است. از آنجایی که دو متغیر طبقهای معرفی شده، چند جدول به عنوان خروجی اصلی ظاهر شده است. ابتدا جدول مربوط به میزان سفارش ظاهر شده که در آن نتایج مربوطه، براساس نوع کالا (تولید کننده) طبقهبندی شده است.
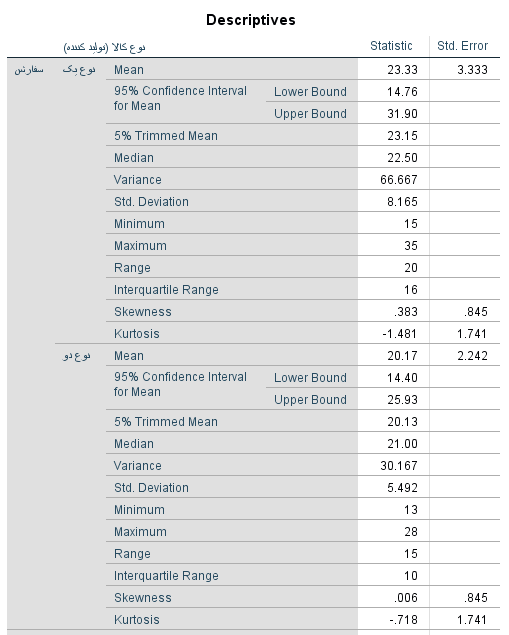
سپس محاسبات برمبنای میزان فروش صورت گرفته است. از آنجایی که تعداد سطرهای این جدول زیاد است، از نمایش بقیه سطرها، صرف نظر کردهایم. همانطور که گفته شد، ارتفاع این جدول زیاد بوده و امکان نمایش اطلاعات در یک مکان و مقایسه را سخت میکند. بهتر است آن را ویرایش کرده و نحوه نمایش اطلاعات را تغییر دهیم. برای این کار روی جدول خروجی Descriptive، دوبار کلیک میکنیم و جای شیفتکاری (group) را در جدول محوری (Pivot Table) تغییر میدهیم.

به این ترتیب جدولهای مربوط شاخصهای آمار توصیفی مقدار سفارش و میزان فروش به تفکیک سطوح متغیر طبقهای شیفتکاری به شکل منظمتری مشخص خواهد شد.
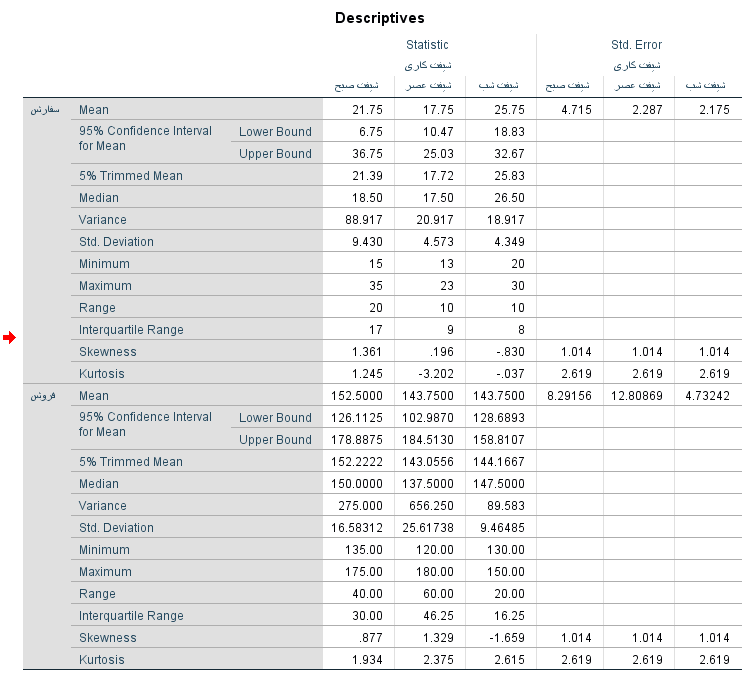
همانطور که مشاهده میکنید، زمانی که سطوح یک متغیر طبقهای زیاد باشد، نمایش اطلاعات به این فرم مناسبتر خواهد بود و امکان مقایسه بین شاخصها در گروه یا دستهها مختلف به راحتی میسر میشود.
آمار توصیفی دو متغیره در SPSS
گاهی لازم است که ارتباط بین دو متغیر سنجیده شود. به این ترتیب میتوانیم میزان وابستگی بین آن دو را اندازهگیری کنیم. با این کار قدرت پیشگویی یکی برحسب دیگری بوجود میآید. برای مثال اگر بتوانیم تشخیص دهیم که چه ارتباطی بین میزان فروش و مقدار سفارش وجود دارد، برنامهریزی خرید بهتری خواهیم داشت و از طرفی مقدار سفارش را برحسب میزان فروش تعیین میکنیم.
برای محاسبه میزان وابستگی بین دو متغیر از نوع کمی (Scale) از شاخصهای توصیفی به نام «ضریب همبستگی پیرسون» (Pearson Correlation Coefficient) و «ضریب همبستگی رتبهای اسپیرمن» (Spearman's Rank Correlation Coefficient) استفاده خواهیم کرد که خوشبختانه هر دو در نرمافزار SPSS قابل محاسبه هستند.
برای دسترسی به پنجره و تنظیم پارامترهای لازم برای این گونه محاسبات، مسیر زیر را طی کنید.
Analysis ---> Correlation ---> Bivariate
پارامترهای این دستور در تصویر زیر قابل مشاهده است. ابتدا باید دو متغیری که قرار است ضریب همبستگی برایشان محاسبه شود را در کادر Variables قرار دهید. البته ممکن است بیش از دو متغیر نیز در این قسمت ظاهر شوند، با این کار ضریب همبستگی برای ترکیبهای دو تایی از آنها محاسبه و نمایش داده میشود. در اینجا از متغیرهای Sale و Purchase استفاده کردهایم.
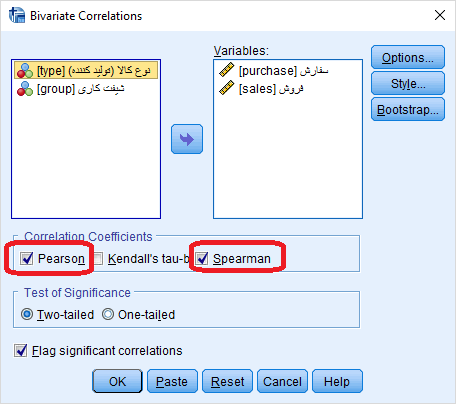
با فشردن دکمه OK، محاسبات صورت گرفته و خروجی ظاهر خواهد شد.
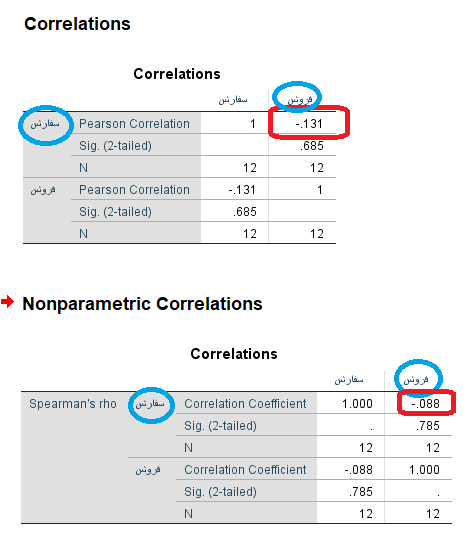
همانطور که دیده میشود، مقدار ضریب همبستگی پیرسون بین میزان فروش و مقدار سفارش منفی است که نشانگر ارتباط معکوس بین این دو متغیر است. مقدار این شاخص برابر با است که همبستگی ضعیف بین این دو متغیر را نشان میدهد. از طرفی ضریب همبستگی رتبهای اسپیرمن نیز با مقدار بیانگر ارتباط بسیار کم بین این دو متغیر است. در هر دو جدول آزمون مربوط به معنیداری ضریب همبستگی نیز صورت گرفته که با توجه به بزرگ بودن Sig در هر کدام از آنها، فرض صفر که مرتبط با بیمعنی بودن همبستگی دو متغیر است، تایید میشود. در نتیجه میتوان گفت که این نمونه دلیلی مبنی بر ارتباط بین میزان فروش و مقدار سفارش ارائه نکرده است.
خلاصه و جمعبندی
در این نوشتار با شاخصهای آمار توصیفی در SPSS و نحوه محاسبه آنها با شیوه و دستورات مختلف آشنا شدیم. هر چند نتایج شاخصهای آماری با روشهای مختلف یکسان است ولی معمولا نوع خروجی و نحوه بهرهبرداری از آنها متفاوت است. به همین دلیل فراگیری شیوههای مختلف انجام این گونه محاسبات در این نرمافزار میتواند گزارشهای متنوع و مناسبی برایتان تولید کند. البته برای تهیه گزارش نهایی میتوانید خروجیهای SPSS را به دیگر برنامهها مانند نرمافزار MS-Word وارد کنید تا با گزارش مکتوبی که تهیه کردهاید، صفحهبندی شده و هماهنگ باشد.
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای SPSS
- آموزش آماده سازی داده ها برای تحلیل آماری در SPSS
- مجموعه آموزشهای آمار و احتمال
- نمایش و رسم نمودار برای دادهها — معرفی و کاربردها
- رسم نمودار در پایتون با Matplotlib — راهنمای کاربردی
- نمودار جعبه ای (Boxplot) و رسم آن در پایتون – به زبان ساده
^^














بسیار عالی
درود
آقای “ری بد” آمار رو بسیار عالی تدریس می کنند و بنده از آموزشهایی که تهیه کردم راضی هستم و اون رو به دوستان علاقمند و نیازمند پیشنهاد می کنم.
با سپاس