روشهای رگرسیون در R — کاربرد در یادگیری ماشین (قسمت اول)

در نوشتار فرادرس با عنوان آموزش رگرسیون — مجموعه مقالات جامع وبلاگ فرادرس انواع روشهای رگرسیونی یک و چند گانه، بخصوص روشهایی که در «یادگیری ماشین» (Machine Learning) به کار میروند، معرفی شدند. همچنین در مطلب رگرسیون خطی — مفهوم و محاسبات به زبان ساده شیوه محاسبات رگرسیون خطی ساده و آزمونهای مربوط به آن به طور کامل شرح داده شد.
ولی در این مطلب به شیوه پیادهسازی محاسبات رگرسیون در زبان برنامهنویسی R میپردازیم. در این بین از محیط Rstudio برای ورود و اجرای کدها بهره برده و خروجیها را دریافت میکنیم. در قسمت اول به بررسی رگرسیون خطی ساده و چند گانه پرداخته و در قسمت دوم نیز روشهای رگرسیون برای دادههای طبقهای و رگرسیون گام به گام را معرفی خواهیم کرد و کدهای مربوط به پیادهسازی این تکنیکها در زبان برنامهنویسی R معرفی خواهند شد.
روشهای رگرسیونی
یکی از روشهای معمول در یادگیری ماشین، تکنیک رگرسیون یا برازش خط است که به طور گسترده در «علم داده» (Data Science) به کار گرفته میشود.
برای مثال به منظور شناسایی پیام یا «هرزنامهها» (Spams) از روشهای یادگیری ماشین کمک گرفته میشود که وابسته به محاسبات رگرسیونی هستند.
بعضی از کاربردهای یادگیری ماشین در ادامه فهرست شدهاند.
- شناسایی پیامهای ناخواسته یا هرزنامهها در صندوق پست الکترونیک
- بخشبندی مشتریان به منظور ارسال تبلیغات موثرتر
- کاهش معاملات جعلی کارت اعتباری
- بهینهسازی مصرف انرژی در خانه و ساختمانهای اداری
- تشخیص چهره
قبل از شروع پیادهسازی الگوریتمهای یادگیری ماشین و رگرسیون، بهتر است ابتدا تفاوت «یادگیری نظارت شده» (Supervised Learning) و «یادگیری نظارت نشده» (Unsupervised Learning) را یادآوری کنیم.
یادگیری نظارت شده
اگر «دادههای آموزشی» (Training Data) شامل برچسب یا متغیری باشند که نشاندهنده تعلق هر مشاهده یه یک گروه باشد، از الگوریتمهای یادگیری نظارت شده استفاده خواهیم کرد. با این کار با استفاده از الگویی که مدل یادگیری نظارت شده ایجاد میکند، میتوانیم برچسب تعلق به گروه را برای مشاهدات جدیدی که دارای برچسب نیستند، تعیین کنیم.
برای اجرای یادگیری نظارت شده معمولا از دو روش استفاده میشود.
«طبقهبندی» (Classification) یا «ردهبندی» (Discriminant Analysis) یکی از پرکاربردترین تکنیکهای آماری به منظور شناسایی برچسب برای مشاهدات جدید است. یکی از کاربردهای این روشها، تشخیص هرزنامهها (Spam Filtering) است. به این ترتیب الگوریتم براساس مثالهایی که از قبل آموخته، قاعدهای برای تشخیص سالم یا ناسالم بودن نامه الکترونیکی پیدا میکند.
«روشهای رگرسیون» (Regression Methods) نیز از تکنیکهای معمول برای پیشبینی مقدار «متغیر پاسخ» (Response) براساس مقدار «متغیرهای توصیفی» (Explanatory) است. گاهی متغیر پاسخ را «متغیر وابسته» (Dependent Variable) و متغیرهای توصیفی را «متغیرهای مستقل» (Independent Variable) نیز مینامند.
برای مثال به کمک روشهای رگرسیونی میتوان ارزش بازار سهام را پیشبینی کرد. در ادامه الگوریتمهای پایهای که در یادگیری نظارت شده به کار میرود، معرفی شدهاند.
- رگرسیون خطی (Linear Regression)
- رگرسیون لجستیک (Logistic Regression)
- نزدیکترین همسایه (K-Nearest Neighbor- KNN)
- ماشین بردار پشتیبان (Support Vector Machine-SVM)
- درخت تصمیم و جنگل تصادفی (Decision Tree and Random Forest)
- شبکه عصبی (Neural Network)
یادگیری نظارت نشده
در یادگیری نظارت نشده، دادههای آموزشی بدون برچسب هستند در نتیجه مدل یادگیری نظارت نشده، سعی میکند بدون هیچ مرجع یا الگوی اولیهای، دستهبندی و گروهبندی را انجام دهد. در لیست زیر بعضی از الگوریتمهای که در یادگیری نظارت نشده به کار میروند، معرفی شدهاند.
- خوشهبندی k-میانگین (K-mean Cluster Analysis)
- خوشهبندی سلسله مراتبی (Hierarchical Cluster Analysis)
- روش EM و خوشهبندی برمبنای مدل توزیع (Expectation Maximization - EM Model Based Clustering)
- تحلیل مولفههای اصلی (Principal Component Analysis- PCA)
رگرسیون خطی ساده
رگرسیون خطی به یک سوال ساده پاسخ میدهد: چگونه میتوان مقدار ارتباط بین یک متغیر هدف (Target) و مجموعهای از متغیرهای پیشگو (Predictors) را اندازه گرفت؟
در این حال متغیر هدف همان متغیر وابسته و متغیرهای پیشگو نیز همان متغیرهای مستقل هستند. مدل خطی در رگرسیون ساده به صورت زیر نوشته میشود:
در این رابطه متغیر وابسته، متغیر مستقل و نیز مولفه خطای مدل محسوب میشود. همچنین پارامترهای این مدل خطی ، «عرض از مبدا» (Intercept) و شیب خط (Slope) است.
- متغیر وابسته، y = Dependent Variable
- متغیر مستقل، x = Independent Variable
- جمله خطا Random Error Component
- عرض از مبدا Intercept
- شیب خط (ضریب متغیر مستقل) Coefficient of x
به تصویر زیر توجه کنید.
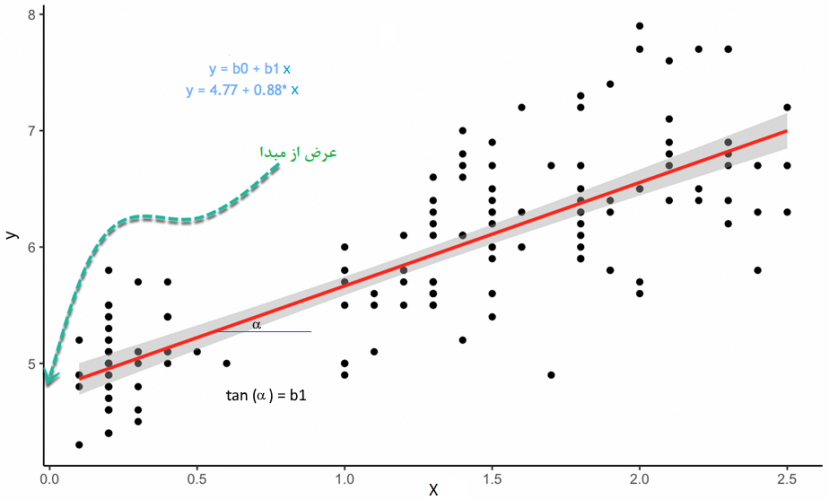
شیب خط در حالت رگرسیون خطی ساده، نشان میدهد که میزان حساسیت متغیر وابسته به متغیر مستقل چقدر است. به این معنی که متوجه میشویم با افزایش یک واحد به مقدار متغیر مستقل چه میزان متغیر وابسته تغییر خواهد کرد. عرض از مبدا نیز بیانگر مقداری از متغیر وابسته است که به ازاء صفر بودن مقدار متغیر مستقل محاسبه میشود. به شکل دیگر میتوان مقدار ثابت یا عرض از مبدا را مقدار متوسط متغیر وابسته به ازاء حذف متغیر مستقل در نظر گرفت.
به منظور برآورد پارامترهای مدل رگرسیون ساده از روش «کمترین مربعات عادی» (Ordinary Least Square- OLS) استفاده میکنیم. این روش با کمینهسازی جمع مربعات جملههای خطا، عمل برآورد پارامترها را انجام میدهد. در اینجا جملههای خطا همان تفاوت بین مقدار واقعی و پیشبینی شده برای متغیر پاسخ یا متغیر وابسته است.
ولی بهتر است قبل از برآورد پارامترها و تعیین مدل رگرسیونی، به رابطه بین دو متغیر توجه کنیم. رابطه بین دو متغیر مستقل و پاسخ را میتوان بوسیله نمودار پراکندگی (Scatterplot) نمایش داد.
نمودار پراکندگی (Scatterplot)
در اینجا از مجموعه داده سادهای که در مورد میزان قد و وزن فرد است استفاده میکنیم. این اندازهها برای ۱۵ مشاهده ثبت شده و از اینجا قابل دریافت است. این فایل به صورت فشرده بوده ولی با باز کردن آن امکان دسترسی به فایلی با قالب CSV وجود دارد. این گونه فایلها، اطلاعات را به صورت متنی ذخیره کرده ولی ساختاری جدولی دارند. نمایش دادن اطلاعات این فایلها بوسیله نرمافزار اکسل امکانپذیر است. برای رسم نمودار پراکندگی از کتابخانه ggplot2 استفاده کرده و کدهای زیر را اجرا میکنیم.
1library(ggplot2)
2path <- 'women.csv'
3df <-read.csv(path)
4ggplot(df,aes(x=height, y = weight))+
5 geom_point()در این مجموعه داده، در متغیر weight وزن و در متغیر height قد فرد ثبت شده است. با اجرای این دستورات در محیط Rstudio، خروجی به صورت زیر ظاهر خواهد شد. همانطور که انتظار داشتیم، ۱۵ نقطه در مختصات صفحه ترسیم شده که هر نقطه بیانگر قد و وزن یک فرد است. از آنجایی اطلاعات ۱۵ نفر در دسترس بود، ۱۵ نقطه نیز در نمودار ظاهر شده.
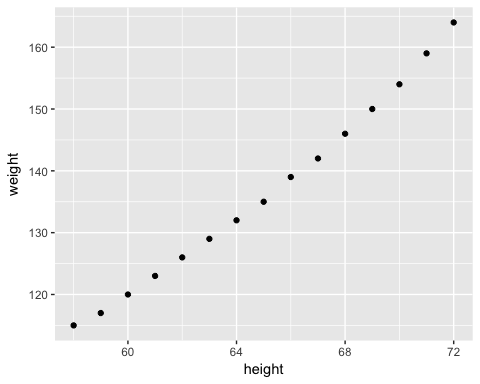
براساس این نمودار، وجود رابطه خطی بین دو متغیر مشاهده میشود و مشخص است که با افزایش قد، وزن افراد نیز بیشتر میشود. حالا به کمک برآورد پارامترهای مدل رگرسیونی، ارتباط بین قد و وزن به صورت یک رابطه ریاضی نوشته خواهد شد.
برآوردهای کمترین مربعات
در برآورد پارامترهای رگرسیون به کمک تکنیک OLS، از مشتق و کمینهسازی مجموع مربعات خطا استفاده میشود که محاسبات مربوط به آن در نوشتار رگرسیون خطی — مفهوم و محاسبات به زبان ساده به تفصیل بیان شده است. بر این اساس، برآورد پارامترهای مدل خطی به صورت زیر خواهند بود.
که در آن و میانگین و هستند. همانطور که قبلا هم گفته شد اگر متغیر مستقل حذف شود، پارامتر همان میانگین متغیر وابسته یا پاسخ خواهد بود.
برای راحتی محاسبات، میتوان برآورد را به فرم دیگری نیز نوشت:
در زبان برنامهنویسی R برای محاسبه واریانس از دستور var و به منظور محاسبه کوواریانس از تابع cov استفاده میشود.
1beta1 <- cov(df$height, df$weight) / var (df$height)
2beta1با اجرای این دستورات مقدار 3.4 برای ضریب متغیر حاصل میشود. همچنین برای بدست آوردن عرض از مبدا، محاسبات را به صورت زیر انجام میدهیم.
1beta0 <- mean(df$weight) - beta1 * mean(df$height)
2beta0خروجی این دستورات نیز مقدار 87.51667- است. به این ترتیب مدل رگرسیونی برای رابطه بین قد و وزن به صورت زیر نوشته خواهد شد:
همانطور که دیده میشود، محاسبات مربوط به ایجاد مدل رگرسیون خطی ساده، پیچیده نیست و به راحتی به کمک توابع معمول در R قابل محاسبه است. ولی در زبان برنامهنویسی R توابعی وجود دارند که برای مدل رگرسیونی چند گانه به کار رفته و محاسبات پیچیده ماتریسی را به منظور برآورد پارامترهای این مدل انجام میدهند.
رگرسیون چند گانه
کاربرد اصلی رگرسیون در حالت پیچیدهتر آن یعنی «رگرسیون چند گانه» (Multiple Regression) است. مدل رگرسیون چند گانه دارای چندین متغیر مستقل و به همان تعداد نیز دارای پارامتر است (البته در حالتی که عرض از مبدا وجود داشته باشد، تعداد پارامتر یکی بیشتر از تعداد متغیرها است).
در این حالت به جای برازش یک خط در مدل، از صفحههای دو تا چند بعدی استفاده میشود.
حالت عمومی برای مدل رگرسیون چندگانه با k متغیر در زیر نوشته شده است:
اگر ماتریس متغیرها، ماتریس ضرایب و نیز بردار مقدارهای متغیر پاسخ باشد، میتوان رابطه بالا را به صورت ماتریسی نوشت. به این ترتیب معادله ماتریسی رگرسیون به صورت زیر درخواهد آمد:
واضح است که در رابطه بالا، بردار جملات خطا با نمایش داده شده است.
در هنگام برآورد پارامترهای مدل رگرسیونی باید فرضیاتی که برمبنای آن مدل شکل گرفته را در نظر داشت. این فرضیات برای کمترین مجموع مربعات عادی (OLS) و جمله خطا، در زیر آمده است:
- میانگین جمله خطا صفر است.
- واریانس هر مولفه از جمله خطا ثابت و برابر با است.
- جملات خطا از یکدیگر مستقل هستند.
- جملات خطا دارای توزیع نرمال هستند. در حالت چند گانه نیز جملات خطا دارای توزیع چند متغیره نرمال خواهند بود.
به این ترتیب اگر ماتریس واریانس-کوواریانس بردار خطا را با نشان دهیم خواهیم داشت:
براساس محاسبات ماتریسی و کمینهسازی بردار خطا، برآوردگرهای مربوط به مدل به صورت زیر محاسبه میشود.
توجه داشته باشید که منظور از ترانهاده و نیز معکوس ماتریس است.
در این مرحله از مجموعه داده mtcars که اطلاعات و ویژگیهایی مختلف 32 خودرو در آن ثبت شده کمک میگیریم و مدل رگرسیونی چند گانه را برای پیشبینی مسافت طی شده با یک گالن سوخت ایجاد میکنیم. این مجموعه داده به طور خودکار در R بارگذاری شده است. متغیرهای مربوط mtcars در جدول زیر معرفی شدهاند.
| ردیف | نام متغیر | شرح |
| ۱ | mpg | مسافت طی شده با یک گالن سوخت |
| ۲ | cyl | تعداد سیلندر |
| ۳ | disp | فضای کابین (اینچ مکعب) |
| ۴ | hp | قدرت موتور (اسب بخار) |
| ۵ | drat | نسبت اکسل عقب (چرخدندههای دیفرانسیل) |
| 6 | wt | وزن (برحسب ۱۰۰۰ پوند) |
| ۷ | qsec | زمان طی کردن یکچهارم مایل برحسب ثانیه |
| ۸ | vs | نوع موتور (0=خورچینی، ۱= خطی) |
| 9 | am | نوع گیربکس (۰= اتوماتیک و ۱= دستی) |
| ۱۰ | gear | تعداد دندههای جلو |
| 11 | carb | تعداد کاربراتور |
در این مثال، برای ایجاد مدل رگرسیونی، تنها از «متغیرهای کمی» (Quantity) استفاده میکنیم و «متغیرهای کیفی» (Quality) را نادیده میگیریم. کدهای زیر به منظور کنار گذاشتن متغیرهای کیفی نوشته شدهاند. البته همانطور که دیده میشود متغیرهای cyl , gear و carb متغیرهای عددی هستند ولی در واقع یک متغیر کمی محسوب نمیشوند.
1library(dplyr)
2df <- mtcars % > %
3select(-c(am, vs, cyl, gear, carb))
4glimpse(df)با اجرای این کدها، خروجی به صورت زیر خواهد بود.
1## Observations: 32
2## Variables: 6
3## $ mpg <dbl> 21.0, 21.0, 22.8, 21.4, 18.7, 18.1, 14.3, 24.4, 22.8, 19....
4## $ disp <dbl> 160.0, 160.0, 108.0, 258.0, 360.0, 225.0, 360.0, 146.7, 1...
5## $ hp <dbl> 110, 110, 93, 110, 175, 105, 245, 62, 95, 123, 123, 180, ...
6## $ drat <dbl> 3.90, 3.90, 3.85, 3.08, 3.15, 2.76, 3.21, 3.69, 3.92, 3.9...
7## $ wt <dbl> 2.620, 2.875, 2.320, 3.215, 3.440, 3.460, 3.570, 3.190, 3...
8## $ qsec <dbl> 16.46, 17.02, 18.61, 19.44, 17.02, 20.22, 15.84, 20.00, 2...با استفاده از تابع که مخفف عبارت Linear Model است محاسبات مربوط به مدل رگرسیونی انجام میشود. پارامترهای این تابع در زیر معرفی شدهاند.
1lm(formula, data, subset)
2Arguments:
3 -formula: The equation you want to estimate
4 -data: The dataset used
5 -subset: Estimate the model on a subset of the datasetهمانطور که مشخص است پارامتر اول formula است که باید در آن متغیرهای مستقل و وابسته را معرفی کرد. همچنین پارامتر data نیز مجموعه داده را مشخص میکند. اگر لازم است برای بخشی از دادهها، مدل برازش شود، با پارامتر subset این کار صورت میگیرد. کد مربوط به برآورد پارامترهای رگرسیونی برای مثال خودروها در ادامه دیده میشود.
1model <- mpg~disp + hp + drat + wt
2fit <- lm(model, df)
3fitبا توجه به عبارت سطر اول، ارتباط بین متغیر وابسته و متغیرهای مستقل به صورت زیر خواهد بود. مشخص است که این رابطه خطی بین متغیرها و البته بین پارامترها یا ضریب است.
نکته: توجه داشته باشید که منظور از مدل رگرسیون خطی، وجود رابطه خطی بین پارامترها است و ممکن است که رابطه بین متغیرها خطی نباشد. برای مثال اگر یک متغیر به صورت مربع در مدل ظاهر شود، باز هم مدل خطی است زیرا میتوان مثلا میتوان را با نام متغیر جدید به صورت نوشت و برحسب متغیرها، مدل را خطی نمایش داد.
مشخص است که علامت ~ جایگزین علامت = شده و x نیز به جای اسامی متغیرها نوشته شده است. اگر میخواهید مدل بدون عرض از مبدا نوشته شود کافی است در انتهای تابع مقدار ۱- را به عنوان یک پارامتر قرار دهید.
خروجی دستور بالا به شکل زیر نمایش داده میشود.
1Call:
2lm(formula = model, data = df)
3
4Coefficients:
5(Intercept) disp hp drat wt
6 29.148738 0.003815 -0.034784 1.768049 -3.479668به این ترتیب برآورد پارامترها انجام شده و توسط آنها میتوان مقدار مسافت طی شده یا یک گالن سوخت را برای مشاهده جدید پیشبینی کرد. مشخص است که برای مثال ضریب متغیر wt برابر با 3.479668- و عرض از مبدا نیز 29.148738 است.
اگر لازم است که مشخصات بیشتری را در مورد مدل برازش شده دریافت کنید کافی است دستور summary را اجرا نمایید. با اجرای فرمان خروجی به صورت زیر ظاهر میشود.
1all:
2lm(formula = model, data = df)
3
4Residuals:
5 Min 1Q Median 3Q Max
6-3.5077 -1.9052 -0.5057 0.9821 5.6883
7
8Coefficients:
9 Estimate Std. Error t value Pr(>|t|)
10(Intercept) 29.148738 6.293588 4.631 8.2e-05 ***
11disp 0.003815 0.010805 0.353 0.72675
12hp -0.034784 0.011597 -2.999 0.00576 **
13drat 1.768049 1.319779 1.340 0.19153
14wt -3.479668 1.078371 -3.227 0.00327 **
15---
16Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
17
18Residual standard error: 2.602 on 27 degrees of freedom
19Multiple R-squared: 0.8376, Adjusted R-squared: 0.8136
20F-statistic: 34.82 on 4 and 27 DF, p-value: 2.704e-10نتایجی که از خروجی بالا خواهیم گرفت، در فهرست زیر خلاصه شده است:
- با توجه به ضرایب متغیرها در جدول بالا، مشخص است که رابطه قوی ولی منفی بین وزن خودرو (wt) و مسافتی که با یک گالن بنزین پیموده میشود (mpg) وجود دارد. به این معنی که هرچه خودرو سنگینتر باشد، مسافت کمتری را با یک گالن سوخت طی میکند.
- رابطه منفی بین میزان مسافت طی شده با هر گالن سوخت (mpg) و قدرت موتور (hp) وجود دارد. به این معنی که برای موتورهای پرقدرت، مسافت طی شده کمتر خواهد بود.
- از لحاظ آماری، فقط متغیر وزن (wt) و قدرت موتور (hp) بر روی مسافت طی شده (mpg) دارای تاثیر است. زیرا مقدار p-value که در جدول با علامت نشان داده شده است، برای آنها کمتر از ۰.05 است. البته عرض از مبدا نیز به همین علت مخالف صفر در نظر گرفته خواهد شد. بقیه متغیرها هرچند ممکن است دارای ضریب مثبت باشند ولی به علت عدم پذیرش آنها در مدل توسط معیار p-value که در ستون دیده میشود، نادیده گرفته خواهند شد.
- مقدار اصلاح شده () واریانس یا پراکندگی دادهها را که توسط مدل شناسایی شده، محاسبه کرده است. بزرگ بودن این مقدار دلیل بر مناسب بودن مدل است. در اینجا مقدار اصلاح شده حدود 0.81 است.
نکته: با توجه به مقدار و مقایسه آن با که احتمال خطای نوع اول است، فرض صفر بودن پارامتر را رد میکنیم. در انتهای جدول در قسمت signif.codes، سطح معناداری یا همان مشخص شده است و در کنار مقدار آن نیز علامتی که به معنی معنادار بودن آزمون در سطح است دیده میشود. بنابراین از آنجایی که ضرایب متغیرهای wt و hp دارای علامت ** هستند، متوجه میشویم که در سطح خطای 0.01 فرض صفر بودن ضرایب رگرسیونی برای این متغیرها رد میشود.
به منظور تحلیل اثر هر یک از متغیرها مستقل در مدل و پیشبینی متغیر وابسته از تحلیل واریانس استفاده میشود. برای اجرای این تحلیل کافی است از دستور کمک بگیرید. به این ترتیب خروجی به صورت زیر درخواهد آمد.
1Analysis of Variance Table
2
3Response: mpg
4 Df Sum Sq Mean Sq F value Pr(>F)
5disp 1 808.89 808.89 119.4502 2.041e-11 ***
6hp 1 33.67 33.67 4.9714 0.034281 *
7drat 1 30.15 30.15 4.4519 0.044270 *
8wt 1 70.51 70.51 10.4121 0.003272 **
9Residuals 27 182.84 6.77
10---
11Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1به این ترتیب مشخص میشود که همه متغیرها در تغییر مقدار میانگین متغیر پاسخ (mpg) تاثیر دارند. به منظور بررسی صحت و ارزیابی مدل ارائه شده از لحاظ فرضیات رگرسیون خطی، رسم نمودارهایی که در ادامه خواهد آمد، بسیار کارا هستند.
نکته: توجه داشته باشید که برآورد مقدار خطا در مدل رگرسیونی همان اختلاف مقدار پیشبینی و مقدار واقعی است که در اینجا به آن «باقیمانده» (Residual) گفته میشود.
به کمک تابع میتوان چهار نمودار ترسیم کرد و از تفسیر آنها برای ارزیابی مدل استفاده کرد. این چهار نمودار در ادامه معرفی شدهاند.
- نمودار باقیمانده در مقابل مقدارهای پیشبینی شده.
- نمودار Q-Q plot که در آن چندکهای توزیع نرمال در مقابل باقیمانده استاندارد شده ترسیم میشود.
- ثابت بودن واریانس باقیماندهها با رسم مقدارهای پیشبینی شده در مقابل ریشه دوم باقیماندههای استاندارد
- رسم نمودار باقیمانده در مقابل میزان حساسیت مشاهدات که نقش هر مشاهده در صحت مدل رگرسیونی را نشان میدهد.
برای رسم این نمودارها کافی است دستور زیر را در خط فرمان Rstudio وارد کنید:
1plot(fit)ترتیب رسم نمودارها در این خروجی به همان ترتیبی است که آنها را معرفی کردیم. به این ترتیب ارزیابی مدل صورت گرفته و میتوان از آن به عنوان مدل پیشگو استفاده کرد.
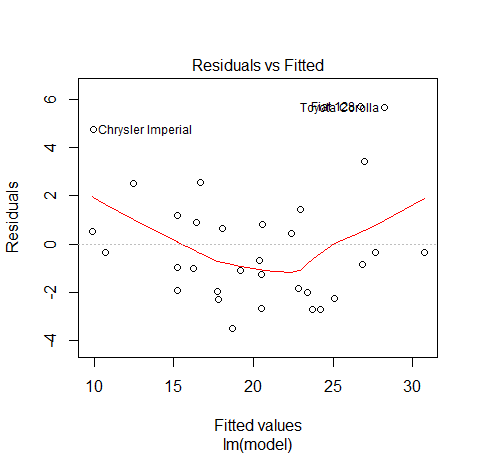
با توجه به روند تصادفی که مقدارهای پیشبینی و باقیماندهها دارند، مشخص است که باقیماندهها تصادفی حول میانگین صفر تغییر میکنند. پس فرضیه اول که تصادفی بودن و صفر بودن میانگین مقدارهای خطا بود، تایید میشود.
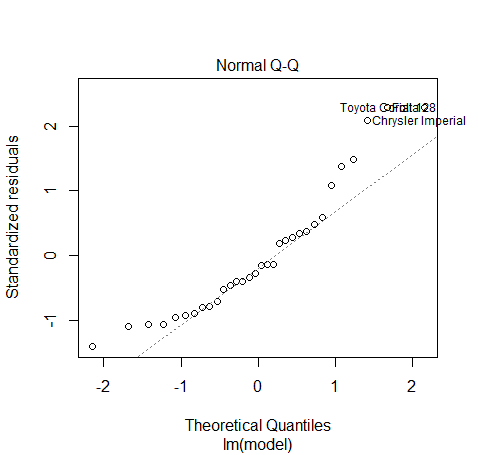
در این نمودار، چندکهای توزیع نرمال با چندکهای حاصل از باقیماندههای استاندارد شده ترسیم شده است. اگر توزیع باقیمانده مانند توزیع متغیر تصادفی نرمال باشد، نقطههای ترسیمی باید روی یک خط راست قرار گرفته باشند. همانطور که مشخص است به جز چند مورد خاص، بیشتر نقاط روی یک خط راست قرار گرفتهاند. پس میتوان نرمال بودن توزیع باقیماندهها در این حالت تایید کرد.
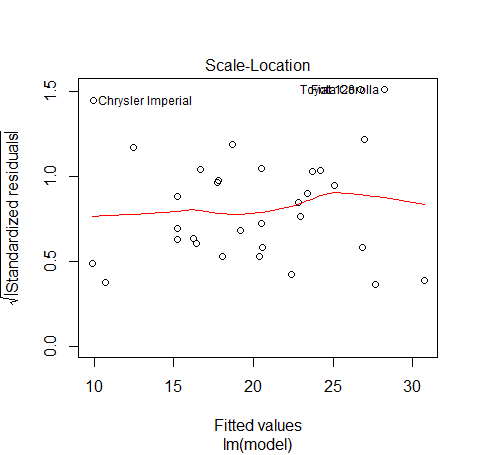
از طرفی واریانس باقیمانده نیز باید ثابت باشد. اگر نقطهها ترسیمی در این نمودار به صورتی بودند که به صورت یک قیف افقی ظاهر میشدند، مشخص میشد که بین واریانس باقیماندهها و با افزایش مقدار متغیر پیشبینی افزایش مییابد. در حالیکه این نمودار تقریبا ثابت بودن واریانس را نشان میدهد.
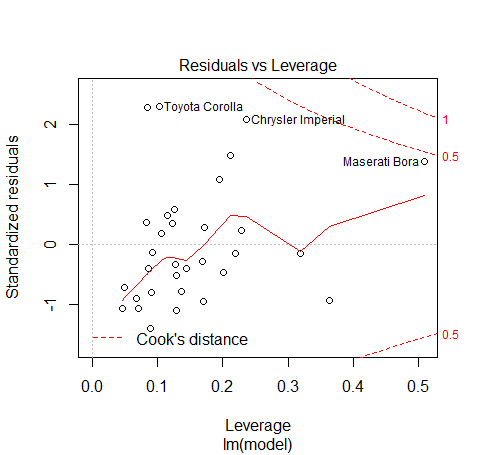
تحلیل حساسیت در این نمودار صورت گرفته است. مشخص است که نقاطی که دارای خطای بیش از بقیه هستند مربوط به تویوتا کرولا و کرایسلر و مازراتی است. برای سنجش فاصله بین نقطهها از فاصله کوک (Cook's distance) استفاده شده است. شاید با حذف این نقاط بتوان برآورد بهتر و با ضریب بزرگتر بدست آورد.
با رسم این نمودارها و خروجیهایی که توسط مدل رگرسیونی در R حاصل شد میتوان مدل پیشبینی را به صورت زیر نوشت:
با استفاده از این مدل مشخص میشود که برای تعیین مسافت طی شده برای هر خودرو بهتر است فقط از وزن و قدرت موتور آن استفاده کرد و طبق رابطه بالا عمل پیشبینی را انجام داد. برای مثال اگر خودروی دارای وزنی برابر با 3.9 (۱۰۰۰ پوند) و قدرت موتور 100 اسب بخار باشد، مسافتی که با یک گالن سوخت طی خواهد کرد برابر است با:
در نتیجه چنین خودرویی با یک گالن سوخت، حدود ۱۱ مایل طی خواهد کرد.
البته تابع متغیرهای دیگری نیز تولید میکند که به کمک دستورات زیر قابل دسترس هستند. برای مثال fit$coefficients، پارامترهای مدل را نمایش میدهد و fit$residuals نیز باقیمانده و fit$fitted.values نیز مقدارهای پیشبینی شده توسط مدل برای مشاهدات را نشان میدهد.
برای مشاهده قسمت دوم این متن به اینجا وارد شوید.
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزش های SPSS
- مجموعه آموزشهای نرمافزارهای آماری
- مجموعه آموزش های داده کاوی یا Data Mining در متلب
- آموزش همبستگی و رگرسیون خطی در SPSS
- مهمترین الگوریتمهای یادگیری ماشین (به همراه کدهای پایتون و R) — بخش دوم: رگرسیون خطی
- آموزش یادگیری ماشین
- رگرسیون لاسو (Lasso Regression) — به زبان ساده
- رگرسیون خطی با متغیرهای طبقه ای در SPSS — راهنمای گام به گام
- رگرسیون لجستیک (Logistic Regression) — مفاهیم، کاربردها و محاسبات در SPSS
^^













سلام.
روی این دادهها نمیتوان رگرسیون خطی درنظر گرفت زیرا متغیرها مستقل همبستگی دارند.