آزمون لون (Levene’s Test) برای برابری واریانس ها در SPSS – راهنمای کاربردی

در بیشتر موارد برای انجام آزمون‌های آماری مربوط به میانگین دو یا چند جامعه، توزیع آماره آزمون با فرض یکسان بودن واریانس آن‌ها مشخص می‌شود. بنابراین قبل از اجرای آزمون‌های میانگین، برابری واریانس‌ها در جوامع باید توسط «آزمون لون» (Levene's Test) بررسی شود. در این نوشتار به بررسی این آزمون و نحوه اجرای آن در SPSS می‌پردازیم. هرچند اجرای این آزمون به طور مستقل در SPSS امکان پذیر نیست ولی معمولا به همراه آزمون‌های آماری دیگر مانند آزمون t-test و یا ANOVA در SPSS قابل اجرا است.

به منظور آشنایی با آزمون‌های آماری  مطلب آزمون های فرض و استنباط آماری — مفاهیم و اصطلاحات را مطالعه کنید. همچنین خواندن متن آزمون فرض میانگین جامعه در آمار — به زبان ساده و تحلیل واریانس (Anova) — مفاهیم و کاربردها نیز خالی از لطف نیست.

آزمون لون (Leven's Test)

یکی از آماره‌های استنباطی برای سنجش برابری واریانس در چند جامعه مستقل، استفاده از آماره لون و اجرای آزمونی به نام «آزمون لون» (Levene's Test) است. در بیشتر نرم‌افزارهای آماری، محاسبه و اجرای این آزمون پیش‌زمینه‌ای برای آزمون‌های دیگر محسوب می‌شود.

برای مثال در آزمون مربوط به برابری میانگین دو جامعه مستقل، فرض برابری یا نابرابری واریانس‌ها، باعث ایجاد آماره‌های مجزا با درجه‌های آزادی متفاوت برای آزمون میانگین خواهد شد.

فرض صفر در آزمون لون، یکسان بودن واریانس‌ها است. بنابراین اگر $$\sigma^2_1$$ و $$\sigma_2^2$$ واریانس‌های دو جامعه مستقل باشند، فرض صفر برای این آزمون به صورت زیر نوشته خواهد شد.

$$\large \begin{cases}H_0: & \sigma^2_1 = \sigma^2_2\\\large H_1: & \sigma^2_1 \neq \sigma^2_2\end{cases}$$

آماره آزمون لون

فرض کنید از k گروه یا جامعه مستقل، نمونه‌گیری شده است. مشاهدات حاصل به صورت $$Y_{ij}$$ مشخص شده‌اند. اگر فاصله مشاهدات گروه i را از میانگین آن گروه که با $$\overline{Y}_i$$ نشان داده می‌شود با $$Z_{ij}$$ مشخص کنیم، آماره آزمون لون به صورت زیر محاسبه می‌شود.

$$\large W={\frac {(N-k)}{(k-1)}}\cdot {\frac {\sum _{i=1}^{k}N_{i}(Z_{i\cdot }-Z_{\cdot \cdot })^{2}}{\sum _{i=1}^{k}\sum _{j=1}^{N_{i}}(Z_{ij}-Z_{i\cdot })^{2}}}$$

ذکر این نکته نیز ضروری است که $$Z_{..}$$ میانگین کل گروه‌ها و $$Z_{i.}$$ نیز میانگین گروه iام را نشان می‌دهد. مشخص است که منظور از $$N$$ تعداد کل مشاهدات و $$N_i$$ نیز مشاهدات مربوط به گروه i است.

آماره $$W$$ به طور تقریبی دارای توزیع F با k-1 و N-k درجه آزادی است. بنابراین مقدار این آماره را باید با مقدار چندک $$\alpha$$ام توزیع F با این درجه‌های آزادی مقایسه کرد. اگر مقدار آماره $$W$$ بزرگتر از چندک توزیع F باشد، فرض صفر رد می‌شود.

$$\large W> F(\alpha;\;k-1,N-k), \;\;\; Reject\;\; H_0$$

نکته: معمولا مقدار $$\alpha$$ را برابر با 0.05 یا 0.01 در نظر می‌گیرند.

اگر از میانه به جای میانگین در آماره لون استفاده شود، آماره حاصل را «براون- فورسید» (Brown-Forsythe) و روش آزمون را «آزمون براون-فورسید» (Brown-Forsythe Test) می‌نامند. زمانی که داده‌ها دارای توزیع متقارن، بخصوص نرمال باشند، استفاده از آماره لون نتایج معتبر خواهد داشت در حالیکه برای داده‌هایی با توزیع‌های نامتقارن و دم سنگین مانند توزیع کای‌دو و کوشی، استفاده از میانه و آزمون «براون-فورسید» مناسب‌تر است.

اجرای آزمون لون در SPSS

برای اجرای آزمون لون، پیش‌فرض‌هایی نیز وجود دارد که در ادامه به آن‌ها اشاره کرده‌ایم.

• مشاهدات مستقل از یکدیگر باشند.
• داده‌ها از نوع کمی باشند.
• توزیع داده‌ها نرمال یا برای حجم داده حدود ۳۰، میزان چولگی اندک باشد.

در SPSS روش دسترسی مستقیم برای اجرای این آزمون وجود ندارد. در ادامه به 2 مورد از روش‌هایی که می‌توان در کنار آزمون‌های دیگر، آزمون لون را نیز انجام داد اشاره خواهیم کرد. همچنین با استفاده از چند مثال نتایج حاصل از این آزمون را مورد بررسی قرار می‌دهیم.

روش اول: آزمون مقایسه میانگین دو جامعه مستقل

برای دسترسی به آزمون میانگین دو جامعه مستقل در SPSS کافی است از فهرست Analysis گزینه Compare Means و دستور Independents-Sample T test را اجرا کنید. با توجه به شرایطی که آماره آزمون مقایسه میانگین‌ها دارد، SPSS دو حالت برای واریانس‌های این دو جامعه در نظر می‌گیرد. در حالتی که واریانس‌ها نامعلوم ولی برابر فرض شوند شیوه محاسبه آماره آزمون متفاوت با حالتی است که واریانس‌ها نابرابر باشند.

به همین منظور بطور خودکار SPSS ابتدا آزمون برابری واریانس‌ها (آزمون لون) را اجرا کرده، سپس نتایج آزمون مقایسه میانگین را در دو حالت برابری و نابرابری واریانس‌ها نشان می‌دهد. مراحل انجام این آزمون را با استفاده از این روش، با یک مثال ادامه می‌دهیم.

مثال ۱

فرض کنید داده‌هایی مربوط به وزن بسته‌های ماکارونی دو کارخانه در اختیارتان قرار گرفته است. متغیر مربوط به ستون اول، وزن و متغیر مربوط به ستون دوم مشخص کننده کارخانه تولید کننده است. از کارخانه اول نمونه ۲۰ تایی و از کارخانه دوم نیز نمونه ۱۸ تایی تهیه شده است. فایل فشرده مربوط به این داده‌ها را می‌توانید از اینجا دریافت کنید. با طی کردن مراحلی که در تصویر زیر می‌بینید، به آزمون مقایسه میانگین دو گروه مستقل دسترسی خواهید داشت.

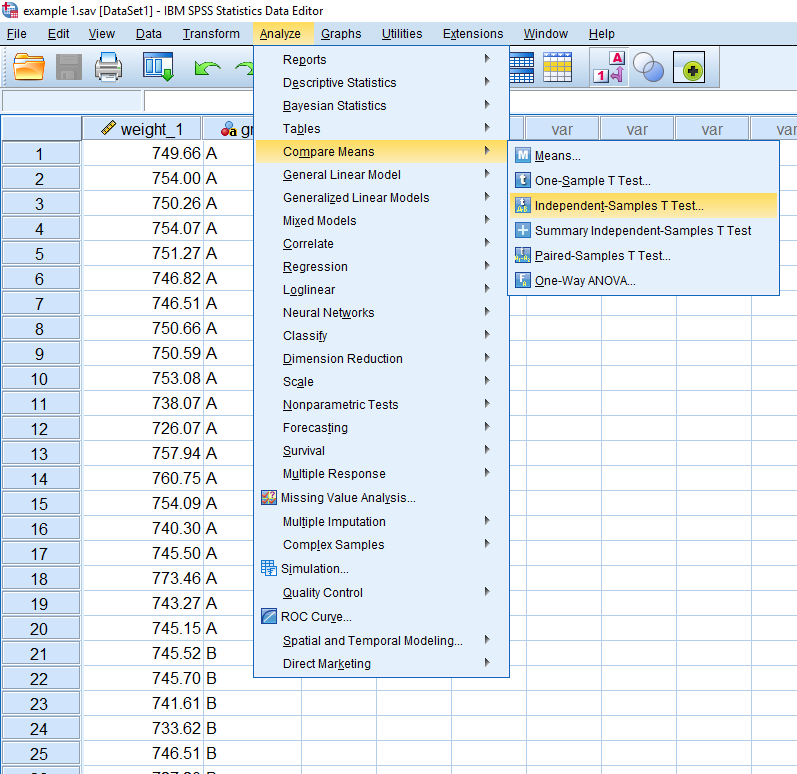
با اجرای این دستور، پنجره پارامترهای آزمون میانگین ظاهر می‌شود کافی است که پارامترها را به صورت زیر تکمیل کنید.

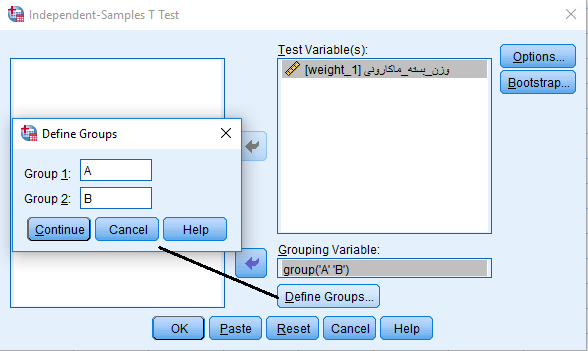
با اجرای این تنظیمات و فشردن دکمه OK، خروجی به صورت یک جدول ترکیبی از آزمون لون و آزمون میانگین T ظاهر خواهد شد. قسمت ابتدای این جدول به بررسی نتایج آزمون لون اختصاص دارد. همانطور که دیده می‌شود، مقدار Sig که همان p-value است، بزرگتر از سطح خطای آزمون $$\alpha=0.05$$ است در نتیجه فرض برابر بودن واریانس دو جامعه رد نمی‌شود.

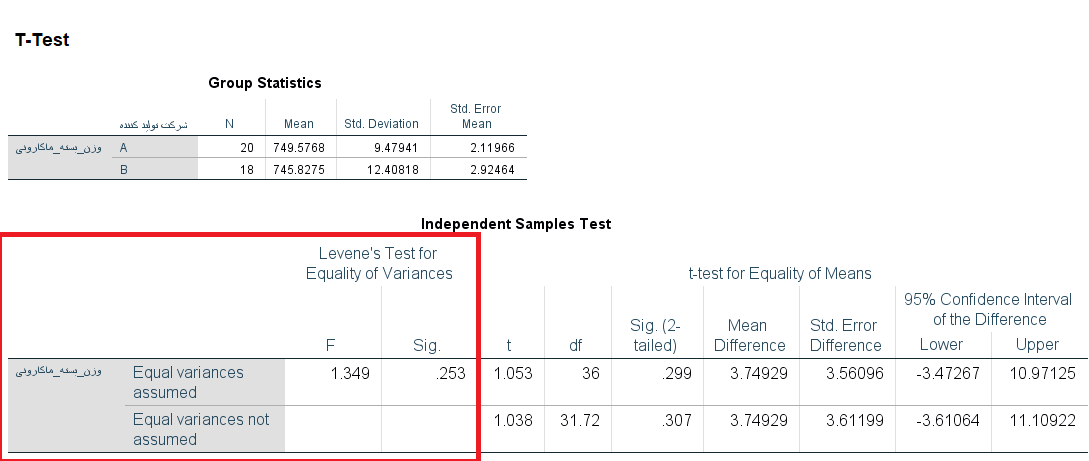
روش دوم: آزمون مقایسه میانگین چند جامعه مستقل (ANOVA)

در این قسمت نیز با استفاده از یک مثال، به بررسی دسترسی به آزمون لون از طریق تحلیل واریانس یا ANOVA می‌پردازیم. با توجه به اینکه در تحلیل واریانس، تعداد گروه‌ها بیشتر از ۲ هستند، مقایسه بین واریانس چندین جامعه توسط آزمون لون مورد بررسی قرار می‌گیرد.

فیلم آموزش رایگان اس پی اس اس SPSS – سریع و آسان در ۱۱۰ دقیقه + گواهینامه در فرادرس

کلیک کنید

در این حالت فرضیات آزمون به صورت زیر نوشته خواهند شد.

$$\large \begin{cases}H_0: & \sigma^2_1 = \sigma^2_2 =\cdots =\sigma^2_k \\\large H_1: & \text{Not}\;\; H_0\end{cases}$$

در اینجا فرض مقابل یا $$H_1$$ بیان می‌کند که تساوی واریانس‌ها در حداقل بین دو گروه یا جامعه برقرار نیست.

مثال ۲

همگام با مثال ۱، فرض کنید قرار است میانگین وزن تولیدات سه بسته ماکارونی ۷۵۰ گرمی از سه کارخانه با یکدیگر مقایسه شود. فایل مربوط به این داده‌ها نیز در اینجا قابل دریافت است. برای اجرای تحلیل واریانس یا ANOVA در SPSS باید از مسیر Analysis گزینه Compare means و دستور One-way ANOVA را اجرا کنید.

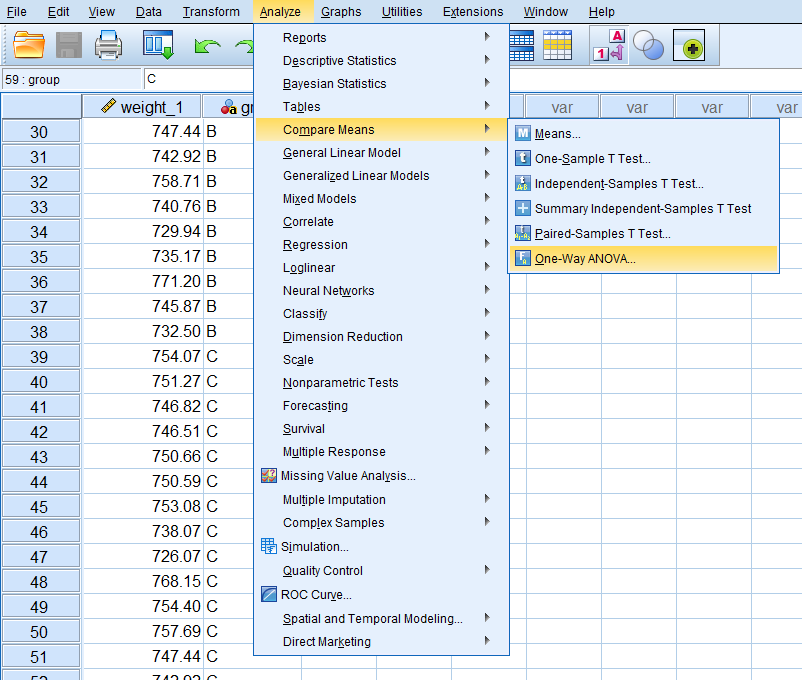
نکته: یکی از خصوصیات دستور ANOVA این است که متغیری که نشانگر گروه یا جامعه‌ها است باید عددی باشد. از آنجایی که در اینجا متغیر group متنی است باید بوسیله روش کدگذاری خودکار Automatic Recode مقدارهای متنی A و B و C را به اعداد ۱ و ۲و ۳ تبدیل کنیم. تنظیمات مربوط به نحوه اجرای Automatic Recode از فهرست Transform در تصویر زیر دیده می‌شود.

با این کار متغیر جدیدی به نام group_numeric ساخته شده که مبنای شناسایی جامعه‌ها در «تحلیل واریانس» (ANOVA) قرار خواهد گرفت.

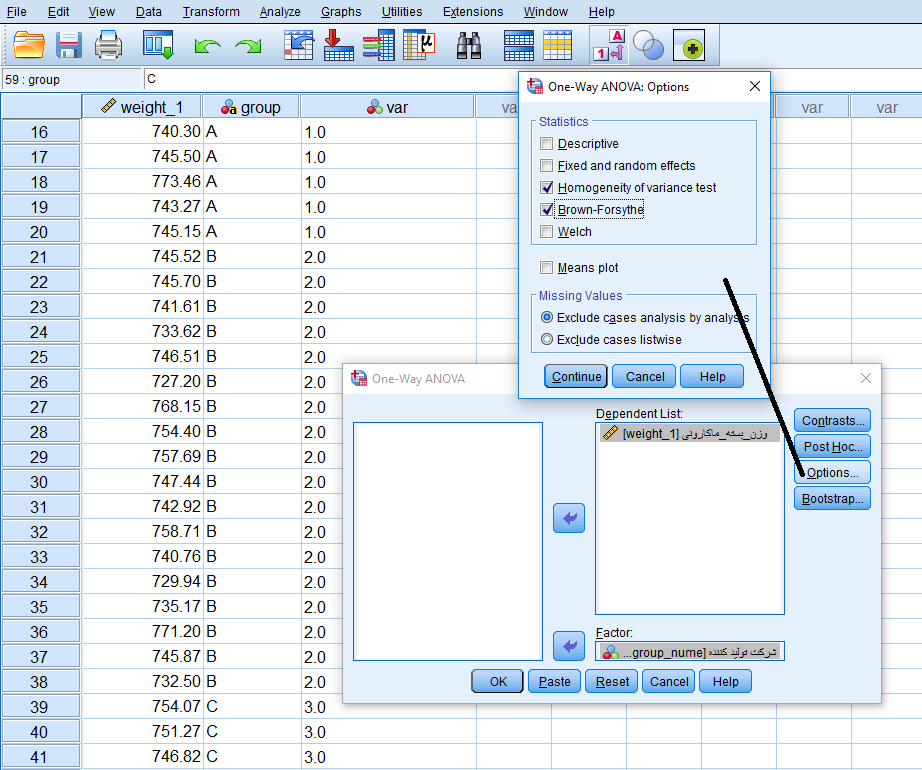
همانطور که دیده می‌شود با فشردن دکمه Options گزینه‌های مربوط به اجرای «آزمون لون» (Homogeneity of variance test) و همچنین «آزمون براون-فورسید» (Brown-Forsythe) قابل انتخاب است. با گزینش آن‌ها و اجرای آزمون، خروجی به صورت زیر دیده خواهد شد.

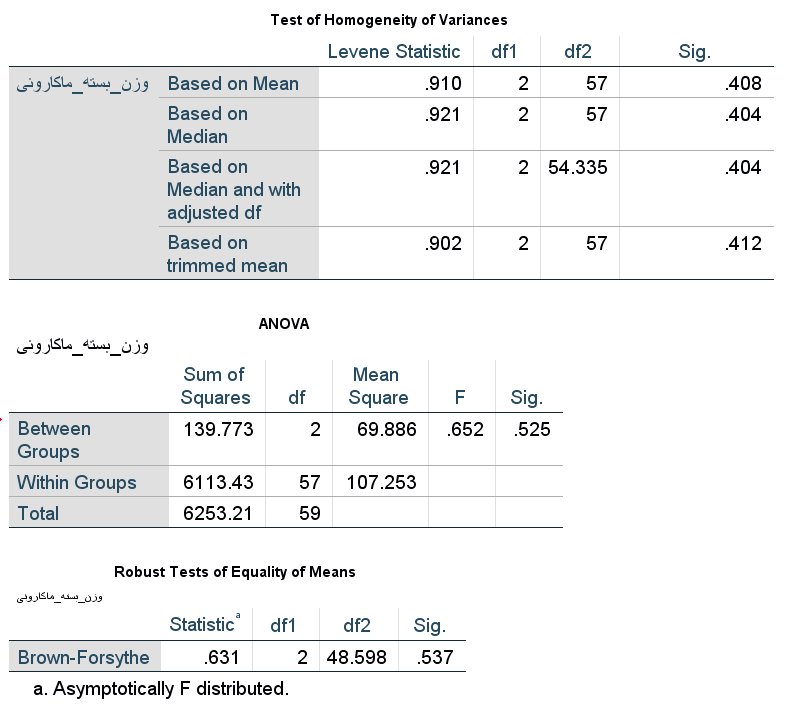
با توجه به خروجی جدول اول و سوم در قسمت Sig مشخص است که فرض برابری واریانس وزن بسته‌های ماکارونی در بین این سه کارخانه رد نمی‌شود، زیرا همه این مقدار Sigها از سطح خطای آزمون 0.05 بزرگتر هستند. پس نمونه دلیل برای رد فرض صفر ارائه نمی‌دهد.

اگر به فراگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های SPSS
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آزمایش تصادفی، پیشامد و تابع احتمال
• مجموعه آموزش‌های نرم‌افزارهای آماری
• آموزش آزمون های فرض مربوط به میانگین جامعه نرمال در SPSS
• آموزش آزمون آماری و پی مقدار (p-value)
• جامعه آماری — انواع داده و مقیاس‌های آن‌ها
•  تحلیل‌ها و آزمون‌های آماری — مفاهیم و اصطلاحات

^^