فرادرسمتغیر تصادفی و توزیع کای ۲ (Chi Squared) — مفاهیم و کاربردها
شناخت توزیع احتمال برای پدیده‌های تصادفی، پیش‌بینی رخداد پیشامدها را امکان‌پذیر می‌سازد. یکی از توزیع‌های مهم آماری، «توزیع کای۲» (Chi Squared Distribution) است که بخصوص در آزمون نیکویی برازش به کار می‌رود. در این نوشتار به بررسی این توزیع آماری می‌پردازیم.
اولین بار این توزیع توسط دانشمند آلمانی آمار «رابرت هلمرت» (Robert Helmert) در مقاله‌ای در سال 1875 معرفی شد. ولی بعدها «کارل پیرسن» (Karl Pearson) از آن برای انجام آزمون‌های برازش استفاده کرد. هرچند نام «کای۲» (Chi Squared) را آماردان بزرگ «رونالد فیشر» (Ronald Fisher) در سال ۱۹۲۰ برای آن انتخاب کرد. این توزیع را گاهی با نام‌های «کای مربع»، «خی ۲» یا «خی اسکور» نیز به کار می‌برند.
به عنوان مقدمات برای این نوشتار، بهتر است ابتدا مطلب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال را مطالعه کرده باشید. همچنین مطالعه مطلب مربوط به توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها و توزیع های آماری گاما و بتا — مفاهیم و کاربردها نیز خالی از لطف نیست.
متغیر تصادفی و توزیع کای ۲
متغیر تصادفی و توزیع کای۲ کاربردهای زیادی بخصوص در آزمون‌های نیکویی برازش و همچنین آزمون استقلال متغیرهای کیفی دارد. فرض کنید $$Z_1, Z_2,\cdots, Z_k$$ تعداد k متغیر تصادفی نرمال استاندارد مستقل باشند.
آنگاه جمع مربعات این متغیرهای تصادفی دارای توزیع کای۲ است. در این حالت داریم:
$$\large \displaystyle Q\ =\sum _{i=1}^{k}Z_{i}^{2}$$
به این ترتیب می‌نویسم $$Q\sim \chi^2_k$$ و می‌خوانیم، Q دارای توزیع کای۲ با k درجه آزادی است. مشخص است که این توزیع دارای یک پارامتر به نام «درجه آزادی» (Degree of Freedom) است که مقدار آن مثبت است. گاهی درجه آزادی را با df نیز نشان می‌دهند.
تابع چگالی توزیع کای ۲
اگر X یک متغیر تصادفی با توزیع کای۲ باشد، آنگاه تابع چگالی احتمال برای آن به صورت زیر خواهد بود.
$$\large \displaystyle f_X(x;\,k)={\begin{cases}{\dfrac {x^{{\frac {k}{2}}-1}e^{-{\frac {x}{2}}}}{2^{\frac {k}{2}}\Gamma \left({\frac {k}{2}}\right)}},&x>0;\\0,&{\text{otherwise}}.\end{cases}}$$
مشخص است که عبارت $$\Gamma(\frac{k}{2})$$ مقدار تابع گاما در نقطه $$\frac{k}{2}$$ است. تصویر زیر، نمودار مربوط به تابع چگالی احتمال (Probability Density Function- pdf) این توزیع را برای مقدارهای مختلف k نشان می‌دهد.
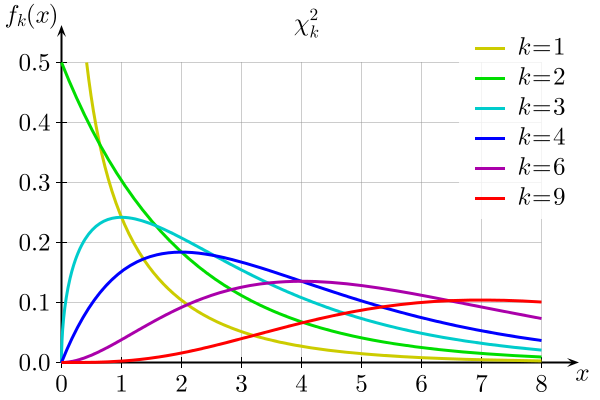
براساس نمودار مشخص است که تکیه‌گاه این متغیر تصادفی، مجموعه اعداد حقیقی مثبت به ازای k=۱ و برای بقیه مقدارهای k، تکیه‌گاه مجموعه اعداد حقیقی نامنفی است. به این ترتیب می‌توان نوشت:
$$\large \displaystyle S={\begin{cases} (0,\infty) &k=1\\ [0,\infty),&k>1 .\end{cases}}$$
همانطور که در نمودار دیده می‌شود، این توزیع، نامتقارن و چوله به راست است. با افزایش مقدار درجه آزادی (k)، چولگی کاهش یافته و نمودار تابع احتمال به صورت یک نمودار متقارن درخواهد آمد. همچنین با توجه به قضیه حد مرکزی، می‌توان نتیجه گرفت که با افزایش k، این توزیع به سمت نرمال میل خواهد کرد.
تابع توزیع احتمال تجمعی
همانطور که از مطالب قبلی فرادرس در مورد تابع توزیع احتمال و تابع توزیع احتمال تجمعی خوانده‌اید، می‌دانید که برای بدست آوردن تابع توزیع احتمال تجمعی برای متغیرهای تصادفی پیوسته در نقطه y باید انتگرال تابع توزیع احتمال را از ۰ تا نقطه y محاسبه کرد. در نتیجه برای محاسبه تابع توزیع احتمال تجمعی متغیر تصادفی کای۲ خواهیم داشت:
$$\large \displaystyle F_X(y;\,k)=\int_0^y {\dfrac {x^{{\frac {k}{2}}-1}e^{-{\frac {x}{2}}}}{2^{\frac {k}{2}}\Gamma \left({\frac {k}{2}}\right)}}dx$$
البته حاصل این انتگرال را به کمک تابع «گامای ناکامل» (Incomplete Gamma Function) نیز می‌توان نشان داد. در این صورت می‌توان نوشت:
$$\large \displaystyle F_X(y;\,k)=\frac {\gamma ({\frac {k}{2}},\,{\frac {x}{2}})}{\Gamma ({\frac {k}{2}})}$$
مشخص است که در اینجا منظور از $${\gamma ({\frac {k}{2}},\,\frac {x}{2})}$$، همان مقدار تابع گامای ناکامل در نقطه‌های $$\frac{k}{2}$$ و $$\frac{x}{2}$$ است که در زیر شیوه محاسبه آن آورده شده است.
$$\large \displaystyle \gamma (s,x)=\int _{0}^{x}t^{s-1}\,e^{-t}\,{\rm {d}}t$$
نکته: در حالت خاص که k=2 باشد، تابع توزیع احتمال تجمعی متغیر تصادفی کای۲، به شکل ساده‌تری در می‌آید که در ادامه دیده می‌شود.
$$\large \displaystyle F(x;\,2)=1-e^{-x/2}$$
به کمک جدول‌های تابع توزیع احتمال تجمعی متغیر تصادفی کای۲ که از قبل تهیه شده‌اند، محاسبه احتمال برای پیشامدهایی با این توزیع احتمالی به راحتی امکان‌پذیر است. در زیر به یک نمونه از این جدول‌ها اشاره شده است.
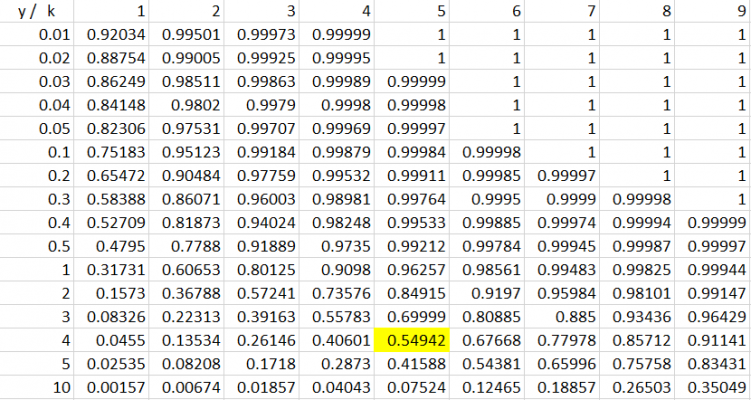
در سطر اول این جدول، مقدار درجه آزادی و در ستون اول نیز مقدار y ثبت شده است. مقدارهایی درون جدول نیز تابع احتمال تجمعی را در نقطه y نشان می‌دهند. برای مثال فرض کنید بخواهیم مقدار احتمال را تا نقطه 4 برای متغیر تصادفی $$X\sim \chi^2_5$$ (توزیع کای۲ با ۵ درجه آزادی) محاسبه کنیم. طبق جدول داریم.
$$F_X(y=4)=P(X\leq 4)=0.54942$$
از آنجایی که در آزمون‌های آماری مربوط به این توزیع، احتیاج به صدک‌ها داریم، جدول‌هایی نیز برای محاسبه آن تهیه شده که در تصویر زیر یک نمونه از آن را می‌بینید.
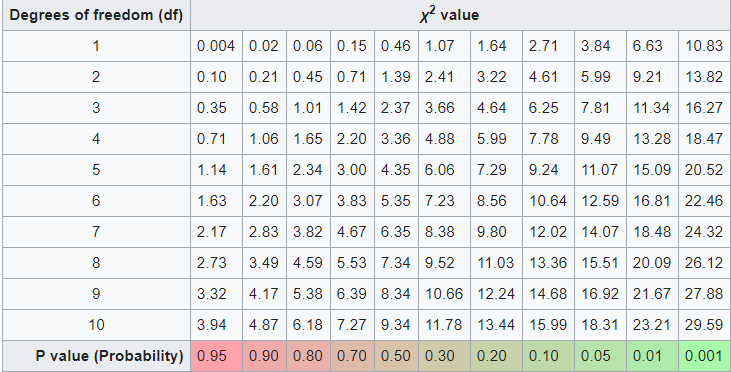
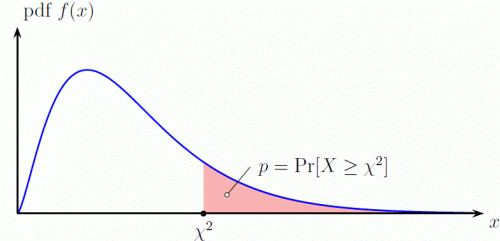
باید توجه داشت که در این جدول صدک‌های بالایی مربوط به توزیع کای۲ محاسبه شده است. منظور از صدک بالایی در اینجا مقدار p است که به صورت $$ p=P(X\geq \chi^2\; value)$$ بدست می‌آید.
در ستون اول این جدول، درجه آزادی (df) و در سطر آخر نیز درصد مربوط به صدک‌های بالایی دیده می‌شود. مقدارهایی که در محل تقاطع سطر و ستون جدول دیده می‌شود، مقدار صدک بالایی مربوط به توزیع کای ۲ به ازاء درجه آزادی آن سطر و درصد آن ستون است.
برای مثال اگر لازم است که مقدار صدک 95ام (یا صدک ۵ام بالایی) از توزیع کای۲ با ۱۰ درجه آزادی مشخص شود، از سطر آخر ستون مربوط به مقدار 0.95 را انتخاب کرده و مقدار مربوط به درجه آزادی (df=10) را می‌خوانیم که در اینجا برابر با 18.31 است. این نقطه، مقداری از متغیر تصادفی توزیع کای۲ را نشان می‌دهد که احتمال تا آن نقطه برابر با ۹۵٪ یا احتمال از آن نقطه به بعد برابر با 0.05 است.
خصوصیات توزیع کای ۲
با توجه به رابطه‌ای که بین مجموع مربعات متغیر تصادفی نرمال استاندارد و متغیر تصادفی کای۲ وجود دارد، می‌توان خصوصیات زیر را برای این توزیع در نظر گرفت.
امید ریاضی و واریانس
مشخص است که واریانس متغیرهای تصادفی $$Z_i$$ها همان امید ریاضی $$Z^2_i$$ است. همینطور می‌دانیم که این متغیرهای تصادفی، مستقل نیز هستند. پس امید ریاضی برای جمع $$Z^2_i$$ها برابر با k است. در نتیجه خواهیم داشت:
$$\large E(\chi^2)=E(\sum_{i=1}^k Z^2_i)=\sum_{i=1}^k Var(Z_i)=k$$
به همین ترتیب نیز می‌توان واریانس را برای متغیر تصادفی کای۲ محاسبه کرد. در این حالت خواهیم داشت:
$$\large Var(\chi^2)=2k$$
برای مثال امید ریاضی و واریانس یک متغیر تصادفی کای۲ با ۴ درجه آزادی به ترتیب برابر با ۴ و ۸ خواهد بود.
رابطه با توزیع‌های دیگر
از آنجایی که توزیع کای۲ براساس توزیع نرمال استاندارد ساخته شده است، خصوصیات مطلوب و جالبی دارد. در این قسمت به بررسی خصوصیات این توزیع نسبت به توزیع‌های دیگر می‌پردازیم.
اگر $$X_1, X_2, \cdots X_n$$ متغیرهای تصادفی مستقل با توزیع کای۲ با درجه‌های آزادی $$k_1, k_2, \cdots k_n$$ باشند، جمع آن‌ها نیز دارای توزیع کای۲ با درجه آزادی جمع kها خواهد بود. در نتیجه می‌توان نوشت:
$$X=(X_1+X_2+\cdots+X_n)\sim \chi^2_{(k_1+k_2+\cdots+k_n)}$$
به همین ترتیب می‌توان میانگین این متغیرهای تصادفی را توزیع گاما با پارامتر شکل $$\kappa=\frac{nk}{2}$$ و پارامتر مقیاس $$\theta=\frac{2}{n}$$ دانست. به این ترتیب داریم.
$$\large \displaystyle {\bar {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}\sim \operatorname {Gamma} \left(\kappa=\frac{n}{2},\theta =\frac{2}{n}\right)$$
از طرفی می‌توان دید که توزیع کای۲ با k درجه آزادی (k صحیح) را می‌توان همان توزیع گاما با پارامترهای $$\alpha=\frac{n}{2}$$ و $$\beta=\frac{1}{2}$$ در نظر گرفت. همچنین می‌توان نشان داد که توزیع کای۲ با ۲ درجه آزادی، همان توزیع نمایی با پارامتر $$\frac{1}{2}$$ است.
یکی از مهم‌ترین رابطه‌هایی که بخصوص در آزمون‌های فرض مربوط به واریانس و آماره آزمون آن به کار گرفته می‌شود، رابطه‌ای است که بین برآورد واریانس یعنی $$S^2$$ و واریانس جامعه $$\sigma^2$$ وجود دارد. حاصل ضرب این نسبت با n-1 دارای توزیع کای۲ است. بنابراین می‌توان نوشت:
$$\large \displaystyle \dfrac{(n-1)S^2}{\sigma^2}\sim \chi^2_{(n-1)}$$
به شرطی که $$S^2=\dfrac{1}{n-1}\sum_{i=1}^n(X_i-\bar{X})^2$$ محاسبه شود. در نتیجه این رابطه می‌تواند یک آماره آزمون با تابع محوری برای ایجاد فاصله اطمینان تلقی شود زیرا برحسب پارامتر مجهول است ولی توزیع آن به پارامتر مجهول بستگی ندارد.
اگر به فراگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
- آزمایش تصادفی، پیشامد و تابع احتمال
- مجموعه آموزش‌های SPSS
- آموزش آمار و احتمال مهندسی
- مجموعه آموزش‌های نرم‌افزارهای آماری
- جامعه آماری — انواع داده و مقیاس‌های آن‌ها
- تحلیل‌ها و آزمون‌های آماری — مفاهیم و اصطلاحات
- فاصله اطمینان (Confidence Interval) — به زبان ساده
^^
سلام خسته نباشید . عالی بود . فقط لطفا برای هر مبحث مثال های بیشتری قرار دهید