دسته بند بیز ساده و داده های استاندارد شده — پیاده سازی در پایتون

«تغییر مقیاس» (Re-scaling) و «تبدیل» (Transformation) یکی از بخشهای اصلی کار بر روی دادهها به منظور انجام «تحلیلهای آماری» (Statistical Analysis) و «مدلسازی» (Modeling) محسوب میشود که در فرآیند «دادهکاوی» (Data Mining) در بخش «آمادهسازی دادهها» (Data Preparation) صورت میگیرد. این کار زمانی که به «تحلیل چند متغیره» (Multivariate Analysis) مشغول هستید، بسیار ضروری است، زیرا ممکن است دادههای با مقیاس بزرگتر نقش بیشتری در مدلسازی داشته باشند چون واریانس بزرگتری نیز خواهند داشت. ولی اگر دادههای مربوط به متغیرها را بدون واحد یا به شکلی با یک واحد اندازهگیری نشان داده و به کار بریم، بهتر میتوانیم اهمیت هر یک را در تعیین مدل مشخص کنیم. در این نوشتار به بررسی یک روش تبدیل به نام «استانداردسازی» (Standardization) و نقش آن در تکنیک «تحلیل مولفههای اصلی» (Principal Component Analysis- PCA) و «دسته بند بیز ساده» (Naive Bayes Classifier) میپردازیم. برای انجام محاسبات و مدلسازی نیز از کدهایی در زبان برنامه نویسی پایتون استفاده خواهیم کرد.
برای آشنایی بیشتر با نحوه انجام تبدیل استاندارد سازی بهتر است مطلب استاندارد سازی و نرمال سازی دادهها در پایتون — تفاوت و شباهتها را مطالعه کنید. البته خواندن نوشتار تحلیل مولفه اساسی (PCA) — راهنمای عملی به همراه کد نویسی در پایتون و R و الگوریتم بیز ساده در پایتون — راهنمای کاربردی نیز خالی از لطف نیست.
دسته بند بیز ساده و دادههای استاندارد شده
بسیاری از روشها و تکنیکهای آماری که در حوزه «تحلیل چند متغیره» (Multivariate Analysis) قرار دارند، احتیاج به استانداردسازی یا نرمالسازی داده دارند تا به این وسیله متغیرهای با اهمیت، شناسایی شده و به شکلی، مدل بدون در نظر گرفتن مقیاس یا واحد اندازهگیری مقادیر، ایجاد شود. در این نوشتار به بررسی «دستهبند بیز ساده» (Naive Bayes Classifier) خواهیم پرداخت که از طرفی به عنوان یک ابزار «یادگیری ماشین» (Machine Learning) بوده و با توجه به استفاده از چند ویژگی میتوان آن را تحلیل چند متغیره نیز در نظر گرفت.
از سوی دیگر به منظور کاهش ابعاد یک مسئله پیچیده چند متغیره، روشهای مختلفی مانند «تحلیل مولفههای اصلی» (Principcal Component Analysis- PCA) و «تحلیل تشخیص خطی» (Linear Discriminant Analysis- LDA) وجود دارند که متاسفانه به واحد اندازهگیری دادهها بسیار حساس هستند. در این نوشتار سعی میکنیم از تاثیر استفاده از تبدیلاتی مانند استانداردسازی بر روی تحلیل مولفههای اصلی و همچنین به کارگیری دستهبند بیز ساده آشنا شده و نتایج دقت در تشخیص گروهها را به کمک مثالی مورد بررسی قرار دهیم. این متن شامل چندین قسمت است که در هر بخش یکی از گامهای تحلیل دستهبند بیز ساده صورت میپذیرد. این مراحل و گامها در ادامه فهرست شدهاند.
- گام اول: خواندن و بارگذاری دادهها و تفکیک آنها به دو بخش «دادههای آموزشی» (Training Set) و «دادههای آزمایشی» (Test Data)
- گام دوم: استاندارد کردن دادهها و ویژگیها (متغیرهای عددی)
- گام سوم: استفاده از تحلیل مولفههای اصلی (PCA) به منظور کاهش بعد مسئله
- گام چهارم: به کارگیری دستهبندی بیز ساده (Naive Bayes Classifier) روی دادههای آموزشی
- گام پنجم: بررسی دقت دستهبندی دادههای اصلی و استاندارد شده
گام اول: خواندن دادهها و تفکیک به بخش آموزشی و آزمایشی
در این نوشتار از یک مجموعه داده استفاده شده است که براساس یک متغیر کیفی یا طبقهای مشاهدات را به ۳ گروه تقسیم کرده است. متغیرهای کمی دیگر شامل ۱۳ ویژگی عددی هستند که مرتبط با این دسته یا گروهها در نظر گرفته میشوند. از آنجایی که ممکن است بعضی از این متغیرها با یکدیگر همبستگی داشته باشند و باعث ایجاد «بیشبرازش» (Overfitting) در مدل شوند، میخواهیم آنها را با استفاده از تکنیک PCA به مولفهها یا متغیرهای جدیدی که کمترین وابستگی را دارند تفکیک کنیم، بطوری که بیشترین تغییرات (واریانس) را در خود حفظ کنند. از طرفی برای تنظیم پارامترهای مدل و تعیین دقت دستهبندی، دادهها را به دو بخش آموزشی و آزمایشی تفکیک خواهیم کرد. کدی که در ادامه مشاهده میکنید به منظور فراخوانی این مجموعه داده از اینترنت و تفکیک آن به دو بخش ذکر شده، مورد استفاده قرار میگیرد.
1import pandas as pd
2
3df = pd.io.parsers.read_csv(
4 'https://raw.githubusercontent.com/rasbt/pattern_classification/master/data/wine_data.csv',
5 header=None,
6 )
7from sklearn.cross_validation import train_test_split
8
9X_wine = df.values[:,1:]
10y_wine = df.values[:,0]
11
12X_train, X_test, y_train, y_test = train_test_split(X_wine, y_wine,
13 test_size=0.30, random_state=12345)همانطور که مشخص است ۷۰٪ دادهها به گروه آموزشی و ۳۰٪ نیز به گروه آزمایشی تعلق دارند. برای انجام این کار از کتابخانه sklearn و تابع train_test_split از گروه cross_validation استفاده شده است.
گام دوم: استاندارد کردن دادهها و ویژگیها
از آنجایی که هر یک از این دادهها دارای مقیاس اندازهگیری متفاوتی هستند، لازم است که مقیاس اندازهگیری را از بین ببریم. در این میان از شیوه استانداردسازی z-score استفاده میشود که دادهها را به شکلی در میآورد که دارای میانگین صفر و واریانس واحد (یک) شوند. کدی که در ادامه میبینید این محاسبات را بر روی دادههای آموزشی و آزمایشی انجام داده است.
1from sklearn import preprocessing
2
3std_scale = preprocessing.StandardScaler().fit(X_train)
4X_train_std = std_scale.transform(X_train)
5X_test_std = std_scale.transform(X_test)
6
7print(std_scale)
8print(X_train_std)
9print(X_test_std)قسمتی از خروجی این دستور در ادامه قابل مشاهده است.
1StandardScaler(copy=True, with_mean=True, with_std=True)
2[[-1.87897935 1.16139809 -1.95836639 ..., -0.97692884 0.30321156
3 -0.54967345]
4 [-0.75525649 -1.08867904 -0.91454568 ..., 0.28222389 0.24180162
5 -0.25245748]
6 [-0.36010119 -0.7010253 -0.3180767 ..., -0.06512859 -0.84822474
7 -0.75287213]
8 ...,
9 [ 0.98589652 0.33552709 -0.16895946 ..., -1.19402414 -1.43161913
10 -0.3889342 ]
11 [-1.16276038 1.63332438 0.12927503 ..., -0.8032526 -0.06524806
12 -0.49508276]
13 [ 1.28226299 -0.57461647 -0.50447326 ..., 0.28222389 1.50070531
14 0.88484854]]
15.........
16 [ -9.03439723e-01 -5.32480196e-01 -8.39987058e-01 -1.30475192e-01
17 -1.30408027e+00 -9.79798183e-01 4.04427076e-02 8.17196236e-02
18 9.91570100e-02 -6.49076749e-01 1.08547649e-01 8.55900981e-01
19 -7.07379888e-01]
20 [ 8.13016082e-01 6.22053763e-01 8.00302630e-01 -1.22248071e+00
21 1.32766219e+00 6.80185206e-01 1.07019543e+00 -1.52673011e+00
22 1.49964734e-01 1.25435758e-01 -6.51285896e-02 1.14759818e+00
23 3.08613493e-01]
24 [ -6.93513473e-01 -6.33607258e-01 -5.79031881e-01 8.75319361e-01
25 7.42830532e-01 -4.26470387e-01 1.02227871e-01 -1.59547837e-01
26 6.52851939e-02 -1.25957484e+00 3.69062008e-01 5.33498818e-01
27 -1.20779454e+00]
28 [ -5.82376047e-01 -9.45415699e-01 -3.55356014e-01 -5.61530000e-01
29 -9.38560481e-01 -4.26470387e-01 -1.45269873e+00 1.93143682e+00
30 -5.44407495e-01 2.84894215e-01 -9.76928844e-01 -1.69261136e+00
31 -2.82785640e-01]
32 [ 1.52923505e+00 -5.57761961e-01 -1.68959458e-01 -9.06373847e-01
33 1.47387010e+00 1.47065349e+00 1.03930284e+00 -8.02927731e-01
34 7.76593331e-01 7.08598116e-01 -1.51966709e-01 1.07083576e+00
35 6.87715500e-01]]کاملا مشخص است که دادهها در فاصله قرار گرفتهاند.
گام سوم: تحلیل مولفههای اصلی (PCA) به منظور کاهش بعد مسئله
در این قسمت تکنیک PCA را روی دادههای آموزشی استاندارد شده و البته استاندارد نشده (دادههای اصلی) اجرا میکنیم تا در گامهای بعدی بتوانیم در مورد دقت دستهبند بیز برای هر دو گروه داده، مقایسهای صورت دهیم. دو مولفه اول را پس از اجرای دستور PCA انتخاب و از آنها در الگوریتم دستهبندی بیز ساده استفاده خواهیم کرد.
نکته: اغلب برای تعیین ویژگیهای مهم در مدلسازی از تکنیکهای مختلف از جمله «اعتبارسنجی متقابل» (Cross Validation) استفاده میشود. ولی در اینجا به دنبال مقایسه صحت دستهبندی برای دادههای استاندار شده و اصلی هستیم و از انجام این کار صرفنظر میکنیم.
کدی که در زیر مشاهده میکنید به منظور استخراج مولفههای اصلی برای این مجموعه داده تهیه شده است.
1from sklearn.decomposition import PCA
2
3# on non-standardized data
4pca = PCA(n_components=2).fit(X_train)
5X_train = pca.transform(X_train)
6X_test = pca.transform(X_test)
7
8
9# om standardized data
10pca_std = PCA(n_components=2).fit(X_train_std)
11X_train_std = pca_std.transform(X_train_std)
12X_test_std = pca_std.transform(X_test_std)همانطور که گفته شد قرار است از دو مولفه اصلی استفاده شود، بنابراین میتوانیم پراکندگی مربوط به نقاط حاصل از مولفهها را روی محور مختصات دکارتی نمایش دهیم. نموداری که توسط کد زیر تولید شده به این منظور ترسیم خواهد شد.
1from matplotlib import pyplot as plt
2
3fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(10,4))
4
5
6for l,c,m in zip(range(1,4), ('blue', 'red', 'green'), ('^', 's', 'o')):
7 ax1.scatter(X_train[y_train==l, 0], X_train[y_train==l, 1],
8 color=c,
9 label='class %s' %l,
10 alpha=0.5,
11 marker=m
12 )
13
14for l,c,m in zip(range(1,4), ('blue', 'red', 'green'), ('^', 's', 'o')):
15 ax2.scatter(X_train_std[y_train==l, 0], X_train_std[y_train==l, 1],
16 color=c,
17 label='class %s' %l,
18 alpha=0.5,
19 marker=m
20 )
21
22ax1.set_title('Transformed NON-standardized training dataset after PCA')
23ax2.set_title('Transformed standardized training dataset after PCA')
24
25for ax in (ax1, ax2):
26
27 ax.set_xlabel('1st principal component')
28 ax.set_ylabel('2nd principal component')
29 ax.legend(loc='upper right')
30 ax.grid()
31plt.tight_layout()
32
33plt.show()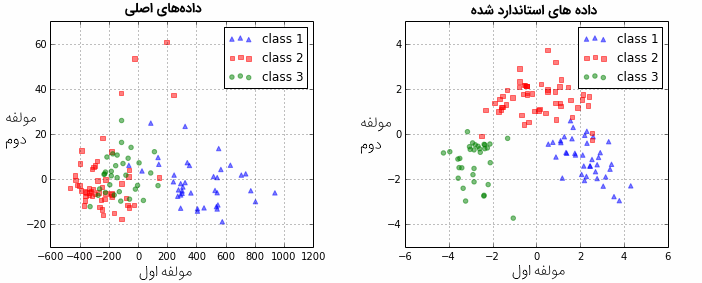
گام چهارم: به کارگیری دستهبندی بیز ساده روی دادههای آموزشی
در این مرحله به منظور دستهبندی دادههای اصلی و استاندارد شده به سه گروه، از الگوریتم «دستهبند بیز ساده» (Naive Bayes Classifier) بهره میبریم. همانطور که در نوشتار دسته بند بیز ساده (Naive Bayes Classifiers) — مفاهیم اولیه و کاربردها قابل مشاهده است، این تکنیک از قضیه بیز استفاده میکند. به منظور یادآوری این قضیه و چگونگی استفاده از آن در تکنیک دستهبند بیز ساده، اصول اولیهاش را مرور میکنیم.
اگر فرض کنیم که ویژگیها یا متغیرهای مربوط به مشاهدات، مستقل از یکدیگر هستند، میتوان با فرض وجود متغیر برچسب یا دسته ، قضیه بیز را به صورت زیر نوشت.
در اینجا را «توزیع پسین» (Posterior Probability) و را «توزیع پیشین» (Prior Probability) یا «تابع درستنمایی» (Likelihood Function) میگویند.
فرض کنید دو کلاس و وجود داشته باشد. به این ترتیب قاعده تصمیمگیری بوسیله دستهبند بیز ساده به شکل زیر نوشته خواهد شد.
اگر باشد، را در کلاس قرار میدهیم.
به این ترتیب برای محاسبه هر یک از این احتمالات از قضیه بیز استفاده کرده و مبنا یا تصمیم برای قرارگیری هر مشاهده در گروه یا کلاس به صورت زیر نوشته خواهد شد.
کدی که در ادامه مشاهده میکنید با فرض توزیع نرمال به عنوان توزیع پیشین برای دادهها، الگوریتم دستهبندی بیز ساده را برای دادههای اصلی و استاندارد شده اجرا میکند.
1from sklearn.naive_bayes import GaussianNB
2
3# on non-standardized data
4gnb = GaussianNB()
5fit = gnb.fit(X_train, y_train)
6
7# on standardized data
8gnb_std = GaussianNB()
9fit_std = gnb_std.fit(X_train_std, y_train)گام پنجم: بررسی دقت دستهبندی دادههای اصلی و استاندارد شده
در ابتدا الگوریتم دستهبند بیز ساده را برای دادههای اصلی آموزشی اجرا کرده و صحت و دقت مدل را روی دادههای آموزشی و آزمایشی اندازهگیری میکنیم.
1from sklearn import metrics
2
3pred_train = gnb.predict(X_train)
4
5print('\nPrediction accuracy for the training dataset')
6print('{:.2%}'.format(metrics.accuracy_score(y_train, pred_train)))
7
8pred_test = gnb.predict(X_test)
9
10print('\nPrediction accuracy for the test dataset')
11print('{:.2%}\n'.format(metrics.accuracy_score(y_test, pred_test)))نتیجه اجرای کدهای بالا در ادامه دیده میشوند. همانطور که مشاهده میکنید، دقت تشخیص دسته یا گروهها برای دادههای آموزشی اصلی حدود 81٪ و برای دادههای آزمایشی اصلی تقریبا 65٪ است. که البته مناسب به نظر نمیرسد.
1Prediction accuracy for the training dataset
281.45%
3
4Prediction accuracy for the test dataset
564.81%در قسمت دوم همین عملیات را روی دادههای استاندارد شده آموزشی اجرا کرده و دقت مدل حاصل را براساس دادههای آموزشی و آزمایشی محاسبه میکنیم.
1pred_train_std = gnb_std.predict(X_train_std)
2
3print('\nPrediction accuracy for the training dataset')
4print('{:.2%}'.format(metrics.accuracy_score(y_train, pred_train_std)))
5
6pred_test_std = gnb_std.predict(X_test_std)
7
8print('\nPrediction accuracy for the test dataset')
9print('{:.2%}\n'.format(metrics.accuracy_score(y_test, pred_test_std)))نتیجه اجرای کد بالا، نشانگر افزایش دقت تشخیص گروهها هم برای دادههای آموزشی و هم آزمایش است، بطوری که برای مجموعه داده آموزشی، دقت تشخیص گروه واقعی تقریبا 97٪ و برای دادههای آزمایشی 98٪ است. این نتایج را در کادر زیر مشاهده میکنید.
1Prediction accuracy for the training dataset
296.77%
3
4Prediction accuracy for the test dataset
598.15%بنابراین، مشخص است که استفاده مناسب از دادههای استاندارد شده در تحلیل PCA و پس از آن دستهبند بیز ساده موجب افزایش دقت و صحت دستهبندی دادهها میشود.
اگر مطلب بالا برای شما مفید بوده، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای برنامهنویسی پایتون
- آموزش آمار و احتمال مهندسی
- مجموعه آموزشهای یادگیری ماشین و بازشناسی الگو
- آموزش مقدماتی آمار بیزی
- توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها
- تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده
- یادگیری ماشین به زبان قضیه بیز، بی نظمی شانون و فلسفه
^^













در چه صورتی در مل دسته بندی بیز، بیش برازش و کم برازش اتفاق میافته؟