استاندارد سازی و نرمال سازی داده‌ ها در پایتون – راهنمای کاربردی

یکی از موضوعات پر اهمیت در حوزه «یادگیری ماشین» (Machine Learning) و «داده‌کاوی» (Data Mining) بخصوص در بخش «آماده‌سازی داده‌ها» (Data Preparation)، موضوع «تغییر مقیاس» (Re-scaling) داده‌ها است که معمولا توسط دو روش «استانداردسازی» (Standardization) و «نرمال‌سازی» (Normalization) صورت می‌گیرد. در همین راستا در ادامه این مطلب قصد داریم به همین موضوع یعنی استاندارد سازی و نرمال سازی داده ها در پایتون بپردازیم.

اغلب استانداردسازی را «تبدیلی» (Transformation) در نظر می‌گیرند که با استفاه از آن داده‌ها بدون مقیاس شده و میانگین آن‌ها صفر ($$\mu=0$$) و انحراف معیار نیز برابر با واحد ($$\sigma=۱$$) شود. در عوض نرمال‌سازی (Normalization) به کمک تبدیلی صورت می‌گیرد که باعث شود، تغییرات داده‌ها در فاصله $$[0,1]$$ قرار بگیرد. به این ترتیب «دامنه تغییرات» (Range) داده‌ها برابر با یک واحد (R=1) است.

در این نوشتار، به منظور انجام محاسبات و تبدیل داده‌ها به مقیاس جدید و همچنین انجام تحلیل‌های آماری از زبان برنامه‌نویسی پایتون استفاده خواهیم کرد. همچنین به بررسی و مقایسه این دو نوع تبدیل (استانداردسازی و نرمال‌سازی) می‌پردازیم و آن‌ها را با هم مقایسه می‌کنیم. به این ترتیب قادر خواهیم بود به سوالات زیر پاسخ دهیم.

1. آیا همیشه استفاده از تغییر مقیاس ضروری است؟
2. آیا می‌توان بهترین تبدیل برای استانداردسازی یا نرمال‌سازی را پیدا کرد؟
3. آیا انتخاب نوع تبدیل در نتایج حاصل از الگوریتم‌های دسته‌بندی تاثیر گذار است؟
4. آیا تغییر مقیاس به عنوان یک قسمت مهم در مدل‌سازی محسوب می‌شود؟

اگر برای آشنایی با انواع تبدیل‌ و تغییر مقیاس‌ها احتیاج به پیش‌زمینه دارید، بهتر است مطلب روش‌های استاندارد سازی داده‌ها و تبدیل و پاکسازی داده‌ ها با کتابخانه dplyr و tidyr در R — راهنمای کاربردی را مطالعه کنید. همچنین خواندن نوشتار واریانس و اندازه‌های پراکندگی — به زبان ساده و مقیاس و درک بهتر از آن — به زبان ساده نیز خالی از لطف نیست.

استاندارد سازی و نرمال سازی داده‌ ها

تغییر مقیاس در بیشتر روش و «تکنیک‌های چند متغیره» (Multivariate Techniques) به کار می‌رود. به این ترتیب بزرگی یا کوچکی هر یک از ویژگی‌ها مبنا و ملاک انتخاب یا نقش آن متغیر در مدلسازی نبوده و همه متغیرها دارای اهمیتی برحسب وزن‌ها یا ضرایبی که توسط مدل ایجاد می‌شوند، خواهند بود. معمولا از دو گروه تبدیل برای از بین بردن مقیاس استفاده می‌شود. گروه تبدیلات «استانداردسازی» (Standardize) و گروه تبدیلات «نرمال‌سازی (Normalization). در ابتدا با مفهوم استانداردسازی آشنا شده و سپس به نرمال‌سازی خواهیم پرداخت. همچنین در انتها نیز به کارگیری این دو روش را در نتایج حاصل از میزان رابطه بین متغیرها بوسیله کوواریانس مورد تحلیل قرار می‌دهیم.

استانداردسازی (Standardization)

استاندار‌دسازی یا تبدیل Z-score، برای یک مجموعه داده، بدست آوردن مقدارهایی است که دارای میانگین صفر و واریانس یا انحراف استاندارد ۱ باشند. بنابراین اگر میانگین داده‌های اصلی برابر با $$\mu$$ و انحراف معیار آن‌ها نیز $$\sigma$$‌ باشد، مقدار $$Z$$‌ را براساس رابطه زیر می‌توان بدست آورد.

$$\large Z=\dfrac{x-\mu}{\sigma}$$

به این ترتیب مشخص است که داده‌های تبدیل یافته (Z) دارای میانگین صفر و واریانس ۱ است زیرا براساس این تبدیل خواهیم داشت.

$$\large \overline{Z}= \dfrac{1}{n}\sum_{i=1}^nZ_i=\dfrac{1}{n}\sum_{i=1}^n(\dfrac{x_i-\mu}{\sigma})=\\ \large \dfrac{\overline{x}-\mu}{\sigma}=0$$

رابطه آخر از آنجا برابر با صفر است که «اریبی» (Bias) میانگین نمونه با پارامتر مرکزی جامعه (میانگین جامعه یا $$\mu$$) برابر با صفر است. از طرفی نیز برای محاسبه واریانس نیز داریم:

$$\large \sigma^2_Z= \dfrac{1}{n}\sum_{i=1}^n(Z_i-\overline{Z})^2=\dfrac{1}{n}\sum_{i=1}^n Z_i^2= \sum_{i=1}^n(\dfrac{x_i-\mu}{\sigma})^2=\\ \large \dfrac{1}{\sigma^2}\dfrac{1}{n}\sum(x_i-\mu)^2=\dfrac{\sigma^2}{\sigma^2}=1$$

استانداردسازی زمانی که با ویژگی (Features) و داده‌هایی با مقیاس‌های مختلف سروکار دارید بسیار مهم است. برای مثال در الگوریتم گرادیان کاهشی که یک روش برای بهینه‌سازی محسوب می‌شود، ممکن است بعضی از متغیرها با توجه به مقیاس متفاوتی که دارند، باعث کاهش سریعتر مشتق در یک بُعد شوند. یا به عنوان یک مثال دیگر می‌توان به الگوریتم k-نزدیکترین همسایه (K-Nearest Neighbor- KNN) نیز اشاره کرد که با توجه به مقیاس داده‌ها و بهره‌گیری از تابع «فاصله اقلیدسی» (Euclidean Distance)، وزن بیشتری به متغیرها با مقیاس یا واحدهای بزرگتر بدهد در نتیجه به شکل نادرست گروه یا دسته‌ها تشکیل خواهند شد.

به نظر می‌رسد که تنها روشی که در «یادگیری نظارت شده» (Supervised Learning) بدون در نظر گرفتن مقیاس عمل می‌کند و به شکلی «پایا در مقابل تغییر مقیاس» (Scaled Invariant) است، الگوریتم‌های برمبنای «درخت تصمیم» (Decision Tree) مانند الگوریتم‌CART، هستند زیرا براساس بزرگی و کوچکی مقدارهای در هر بُعد نسبت به یکدیگر عمل کرده و فقط به ترتیب و نه اندازه مشاهدات توجه دارد. در ادامه به معرفی بعضی از الگوریتم‌ها یادگیری ماشین می‌پردازیم که تغییر مقیاس در آن‌ها اهمیت داشته و باعث تغییر در نتایج خواهد شد.

• الگوریتم k-نزدیکترین همسایه (KNN) با تابع فاصله اقلیدسی.
• الگوریتم خوشه‌بندی k-میانگین.
• رگرسیون لجستیک، ماشین بردار پشتیبان (SVM)، شبکه عصبی مصنوعی (ANN) زمانی که از روش بهینه‌سازی گرادیان کاهشی استفاده می‌کنید.
• تحلیل تشخیصی خطی (Linear Discirminant Analysis- LDA)، که به دنبال بهترین تبدیل داده‌ها به منظور بهترین جدا کننده یا تشخیص نقاط، است.

نرمال‌سازی (Normalization)

یکی دیگر از روش‌های تغییر مقیاس، استفاده از روش نرمال‌سازی Min-Max است. به این ترتیب علاوه بر یکسان سازی مقیاس داده‌ها، کران‌های تغییر آن‌ها نیز در بازه $$[0,1]$$ خواهد بود. این تبدیل به صورت زیر تعریف می‌شود.

$$\large X_{norm}=\dfrac{X-X_{min}}{X_{max}-X_{min}}$$

در این رابطه $$X_{min}$$ حداقل مقدارها و $$X_{max}$$ نیز حداکثر مقادیر را نشان می‌دهد.

این شیوه محاسبه اغلب در زمانی استفاده می‌شود که می‌خواهیم میزان شباهت بین نقاط را مشخص کنیم. برای مثال در پردازش تصویر و تشخیص پیکسل‌های مشابه از این تبدیل استفاده شده و سپس از الگوریتم‌های خوشه‌بندی برای کاهش تعداد رنگ استفاده می‌شود.

استانداردسازی و نرمال‌سازی در Scikit-learn

با توجه به قابلیت انجام محاسبات برداری در کتابخانه Numpy در پایتون می‌توان محاسبات و تبدیلات مربوط به استانداردسازی و نرمال‌سازی را انجام داد ولی راه ساده‌تر استفاده از کتابخانه scikit-learn و توابع درون آن است. در ادامه با این توابع آشنا شده و به تحلیل دو مجموعه داده خواهیم پرداخت. در ادامه کدی قابل مشاهد است که مربوط به فراخوانی یک منبع داده و نمایش متغیرها و اطلاعات آن است. این مجموعه داده دارای ۱۳ ویژگی با یک متغیر به عنوان برچسب است که با کدهای ۱ تا ۳ مشخص شده‌اند. از این متغیر برچسب به عنوان شماره گروه استفاده خواهیم کرد.

خروجی این دستورات به صورت زیر خواهد بود.

کاملا مشخص است که میزان بزرگی و مقیاس متغیرها در این مجموعه داده متفاوت هستند. بنابراین احتیاج به استانداردسازی یا نرمال‌سازی است. کدهای زیر به منظور «پیش‌پردازش» (Pre-Processing) داده‌ها و استانداردسازی و تبدیل Min-Max نوشته شده است.

خروجی این برنامه به شکل زیر خواهد بود. مشخص است که میانگین برای هر دو متغیر برابر صفر و واریانس یا انحراف استاندارد نیز برابر با واحد (یک) شده است.

همچنین در بخش بعدی محاسبات مربوط به تغییر مقیاس Min-Max صورت گرفته است. به کد زیر توجه کنید.

خروجی برای این دستورات نیز به شکل زیر خواهد بود. همانطور که می بینید دامنه تغییرات برای هر دو متغیر (در هر بُعد) برابر با ۱ و حداقل مقدار حاصل از تبدیل ۰ و حداکثر ۱ محاسبه شده است.

برای درک تغییراتی که داده‌ها قبل و بعد از این دو تبدیل داشته‌اند، از «نمودارهای پراکندگی» (Scatter Plot) استفاده کرده‌ایم. کد مربوط به ترسیم این نمودارها در ادامه قابل مشاهده است.

همانطور که در نمودار بالا مشاهده می‌کنید، نقاط سبز رنگ تغییر مکان پیدا کرده و حول مقدار صفر در محور افقی پراکنده هستند. با توجه به دامنه تغییراتی که برای داده‌های استاندارد شده وجود دارد (تقریبا اکثر داده‌ها در فاصله ۳- تا ۳ تغییر می‌کنند) پراکندگی در حالت Standardized بیشتر است ولی برای داده‌هایی که توسط تغییر مقیاس Min-Max ساخته شده‌اند و با رنگ آبی مشخض شده‌اند، پراکندگی کوچکتر بوده و دامنه تغییرات آن کوچکتر از داده‌های استاندارد شده است.

حال بهتر است که برحسب سه کلاس و برچسبی که مشاهدات را به سه گروه تقسیم می‌کرد، نمودارهایی برای نمایش پراکندگی داده‌های واقعی، استاندارد شده و Min-Max ترسیم کنیم. کدی که در زیر مشاهده می‌کنید به این منظور نوشته شده است.

نتیجه اجرای این کد در ادامه دیده می‌شود. نمودارها به خوبی نشان می‌دهند که روی محورها تغییر مقیاس رخ داده است و حدود تغییرات داده‌ها کاملا نمایان است.

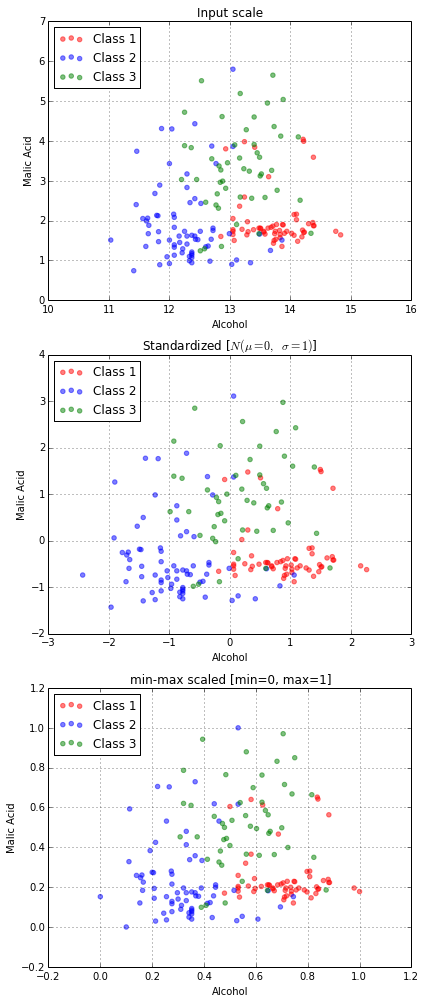
محاسبات مربوط به استانداردسازی و نرمال‌سازی

در ادامه به منظور نمایش تفاوت در نحوه تاثیر این تبدیلات بر داده‌ها و تحلیل‌های آماری و مدل‌سازی به بررسی یک مثال در پایتون خواهیم پرداخت. توجه داشته باشید که داده‌ها هم به صورت استاندارد شده و هم نرمال‌شده درآمده سپس تاثیر آن‌ها بر روی مقدار کوواریانس بین دو متغیر مورد بررسی قرار می‌گیرد.

نکته: توجه داشته باشید که برای محاسبه این تبدیل‌ها به فرمول‌هایی که در بالا به آن‌ها اشاره کردیم، نیاز داریم. واضح است که در این رابطه‌ها $$n$$ تعداد مشاهدات را مشخص می‌کند. البته باید توجه داشت که اگر براساس یک نمونه بخواهیم انحراف معیار را محاسبه کنیم، باید از رابطه زیر کمک بگیریم.

$$\sigma =\left(\dfrac{1}{n-1}\sum_{i=1}^n(x_i-\overline{x})^2\right)^{\frac{1}{2}}$$

در ادامه کدهایی را خواهید دید که با استفاده از دستورات اصلی پایتون (بدون استفاده از کتابخانه) و همچنین بهره‌گیری از توابع موجود در کتابخانه‌ها پایتون محاسبات مربوط به فرمول‌های استانداردسازی و نرمال‌سازی را اجرا می‌کند. البته می‌توانید این کار را با استفاده از دستورات برداری و کتابخانه Numpy در پایتون نیز اجرا کنید.

بدون استفاده از کتابخانه

با استفاده از کتابخانه Numpy

نمایش داده‌ها

برای آنکه نشان دهیم، کدهایی که در قسمت قبل نوشته شده، به درستی کار می‌کنند، نمودار هر یک از داده‌های تبدیل یافته را بوسیله کتابخانه matplotlib و دستورات آن ترسیم می‌کنیم.

میانگین و انحراف معیار برای این داده‌ها به ترتیب برابر با $$\mu=3.8571$$  و $$\sigma=1.8070$$ است. همانطور که در نمودارهای زیر می‌بینید، حدود تغییرات مقدارهای تبدیل شده قابل مشاهده و بررسی است. بنابراین مشخص است که کران‌های داده‌های استاندارد شده در بازه $$[-2.0,1.5]$$ و برای داده‌های نرمال‌شده بازه $$[0,1]$$ است. بنابراین به نظر می‌رسد که تبدیلات به درستی صورت پذیرفته است.

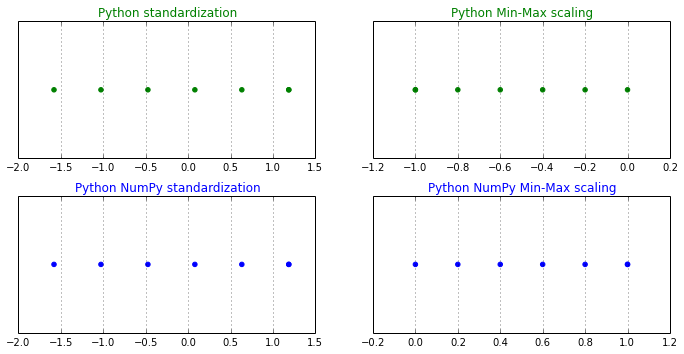
تاثیر تغییر مرکز روی ماتریس کوواریانس

حال که تغییر مقیاس را فرا گرفتیم، باید نشان دهیم که این تبدیلات در میزان وابستگی یا همبستگی بین متغیرها تاثیر گذار نیست در غیر اینصورت، استانداردسازی یا نرمال‌سازی ممکن است، ارتباط بین متغیرها را تحت تاثیر قرار دهد. همانطور که می‌دانید یکی از روش‌های اندازه‌گیری ارتباط بین دو متغیر استفاده از «کوواریانس» (Covariance) است.

فرض کنید $$x$$ و $$y$$‌ دو متغیر هستند و قرار است کوواریانس آن‌ها را محاسبه کنیم. همانطور که در مطلبی از فرادرس با عنوان ضریب‌های همبستگی (Correlation Coefficients) و شیوه‌ محاسبه آن‌ها — به زبان ساده خوانده‌اید، محاسبه کوواریانس به صورت زیر خواهد بود.

$$\large \sigma_{xy}=\dfrac{1}{n-1}\sum(x_i-\overline{x})(y_i-\overline{y})$$

که در آن $$\overline{x}$$ و $$\overline{y}$$ میانگین متغیرهای $$x$$ و $$y$$‌ هستند.

حال با استفاده از تبدیل زیر، اصلاحی انجام می‌دهیم که مرکز (میانگین) متغیرها برابر با صفر شود. این کار را «تبدیل مرکز صفر» (Centering) می‌نامند.

$$\large x^\prime =x-\overline{x}, \;\;\;y^\prime=y-\overline{y}$$

مشخص است که برای داده‌های تبدیل یافته $$x^\prime$$ و $$y^\prime$$، میانگین برابر با صفر است زیرا:

$$\large \overline{x^\prime}=\dfrac{1}{n}\sum_{i=1}^n(x_i-\overline{x})=\overline{x}-\overline{x}=0$$

$$\large \overline{y^\prime}=\dfrac{1}{n}\sum_{i=1}^n(y_i-\overline{y})=\overline{y}-\overline{y}=0$$

با توجه به این تساوی‌ها، مقدار کوواریانس بین دو متغیر $$x$$ و $$y$$ را به شکل زیر محاسبه می‌کنیم.

$$\large \sigma^{\prime}_{xy}=\dfrac{1}{n-1}\sum(x^{\prime}_i-\overline{x^\prime})(y_i^\prime-\overline{y^\prime})$$

همانطور که در قبل نشان داده شد، مرکز یا میانگین هر کدام از متغیرهای تبدیل شده $$x^\prime$$ و $$y^\prime$$، صفر است، فرمول بالا ساده‌تر شده و به شکل زیر در خواهد آمد.

$$\large \sigma^{\prime}_{xy}=\dfrac{1}{n-1}\sum(x^{\prime}_i)(y_i^\prime)$$

که با جایگذاری $$x^\prime=x-\overline{x}$$ و $$y^\prime=x-\overline{x}$$ همان رابطه اولیه برای کوواریانس $$x$$ و $$y$$ حاصل می‌شود. در نتیجه می‌توان گفت که تبدیل مرکز صفر، تاثیری در کوواریانس دو متغیر ندارد.

$$\large \sigma^{\prime}_{xy}=\dfrac{1}{n-1}\sum(x^{\prime}_i-\overline{x^\prime})(y_i^\prime-\overline{y^\prime})=\\ \large \dfrac{1}{n-1}\sum(x^{\prime}_i-0)(y_i^\prime-0)=\\ \large \dfrac{1}{n-1}\sum(x_i-\overline{x})(y_i-\overline{y})=\sigma_{xy}$$

از آنجایی که در شیوه محاسبه تبدیل استاندارد از تغییر مرکز به نقطه صفر استفاده می‌شود، می‌توان گفت که استاندارد‌سازی بوسیله تغییر مکان بر روری کووریانس داده‌ها تاثیر گذار نخواهد بود. همین امر را برای تبدیل Min-Max نیز می‌توان در نظر گرفت. از آنجایی که تغییر مکان داده‌ها باعث تغییر یکسانی در حداکثر و حداقل داده می‌شود، می‌توان گفت که نرمال‌سازی نیز به شکل تغییر مکان، تاثیری در کواواریانس بین دو متغیر نخواهد داشت.

$$\large x^\prime_{norm}=\dfrac{x^\prime -x^\prime_{min}}{x^\prime_{max}-x^\prime_{min}}=\dfrac{x-\mu -(x_{min}-\mu)}{x_{max}-\mu-(x_{min}-\mu)}=\dfrac{x-x_{min}}{x_{max}-x_{min}}=x_{norm}$$

تاثیر تبدیل تغییر مقیاس بر کوواریانس

اگر یک متغیر تغییر مقیاس پیدا کند، مثلا متغیر وزن از کیلوگرم به گرم تبدیل شود، در میزان کوواریانس آن با متغیر دیگر (مثلا قد) تفاوت ایجاد می‌شود. بنابراین تکنیک‌هایی که از ماتریس کوواریانس استفاده می‌کنند (مانند روش تحلیل مولفه‌های اصلی- PCA) تحت تاثیر این تفاوت قرار می‌گیرند.

فرض کنید $$c$$ ضریب تغییر مقیاس برای متغیر $$x$$ باشد. به این ترتیب تبدیل زیر واحد متغیر $$x$$ را تغییر خواهد داد.

$$\large x^{\prime}=c\cdot x$$

در این حالت کوواریانس بین متغیر $$x$$ و $$y$$ قبل و بعد از تغییر مقیاس به صورت زیر خواهد بود.

$$\large \sigma_{xy}=\dfrac{1}{n-1}\sum(x_i-\overline{x})(y_i-\overline{y})$$

$$\large \sigma^{\prime}_{xy}=\dfrac{1}{n-1}\sum(x^{\prime}_i-\overline{x^\prime})(y_i-\overline{y})$$

با توجه به رابطه‌ای که بین $$x$$ و $$x^\prime$$ وجود دارد رابطه بالا به صورت زیر در خواهد آمد.

$$\large \sigma^{\prime}_{xy}=\dfrac{1}{n-1}\sum(cx_i-c\overline{x})(y_i-\overline{y})$$

با فاکتورگیری از مقدار ثابت $$c$$ رابطه بالا به صورت زیر ساده خواهد شد.

$$\large \sigma^{\prime}_{xy}=c\dfrac{1}{n-1}\sum(x_i-\overline{x})(y_i-\overline{y})=c\sigma_{xy}$$

در نتیجه تغییر مقیاس یک یا هر دو متغیر بر روی کوواریانس آن‌ها تاثیر گذار بوده و مقداری که باعث تغییر مقیاس شده در مقدار کوواریانس داده‌های اولیه ضرب می‌شود. به این ترتیب اگر داده‌ها مربوط به وزن را از کیلوگرم به گرم تبدیل کنیم (یعنی ضریب $$c=1000$$)، مقدار کوواریانس بین قد و وزن ۱۰۰۰ برابر خواهد شد.

نکته: به یاد دارید که در تبدیل و تغییر مقیاس استانداردسازی، متغیرها دچار تغییر مرکز صفر و همچنین تغییر مقیاس می‌شوند. به این معنی که اختلاف هر مقدار از میانگین بر انحراف معیار تقسیم می‌شود. بنابراین، استانداردسازی بر روی کوواریانس دو متغیر تاثیر گذار است.

در ادامه نشان خواهیم داد که تغییر مقیاس نرمال‌سازی در کوواریانس بین متغیر $$cx$$ و $$y$$ تغییری بوجود نمی‌آورد.

$$\large x^\prime_{norm}=\dfrac{x^\prime-x^\prime_{min}}{x^\prime_{max}-x^\prime_{min}}$$

مشخص است که رابطه زیر بین حداقل و حداکثر داده‌های تبدیل یافته و اصلی برقرار است.

$$\large x^\prime_{min}=\min(x^\prime)=\min(cx)=c\min(x)$$

$$\large x^\prime_{max}=\max(x^\prime)=\max(cx)=c\max(x)$$

بنابراین نرمال‌سازی شده متغیر تصادفی تغییر مقیاس یافته $$x\prime$$ به شکل زیر خواهد بود.

$$\large x^\prime_{norm}=\dfrac{(x^\prime-x^\prime_{min})}{(x^\prime_{max}-x^\prime_{min})}=\\ \large \dfrac{c(x-x_{min})}{c(x_{max}-x_{min})}=\\ \large \dfrac{(x-x_{min}}{(x_{max}-x_{min})}=x_{norm}$$

به این ترتیب مشخص است که کوواریانس بین متغیرهای تبدیل یافته به روش نرمال‌سازی، تغییری در کوواریانس بین متغیرها بوجود نمی‌آورد.

اگر مطلب بالا برای شما مفید بوده است، احتمالاً آموزش‌هایی که در ادامه آمده‌اند نیز برایتان کاربردی خواهند بود.

• مجموعه آموزش‌های آمار و احتمالات
• آموزش آماده سازی داده ها برای تحلیل آماری در SPSS
• مجموعه آموزش‌های داده کاوی و یادگیری ماشین
• ضریب‌های همبستگی (Correlation Coefficients) و شیوه‌ محاسبه آن‌ها — به زبان ساده
• تحلیل مولفه اساسی (PCA) در پایتون — راهنمای کاربردی
• استخراج (Extraction) و تبدیل (Transformation) داده ها در پایتون — راهنمای جامع

^^