احتمال پسین (Posterior Probability) و احتمال پیشین (Prior Probability) — به زبان ساده

در مباحث مربوط به «آمار بیز» (Bayesian Statistics)، احتمال پسین برای یک متغیر تصادفی همان احتمال شرطی است که براساس شواهد قبلی در مورد رخداد آن پیشامد محاسبه می‌شود. این احتمال شرطی را، احتمال پسین (Posterior Probability) می‌گویند.  از طرف دیگر احتمال کسب چنین شواهدی نیز به احتمال پیشین (Prior Probability) معروف است.

از آنجایی که در ادامه براساس قضیه و رابطه بیز (Bayesian Theorem) پیش خواهیم رفت، مطالعه مطلب قضیه بیز در احتمال شرطی و کاربردهای آن ضروری به نظر می‌رسد. همچنین به منظور اطلاع از خصوصیات تابع احتمال، بهتر است مطلب آزمایش تصادفی، پیشامد و تابع احتمال را قبلا مطالعه کرده باشید. همچنبن خواندن مطلب تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده نیز خالی از لطف نیست.

احتمال پسین

اگر فرض کنیم $$\theta$$ که پارامتر توزیع متغیر تصادفی X است، خود دارای توزیع احتمال باشد و به آن به چشم یک متغیر تصادفی نگاه کنیم، مسئله احتمال پسین پیش می‌آید. به این ترتیب می‌توان این احتمال را به عنوان تابع احتمال متغیر $$\theta$$ به شرط متغیر تصادفی X در نظر گرفت. در این حالت احتمال پسین را به صورت $$P(\theta|X)$$‌ نشان می‌دهند. به این ترتیب قضاوت در مورد پارامتر توزیع می‌تواند با توجه به شواهدی که در مورد آن مشاهده شده (مقدارهای مشاهده شده از متغیر تصادفی X) با دقت بیشتری صورت گیرد.

فیلم آموزش تحلیل های بیزی با نرم افزار وین باگز WinBUGS در فرادرس

کلیک کنید

در مقابل تابع درستنمایی (Likelihood Function)، تابع احتمال متغیر تصادفی X به شرط پارامتر $$\theta$$‌ است، اگر آن را به عنوان تابعی از پارامتر $$\theta$$ نگاه کنیم. در اینجا تابع درستنمایی را به صورت $$P(X|\theta)$$ مشخص می‌کنیم.

رابطه احتمال پسین و پیشین با تابع درستنمایی

این دو بخش توسط رابطه زیر با یکدیگر ارتباط دارند:

فرض کنید که براساس اطلاعات پیشین (Prior Information)، می‌دانیم که تابع احتمال $$\theta$$ به صورت $$\Pi(\theta)$$‌ است و مشاهدات x نیز با تابع درستنمایی $$P(X|\theta)$$ در دسترس هستند. آنگاه تابع احتمال پسین که آن را با $$\Pi(\theta|X=x)$$ نشان می‌دهیم، بر طبق قضیه بیز برابر است با:

$$\large \Pi(\theta |X=x)=\dfrac {P(X|\theta )\Pi(\theta )}{P(X)}$$

توجه کنید که در اینجا تابع «احتمال پیشین» (Prior Probability) برای پارامتر به صورت $$\Pi(\theta)$$ نوشته شده است.

نکته: مخرج کسر به این علت براساس $$P(X)$$ نوشته شده است تا احتمال پسین دارای خصوصیات تابع احتمال باشد، مثلا مقدار آن بین ۰ تا ۱ قرار بگیرد. پس مخرج کسر وظیفه نرمال‌سازی و یا سازگاری محاسبات با مفهوم احتمال را دارد.

اگر بدون در نظر گرفتن مخرج کسر که البته مرتبط با $$\theta$$ نیز نمی‌باشد، رابطه را بررسی کنیم به فرم ساده‌تر زیر می‌توان رسید:

$${\text{Posterior probability}}\propto {\text{Likelihood}}\times {\text{Prior probability}}$$

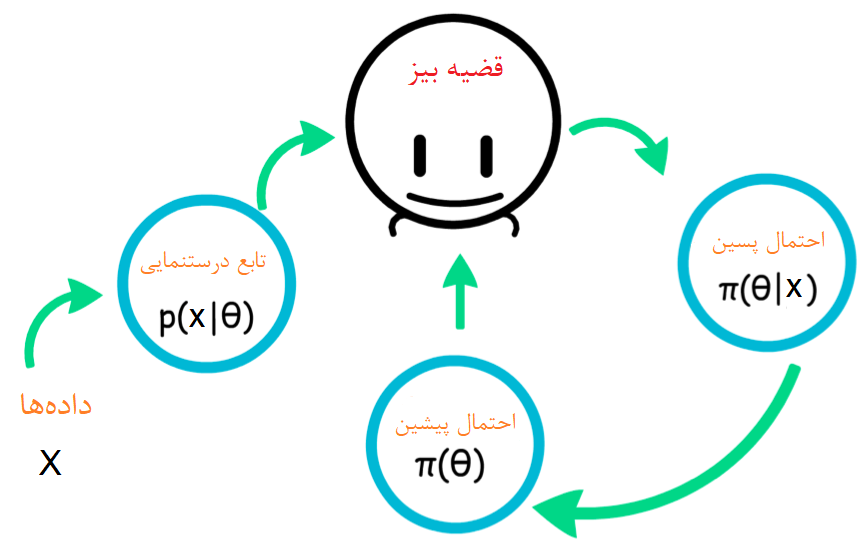
اغلب برای استنباط آماری برای پارامتر توزیع براساس احتمال پسین و پیشین، از رابطه بالا کمک می‌گیرند. همانطور که در تصویر بالا دیده می‌شود، براساس مشاهداتی از X تابع درستنمایی برای پارامتر ساخته می‌شود. با توجه به اصلاعات پیشین که در مورد تابع احتمال پارامتر داریم تفکر و بررسی کرده و به نتیجه جدیدی برای تابع احتمال پارامتر می‌رسیم که به آن تابع احتمال پسین می‌گویند. ممکن است این کار براساس یک نمونه جدید دیگر دوباره انجام شود و در این مرحله تابع پسین قبلی به عنوان تابع پیشین جدید در محاسبات به کار می‌رود.

برای روشن شدن شیوه محاسبه تابع احتمال پسین به کمک قضیه بیز به یک مثال می‌پردازیم.

مثال ۱

فرض کنید در یک مدرسه 60٪ دانش‌آموزان در تورهای فرهنگی و ۴۰٪ نیز در تورهای علمی ثبت نام کرده‌اند. برای تور فرهنگی افراد باید یا دوربین و یا دفترچه یادداشت به همراه داشت باشند. فرض کنید نیمی از دانش‌آموزان تور فرهنگی دارای دوربین و نیمی نیز دفترچه دارند. از طرف دیگر دانش‌آموزان تور علمی باید فقط دفترچه همراه داشته باشند. از بین همه دانش‌آموزان یکی را به تصادف انتخاب می‌کنیم. مشخص می‌شود که او دفترچه به همراه دارد. احتمال اینکه او مربوط به گروه تورهای فرهنگی باشد چقدر است؟

ابتدا تعریف‌های اولیه را مشخص می‌کنیم.

• N پیشامد انتخاب فردی است که دارای دفترچه است.
• D پیشامد انتخاب فردی است که دارای دوربین است.
• C پیشامد انتخاب فردی از گروه تورهای فرهنگی است
• S پیشامد انتخاب فردی از گروه تورهای علمی است.
• $$P(C)$$ احتمال انتخاب دانش‌آموز از گروه تور فرهنگی است (بدون آنکه به تجهیزاتش توجه داشته باشیم). براساس اطلاعات مسئله، مقدار این احتمال برابر با 0.6 است.
• $$P(S)$$ احتمال انتخاب دانش‌آموز از گروه تور علمی است (بدون آنکه به تجهیزاتش توجه داشته باشیم). با توجه به توضیحات گفته شده این احتمال نیز برابر با 0.4 است.
• $$P(N|C)$$ احتمال آن است که فردی که در تور فرهنگی ثبت‌نام کرده، دفترچه همراه داشته باشد. براساس توضیحات مسئله مشخص است که احتمال برابر با 0.5 است.
• $$P(N|S)$$ احتمال داشتن دفترچه در بین افرادی است که در تور علمی ثبت نام کرده‌اند. باز هم می‌دانیم که این احتمال برابر با 1 است.
• $$P(N)$$ احتمال این است که دانش‌آموز انتخابی دفترچه داشته باشد. این احتمال نیز براساس رابطه احتمال کل به صورت زیر قابل محاسبه است:

$$\large P(N)=P(N|C)P(C)+P(N|S)P(S)=$$

$$\large 0.5\times 0.6+1\times 0.4 = 0.7$$

با آگاهی از این اطلاعات، احتمال پسین برای مشاهده فردی با دفترچه از گروه تورهای فرهنگی، به صورت زیر محاسبه می‌شود.

$$\large P(C|N)=\dfrac{P(N|C)P(C)}{P(N)}=\dfrac{0.5\times 0.6}{0.7}=0.43$$

فرم کلی محاسبه احتمال پسین

اگر متغیر تصادفی X با چگالی احتمال $$f_{\theta}(x)$$ (یا درستنمایی $$L_{X}(\theta)$$) و $$\Pi(\theta)$$ نیز تابع احتمال پیشین برای پارامتر $$\theta$$ باشد، آنگاه برای محاسبه تابع احتمال پسین $$\Pi(\theta|X=x)$$ باید محاسبه زیر انجام شود:

 پیوسته: $$\large \Pi(\theta \mid X=x)={\Pi(\theta)L_{X} (\theta) \over {\int _{-\infty }^{\infty }\Pi(\theta)L_u (\theta)\,du}} $$

البته اگر فضای پارامتر $$\theta$$ گسسته باشد باید به جای انتگرال از جمع استفاده کرد:

$$\large \Pi(\theta \mid X=x)={\Pi(\theta)L_{X} (\theta) \over {\sum_{u}\Pi(\theta)L_u(\theta)\,du}} $$: گسسته

نکته: اصطلاح تابع توزیع پسین و پیشین که در مورد پارامتر $$\theta$$ گفته می‌شود، مربوط به رابطه بین پارامتر و مشاهدات متغیر تصادفی X است. اگر در هر روز به یک تابع پسین جدید احتیاج باشد، ممکن است این رابطه را به این صورت در نظر گرفت که توزیع پسین امروز، توزیع پیشین فردا است. این مطلب در تصویر بالا به خوبی دیده می‌شود.

مثال ۲

فرض کنید که متغیر تصادفی X دارای تابع احتمالی طبق جدول زیر باشد. اگر $$\theta$$ دارای توزیع یکنواخت گسسته ($$\Pi(\theta)=\frac{1}{3}$$) باشد، تابع احتمال پسین به صورت زیر محاسبه می‌شود.

باید توجه داشت که جدول بالا در حقیقت چگالی توام متغیرهای تصادفی X و $$\theta$$ را نشان می‌دهد. بنابراین باید تابع احتمال حاشیه‌ای متغیر تصادفی X را نیز محاسبه کنیم. به این ترتیب خواهیم داشت:

$$\large f_X(x)=\sum_{\theta}\Pi(\theta)L_X(\theta)=$$

$$\large \frac{1}{3}\sum_{\theta}L_{X}(\theta)=\begin{cases}\frac{13}{30},\; & x =x_1\\\frac{17}{30},\; & x=x_2\end{cases}$$

در نتیجه با توجه به فرم گسسته تابع پسین خواهیم داشت:

$$\large \Pi({\theta \mid X=x_1})=\begin {cases}{0.2\times \frac{1}{3} \over \frac{13}{30}}=\frac{2}{13},\;& \theta =\theta_1 \\
{0.4\times \frac{1}{3} \over \frac{13}{30}}=\frac{4}{13},\;& \theta =\theta_2\\
{0.7\times \frac{1}{3} \over \frac{7}{30}}=\frac{2}{13},\;& \theta =\theta_3
\end{cases}$$

 و به همین ترتیب برای $$x_2$$:

$$\large \Pi({\theta \mid X=x_2})=\begin {cases}{0.8\times \frac{1}{3} \over \frac{17}{30}}=\frac{8}{17},&\; \theta =\theta_1 \\ {0.6\times \frac{1}{3} \over \frac{17}{30}}=\frac{6}{17},&\; \theta =\theta_2\\ {0.3\times \frac{1}{3} \over \frac{17}{30}}=\frac{3}{17},& \;\theta =\theta_3\end{cases}$$

مثال ۳

فرض کنید $$X\sim B(n,\theta)$$ و $$\theta \in (0,1)$$ و توزیع پیشین برای $$\theta$$ نیز به صورت $$Beta(\alpha,\beta)$$ است که هر دو مقدار $$\alpha,\beta$$ مثبت هستند. روش پیدا کردن احتمال پسین پیوسته طبق رابطه گفته شده، در ادامه خواهد آمد. می‌دانیم که در این مسئله تابع احتمال برای X و $$\theta$$ به صورت زیر است:

$$\large L_{\theta}(x)={ n \choose x}\theta^x (1-\theta)^{(n-x)}, \;\; x=0,1,2,\cdots$$

$$\large \Pi(\theta)={ 1 \over B(\alpha,\beta)} \theta^{(\alpha-1)} (1-\theta)^{(\beta-1)}, \;\; 0 <\theta <1$$

ابتدا تابع احتمال حاشیه‌ای X را پیدا می‌کنیم.

$$\large f_X(x)= \int_0^1{1 \over B(\alpha,\beta)}{ n \choose x}\theta^{(x+\alpha-1)}(1-\theta)^{(n+\beta-x-1)}\;d\theta=$$

$$\large {n \choose x}{B(\alpha+x,n+\beta-x) \over B(\alpha,\beta)}$$

در نتیجه خواهیم داشت:

$$\large \Pi(\theta|x)={L_{X}(\theta)\Pi(\theta) \over f_X(x)}={1 \over B(\alpha+x,n+\beta-x)}\theta^{\alpha+x-1}(1-\theta)^{n+\beta-x-1}$$

نکته: به نظر می‌رسد که توزیع پسین پارامتر $$\theta$$ نیز به صورت $$Beta(\alpha+x,n+\beta-x)$$ در آمده است. می‌توان نتیجه گرفت که اگر توزیع متغیر تصادفی X دو جمله‌ای و توزیع پیشین نیز بتا باشد، آنگاه توزیع پسین باز هم بتا خواهد بود. در نتیجه می‌توان در چنین مواقعی، توزیع پیشین بتا را می‌توان مزدوج توزیع دوجمله‌ای محسوب کرد.

اگر مطلب بالا برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• متغیر های تصادفی – میانگین، واریانس و انحراف معیار – به زبان ساده
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• احتمال شرطی (Conditional Probability) — اصول و شیوه محاسبه
• مجموعه آموزش‌های یادگیری ماشین و بازشناسی الگو
• آموزش آمار و احتمال مهندسی
• آزمایش تصادفی، پیشامد و تابع احتمال
• قضیه بیز در احتمال شرطی و کاربردهای آن
• تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده

^^