متغیر تصادفی و توزیع فوق هندسی (Hyper Geometric) – به زبان ساده

در آزمایش برنولی هر عضو از جامعه آماری یا دارای یک ویژگی (موفقیت) و یا فاقد آن (شکست) است. بر این اساس می‌توان آزمایش تصادفی جدیدی معرفی کرد که نشان دهنده تعداد موفقیت‌ها در یک طرح نمونه‌گیری بدون جایگذاری باشد. از طرفی می‌دانیم، در این حالت اگر نمونه‌گیری با جایگذاری باشد یا اندازه جامعه آماری بزرگ انتخاب شود، یک آزمایش دو جمله‌ای انجام شده است. برای آشنایی بیشتر با مفهوم آزمایش تصادفی و آزمایش برنولی می‌توانید به نوشتار متغیر تصادفی و توزیع برنولی --- به زبان ساده و برای متغیر تصادفی دو جمله‌ای به مطلب متغیر تصادفی و توزیع دو جمله‌ای — به زبان ساده مراجعه کنید.

ولی در این حالت اگر عمل نمونه‌گیری، بدون جایگذاری در نظر گرفته شود، آزمایش تصادفی جدیدی با نام «فوق هندسی» (Hyper Geometric) ایجاد می‌شود.

متغیر تصادفی فوق هندسی

در یک مجموعه N تایی، M عضو دارای ویژگی خاصی هستند. اگر از این مجموعه یک نمونه nتایی بدون جایگذاری تهیه شود یک متغیر تصادفی گسسته به نام متغیر تصادفی فوق هندسی با پارامترهای M، N و n داریم.

اگر این متغیر تصادفی را با X نشان دهیم در این حالت می‌نویسیم $$X\sim HG(N,M,n)$$ و می‌خوانیم X‌ دارای توزیع فوق هندسی با پارامترهای $$M, N$$ و n است.

$$p(X=x)=\dfrac{(^M_x)(^{N-M}_{\;n-x})}{(^N_n)};\;\;\;\;\; \max(0,M+n-N)\leq x\leq \min(n,M); \;\;\; n\leq N$$

با توجه به تعریف گفته شده برای تکیه‌گاه این متغیر تصادفی، مشخص است که حداکثر مقدار x یا n‌ خواهد بود (به این معنی که همه اعضای نمونه دارای ویژگی خاص باشند) و یا مقداری کمتر از M خواهد بود. همچنین حداقل مقدار برای x در حالتی که هیچ عضوی در نمونه، ویژگی خاص ندارد صفر است. واضح است n-x نیز باید بین صفر و N-M باشد پس $$0\leq n- x \leq N-M$$ n در نتیجه $$x \geq n+M-N$$. به این ترتیب حداقل مقدار برای x برابر است با $$\min(0,M+n-N)$$.

اگر تابع احتمال این متغیر تصادفی را برای مقدارهای مختلف n و M و همچنین x رسم کنیم نموداری به شکل زیر ایجاد می‌شود:

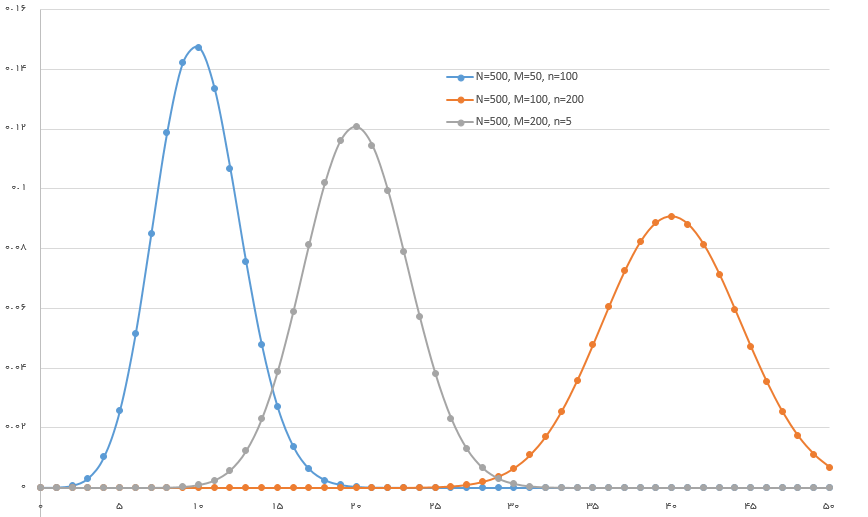
مثال ۱

از بین ۷ کارمند و ۴ سرپرست، یک کمیته سه نفری به تصادف انتخاب می‌شود. احتمال اینکه همه اعضا کارمند باشند چقدر است؟ احتمال اینکه همه اعضای کمیته سرپرست باشند چقدر است؟ احتمال اینکه سرپرست‌ها در اقلیت باشند چقدر است؟

با توجه به تابع احتمال معرفی شده برای توزیع فوق هندسی مشخص است که اگر X  را تعداد کارمندان در کمیته در نظر بگیریم می‌توانیم بنویسیم $$X\sim HG(11,4,3)$$. در نتیجه محاسبات برای قسمت اول سوال به صورت زیر است:

$$P(X=۳)=\dfrac{(^4_0)(^7_3)}{(^{11}_3)}=\dfrac{7}{33}$$

همچنین برای قسمت دوم سوال نیز می‌توانیم به صورت زیر عمل کنیم:

$$P(X=0)=\dfrac{(^4_۴)(^7_0)}{(^{11}_3)}=\dfrac{4}{165}$$

با توجه به مفهوم اقلیت در قسمت سوم سوال کافی است احتمال زیر را محاسبه کنیم:

$$P(X<2)=P(X\leq 1)=P(X=0)+P(X=1)$$

$$=\dfrac{(^4_0)(^7_3)}{(^{11}_3)}+\dfrac{(^4_1)(^7_2)}{(^{11}_3)}$$

$$=\dfrac{35}{165}+\dfrac{84}{165}=\dfrac{119}{165}$$

اگر p درصد افرادی از جامعه با حجم N باشند که دارای ویژگی خاصی هستند، می‌توان متغیر تصادفی فوق هندسی را با پارامترهای N و Np و n معرفی کرد و  نوشت $$X\sim HG(N,Np,n)$$. واضح است که در این حالت M=Np در نظر گرفته شده است.

نکته: اگر N به اندازه کافی بزرگ باشد، می‌توان از توزیع دو جمله‌ای به منظور محاسبه تقریبی احتمال برای متغیر تصادفی فوق‌ هندسی کمک گرفت.

مثال ۲

در هر کارتن بیسکویت،‌ تعداد ۵۰ بسته وجود دارد و احتمال اینکه بسته‌ای در کارتن خرد شده باشد ۱۰٪ است. حال احتمال اینکه در یک نمونه ۵تایی از یک کارتن بیش از ۱ بسته خرد شده باشد چقدر است؟

مشخص است که X، یعنی تعداد بسته‌های خرد شده، دارای توزیع فوق هندسی است. با توجه به اینکه در کارتن ۵۰ تایی تعداد بسته‌های خراب برابر است با $$10٪\times 50=5$$ می‌توانیم بنویسیم $$X\sim HG(50,5,5)$$.

در نتیجه مقدار احتمال اینکه بیش از ۱ بسته در کارتن خراب باشد برابر خواهد بود با:

$$P(X>1)=1-P(X\leq 1)=1-[P(X=0)+P(X=1)]$$

$$=1-[\dfrac{{5 \choose 0}{45 \choose 5}}{{50 \choose 5}}+\dfrac{{5 \choose 1}{45 \choose 4}}{{50 \choose 5}}]=1-0.9282=0.0718$$

حال اگر از تقریب دو جمله‌ای استفاده کنیم می‌توانیم بنوسیم $$X\sim B(5,0.1)$$ پس خواهیم داشت:

$$P(X>1)=1-P(X\leq 1)=1-[P(X=0)+P(X=1)]$$

$$=1-[(0.9)^5+5\times (0.9)^4\times(0.1)]=1-0.9185=0.0815$$

که حدود 0.01 اختلاف دارند.

امید-ریاضی و واریانس برای توزیع فوق هندسی

با توجه به تعریف امید-ریاضی و واریانس می‌توان برای توزیع فوق هندسی این آماره‌ها را محاسبه کرد. اگر $$X\sim HG(N,M,n)$$ باشد، خواهیم داشت:

$$E(X)=n\dfrac{M}{N}$$

$$Var(X)=n\dfrac{M}{N}\times \dfrac{(N-M)}{N}\times \dfrac{N-n}{N-1}$$

کابردهای متغیر تصادفی فوق هندسی

فیلم آموزش برنامه نویسی R و نرم افزار RStudio – مقدماتی در فرادرس

کلیک کنید

در ادامه با دو مثال به بررسی کاربردهای متغیر تصادفی فوق هندسی می‌پردازیم.

مثال ۳

یکی از کاربردهای اصلی برای متغیر تصادفی با توزیع فوق هندسی نمونه گیری بدون جایگذاری است. یک آزمایش تصادفی را در نظر بگیرید که در آن باید n توپ از یک جعبه انتخاب شود. درون این جعبه N توپ وجود دارد که M توپ آن به رنگ سیاه است (واضح است که N-M توپ نیز به رنگ قرمز هستند). فرض کنید که انتخاب توپ سیاه از درون جعبه موفقیت محسوب شود و انتخاب توپ قرمز شکست (درست به مانند آزمایش تصادفی دو جمله‌ای یا برنولی). تعداد موفقیت‌ها یعنی X در این آزمایش تصادفی یک متغیر تصادفی فوق هندسی است که مقدار آن را با x‌ نشان می‌دهیم. به جدول زیر توجه کنید:

حال فرض کنید برای مثال تعداد توپ‌های سیاه برابر با ۵ و تعداد توپ‌های قرمز برابر با ۴۵ باشد. به طور تصادفی از جعبه (بدون نگاه کردن به درون آن) ۱۰ توپ به نوبت انتخاب کرده و روی میز چیده‌ایم (انتخاب بدون جایگذاری). احتمال اینکه دقیقا ۴ توپ از ۱۰ تا سیاه باشند چقدر است؟ این اطلاعات در جدول بالا مشخص شده است. پس می‌توان نوشت $$X\sim HG(50,5,10)$$. حال برای محاسبه احتمال کافی است محاسبات را به صورت زیر انجام دهیم:

$$p(X=x)=P(X=4)=\dfrac{{M \choose x} {N-M \choose n-x}}{N \choose n}= \dfrac{{5 \choose 4}{45 \choose 6}}{50 \choose 10}=\dfrac{5.8145}{10272278170}=0.003965$$

این طور به نظر می‌رسد که انتظار نداریم همه توپ‌های سیاه در انتخاب ما حضور داشته باشند، زیرا تعداد توپ‌های قرمز به نسبت توپ‌های سیاه بیشتر هستند.

مثال ۴

یکی دیگر از کابردهای متغیر تصادفی فوق هندسی، پیدا کردن احتمال رد یک محموله حین بازرسی نمونه‌ای در کنترل کیفیت آماری است. همچنین به کمک احتمال مربوط به متغیر تصادفی فوق هندسی، می‌توان برآوردی برای تعداد ورود کالاهای معیوب به بازار را بدست آورد. بازرسان کیفیت معمولا ۱٪ تا ۱۰٪ محموله‌های کالا را مورد بررسی قرار می‌دهند. شاید بتوان گفت که به طور متوسط این مقدار برابر با ۳٪ است. بنابراین شانس نفوذ یک محموله خراب به بازار زیاد است.
زیرا اگر فرض کنیم ۵٪ محموله‌های انبار مشکل دارند (یعنی 5 تا از ۱۰۰ محموله) ، با بررسی ۳٪ از محموله‌ها شانس اینکه با هیچ محموله معیوبی مواجه نشویم برابر است با ۸۶٪ و احتمال اینکه محموله معیوب شناسایی شود برابر با 14٪=86٪-۱ خواهد بود.
این احتمالات توسط تابع احتمال متغیر تصادفی فوق هندسی محاسبه شده‌اند. در اینجا $$X\sim (100,5,3)$$ تعداد انتخاب محموله‌های معیوب در نظر گرفته شده است.

در چنین وضعیتی حجم نمونه برای رسیدن به حداقل یک محموله معیوب در بازرسی برابر با ۴۵ محموله خواهد بود که نشان می‌دهد باید ۴۵ محموله از ۱۰۰ تا بررسی شود تا احتمال رسیدن به حداقل یک محموله خراب برابر با 96.4٪ باشد. زیرا:

$$P(X=0)={\frac {\binom {100-5}{45}}{\binom {100}{45}}}={\frac {\frac {95!}{50!}}{\frac {100!}{55!}}}=\frac {95\times 94\times \ldots \times 51}{100\times 99\times \ldots \times 56}=\frac{55\times 54\times 53\times 52\times 51}{100\times 99\times 98\times 97\times 96}=4.6٪$$

در نتیجه $$P(X \geq 1)=1-P(X=0)=1-4.6٪=96.4٪$$ که نشان می‌دهد با احتمال زیاد با یک محموله معیوب برخورد خواهیم کرد.
اگر مطلب بالا برای شما مفید بوده است، احتمالاً آموزش‌هایی که در ادامه آمده‌اند نیز برایتان کاربردی خواهند بود.

• مجموعه آموزش های برنامه نویسی متلب برای علوم و مهندسی
• متغیر های تصادفی – میانگین، واریانس و انحراف معیار – به زبان ساده
• آموزش آمار و احتمال مهندسی
• متغیر تصادفی و توزیع برنولی --- به زبان ساده
• متغیر تصادفی و توزیع دو جمله‌ای — به زبان ساده

^^