متغیرهای تصادفی: میانگین، واریانس و انحراف معیار — به زبان ساده

متغیرهای تصادفی، دسته ای از مقادیر ممکن حاصل از فرآیندهای تصادفی هستند. برای مثال انداختن سکه را در نظر بگیرید. ما می‌توانیم شیر یا خط بیاوریم. اگر به هر کدام از این شیر و خط، مقداری اختصاص دهیم، یعنی شیر برابر 0 و خط برابر 1 باشد، در این صورت  یک متغیر تصادفی به نام X داریم:

پس:

• ما یک آزمایش داریم (مانند انداختن سکه)
• به هر اتفاق ممکن، یک مقدار می‌دهیم.
• دسته مقادیر ممکن، یک متغیر تصادفی است.

میانگین، واریانس و انحراف معیار (خطای استاندارد)

هر کدام از شاخص‌های فوق  نماد خاص خود را دارند:

• μ علامت میانگین X است و همچنین بعنوان مقدار یا ارزش مورد انتظار از آن یاد می‌شود.
• (Var(x واریانس X است.
• σ علامت انحراف معیار X است.

فیلم آموزش آمار و احتمال مهندسی – حل تمرین و تست کنکور ارشد در فرادرس

کلیک کنید

میانگین یا مقدار مورد انتظار

هنگامی که ما احتمال P را برای هر مقدار x در نظر می‌گیریم، می‌توانیم مقدار مورد انتظار (میانگین) X را به صورت زیر محاسبه کنیم:

μ = Σxp

نکته: Σ علامت «سیگما» است، و معنی آن جمع کردن است.

برای محاسبه کردن مقدار مورد انتظار:

• هر مقدار را در احتمال آن ضرب کنید.
• سپس مقادیر را با هم جمع کنید.

این یک میانگین وزنی (Weighted Mean) است، یعنی مقادیر با احتمال بیشتر، سهم بیشتری در میانگین خواهند داشت.

فیلم آموزش تئوری احتمالات در فرادرس

کلیک کنید

واریانس

واریانس (Variance) برابر است با:

Var(X) = Σx²p − μ²

برای محاسبه واریانس:

• هر مقدار را به توان دو برسانید و حاصل را در احتمال آن ضرب کنید.
• آنها را با هم جمع کنید. با این کار مقدار Σx²p به دست می‌آید.
• سپس مربع مقدار مورد انتظار (میانگین) μ² را از آن تفریق کنید.

فیلم آموزش آمار و احتمال مهندسی در فرادرس

کلیک کنید

انحراف معیار

انحراف معیار (خطای استاندارد)، برابر با جذر واریانس است:

σ=√Var(X)

یک مثال، کارآمد خواهد بود!

شما تصمیم می‌گیرید که یک فست فود افتتاح کنید، و این آمار را برای فست فود های مشابه یافته‌اید:

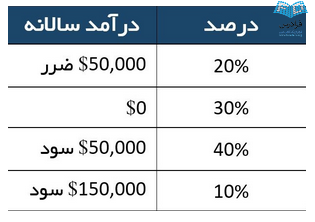
با استفاده از این اطلاعات بعنوان احتمالات، سود فست فود، مقدار مورد انتظار (میانگین) و انحراف معیار چه قدر است؟

متغیر تصادفی همان X (سود ممکن) است.

مقادیر xp و x²p را بدست آورید:

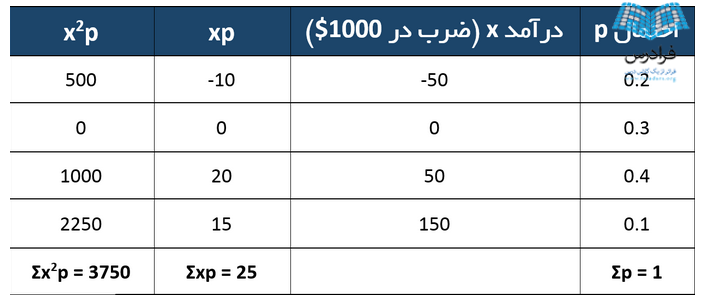
μ = Σxp = 25

Var(X) = Σx²p − μ² = 3750 − 25² = 3750 − 625 = 3125

σ = √3125 = 56 (گرد شده)

به یاد داشته باشید که این مقادیر هر کدام باید ضرب در 1000 دلار شوند، پس:

• μ = $25,000
• σ = $56,000

پس درآمد احتمالی شما برابر با 25,000$ خواهد بود؛ اما انحراف معیار آن بسیار بزرگ است. این مثال را بار دیگر بررسی می‌کنیم، اما این بار از یک احتمال بزرگتر برابر با 50,000$ استفاده می‌کنیم:

مثال (در ادامه مثال قبلی):

اکنون با احتمالات متفاوت (مثلا احتمال 50,000$ بیشتر از قبل و برابر 0.7 است):

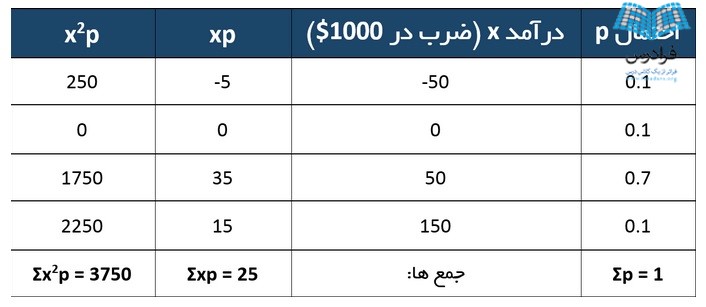
μ = Σxp = 45

Var(X) = Σx²p − μ² = 4250 − 45² = 4250 − 2025 = 2225

σ = √2225 = 47 (گرد شده)

در هزار دلار:

• μ = $45,000
• σ = $47,000

در این حالت میانگین بسیار به عددی که بالاترین احتمال را دارد، نزدیک‌تر است و انحراف معیار مقداری کوچکتر است، چون که مقادیر بیشتر به مرکز نزدیک‌تر هستند.

پیوسته بودن

متغیر های تصادفی می‌توانند پیوسته یا گسسته باشند:

• داده های گسسته فقط می‌توانند به شکل اعداد مشخصی باشند (مثل 1، 2، 3، 4، 5)
• داده های پیوسته می‌تواند هر مقداری را در یک محدوده (برد) خاص شامل شود (مانند قد یک شخص)

در این بخش، ما فقط با داده های گسسته سروکار داشتیم و برای یافتن میانگین، واریانس و انحراف معیار داده های پیوسته، به انتگرال نیاز است.

خلاصه

• یک متغیر تصادفی، متغیری است که مقادیر ممکن آن، نتایج عددی یک آزمایش تصادفی است.
• میانگین (مقدار مورد انتظار) برابر است با: μ = Σxp
• واریانس برابر است با: Var(X) = Σx²p − μ²
• انحراف معیار برابر است با جذر واریانس.

اگر این نوشته مورد توجه شما قرار گرفته است، پیشنهاد می‌کنیم موارد زیر را نیز ملاحظه کنید:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• متغیر تصادفی، تابع احتمال و تابع توزیع احتمال
• مجموعه آموزش‌های دروس رسمی دبیرستان و پیش دانشگاهی
• متغیر تصادفی و توزیع پواسن — به زبان ساده
• متغیر تصادفی و توزیع برنولی — به زبان ساده
• متغیر تصادفی و توزیع هندسی — به زبان ساده
• متغیر تصادفی و توزیع دو جمله‌ای — به زبان ساده
• متغیر تصادفی و توزیع فوق هندسی — به زبان ساده

==