آزمون اندرسون دارلینگ (Anderson-Darling) برای برازش توزیع — پیاده سازی در SPSS
یکی از آزمونهای آماری برازش توزیع، «آزمون اندرسون-دارلینگ» (Anderson-Darling Test) است. این آزمون بررسی میکند که آیا دادهها از توزیع مشخص شده پیروی میکنند یا خیر. با توجه به این موضوع می توان این آزمون را جز گروه روشهای آمار ناپارامتری در نظر گرفت. در فرم اصلی این آزمون، روشی برای برآورد پارامتر توزیع در نظر گرفته نمیشود. در این صورت آماره آزمون و ناحیه بحرانی به صورت ناپارامتری تعیین میشوند. ولی در عمل هنگام استفاده از این آزمون، گروه یا خانوادهای از توزیعها در نظر گرفته میشود و توسط این روش احتیاج است که برآوردی برای پارامترهای توزیع در نظر گرفته شود. این روش بخصوص زمانی که هدف برازش توزیع دادهها با توزیع نرمال است، به خوبی عمل میکند.
در این نوشتار با استفاده از نرمافزار SPSS، براساس یک سری داده شبیهسازی شده، آزمون برازش توزیع «اندرسون-دارلینگ» را اجرا کرده و نتایج را تفسیر میکنیم. به منظور روشنتر شدن موضوع مورد بحث بهتر است مطالب آزمون های فرض و استنباط آماری — مفاهیم و اصطلاحات و توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها را قبلا مطالعه کرده باشید. همچنین خواندن مطلب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال نیز خالی از لطف نیست.
آزمون برازش توزیع اندرسون-دارلینگ (Anderson-Darling Test)
معمولا آزمونهای برازش توزیع، براساس «تابع توزیع تجربی» (Empirical Distribution Function) عمل میکنند. فرض کنید توزیعی که باید مورد بررسی قرار گیرد با $$F$$ و توزیع تجربی دادهها با $$\hat{F}$$ مشخص شده باشد. در آزمون برازش توزیع «اندرسون-دارلینگ» و «آماره کرامر- فن مایسز» (Cramér–von Mises statistics)، مربع فاصله بین این دو توزیع ملاک انجام آزمون است.
این فاصله برای همه دادهها بوسیله رابطه زیر محاسبه میشود.
$$\large n\int _{{-\infty }}^{\infty }(F_{n}(x)-F(x))^{2}\,w(x)\,dF(x)$$
در رابطه بالا منظور از $$w(x)$$ وزن تابعها است. اگر این مقدار برابر با ۱ در نظر گرفته شود $$w(x)=1$$ آماره «کرامر-فن مایسز» حاصل خواهد شد ولی در آزمون «اندرسون-دارلینگ» مقدار $$w(x)$$ مطابق رابطه زیر بدست میآید.
$$\large w(x)=[F(x)\;(1-F(x))]^{-1}$$
مشخص است که روش اندازهگیری فاصله، از رابطه مربع فاصله اقلیدسی گرفته شده است. به این ترتیب آماره آزمون $$A$$ مربوط به آزمون «اندرسون-دارلینگ» توسط رابطه زیر بدست میآید.
$$\large A^{2}=n\int _{-\infty }^{\infty }{\frac {(F_{n}(x)-F(x))^{2}}{F(x)\;(1-F(x))}}\,dF(x)$$
نکته: با توجه به رابطههای بالا، مشخص است که در آزمون «اندرسون-دارلینگ»، وزن بیشتری به مشاهدات موجود در دمها نسبت به آزمون «کرام-فن مایسز» داده میشود.
این روش آزمون و آماره مربوط به آن توسط دو دانشمند آمار به نامهای «تئودور اندرسون» (Theodore Wilbur Anderson) و «دونالد دارلینگ» (Donald Darling) در سال 1952 مطرح شد و امروزه در بسیاری از نرمافزارهای محاسبات آماری به کار گرفته میشود.


مبنای آماره آزمون اندرسون-دارلینگ
در آزمون «اندرسون-دارلینگ» این فرضیه بررسی میشود که آیا دادهها از توزیع مورد نظر گرفته شدهاند یا خیر. در این آزمون، با توجه به صحت این فرضیه، تابع توزیع احتمال تجمعی $$F$$ دارای توزیع احتمال یکنواخت (Uniform Distribution) در فاصله (۱و۰) است، یعنی:
$$\large F \sim Uniform(0,1)$$
مطابق آزمون «شاپیرو» (Shapiro) برای سنجش توزیع یکنواخت برای دادههای $$Y$$ (اگر مشاهدات به صورت $$\{Y_{1}<\cdots <Y_{n}\}$$مرتب شده باشند) آماره آزمون $$A$$ مطابق با رابطه زیر است.
$$\large A^{2}=-n-S\,, S=\sum _{i=1}^{n}{\frac {2i-1}{n}}\left[\ln(F(Y_{i}))+\ln \left(1-F(Y_{n+1-i})\right)\right]$$
با مقایسه مقدار $$A$$ با مقدار بحرانی مطابق توزیع آماره، میتوان به یکنواخت بودن توزیع دادهها رای داد. کاملا مشخص است که در این رابطه احتیاجی به برآورد پارارمترها نیست.
آزمون برازش توزیع دادهها با توزیع نرمال
یکی از بهترین روشها برای سنجش، نرمال بودن دادهها، استفاده از آماره و آزمون «اندرسون-دارلینگ» است. میتوان نشان داد که آماره $$A^2$$ بهترین آمارهای است که میتواند مطابقت توزیع تجربی دادهها را با توزیع نرمال انجام دهد. به منظور بررسی مطابقت توزیع تجربی با توزیع نرمال چهار حالت در نظر گرفته میشود.
- حالت اول: میانگین و واریانس توزیع مشخص است.
- حالت دوم: میانگین نامشخص ولی واریانس مشخص است.
- حالت سوم: میانگین مشخص ولی واریانس نامشخص است.
- حالت چهارم: میانگین و واریانس هر دو نامشخص هستند.
حال فرض کنید که یک نمونه تصادفی nتایی $$X_i,\;i=1,2,\cdots,n$$ به صورت مرتب شده داریم یعنی $$X_1\leq X_2\leq ... \leq X_n$$. در این حالت وضعیت پارامترهای توزیع نرمال و حالتهای انجام آزمون را طبق جدول زیر در نظر میگیریم.
| حالت | حالت اول | حالت دوم | حالت سوم | حالت چهارم |
| برآورد میانگین ($$\hat{\mu}$$) | $$\mu$$ | $$\overline{X}$$ | $$\mu$$ | $$\overline{X}$$ |
| برآوردگر واریانس ($$\hat{\sigma^2}$$) | $$\sigma^2$$ | $$\sigma^2$$ | $$\frac{1}{n}\sum_{i=1}^n(X_i-\mu)^2$$ | $$\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})^2$$ |
حال اگر $$Y_i$$ را براساس $$X_i$$ به صورت زیر استاندارد کنیم، آماره آزمون را به صورت $$A^2$$ محاسبه خواهیم کرد.
$$\large Y_{i}={\frac {X_{i}-{\hat {\mu }}}{{\hat {\sigma }}}}$$
$$\large A^{2}=-n-{\frac {1}{n}}\sum _{{i=1}}^{n}(2i-1)(\ln \Phi (Y_{i})+\ln(1-\Phi (Y_{{n+1-i}})))$$
مشخص است که در رابطه بالا منظور از $$\Phi()$$ تابع توزیع احتمال تجمعی نرمال استاندارد است.
نکته: اگر میانگین و واریانس توزیع هر دو نامشخص باشند میتوان از آماره $$A^{*2}$$ که در ادامه معرفی شده، استفاده کرد.
$$A^{{*2}}={\begin{cases}A^{2}\left(1+{\frac {4}{n}}-{\frac {25}{n^{2}}}\right),&{\text{if the variance and the mean are both unknown.}}\\A^{2},&{\text{otherwise.}}\end{cases}}$$
در سطر اول این آماره، حالتی که هر دو میانگین و واریانس نامشخص هستند، تعیین شده و در غیراینصورت $$A^{*2}=A^2$$ خواهد بود. اگر مقدار آماره آزمون در این روش از مقدار بحرانی بزرگتر باشد، فرض صفر که هماهنگی بودن توزیع دادهها با توزیع نرمال است، رد میشود.
اجرای آزمون برازش توزیع به کمک SPSS
مجموعه دادهای از ۲۵۰ مشاهده را در نظر بگیرید. این اطلاعات در قالب یک فایل فشرده در اینجا قرار گرفته است. پس از دریافت و خارج کردن فایل از حالت فشرده آن را در نرمافزار SPSS باز کنید.
برای انتخاب توزیع مناسب برای این دادهها مراحل زیر را در SPSS پی بگیرید.
۱- از فهرست Analysis گزینه Simulation را انتخاب کنید.
۲- از داخل پنجره Simulation: Model Source گزینه Create Simulated Data را انتخاب سپس دکمه Continue را کلیک کنید.
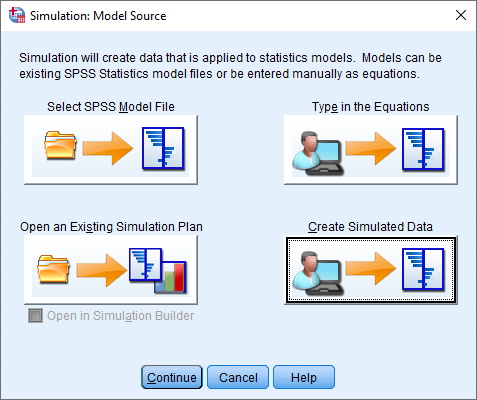
۳- با انتخاب گزینه Create simulated data without a model مشخص کنید که میخواهید برازش توزیع را برای متغیر normrand اجرا کنید. کافی است این متغیر را در کادر Fields to be simulated قرار دهید.
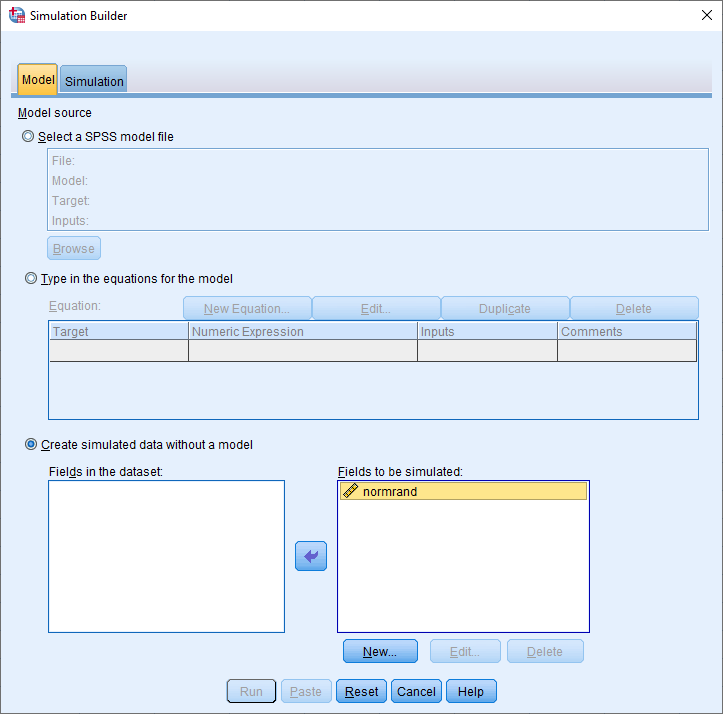
۴- با انتخاب برگه Simulation از قسمت بالایی پنجره، تنظیمات را مطابق تصویر زیر قرار دهید. در قسمت Type در ستون Distribution توزیع دادهها را Normal انتخاب کنید.
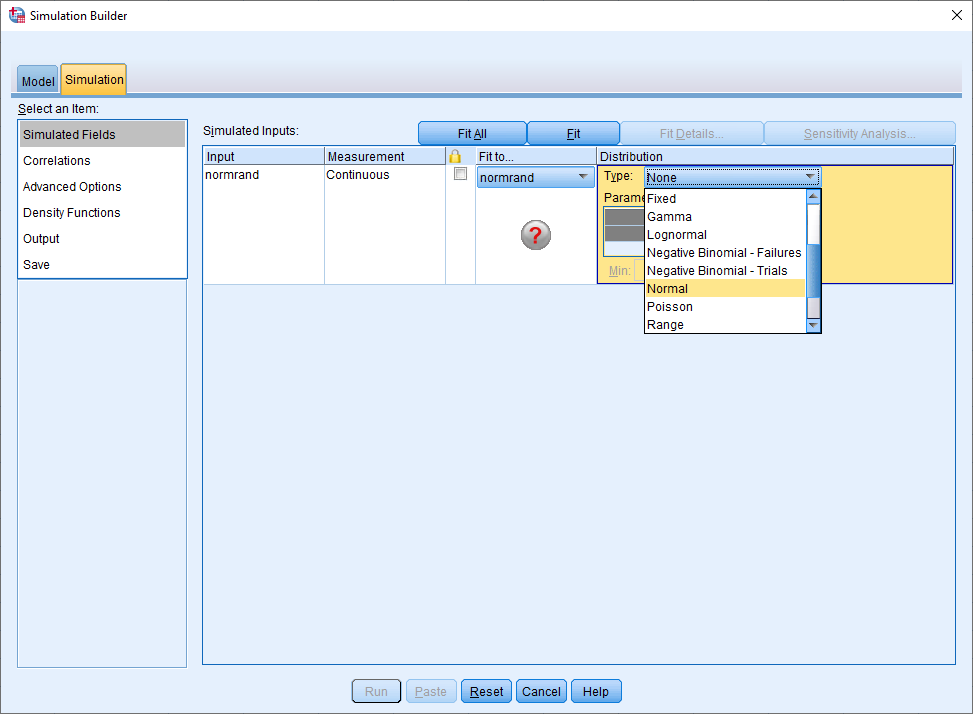
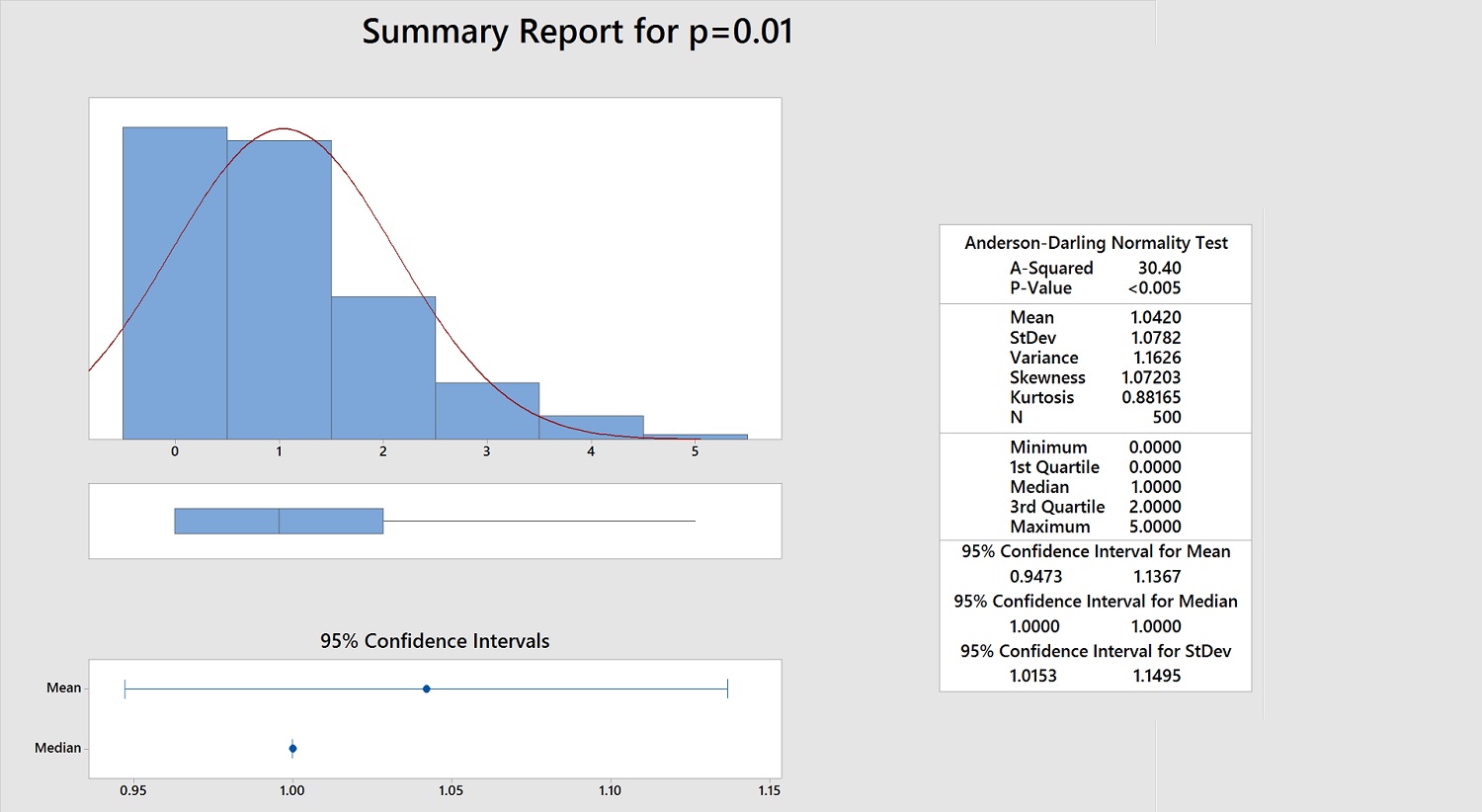
۵- با فشردن دکمه Fit، نمودار برازش (هیستوگرام به همراه منحنی نرمال) ظاهر میشود.
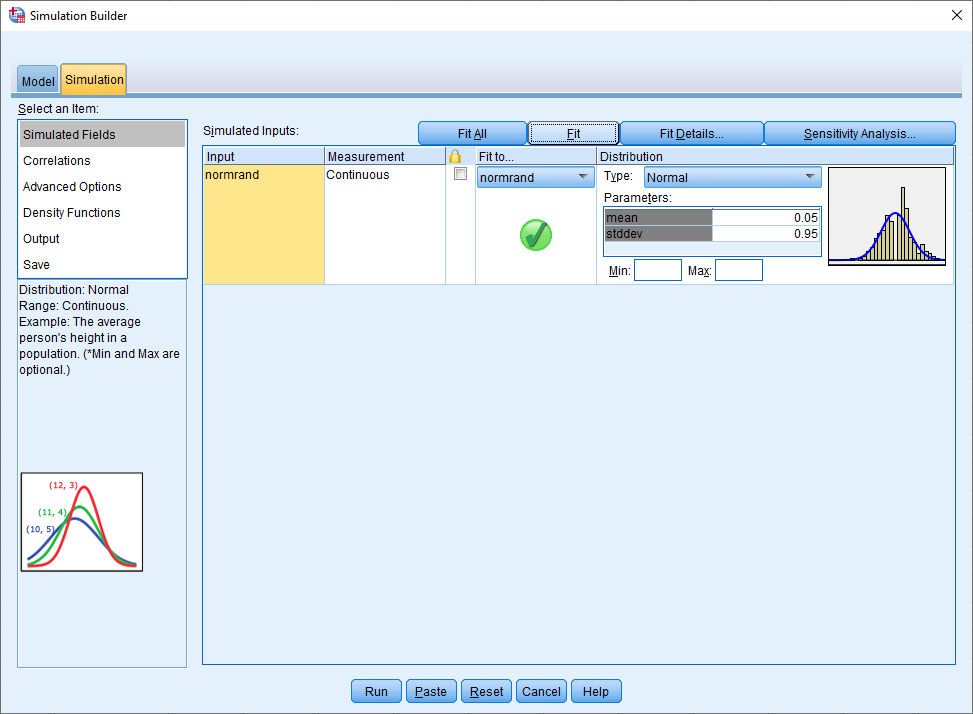
۶- با انتخاب دکمه Fit Detail میتوانید مقدار آماره «اندرسون-دارلینگ» را نسبت به توزیعهای مختلف برای دادهها، مشاهده کنید. لیست ظاهر شده، براساس کوچکترین مقدار آماره مرتب شده است. با توجه به کمترین مقدار آماره برای توزیع نرمال (A=0.67)، همچنین بزرگ بودن مقدار احتمال (0.08=p-value) نسبت به احتمال خطای نوع اول ($$\alpha=0.05$$)، فرض نرمال بودن این دادهها رد نخواهد شد در نتیجه فرض صفر که بیانگر مربوط بودن توزیع دادهها با توزیع نرمال بود، توسط این نمونه تایید میگردد.
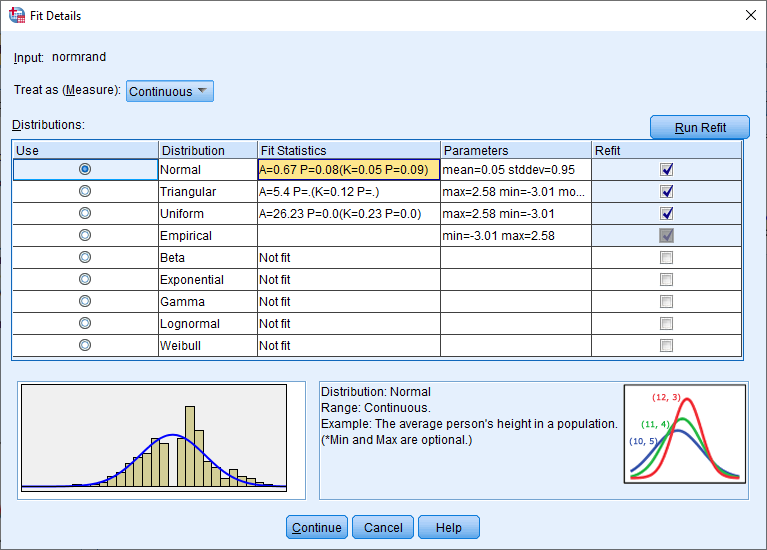
نکته: در قسمت پارامترها (Parameters)، محاسبات مربوط به برآورد میانگین (Mean) و انحراف استاندارد (stddev) براساس جدول بالا و دادههای موجود، صورت گرفته است.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای نرمافزارهای آماری
- آموزش آمار و احتمال مهندسی
- مجموعه آموزشهای آمار احتمالات و دادهکاوی
- آزمایش تصادفی، پیشامد و تابع احتمال
- مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری
- توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها
- توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس
^^








سلام. برای برازش تابع توزیع، تست های کلموگرف-اسمیرنوف و کیس کوئر وجود دارند. سوال این است که تست اندرسون چه تفاوتی با آن دو تست دارد؟ با سپاس
با سلام و احترام
من 12 تا داده دارم که میخوام آنها را به 3 تا بازه تبدیل کنم به طوری که 1- یکی از بازه ها سمت چپ میانگین 12 تا داده باشه(یعنی اعداد داخل بازه کوچکتر از میانگین باشند) و 2- یکی از بازه ها سمت راست میانگین 12 تا داده باشه(یعنی اعداد داخل بازه بزرگتر از میانگین باشند) و نهایتاً 3- سومین بازه طوری تعیین بشه که میانگین 12 تا داده داخل آن بازه قرار بگیره .
به عنوان مثال اگر میانگین 12 تا داده من 5 باشد میخام 3 تا بازه من مثلاً به این صورت باشد (1-3)، (3-7)، (6-10)
امکانش هست راهنمایی کنید که چطور و با چه روشی می تونم 3 تا بازه را تشکیل بدهم که تشکیل بازه ها از نظر علمی منطقی باشه؟
سلام! از اینکه همراه فرادرس هستید سپاسگزاریم!
به کمک طبقهبندی یا دستهبندی Visual Binning در SPSS این کار به راحتی صورت میگیرد.
به مطلب دسته بندی تصویری (Visual Binning) در SPSS — راهنمای کاربردی مراجعه کنید.
در آنجا مشخص شده است که با انتخاب گزینه میانگین و یک انحراف استاندارد میتوانید سه ناحیه را مشخص کرده و مطابق با نظرتان دادهها را طبقهبندی کنید.
باز هم این که همراه فرادرس هستید خوشحالیم،
موفق و سلامت باشید.