توابع گاوسی و کاربرد آنها — به زبان ساده

توابع ریاضی در مدل‌سازی و تشخیص و به کارگیری الگو‌ها، نقش مهم و بسزایی دارند. یکی از معروف‌ترین توابع ریاضی که بخصوص در آمار و مدل‌سازی بسیار محبوب است، توابع گاوسی (Gaussian Functions) است. همچنین حضور توابع گاوسی و کاربرد آن‌ها در مهندسی و علوم داده‌، بسیار چشمگیر است. در این نوشتار به بررسی این گونه توابع می‌پردازیم و خصوصیات آن‌ها را مورد بررسی قرار می‌دهیم.

برای آشنایی بیشتر با مفهوم تابع و توابع نمایی بهتر است ابتدا مطلب مفاهیم تابع – به زبان ساده و مشتق لگاریتم و تابع نمایی — از صفر تا صد را مطالعه کنید.

توابع گاوسی و کاربرد آن‌ها

توابع گاوسی، نوع خاصی از توابع نمایی هستند که در بیان بسیاری از پدیده‌ها کاربرد دارند. معمولا نمای توابع گاوسی به صورت مربع کامل بوده که در مقدار $$-1$$ ضرب شده است. به این ترتیب زمانی تابع گاوسی به حداکثر خود می‌رسد که نمای آن کوچکترین مقدار ممکن باشد. دامنه توابع گاوسی اغلب اعداد حقیقی است. توابع گاوسی را می‌توان به صورت تک متغیره (Univariate) یا چند متغیره (Multivariate) در نظر گرفت. به این معنی که اگر متغیر در این تابع به صورت تک بُعدی باشد، به آن تابع گاوسی تک متغیره گفته می‌شود و اگر این متغیر به صورت چند بُعدی در نظر گرفته شود، تابع گاوسی را چند متغیره می‌نامند.

فیلم آموزش شبیه سازی متغیرهای تصادفی و وابسته در متلب در فرادرس

کلیک کنید

توابع گاوسی، توابعی هستند که برد آن‌ها مجموعه اعداد حقیقی است. به این ترتیب اگر $$f(x)$$‌ متعلق به خانواده توابع گاوسی باشد، در فضای $$p$$ بُعدی خواهیم داشت:

$$\large f(x):\cal{R}^p:\rightarrow \cal{R}$$

ابتدا در مورد توابع گاوسی تک متغیره صحبت کرده، سپس حالت دو و چند متغیره آن را مورد بررسی قرار می‌دهیم.

تابع گاوسی تک متغیره

در ریاضیات، خانواده توابع گاوسی، به توابعی گفته می‌شود که به فرم زیر نوشته می‌شوند.

$$\large {\displaystyle f(x)=ae^{-{\frac {(x-b)^{2}}{2c^{2}}}}},$$

رابطه ۱

که در آن مقادیر $$a$$ و $$b$$ اعداد حقیقی بوده و مقدار حقیقی $$c$$ نیز صفر نیست. این خانواده از توابع به علت تحقیقات زیادی که کارل گاوس (Carl Gauss) در مورد این توابع صورت داد به افتخار او، خانواده توابع گاوسی نامیده می‌شوند. البته گاهی نیز به آن‌ها توابع «زنگی شکل» (Bell Curve) نیز می‌گویند.

نکته: زمانی که مقدار $$a$$ مثبت باشد، برد تابع گاوسی، مجموعه اعداد حقیقی خواهد بود.

در نظریه احتمال و آمار، تابع گاوسی را به صورت یک تابع چگالی احتمال نشان می‌دهند و به صورت زیر پارامترهای آن را مشخص می‌کنند.

$$\large {\displaystyle g(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left((x-\mu )/\sigma \right)^{2}}}$$

رابطه ۲

واضح است که در اینجا مقدار $$b=\mu$$ و $$c=\sigma$$ است که به ترتیب میانگین و انحراف استاندارد توزیع نرمال را نشان می‌دهند. همچنین مقدار $$a=\frac{1}{\sigma\sqrt{2\pi}}$$ خواهد بود،‌ در نتیجه این ضریب مثبت بوده و برد تابع گاوسی را به مجموعه اعداد حقیقی مثبت محدود می‌کند. با استفاده از مشتق نیز می‌توان نشان داد که حداکثر مقدار این تابع در نقطه $$x=\mu$$ حاصل می‌شود. به این ترتیب رابطه زیر برقرار است.

$$\large \max(g(x))=\frac {1}{\sigma {\sqrt {2\pi }}}$$

از کاربردهای مهم توابع گاوسی، می‌توان به شناسایی تابع توزیع نرمال در نظریه توزیع‌های احتمالی (Probability Distribution)، در پردازش سیگنال برای تعریف فیلتر گاوسی (Gaussian Filter) و در پردازش تصویر برای هموارسازی گاوسی (Gaussian blur) اشاره کرد.

خصوصیات خانواده توابع گاوسی

توابع گاوسی، به صورت یک تابع توانی با پایه عدد نپر یا تابع نمایی نوشته می‌شوند که نمای آن تابعی مقعر و به صورت یک چند جمله‌ای درجه ۲ است. به این ترتیب مشخص است که لگاریتم توابع گاوسی به فرم یک چند جمله‌ای درجه ۲ و مقعر در خواهد آمد.

پارامتر $$c$$ در رابطه ۱ با پهنای نمودار در نصف مقدار حداکثر (Full width at half maximum) تابع - که گاهی به آن FWHM‌ نیز می‌گویند - در ارتباط است.

برای بدست آوردن رابطه بین FWHM با پارامتر $$c$$‌ کافی است که مقدار حداکثر تابع را بدست آورده و آن را نصف کنیم. فاصله مقدارهای متناظر چنین نقطه‌ای روی محور افقی مقدار FWHM‌ را نشان می‌دهد که بیانگر میزان گستردگی منحنی یا نمودار تابع گوسی است.

واضح است که مقدار حداکثر تابع (قله نمودار تابع گاوسی) در نقطه $$x=b$$ رخ می‌دهد، زیرا به کمک مشتق داریم:

$$\large [\ln\big(f(x)\big)]'=-\frac{1}{2c^2} (2x-2b)=0\rightarrow (2x-2b)=0 \rightarrow x=b$$

حال لازم است که مقدار حداکثر را محاسبه کنیم. کافی است $$x=b$$ انتخاب شود.

$$\large f(b)=a=\max f(x)$$

حال این مقدار را نصف کرده و مقدار یا مقدارهایی از $$x$$ را پیدا می‌کنیم که رابطه زیر برایشان برقرار باشد.

$$\large \frac{a}{2}=f(x)=ae^{-{\frac {(x-b)^{2}}{2c^{2}}}}$$

باز هم با استفاده از لگاریتم‌گیری معادله حاصل را حل می‌کنیم.

$$\large \ln(\frac{a}{2})=\ln(a)-{\frac{(x-b)^2}{2c^2}}$$

از آنجایی که $$\ln(\frac{a}{2})=\ln(a)-\ln(2)$$ است رابطه بالا به صورت زیر ساده‌تر می‌شود.

$$\large \ln(2)=\frac {(x-b)^{2}}{2c^{2}}$$

با جذر گرفتن از دو طرف معادله خواهیم داشت:

$$\large \sqrt{\ln(2)}=\pm \dfrac{(x-b)}{\sqrt{2}c}\\\large c\sqrt{2\ln(2)}=\pm(x-b)$$

بنابراین اگر $$x_1$$ و $$x_2$$ چنین نقاطی باشند، فاصله بین آن‌ها برابر با FWHM را مشخص می‌کند.

$$\large x_1=b+c\sqrt{\ln(2)}+b, \;x_2=b-c\sqrt{\ln(2)}
\\\large x_1-x_2=b+c\sqrt{2\ln(2)}-(b-c\sqrt{2\ln(2)})=2c\sqrt{2\ln(2)}=\text{FWHM}$$

نکته: گاهی خانواده توابع گاوسی را برحسب FWHM می‌نویسند. به این ترتیب اگر $$w$$ بیانگر این مقدار باشد، توابع گاوسی را به صورت زیر نمایش می‌دهند.

$$\large {\displaystyle f(x)=ae^{-4(\ln 2)(x-b)^{2}/w^{2}}}$$

خانواده توابع گاوسی، تحلیلی بوده و حد آن‌ها زمانی که متغیر به سمت بی‌نهایت برود برابر با صفر است.

$$\large \lim_{x\rightarrow \infty} f(x)=0$$

انتگرال توابع گاوسی همان تابع خطا (Error Function) خواهد بود. به این ترتیب محاسبه انتگرال توابع گاوسی روی ناحیه اعداد حقیقی قابل محاسبه است و داریم:

$$\large \int _{-\infty }^{\infty }e^{-x^{2}}\,dx={\sqrt {\pi }}$$

بنابراین می‌توان در حالت کلی رابطه زیر را برای انتگرال توابع گاوسی نوشت:

$$\large {\displaystyle \int _{-\infty }^{\infty }ae^{-(x-b)^{2}/(2c^{2})}\,dx=ac\cdot {\sqrt {2\pi }}.}$$

بنابراین اگر پارامتر $$a$$ را برابر با $$\frac{1}{c\sqrt{2\pi}}$$‌ در نظر بگیریم حاصل انتگرال بالا برابر با ۱ خواهد شد. چنین تابعی را در حوزه آمار و احتمالات به نام توزیع نرمال یا توزیع احتمال گاوسی با پارامترهای $$\mu=b$$ و $$\sigma^2=c^2$$ می‌شناسند. این تابع در رابطه ۲ مشخص شده است.

نکته: پادمشتق گاوسی، یعنی تابع خطا (Error Function) را نمی‌توان برحسب توابع مقدماتی نوشت. با وجود این، یک جواب دقیق برای انتگرال معین این تابع وجود دارد. برای آشنایی بیشتر با این گونه توابع و نحوه محاسبه انتگرال آن‌ها بهتر است به نوشتار انتگرال گاوسی — از صفر تا صد مراجعه فرمایید.

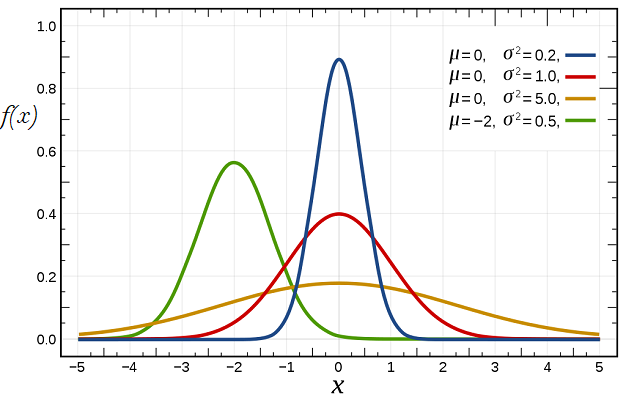
نمودار مربوط به این خانواده از توابع گاوسی با پارامترهای مختلف $$\mu$$ و $$\sigma^2$$ در تصویر زیر دیده می‌شود. وجود حالت زنگی شکل در نمودارها این  تصویر به خوبی دیده می‌شود.

از خصوصیات جالب برای خانواده توابع گاوسی می‌توان به بسته بودن این خانواده از توابع نسبت به ضرب اشاره کرد. اینک به بررسی این موضوع می‌پردازیم. فرض کنید $$f(x)$$ و $$g(x)$$ دو تابع گاوسی به صورت زیر باشند.

$$\large {\displaystyle f(x)=a_fe^{-{\frac {(x-b_f)^{2}}{2c_f^{2}}}}},$$

$$\large {\displaystyle g(x)=a_ge^{-{\frac {(x-b_g)^{2}}{2c_g^{2}}}}}.$$

اگر $$H(x)$$‌ به صورت ضرب این دو تابع در نظر گرفته شود، خواهیم داشت:

$$\large H(x)=f(x).g(x)=a_{_f}e^{-{\frac {(x-b_f)^{2}}{2c_f^{2}}}}a_{_g}e^{-{\frac {(x-b_g)^{2}}{2c_g^{2}}}}=a_{_f}a_{_g}\;e^{-\frac{c_g^2(x-b_f)^2+c_f^2(x-b_g)^2 }{2(c_fc_g)^2}}$$

با ساده کردن نما در این تابع خواهیم داشت.

$$\large H(x)=a_{_f}a_{_g}e^{-\dfrac{(c_g^2+c_f^2)x^2-2(b_1c_g^2+b_gc_1^2)x+(b_f^2c_2^2+b_g^2c_1^2)}{2c_f^2c_g^2}}$$

که با تقسیم صورت و مخرج نما بر $$\_f^2+c_g^2$$ به فرم یک تابع گاوسی مطابق با رابطه ۱ در خواهد آمد.

$$\large H(x)=a_{_f}a_{_g}\exp\Big({-\dfrac{x^2-2\dfrac{(b_fc_g^2+b_gc_f^2)}{(c_g^2+c_f^2)}x+\dfrac{(b_f^2c_g^2+b_g^2c_f^2)}{(c_g^2+c_f^2)}}{2\dfrac{c_f^2c_g^2}{(c_g^2+c_f^2)}}}\Big)$$

که در آن پارامترها به صورت زیر هستند.

$$\large a=a_{_f}a_{_g}\\ \large c=\dfrac{c_f^2c_g^2}{(c_g^2+c_f^2)}\\\large b=\dfrac{(b_fc_g^2+b_gc_f^2)}{(c_g^2+c_f^2)}$$

به این معنی که ضرب دو تابع گاوسی، یک تابع گاوسی خواهد بود. همچنین در مورد ترکیب این دو تابع نیز خواهیم داشت.

نکته: به کمک استقراء می‌توان نشان داد که حاصل‌ضرب n‌ تابع گاوسی نیز یک تابع گاوسی خواهد بود.

خانواده توابع گاوسی دو و چند متغیره

در خانواده تابع گاوسی چند متغیره، نما باید به صورت فرم مربع معین-نامنفی (Negative-definite Quadratic) باشد. در این حالت، باز هم برد یا مجموعه مقادیر خانواده توابع گاوسی، اعداد حقیقی است. ابتدا به معرفی خانواده توابع گاوسی دو متغیره می‌پردازیم.

فیلم آموزش مشتق گیری و انتگرال گیری عددی در محاسبات عددی (رایگان) در فرادرس

کلیک کنید

خانواده توابع گاوسی دو متغیره

اگر دامنه توابع گاوسی را مجموعه نقاط دو بُعدی با مولفه‌های اعداد حقیقی در نظر بگیریم، به فرم تابعی به صورت زیر خواهیم رسید:

$$\large {\displaystyle f(x,y)=A\exp \Big(-\left({\frac {(x-x_{o})^{2}}{2\sigma _{X}^{2}}}+{\frac {(y-y_{o})^{2}}{2\sigma _{Y}^{2}}}\right)\Big).}$$

رابطه ۳

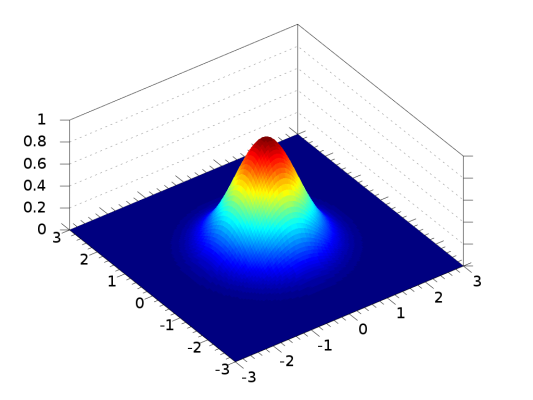
در رابطه ۳، پارامتر $$A$$، ارتفاع نمودار و نقطه $$(x_{o},y_{o})$$‌ مختصات مرکز نمودار را مشخص می‌کند. از طرفی گسترش دم‌های نمودار نیز توسط دو پارامتر $$\sigma_x$$ و $$\sigma_y$$ مشخص می‌شود. در تصویر زیر نموداری از توزیع گاوسی دو متغیره را مشاهده می‌کنید که در آن مرکز برابر است با $$A=1$$، $$(x_{o},y_{o})=(0,0)$$ و $$\sigma_x=\sigma_y=1$$ در نظر گرفته شده است که به نوعی پهنای نمودار را نشان می‌دهد.

سطح مقطع یا کانتورهای این تابع، به شکل بیضی خواهند بود، زیرا نمای تابع به فرم مربع کامل بوده که مکان هندسی نقاط یک بیضی را مشخص می‌کند. در زیر معادله یک بیضی به مرکز $$(x_{o},y_{o})$$ دیده می‌شود که با فرم نما تابع گاوسی مطابقت دارد.

$$\large a(x - x_o)^2 + 2b(x-x_o)(y-y_o) + c(y-y_o)^2$$

رابطه ۴

اگر بخواهیم رابطه ۴ را با فرم تابع گاوسی مطابقت دهیم خواهیم داشت: $$A=1$$، $$a=c=\dfrac{1}{2}$$ و $$b=0$$‌.

نکته: توجه داشته باشید که براساس ضرایب رابطه ۴ باید ماتریس زیر یک ماتریس معین مثبت (Positive Definite) باشد.

$$\large \left[{\begin{matrix}a&b\\b&c\end{matrix}}\right]$$

خانواده توابع گاوسی چند متغیره

فرم کلی و چند متغیره خانواده توابع گاوسی به فرم زیر نوشته می‌شود:

$$\large f(x)=\exp(-x^{T}Ax)\;,$$

که در آن $$x=\{x_{1},\dots ,x_{p}\}$$ یک بردار ستونی $$p$$ سطری است و $$A$$ نیز یک ماتریس معین مثبت $$p\times p$$ است. منظور از $$^T$$ نیز ترانهاده (Transpose)  بردار $$x$$ است. انتگرال این تابع روی فضای $$p$$ بُعدی برابر است با:

$$\large {\displaystyle \int _{\mathbb {R} ^{p}}\exp(-x^{T}Ax)\,dx={\sqrt {\frac {\pi ^{p}}{\det A}}}\;.}$$

اگر دو طرف این رابطه را به عبارت سمت راست تقسیم کنیم، واضح است که انتگرال این نسبت، برابر با ۱ خواهد شد. در نتیجه می‌توان با این کار، فرمی از تابع چگالی نرمال چند متغیره ساخت که در آن $$A$$، معکوس ماتریس واریانس-کوواریانس برای متغیر $$x$$ است.

کاربردهای خانواده توابع گاوسی

در ادامه به لیستی از کاربردها و حوزه‌هایی که خانواده توابع گاوسی در آن‌ها مورد استفاده قرار می‌گیرد، اشاره خواهیم داشت:

• در نظریه احتمال، تابع گاوسی به عنوان یک تابع احتمال به کار گرفته می‌شود که در قضیه حد مرکزی (Central Limit Theorem) نقش اساسی ایفا می‌کند.
• توابع گاوسی به عنوان وضعیت پایه (Ground State) تابع موج برای نوسان‌گر هماهنگ کوانتومی (Quantum Harmonic Oscillator) به کار می‌روند.
• اوربیتال‌های مولکولی (ٰMolecular Orbitals) که در شیمی محاسباتی مورد استفاده قرار می‌گیرند، ترکیب خطی توابع گاوسی موسوم به اوربیتال‌های گاوسی (Gaussian Orbitals) هستند.
• از جنبه ریاضی، مشتق توابع گاوسی را می‌توان به صورت توابع هرمیت (Hermite Function) نشان داد. مشتق مرتبه $$n$$ام توابع گاوسی، باز هم یک تابع گاوسی است که در $$n$$امین چند جمله‌ای هرمیت ضرب شده است.
• توابع گاوسی در شکل‌گیری و تعریف بعضی از شبکه‌های هوش مصنوعی (Artificial Neural Networks) نیز دیده می‌شوند.
• در بحث پردازش سیگنال (Signal Processing)، فیلترهای گاوسی (Gaussian FIlters) توسط توابع گاوسی تعریف و در پردازش تصویر مورد استفاده قرار می‌گیرند.
• در شاخه زمین-آمار (Geostatistics) برای شناخت و تشخیص پراکندگی الگوهای پیچیده از توزیع گاوسی استفاده می‌شود.
• در بحث خوشه‌بندی برمبنای مدل (Model-based Clustering)، توابع گاوسی به عنوان مبدا توزیع احتمالی آمیخته به کار گرفته شده و توسط الگوریتم‌های EM پارامترهای تابع گاوسی برآورد می‌شوند.

خلاصه و جمع‌بندی

خانواده توابع گاوسی را به افتخار دانشمند بزرگ ریاضی، کارل گاوس (Johann Carl Friedrich Gauss) و فعالیت‌های او در زمینه شناسایی خصوصیات این گونه توابع به نام او می‌شناسند. آثار ماندگار او که در زمینه ریاضی و فیزیک در سال‌های پایانی قرن ۱۸ و ابتدای قرن ۱۹ میلادی منتشر شد، او را به تاثیرگذارترین دانشمند در تاریخ ریاضیات تبدیل کرده است. کارل گاوس، علاوه بر ریاضیات و فیزیک، در مهندسی نیز ابداعات زیادی دارد.

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار و احتمالات
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های دروس ریاضیات
• فیلتر کالمن — به زبان ساده
• رسم تابع چگالی احتمال دو بعدی با پایتون — راهنمای کاربردی
• قضیه حد مرکزی و تعمیم آن — به زبان ساده

^^