آزمون دآگوستینو (D’Agostino’s K-squared test) — به زبان ساده
آزمون دآگوستینو (D'Agostino's K-squared test) از آزمونهای ناپارامتری محسوب میشود که به کمک آن قادر هستیم، توزیع دادهها را با توزیع نرمال مقایسه کنیم. در نتیجه میتوان آن را یک آزمون برازش توزیع نرمال محسوب کرد. به کمک این آزمون و آماره آن میتوانید مشخص کنید که آیا دادهها از توزیع نرمال پیروی میکنند یا خیر. از آنجایی که آماره این آزمون، به نام $$K^2$$ مشخص شده و از طرفی توزیع آن نیز به طور مجانبی کای ۲ (Chi Square Distribution) است، گاهی آزمون دآگوستینو (D'Agostino's K-squared test) را به نام آزمون کا دو نیز به کار میبرند.
در این نوشتار با استفاده از نرمافزارهای محاسبات آماری مانند R و پایتون، براساس یک سری داده شبیهسازی شده، آزمون برازش توزیع «دآگوستینو» را اجرا کرده و نتایج را تفسیر میکنیم. به منظور روشنتر شدن موضوع مورد بحث بهتر است مطالب آزمون های فرض و استنباط آماری — مفاهیم و اصطلاحات و توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها را قبلا مطالعه کرده باشید. همچنین خواندن مطلب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال نیز خالی از لطف نیست.
آزمون دآگوستینو (D'Agostino's K-squared test)
در این آزمون فرض صفر به صورتی است که نمایانگر توزیع نرمال برای دادهها است. در فرض مقابل اما عدم نرمال بودن دادهها براساس وجود چولگی (Skewness) و کشیدگی (Kurtosis) در نظر گرفته شده است. بنابراین اگر فرض صفر رد شود، نتیجه خواهیم گرفت که دادهها از یک جامعه با توزیع نرمال گرفته نشدهاند. همچنین اگر فرض صفر رد نشود، میتوان گفت که نمونه تاییدی بر نرمال بودن جامعه آماری ارائه کرده است.
معمولا به منظور تعیین وضعیت رد یا عدم رد فرض صفر به مقدار احتمال (P-value) که در بیشتر نرمافزارهای محاسبات آماری تولید میشود اکتفا میکنیم. چنانچه مقدار .Sig کمتر از 0.05 باشد فرض صفر را رد میکنیم و نتیجه میگیریم که دادههای نمونه از یک جامعه نرمال استخراج نشدهاند.
آزمون دآگوسیتینو، برمبنای تبدیلهایی روی میزان چولگی (Skewness) و کشیدگی (Kurtosis) انجام میشود. بنابراین بهتر است قبل از هر چیز نحوه محاسبه چولگی و کشیدگی را دقیقتر بررسی کنیم.
چولگی و کشیدگی توزیع
فرض کنید $$x_i$$ها نشانگر نمونههایی از یک توزیع احتمالی بوده و $$g_1$$ و $$g_2$$ نیز به ترتیب چولگی و کشیدگی نمونهای هستند. همچنین گشتاور مرکزی $$j$$ام را با $$m_j$$ و میانگین نمونه را با $$\over{x}$$ نشان میدهیم.
مقدار چولگی و کشیدگی براساس گشتاورهای مرکزی مرتبه دوم، سوم و چهارم به صورت زیر محاسبه میشود.
$$\large {\begin{aligned}&g_{1}={\frac {m_{3}}{m_{2}^{{3/2}}}}={\frac {{\frac {1}{n}}\sum _{{i=1}}^{n}\left(x_{i}-{\bar {x}}\right)^{3}}{\left({\frac {1}{n}}\sum _{{i=1}}^{n}\left(x_{i}-{\bar {x}}\right)^{2}\right)^{{3/2}}}}\ ,\\&g_{2}={\frac {m_{4}}{m_{2}^{{2}}}}-3={\frac {{\frac {1}{n}}\sum _{{i=1}}^{n}\left(x_{i}-{\bar {x}}\right)^{4}}{\left({\frac {1}{n}}\sum _{{i=1}}^{n}\left(x_{i}-{\bar {x}}\right)^{2}\right)^{2}}}-3\ .\end{aligned}}$$
رابطه ۱
مقادیر چولگی و کشیدگی که براساس نمونه تصادفی تولید میشوند، میتوانند تقریبی برای برآورد چولگی و کشیدگی توزیع جامعه آماری باشند. البته توجه دارید که اگر نمونهها از یک جامعه آماری با توزیع نرمال گرفته شده باشند، آنگاه میانگین، واریانس، چولگی و کشیدگی این آمارهها نیز قابل محاسبه است. پیرسون در سال ۱۹۳۱ بر این اساس محاسبات زیر را انجام داده است.
او $$\mu_1$$ را برای نمایش میانگین چولگی، $$\mu_2$$ را برای نمایش واریانس و $$\gamma_1$$ را برای نمایش چولگی و $$\gamma_2$$ را برای کشیدگی در نظر گرفت. در نتیجه برای $$g_1$$ و $$g_2$$ که بیانگر آمارههای چولگی و کشیدگی نمونه تصادفی هستند، این مقادیر را فرمولبندی کرد.
آمارههای مربوط به چولگی
$$\large {\begin{aligned}&\mu _{1}(g_{1})=0,\\&\mu _{2}(g_{1})={\frac {6(n-2)}{(n+1)(n+3)}},\\&\gamma _{1}(g_{1})\equiv {\frac {\mu _{3}(g_{1})}{\mu _{2}(g_{1})^{{3/2}}}}=0,\\&\gamma _{2}(g_{1})\equiv {\frac {\mu _{4}(g_{1})}{\mu _{2}(g_{1})^{{2}}}}-3={\frac {36(n-7)(n^{2}+2n-5)}{(n-2)(n+5)(n+7)(n+9)}}.\end{aligned}}$$
رابطه ۲
آمارههای مربوط به کشیدگی
$$\large {\begin{aligned}&\mu _{1}(g_{2})=-{\frac {6}{n+1}},\\&\mu _{2}(g_{2})={\frac {24n(n-2)(n-3)}{(n+1)^{2}(n+3)(n+5)}},\\&\gamma _{1}(g_{2})\equiv {\frac {\mu _{3}(g_{2})}{\mu _{2}(g_{2})^{{3/2}}}}={\frac {6(n^{2}-5n+2)}{(n+7)(n+9)}}{\sqrt {{\frac {6(n+3)(n+5)}{n(n-2)(n-3)}}}},\\&\gamma _{2}(g_{2})\equiv {\frac {\mu _{4}(g_{2})}{\mu _{2}(g_{2})^{{2}}}}-3={\frac {36(15n^{6}-36n^{5}-628n^{4}+982n^{3}+5777n^{2}-6402n+900)}{n(n-3)(n-2)(n+7)(n+9)(n+11)(n+13)}}.\end{aligned}}$$
رابطه ۳
برای مثال اگر یک نمونه ۱۰۰۰ تایی از توزیع نرمال تهیه شود، انتظار داریم (امید ریاضی) چولگی برابر با صفر و واریانس چولگی برابر با تقریبا 0.08 میشود. همچنین چولگی برابر با صفر و کشیدگی نیز مقدار 0.15 خواهد بود.
نکته: نماد $$\mu_2, \mu_3, \mu_4$$ برای نمایش گشتاور مرکزی مرتبه دوم، سوم و چهارم آمارههای چولگی و کشیدگی به کار رفته است.
همانطور که دیده میشود مقدار میانگین (امید ریاضی) و چولگی برای آماره چولگی صفر است. که البته این خاصیت مربوط به توزیعهای متقارن است. از طرفی برای $$n$$های بزرگ (مثلا بزرگتر از ۵۰۰) مقدار چولگی برای آماره کشیدگی تقریبا صفر است.
تبدیلات روی چولگی و کشیدگی نمونهای
توزیع آمارههای چولگی ($$g_1$$) و برجستگی ($$g_2$$) به طور مجانبی نرمال است. نرخ همگرایی به توزیع نرمال بر حسب تعداد نمونه طولانی است و بخصوص برای کشیدگی به ازاء اندازه نمونههای بزرگ حاصل میشود. برای مثال به ازاء $$n=5000$$ میتوان مشاهده کرد که چولگی و کشیدگی آماره $$g_2$$ بزرگتر از 0.1 هستند که قابل چشمپوشی نیست.
به کمک تبدیلی که توسط دآگوستینو ارائه شده است میتوان توزیع این آمارههای نمونهای را به سمت توزیع نرمال استاندارد سوق داد. او تبدیل زیر را برای چولگی ارائه کرد.
$$\large {\displaystyle Z_{1}(g_{1})=\delta \operatorname {asinh} \left({\frac {g_{1}}{\alpha {\sqrt {\mu _{2}}}}}\right),}$$
بطوری که مقادیر ثابت $$\alpha$$ و $$\delta$$ مطابق با رابطههای زیر محاسبه میشوند.
$$\large {\displaystyle {\begin{aligned}&W^{2}={\sqrt {2\gamma _{2}+4}}-1,\\ \large &\delta =1/{\sqrt {\ln W}},\\ \large &\alpha ^{2}=2/(W^{2}-1),\end{aligned}}}$$
واضح است که منظور از $$\mu_2$$ همان واریانس و $$\gamma_2$$ نیز کشیدگی است. پس
$$\large \mu_2 = \mu_2(g_1)\\ \large \gamma_2=\gamma_2(g_1)$$
همچنین تبدیل $$Z_2$$ نیز توسط «انسکومب» (Anscombe) و «گلین» (Glynn) به صورت زیر برای $$g_2$$ معرفی شده است.
$$\large Z_{2}(g_{2})={\sqrt {{\frac {9A}{2}}}}\left\{1-{\frac {2}{9A}}-\left({\frac {1-2/A}{1+{\frac {g_{2}-\mu _{1}}{{\sqrt {\mu _{2}}}}}{\sqrt {2/(A-4)}}}}\right)^{{\!1/3}}\right\},$$
بطوری که مقدار $$A$$ به شکل زیر بدست میآید.
$$\large A=6+{\frac {8}{\gamma _{1}}}\left({\frac {2}{\gamma _{1}}}+{\sqrt {1+4/\gamma _{1}^{2}}}\right),$$
واضح است که منظور از $$\mu_۱$$ و $$\mu_2$$ و همچنین $$\gamma_1$$ مقادیری است که توسط پیرسون بدست آمده است و در رابطه ۲ و ۳ دیده میشود.
آماره آزمون $$K^2$$ در آزمون دآگوستینو (D'Agostino's K-squared test)
اگر دو تبدیل $$Z_1$$ و $$Z_2$$ را با یکدیگر ترکیب کنیم، آماره آزمون دآگوستینو حاصل میشود که به کمک آن میتوانیم دوری از توزیع نرمال را برحسب چولگی و کشیدگی نمونه تصادفی اندازهگیری کنیم.
$$\large K^{2}=Z_{1}(g_{1})^{2}+Z_{2}(g_{2})^{2}\,$$
تحت فرض صفر (نرمال بودن جامعه آماری) توزیع تقریبی $$K^2$$ مطابق با توزیع کای ۲ (Chi Square) با دو درجه آزادی است. جدول زیر تغییرات متوسط آماره و همچنین انحراف استاندارد آن را به ازاء حجم نمونههای مختلف نشان میدهد. همانطور که دیده میشود برای مقدارهای $$n$$ بزرگتر از ۵۰۰، تقریبا توزیع آماره آزمون $$K^2$$ شبیه توزیع کای ۲ است.
| اندازه نمونه | Expected Value | Standard Deviation | 95% Quantile |
|---|---|---|---|
| n = 20 | 1.971 | 2.339 | 6.373 |
| n = 50 | 2.017 | 2.308 | 6.339 |
| n = 100 | 2.026 | 2.267 | 6.271 |
| n = 250 | 2.012 | 2.174 | 6.129 |
| n = 500 | 2.009 | 2.113 | 6.063 |
| n = 1000 | 2.000 | 2.062 | 6.038 |
| χ2(2) distribution | 2.000 | 2.000 | 5.991 |
در ستون Expected Value مقدار متوسط آماره آزمون و در ستون Standard Deviation نیز انحراف استاندارد آن را مشاهده میکنید. همچنین چندک (صدک) ۹۵ام نیز در ستون $$95\%\; \text{Quantile}$$ دیده میشود.
آزمون دآگوستینو در R
در برنامهای که در ادامه مشاهده میکنید، ۱۰۰۰ مشاهده از توزیع کای ۲ با ۱۰ درجه آزادی تولید کردهایم. با توجه نتایجی که آزمون دآگوستینو با تابع agostino.test از کتابخانه moments در زبان برنامه نویسی R دارد، محاسبات صورت گرفته و فرض صفر برای این نمونه رد میشود. از آنجایی که در این آزمون، فرض صفر، نرمال بودن (صفر بودن چولگی و کشیدگی) است، متوجه میشویم که نمونه تصادفی از یک جامعه آماری نرمال گرفته نشده است.
1library(moments)
2n=1000
3set.seed(20)
4x=rchisq(n,df = 10)
5hist(x)
6agostino.test(x)
7par(pty='s')
8qqnorm(x)با اجرای این کد نتایج به صورت زیر خواهد بود.
1 D'Agostino skewness test
2
3data: x
4skew = 0.89448, z = 10.08385, p-value < 2.2e-16
5alternative hypothesis: data have a skewnessاز آنجایی که مقدار احتمال p-value کوچکتر از 0.001 است، فرض صفر یعنی نرمال بودن را رد میکنیم. در ادامه نیز نمودارهای فراوانی و چندک-چندک نیز به منظور تایید نتایج بدست آمده ترسیم شده است.
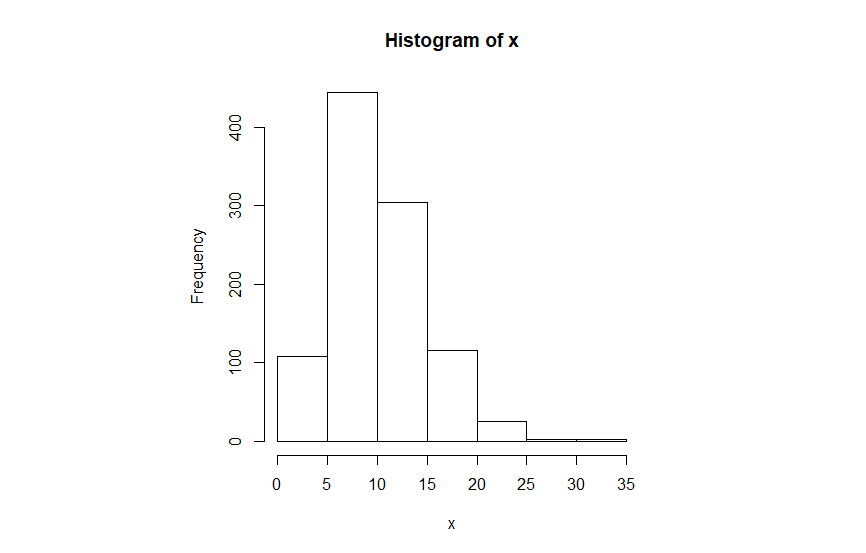
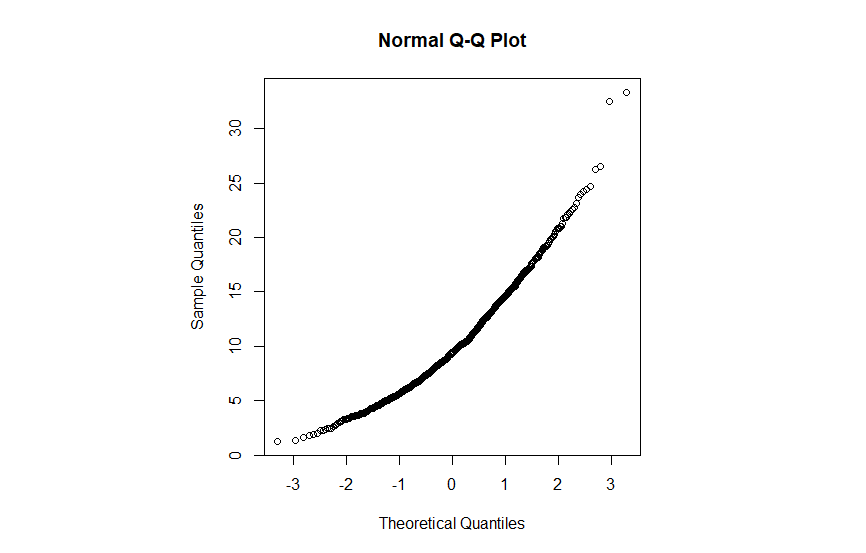
آزمون دآگوستینو در پایتون
کد زیر به منظور انجام محاسبات مربوط به آزمون دآگوستینو نوشته شده است. برای انجام این آزمون، لازم است از کتابخانه SciPy و توابع stats استفاده کرده و آزمون را به کمک normaltest انجام دهیم.
همانطور که مشخص است، ابتدا هزار داده تصادفی از توزیع نرمال استاندارد تولید شده و سپس از توزیع نرمال با میانگین ۲ و انحراف استاندارد ۱ نیز هزار داده دیگر ایجاد میشود. این دو دسته داده در کنار یکدیگر مجموعه x را تشکیل میدهند که مبنای انجام آزمون دآگوستینو است.
1from scipy import stats
2pts = 1000
3np.random.seed(28041990)
4a = np.random.normal(0, 1, size=pts)
5b = np.random.normal(2, 1, size=pts)
6x = np.concatenate((a, b))
7k2, p = stats.normaltest(x)
8alpha = 1e-3
9print("p = {:g}".format(p))
10
11if p < alpha: # null hypothesis: x comes from a normal distribution
12 print("The null hypothesis can be rejected")
13else:
14 print("The null hypothesis cannot be rejected")براساس مقدار احتمال (P-value) محاسبه شده، برنامه تصمیم میگیرد که فرض صفر رد شده یا خیر. در صورتی که مقدار احتمال از 0.001 کوچکتر باشد، فرض صفر رد شده و مشخص میشود که نمونه حاصل از جامعه آماری بیانگر غیرنرمال بودن توزیع جامعه آماری است. در غیر اینصورت دلیلی بر نرمال فرض نکردن جامعه آماری وجود ندارد.
نتیجه اجرای برنامه در ادامه دیده میشود.
1p = 3.27207e-11
2
3
4The null hypothesis can be rejecteبا توجه به اینکه مقدار احتمال بسیار به صفر نزدیک است، فرض صفر رد شده و تشخیص میدهیم که مجموعه دادههای x از یک جامعه با توزیع نرمال استخراج نشدهاند.
خلاصه و جمعبندی
در این نوشتار به بررسی آماره و آزمون دآگوستینو (D'Agostino's K-squared test) پرداختیم و با نحوه محاسبه آن در چند نرمافزار محاسبات آماری نظیر R و پایتون آشنا شدیم. مشخص است که این توزیع برمبنای مطابقت چولگی و کشیدگی دادهها با توزیع نرمال عمل کرده و میتوان از آن به عنوان ابزار سنجش برازش توزیع نرمال استفاده کرد. ولی به هر حال استفاده از روشهای تصویری نظیر نمودار چندک-چندک یا Q-Q plot نیز در تصمیم نهایی میتواند نقش مهمی داشته باشد.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای نرمافزارهای آماری
- آموزش آمار و احتمال مهندسی
- مجموعه آموزشهای آمار احتمالات و دادهکاوی
- مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری
- توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها
- توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس
^^