آزمون شاپیرو ویلک (Shapiro-Wilk Test) — به زبان ساده

«آزمون شاپیرو ویلک» (Shapiro-Wilk Test) از آزمون‌های برازش توزیع نرمال محسوب می‌شود. به کمک این آزمون و آماره آن می‌توانید مشخص کنید که آیا داده‌ها از توزیع نرمال پیروی می‌کنند یا خیر. با توجه به این موضوع می توان این آزمون را جز گروه روش‌های آمار ناپارامتری در نظر گرفت. در فرم اصلی این آزمون، روشی برای برآورد پارامتر توزیع در نظر گرفته نمی‌شود. در شیوه محاسبه آماره در آزمون شاپیرو ویلک (Shapiro-Wilk Test) از آماره‌های ترتیبی و توزیعشان و همچنین و داده‌های اصلی استفاده می‌شود و از این جهت آن را به عنوان روشی ناپارامتری در نظر می‌گیرند.

در این نوشتار با استفاده از نرم‌افزارهای محاسبات آماری مانند SPSS ،R و پایتون، براساس یک سری داده شبیه‌سازی شده، آزمون برازش توزیع «شاپیرو-ویلک» را اجرا کرده و نتایج را تفسیر می‌کنیم. به منظور روشن‌تر شدن موضوع مورد بحث بهتر است مطالب آزمون های فرض و استنباط آماری — مفاهیم و اصطلاحات و توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها را قبلا مطالعه کرده باشید. همچنین خواندن مطلب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال نیز خالی از لطف نیست.

آزمون شاپیرو ویلک

همانطور که در در دیگر نوشتارهای فرادرس با موضوع استنباط آماری بیان شده، هر آزمون فرضیه آماری دارای دو فرض است که با «فرض صفر» (Null Hypothesis) و «فرض مقابل» (Alternative Hypothesis) شناخته می‌شوند. در آزمون شاپیرو ویلک (Shapiro-Wilk Test)، فرض صفر به صورتی است که نمایانگر توزیع نرمال برای داده‌ها است.

فیلم آموزش شبیه سازی متغیرهای تصادفی و وابسته در متلب در فرادرس

کلیک کنید

این روش آزمون بر اساس تحقیقات دو دانشمند «ساموئل شاپیرو» (Samuel Sanford Shapiro) آمارشناس آمریکایی و «مارتین ویلک» (Martin Wilk) آمارشناس کانادایی توسعه و به کار گرفته شد.

در فرض مقابل اما عدم نرمال بودن داده‌ها در نظر گرفته شده است. بنابراین اگر فرض صفر رد شود، نتیجه خواهیم گرفت که داده‌ها از یک جامعه با توزیع نرمال گرفته نشده‌اند. همچنین اگر فرض صفر رد نشود، می‌توان گفت که نمونه تاییدی بر نرمال بودن جامعه آماری ارائه کرده است.

معمولا به منظور تعیین وضعیت رد یا عدم رد فرض صفر به مقدار احتمال (P-value) که در بیشتر نرم‌افزارهای محاسبات آماری تولید می‌شود اکتفا می‌کنیم. چنانچه مقدار .Sig کمتر از 0.05 باشد فرض صفر را رد می‌کنیم و نتیجه می‌گیریم که داده‌های نمونه از یک جامعه نرمال استخراج نشده‌اند.

آماره شاپیرو ویلک

فرض کنید $$x_1, x_2,\ldots,x_n$$ مشاهدات از متغیر تصادفی $$X$$ باشند. اگر $$x_{(i)}$$ آماره‌های ترتیبی برای این متغیر تصادفی باشند، آنگاه آماره آزمون شاپیرو ویلک (Shapiro-Wilk Test) به صورت زیر تعریف می‌شود.

$$\large {\displaystyle W={\left(\sum _{i=1}^{n}a_{i}x_{(i)}\right)^{2} \over \sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}},}$$

در نظر داشته باشید که منظور از $$a_i$$، برداری است که به صورت زیر تعریف شده است.

$$\large {\displaystyle (a_{1},\dots ,a_{n})={m^{\mathsf {T}}V^{-1} \over C},}$$

در رابطه اخیر، $$V$$ ماتریس کوواریانس آماره‌های ترتیبی است. همچنین بردار $$C$$ نیز به صورت زیر بدست می‌آید.

$$\large {\displaystyle C=\|V^{-1}m\|=(m^{\mathsf {T}}V^{-1}V^{-1}m)^{1/2}}$$

و بردار $$m$$ نیز مقدار امید ریاضی آماره‌های ترتیبی است. مشخص است که منظور از $$\bar{x}$$ میانگین مقادیر مشاهده شده از نمونه تصادفی است. یعنی داریم:

$$\large \overline {x}=\left(x_{1}+\cdots +x_{n}\right)/n$$

نکته: به تفاوت بین $$x_i$$ و $$x_{(i)}$$ توجه داشته باشید. اولی مقدار نمونه تصادفی و دومی آماره ترتیبی (مقادیر مرتب شده) متغیر تصادفی $$X$$ هستند.

شبیه‌سازی براساس تکنیک مونت کارلو (Monte Carlo Simulation) نشان داده است که آزمون شاپیرو ویلک (Shapiro-Wilk Test) نسبت به آزمون‌ها دیگر مانند آزمون کولموگروف اسمیرنف (Kolmogorov-Smirnov) و آزمون اندرسون دارلینگ (Anderson-Darling) از توان بیشتری برخوردار است.

انجام محاسبات آزمون شاپیرو ویلک در R

در این قسمت به بررسی نحوه اجرای آزمون شاپیرو ویلک در نرم‌افزار محاسبات آماری R‌ خواهیم پرداخت. فرض کنید یک نمونه تصادفی از توزیع نرمال با پارامترهای میانگین ۵ و واریانس ۱۰۰ داریم. این داده‌ها در متغیر x ثبت شده‌اند. می‌خواهیم به کمک تابع shapiro.test آزمون نرمال بودن چنین داده‌هایی را مشخص کنیم.

کدهای زیر به این منظور نوشته شده‌اند.

1set.seed(123)
2n=1000
3x=rnorm(n,5,sqrt(100))
4shapiro.test(x)
5qqnorm(x)

نتیجه اجرای این کد، محاسبه آماره و مقدار احتمال (p-value) برای آزمون شاپیرو ویلک است. در انتها نیز نمودار چندک-چندک برای مطابقت تصویری آزمون با توزیع نرمال ترسیم شده است.

1Shapiro-Wilk normality test
2
3data:  x
4W = 0.99838, p-value = 0.4765

از آنجایی که مقدار احتمال (p-value=0.4765) کوچکتر از خطای در نظر گرفته شده یعنی 0.05 است، فرض صفر که نرمال بودن داده‌ها است رد نمی‌شود. به این ترتیب نمونه تصادفی دلیلی بر نداشتن توزیع نرمال برای داده‌ها ارائه نکرده است.

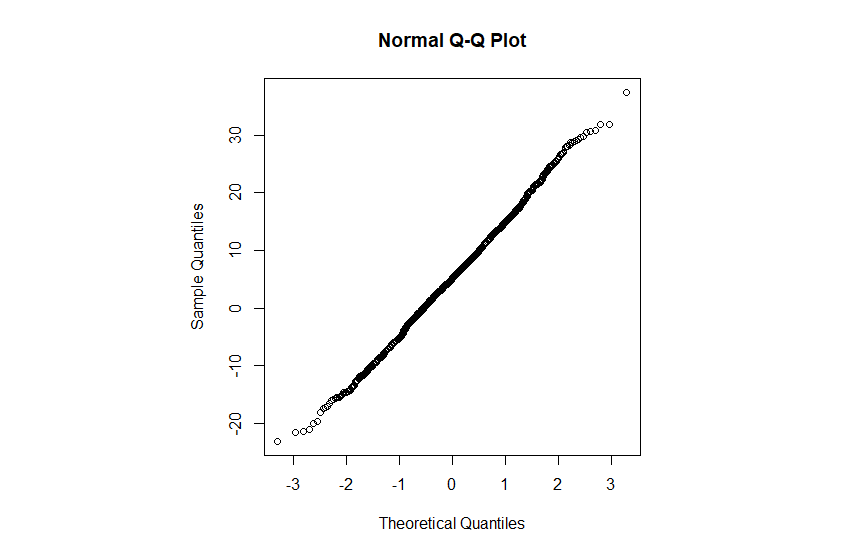
از طرفی نمودار Q-Q plot‌ نیز فرضیه نرمال بودن جامعه آماری را تایید می‌کند.

انجام محاسبات آزمون شاپیرو ویلک در پایتون

این‌ بار از کدهای زیر و تابع shapiro از کتابخانه SciPy.stats برای انجام محاسبات آزمون شاپیرو ویلک در پایتون استفاده می‌کنیم. در اینجا هزار داده از توزیع نرمال با میانگین ۵ و انحراف استاندارد ۳ تولید کرده‌ایم و آماره آزمون و مقدار احتمال را محاسبه و چاپ کرده‌ایم.

1import numpy as np
2from scipy import stats
3np.random.seed(12345678)
4x = stats.norm.rvs(loc=5, scale=3, size=1000)
5stest=stats.shapiro(x)
6print(stest)

نتیجه اجرای این برنامه به صورت زیر خواهد بود.

1(0.9987979531288147, 0.753572940826416)

با توجه به مقدار احتمال 0.75 که بزرگتر از 0.05 یعنی احتمال خطای نوع اول است، فرض صفر رد نشده و رای به نرمال بودن داده‌ها می‌دهیم.

انجام محاسبات آزمون شاپیرو ویلک در SPSS

داده هایی مطابق با تصویر زیر در کاربرگ SPSS وارد شده‌اند و می‌خواهیم براساس آزمون شاپیرو ویلک نرمال بودن آن‌ها را بسنجیم. برای انجام این کار کافی است از دستور Explore از فهرست Analysis‌ استفاده کرده و تنظمیات را مطابق با تصویر انجام دهیم.

فیلم مجموعه آموزش آمار و احتمالات – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

همانطور که دیده می‌شود متغیر مورد نظر را در کادر Dependent List قرار داده‌ایم و در کادر Display فقط گزینه Plot را انتخاب کرده‌ایم. همچنین با کلیک روی دکمه Plots گزینه‌های مرتبط با انجام آزمون شاپیرو-ویلک را برگزیده‌ایم.

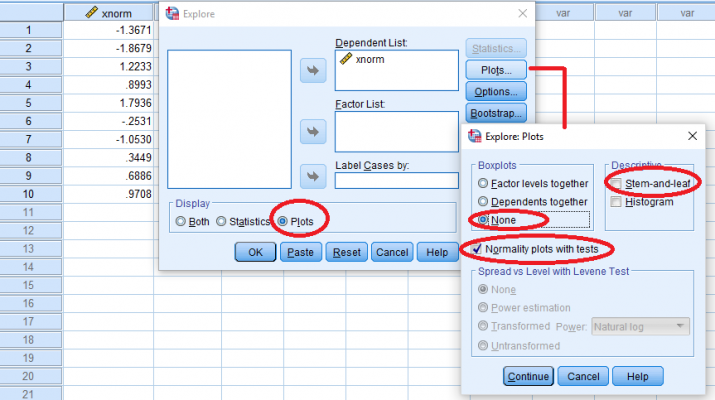
با فشردن دکمه Continue در پنجره Explore Plots و بازگشت به پنجره Explore تنظمیات کامل شده و با کلیک روی دکمه OK محاسبات انجام شده و خروجی نمایش داده خواهد شد. در تصویر زیر این خروجی دیده می‌شود.

نکته: اگر می‌خواهید این دستورات را به کمک محیط Syntax اجرا کنید، باید کدهای زیر را در پنجره مربوطه وارد کرده و دکمه اجرا (Run) را فشار دهید.

1EXAMINE VARIABLES=xnorm 
2  /PLOT NPPLOT 
3  /STATISTICS NONE 
4  /CINTERVAL 95 
5  /MISSING LISTWISE 
6  /NOTOTAL.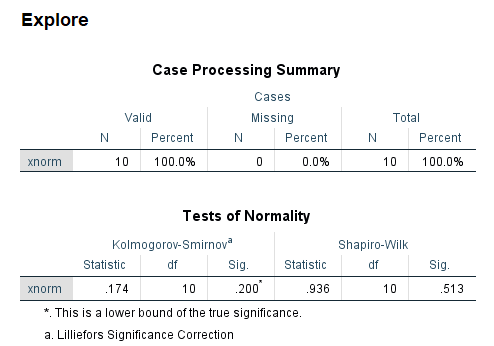

جدول اول با نام Case Processing Summary، اطلاعاتی در مورد تعداد مشاهدات و درصد داده‌های گمشده ارائه شده است. در جدول دوم یا Tests pf Normality، آماره‌ها و مقدار احتمال برای آزمون‌های نرمال بودن دیده می‌شود. با توجه به مقدار Sig که در ستون آخر جدول دوم دیده می‌شود، توزیع داده‌ها نرمال در نظر گرفته می‌شود. این نتیجه با آزمون کولموگروف-اسمیرنوف (Kolmogrove-Smirnov) که مقدار Sig برایش برابر با 0.200 است، نیز مطابقت دارد. در انتها نیز نمودار Q-Q plot برای نمایش تصویری برازش توزیع داده‌ها با توزیع نرمال ترسیم شده است. همچنین نمودار فاصله مشاهدات از توزیع نرمال متناظر در انتها دیده می‌شود.

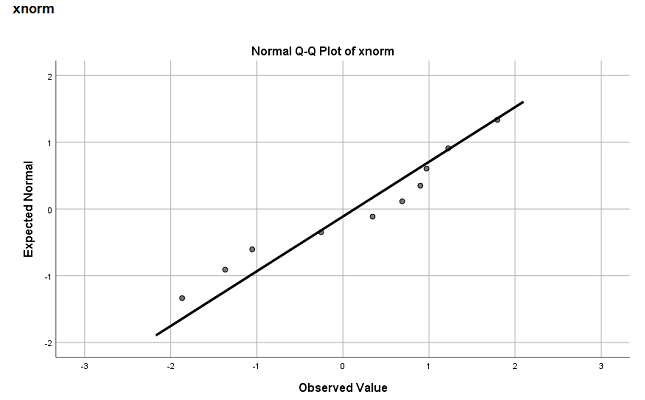
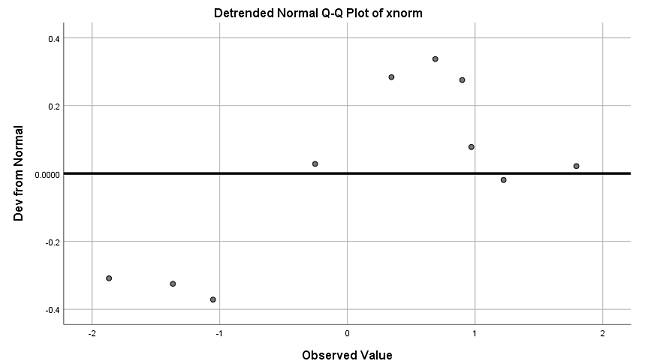
خلاصه و جمع‌بندی

در این نوشتار به بررسی آماره و آزمون شاپیرو ویلک (Shapiro-Wilk Test) پرداختیم و با نحوه محاسبه آن در چند نرم‌افزار محاسبات آماری نظیر R و پایتون آشنا شدیم. مطابق با شبیه‌سازی‌های انجام شده به نظر می‌رسد که استفاده از آماره و آزمون شاپیرو ویلک می‌تواند نتایج دقیق‌تر و صادقانه‌تری نسبت به رد فرض صفر که مطابقت توزیع داده‌ها با توزیع نرمال است در اختیار قرار دهد. ولی به هر حال استفاده از روش‌های تصویری نظیر نمودار چندک-چندک یا Q-Q plot‌ نیز در تصمیم نهایی می‌تواند نقش مهمی داشته باشد.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های نرم‌افزارهای آماری
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های آمار احتمالات و داده‌کاوی
• مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری
• توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها
• توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس