فرادرسرگرسیون لجستیک چند جمله ای (Multinomial Logistic Regression) — مفاهیم و کاربردها
در تجزیه و تحلیل داده‌ها بخصوص «یادگیری نظارت شده» (Supervised Learning) در زمینه «یادگیری ماشین» (Machine Learning)، روش «رگرسیون لجستیک دودویی» (Binary Logistic Regression) و رگرسیون لجستیک چند جمله ای (Multinomial Logistic Regression) نقش مهمی دارند.
این دو روش رگرسیونی، براساس مقادیر کیفی برای متغیر پاسخ عمل می‌کنند و قادر هستند مشاهدات را به کمک مدلی که براساس رابطه بین متغیرهای مستقل (با مقادیر کمی یا کیفی) و متغیر پاسخ (با مقادیر کیفی) می‌سازند، به دو یا چند گروه طبقه‌بندی کنند.
در نوشتارهای دیگر فرادرس مانند رگرسیون لجستیک (Logistic Regression) — مفاهیم، کاربردها و محاسبات در SPSS و رگرسیون لجستیک در پایتون — راهنمای گام به گام با حالتی که متغیر پاسخ دو وضعیتی یا باینری بود، آشنا شدیم. در این نوشتار به بررسی مدلی خواهیم پرداخت که متغیر پاسخ دارای چند سطح باشد و در نتیجه براساس آن مشاهدات به بیش از دو گروه نسبت داده خواهد شد. به این ترتیب می‌توان «رگرسیون لجستیک چند جمله‌ای» (Multinomial Logistic Regression) را حالت کلی‌تری برای «رگرسیون لجستیک باینری» (Binary Logistic Regression) در نظر گرفت.
رگرسیون لجستیک چند جمله ای (Multinomial Logistic Regression)
زمانی که در یک مسئله رگرسیونی، «متغیر پاسخ» (Response Variable) یا «متغیر وابسته» (Dependent Variable) به صورت متغیر طبقه‌ای یا متغیر اسمی باشند، روش تحلیل رگرسیونی به صورت رگرسیون لجستیک چند جمله‌ای است.
برای مشخص شدن صورت چنین مسئله‌هایی به مثال‌های زیر توجه کنید.
- مدل مناسب برای پیش‌بینی رشته انتخابی دانشگاهی، براساس نمره و امتیازات دانش‌آموزان در دبیرستان.
- تعیین رابطه بین گروه خونی افراد و نتایج یک آزمایش پزشکی.
- تعیین مدل مناسب به منظور انتخاب شهرستان مناسب برای ایجاد یک شبعه از فروشگاه‌های زنجیره‌ای.
- تعیین مدل برای تعیین گروه‌هایی از مردم که به کاندیدای خاصی رای می‌دهند.
همانطور که دیده می‌شود، همه این مسائل، به صورت یک موضوع «طبقه‌بندی» (Classification) قابل حل هستند. از آنجایی که رگرسیون لجستیک چند جمله‌ای یکی از ابزارهای حل چنین مسئله‌هایی محسوب می‌شود، در ادامه به بررسی آن خواهیم پرداخت.
فرضیات رگرسیون لجستیک چند جمله‌ای
همانطور که در مدل رگرسیون خطی، فرضیاتی در مورد متغیرهای مستقل و وابسته وجود دارد، در مدل رگرسیون لجستیک چند جمله‌ای نیز باید فرضیاتی را برای شروع کار مورد بررسی قرار داد.
- هر مشاهده فقط با یک مقدار از مقادیر متغیر وابسته، مرتبط است. به این معنی که نمی‌توان برای متغیر پاسخ هر مشاهده بیش از یک مقدار را در نظر گرفت.
- رابطه بین متغیر پاسخ و متغیرهای مستقل، به صورت صریح و کامل نیست و بنابراین باید از الگو‌های تصادفی (وجود جمله خطا) در مدل رگرسیونی استفاده کرد.
- در رگرسیون لجستیک چند جمله‌ای، نسبت بخت‌ها (Odds Ratio) با ورود متغیر غیر مرتبط تغییر نخواهد کرد. این فرض باعث می‌شود که یک مدل رگرسیون لجستیک با k دسته یا گروه را براساس k-1 متغیر دو-دویی یا باینری مستقل، مدل‌سازی کرد.
مدل‌سازی رگرسیون لجستیک چند جمله‌ای با رگرسیون لجستیک باینری
روش‌های مختلفی برای مدل‌سازی رگرسیون لجستیک چند جمله‌ای وجود دارد. ولی در این نوشتار ما به بررسی مدل‌سازی براساس رگرسیون لجستیک باینری یا دو دویی خواهیم پرداخت. در این حالت هدف ایجاد یک تابع خطی از متغیرهای مستقل است که می‌توانند یک تابع امتیاز (Score) را برای هر یک از سطوح متغیر پاسخ ایجاد کنند.
فرض کنید متغیر پاسخ دارای k مقدار متفاوت یا k گروه باشد. به این ترتیب می‌توان تابع امتیاز برای مشاهده iام در گروه k را به صورت زیر در نظر گرفت.
$$ \large \operatorname {score} (\mathbf {X} _{i},k)={\boldsymbol {\beta }}_{k}\cdot \mathbf {X} _{i}$$
مشخص است که منظور از $$X_i$$ بردار از متغیرهای مستقل است. همچنین $$\beta_k$$ نیز بردار وزن‌ها یا همان ضرایب مدل رگرسیونی برای نتیجه گروه kام است. باید توجه داشت که در این رابطه منظور از «.»، ضرب داخلی دو بردار (Dot Product) در نظر گرفته شده است. به این ترتیب این تابع نشان می‌دهد که امتیاز قرارگیری مشاهده $$X_i$$ در گروه kام چقدر است. با توجه به حداکثر مقدار این تابع، مدل رگرسیون لجستیک چند جمله‌ای، مشخص می‌کند که این مشاهده به کدام گروه تعلق دارد.
تفاوت عمده‌ای که مدل رگرسیونی لجستیک چند جمله‌ای نسبت به دیگر روش‌های رده‌بندی مانند الگوریتم پرسپترون (Perceptron Algorithm) یا ماشین بردار پشتیبان (SVM) و ... دارد، استفاده از احتمال برای تعیین وزن‌ها یا تابع امتیاز است. به این معنی که در رگرسیون لجستیک چند جمله‌ای، تابع امتیاز مشخص می‌کند که با چه احتمالی، مشاهده iام در گروه یا رده kام قرار می‌گیرد.
مدل خطی برای متغیرهای مستقل در رگرسیون لجستیک چند جمله‌ای
همانطور که در قبل گفته شد، با استفاده از تابع امتیاز، میزان تعلق هر یک از مشاهدات به گروه kام محاسبه می‌شود. این تابع امتیاز را می‌توان به صورت یک رابطه خطی بین متغیرها و ضرایبشان نوشت.
$$\large score(X_i,k)=\beta _{0,k}+\beta _{1,k}x_{1,i}+\beta _{2,k}x_{2,i}+\cdots +\beta _{M,k}x_{M,i}$$
در اینجا ضریب $$\beta_{j,k}$$ نشانگر، وزن متغیر jام برای تابع امتیاز تعلق مشاهده iام به گروه kام است.
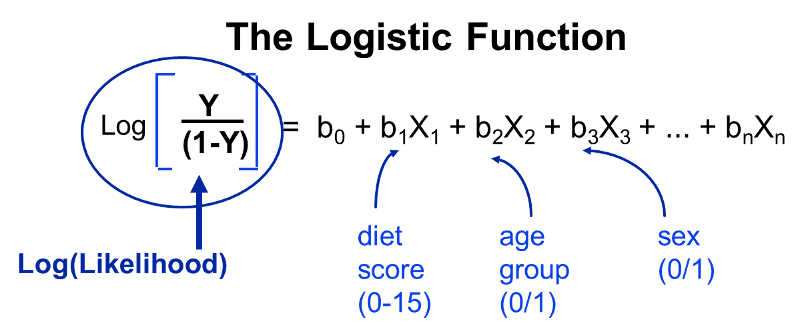
حال به طور جداگانه روشی که برای محاسبه رگرسیون لجستیک باینری به کار می‌رود را برای هر سطح از متغیر پاسخ رگرسیون لجستیک چند جمله‌ای به کار می‌بریم. بنابراین براساس نسبت بخت‌ها داریم:
$$\large \begin{aligned}\ln {\frac {\Pr(Y_{i}=1)}{\Pr(Y_{i}=K)}}&={\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}\\ \large \ln {\frac {\Pr(Y_{i}=2)}{\Pr(Y_{i}=K)}}&={\boldsymbol {\beta }}_{2}\cdot \mathbf {X} _{i}\\ \large \cdots &\cdots \\\ln {\frac {\Pr(Y_{i}=K-1)}{\Pr(Y_{i}=K)}}&={\boldsymbol {\beta }}_{K-1}\cdot \mathbf {X} _{i}\\\end{aligned}$$
حال اگر هر دو طرف تساوی‌های قبلی را به صورت نمایی بنویسیم و عمل طرفین وسطین را اجرا کنیم، نتایج به صورت زیر خواهد بود.
$$\large \begin{aligned}\Pr(Y_{i}=1)&={\Pr(Y_{i}=K)}e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}\\ \large \Pr(Y_{i}=2)&={\Pr(Y_{i}=K)}e^{{\boldsymbol {\beta }}_{2}\cdot \mathbf {X} _{i}}\\ \large \cdots &\cdots \\\Pr(Y_{i}=K-1)&={\Pr(Y_{i}=K)}e^{{\boldsymbol {\beta }}_{K-1}\cdot \mathbf {X} _{i}}\\\end{aligned}$$
از آنجایی که مجموعه احتمالات تعلق هر مشاهده به k گروه برابر با ۱ است می‌توان نوشت:
$$ \large \Pr(Y_{i}=K)=1-\sum _{k=1}^{K-1}\Pr(Y_{i}=k)=1-\sum _{k=1}^{K-1}{\Pr(Y_{i}=K)}e^{{\boldsymbol {\beta }}_{k}\cdot \mathbf {X} _{i}}\\ \large \Rightarrow \Pr(Y_{i}=K)={\frac {1}{1+\sum _{k=1}^{K-1}e^{{\boldsymbol {\beta }}_{k}\cdot \mathbf {X} _{i}}}}$$
به این ترتیب مقدار احتمال قرارگیری هر مشاهده به هر یک از گروه‌ها به صورت زیر قابل محاسبه است.
$$\large {\begin{aligned}\Pr(Y_{i}=1)&={\frac {e^{{\boldsymbol {\beta }}_{1}\cdot \mathbf {X} _{i}}}{1+\sum _{k=1}^{K-1}e^{{\boldsymbol {\beta }}_{k}\cdot \mathbf {X} _{i}}}}\\ \large \Pr(Y_{i}=2)&={\frac {e^{{\boldsymbol {\beta }}_{2}\cdot \mathbf {X} _{i}}}{1+\sum _{k=1}^{K-1}e^{{\boldsymbol {\beta }}_{k}\cdot \mathbf {X} _{i}}}}\\ \large \cdots &\cdots \\ \large \Pr(Y_{i}=K-1)&={\frac {e^{{\boldsymbol {\beta }}_{K-1}\cdot \mathbf {X} _{i}}}{1+\sum _{k=1}^{K-1}e^{{\boldsymbol {\beta }}_{k}\cdot \mathbf {X} _{i}}}}\\\end{aligned}}$$
برای پیدا کردن ضرایب مدل رگرسیون لجستیک چند جمله‌ای نمی‌توان روش صریحی ارائه کرد و با استفاده از تکنیک‌های بهینه‌سازی مانند روش بهینه‌سازی «گردایان کاهشی» (Gradianet Descent) این کار صورت می‌گیرد.
خلاصه و جمع‌بندی
هانطور که تا به حال دیدید، هنگام استفاده از رگرسيون لجستيک چند جمله‌ای، يک دسته متغير وابسته به عنوان رده مرجع انتخاب شده است. نسبت‌های شانس جداگانه برای همه متغیرهای مستقل برای هر دسته از متغیر وابسته به استثنای رده مرجع، که از تجزیه و تحلیل حذف شده است، تعیین می‌شود. ضریب $$\beta$$، نشانگر تغییر در شانس متغیر وابسته با تغییر یک واحد از متغیر مستقل در نظر گرفته می‌شود.
در پردازش زبان طبیعی، رگرسیون چند جمله‌ای به عنوان یک «دسته‌بند» (Classifier) می‌تواند جایگزین مناسبی برای Naive Bayes باشد زیرا در آنجا به استقلال آماری متغیرها توجهی نمی‌شود. البته به علت استفاده از الگوریتم‌های بهینه‌سازی معمولا رگرسیون لجستیک چند جمله‌ای، با سرعت کمتری نسبت به Naive Bayes اجرا می‌شود، بنابراین برای مدل‌سازی روی داده‌های حجیم پیشنهاد نمی‌شود.
اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزش های SPSS
- مجموعه آموزش های داده کاوی یا Data Mining در متلب
- آموزش همبستگی و رگرسیون خطی در SPSS
- مجموعه آموزش‌های یادگیری ماشین و بازشناسی الگو
- ضریب‌های همبستگی (Correlation Coefficients) و شیوه محاسبه آن‌ها
- مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری
- رگرسیون لجستیک (Logistic Regression) — مفاهیم، کاربردها و محاسبات در SPSS
- رگرسیون لجستیک در پایتون — راهنمای گام به گام
^^
سلام و تشكر از مباحث آموزشي بسيار ارزشمند شما
سوالي داشتم. مي خواستم بدانم علاوه بر تعيين جداگانه نسبت هاي شانس متغييرهاي مستقل در هر دسته از متغيير هاي وابسته ، آيا امكان استخراج معادله رگرسيون لجستيك چند جمله اي توسط نرم افزار spss و يا ديگر نرم افزارها وجود دارد؟