رگرسیون خطی با گرادیان کاهشی (Gradient Descent) – پیاده سازی با پایتون

«رگرسیون» (Regression) یکی از کارآمدترین ابزارهای تحلیل چند متغیره است که بخصوص در «یادگیری ماشین» (Machine Learning) کاربرد زیادی دارد. مدل «رگرسیون خطی ساده» (Simple Linear Regression) دارای دو پارامتر «عرض از مبدا» (Intercept)  و «شیب خط« (Slope) است. در این مطلب به بررسی برآورد پارامترهای مدل رگرسیون خطی ساده و پیاده‌سازی آن در «پایتون» (Python) می‌پردازیم.

در این نوشتار، ابتدا با تکنیک رگرسیون خطی آشنا شده، سپس «تابع زیان» (Loss Function) را معرفی می‌کنیم. در انتها نیز با الگوریتم «گرادیان کاهشی» (Gradient Descent) و شیوه عملکرد آن برای پیدا کردن پارامترهای مدل رگرسیون مطلب را خاتمه می‌دهیم. برای انجام محاسبات نیز از زبان برنامه‌نویسی پایتون استفاده خواهیم کرد.

به عنوان مقدمه و آشنایی با تکنیک رگرسیون خطی ساده می‌توانید مطلب رگرسیون خطی — مفهوم و محاسبات به زبان ساده را مطالعه کنید. همچنین برای آگاهی از مفهوم تابع زیان و انواع آن، مطالعه نوشتار تابع زیان (Loss Function) در یادگیری ماشین – به همراه کدهای پایتون خالی از لطف نیست.

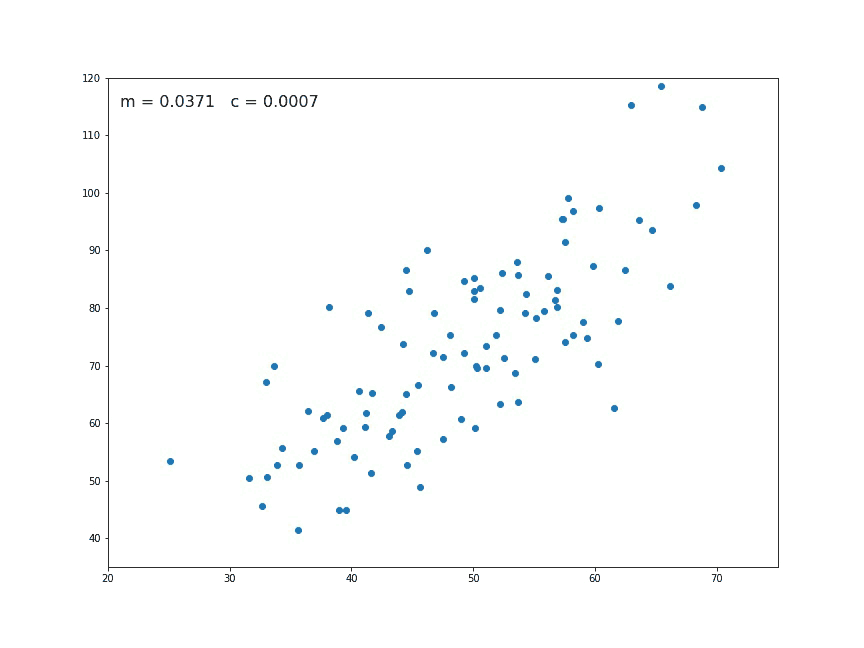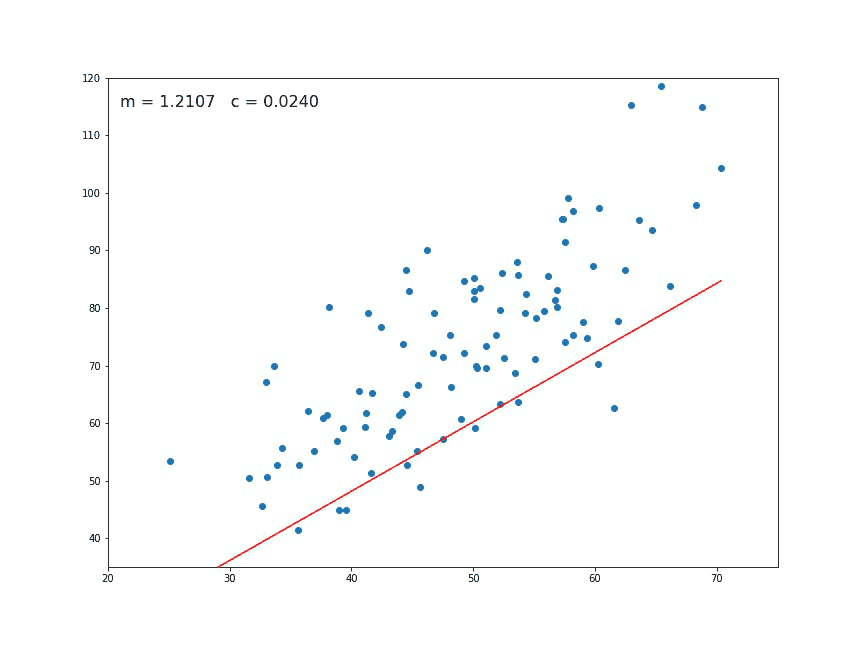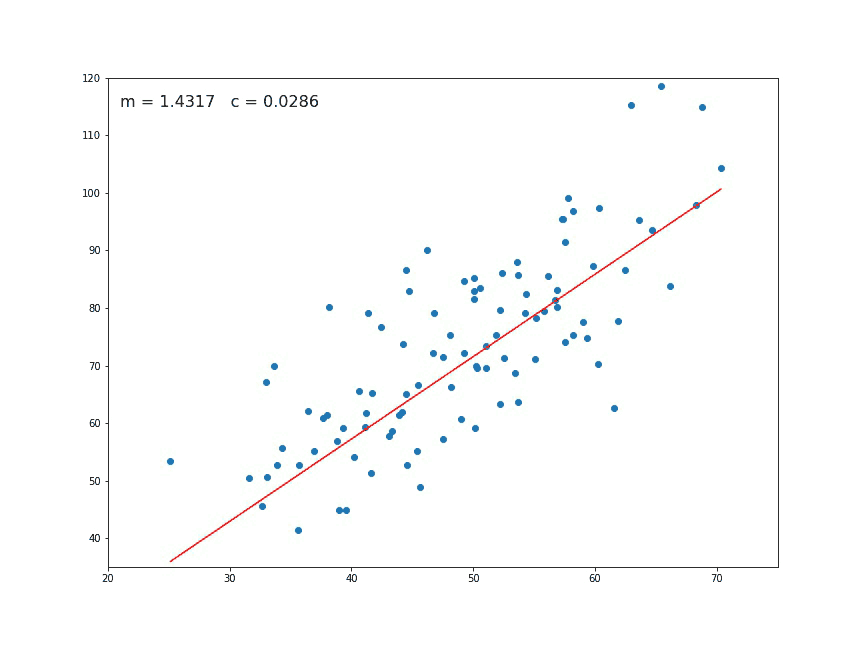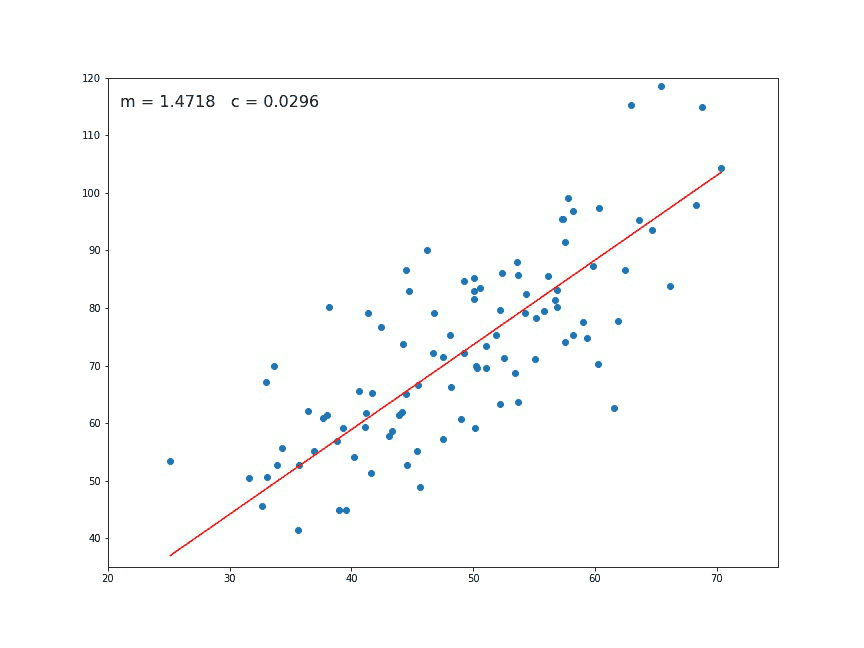
رگرسیون خطی به کمک گرادیان کاهشی

در آمار، رگرسیون خطی یک روش تحلیل چند متغیره برای پیدا کردن رابطه خطی بین «متغیر پاسخ» (Response) و یک یا چند «متغیر مستقل» (Independent) است.

فرض کنید که X متغیر مستقل یا توصیفی و Y نیز متغیر پاسخ باشد. رابطه خطی بین این دو متغیر را به صورت زیر می‌نویسم:

$$Y=mX+c$$

همانطور که در مطالب فرادرس با موضوع معادله خط خوانده‌اید، می‌دانید که m بیانگر «شیب» (Slope) یا «ضریب متغیر» (Coefficient) و c نیز «عرض از مبدا» (Intercept) نامیده می‌شود.

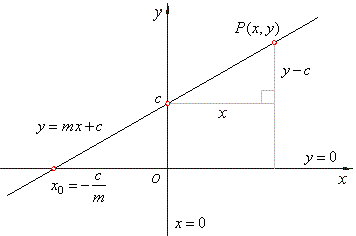
در این نوشتار، مدل پیش‌بینی را به کمک معادله این خط براساس داده‌های موجود آموزش می‌دهیم سپس از مدل بدست آمده برای پیش‌بینی مقدارهای Y برحسب X استفاده می‌کنیم. در اینجا منظور از آموزش مدل توسط داده‌ها و معادله خط، پیدا کردن پارامترهای معادله خط یعنی m و c است. به این ترتیب معادله خط کامل شده و می‌توان به ازای مقدارهای مختلف X، مقدار Y را با کمترین خطا پیش‌بینی کرد.

تابع زیان (Loss Function)

در اینجا تابع زیان همان میزان خطا است که به پارامترهای m و c بستگی دارد. هدف ما پیدا کردن معادله خطی است که کمترین خطا یا زیان را نسبت به مقدارهای واقعی m و c دارد. در این نوشتار از تابع زیان «میانگین مربعات خطا» (Mean Squared Error) برای محاسبه زیان و برآورد پارامترها استفاده می‌کنیم.

فیلم آموزش رگرسیون لجستیک در یادگیری ماشین (رایگان) در فرادرس

کلیک کنید

برای محاسبه میانگین مربعات خطا سه مرحله محاسباتی لازم است:

1. پیدا کردن فاصله یا اختلاف بین مقدار واقعی Y و پیش‌بینی آن یعنی $$\hat{Y}$$ که توسط معادله خط $$\hat{Y}=mX+c$$ صورت می‌گیرد. به این ترتیب این فاصله به صورت $$Y-\hat{Y}$$ بدست می‌آید.
2. محاسبه مربع یا توان دوم نتیجه حاصل از مرحله ۱ برای همه مشاهدات در این مرحله صورت می‌گیرد.
3. محاسبه میانگین مقدارهای حاصل از مرحله ۲ که در زیر دیده می‌شود.

$$\large E=\dfrac{1}{n}\sum_{i=1}^n(Y_i-\hat{Y}_i)^2$$

در رابطه بالا، E تابع زیان و n نیز تعداد مشاهدات یا داده‌ها است. همچنین منظور از $$\hat{Y}_i$$ نیز مقدار پیش‌بینی شده توسط مدل خطی است. حال فرض کنید مقدار $$\hat{Y}_i$$ توسط رابطه خط جایگزین شود. در نتیجه خواهیم داشت:

$$\large E=\dfrac{1}{n}\sum_{i=1}^n(Y_i-(mX_i+c))^2$$

به این ترتیب، خطا را به توان ۲ رسانده و مجموع آن‌ها را محاسبه می‌کنیم. در نهایت نیز باید میانگین آن‌ها را هم بدست آوریم. حال که تابع زیان به دست آمده است، باید مقدار پارامترها یعنی m  و c را طوری انتخاب کنیم که تابع زیان حداقل ممکن باشد.

نکته: باید توجه داشت که الگوریتم گرادیان کاهشی برای تابع زیان‌هایی مقدار کمینه را محاسبه می‌کند که «محدب» (Convex) باشند.

الگوریتم گرادیان کاهشی

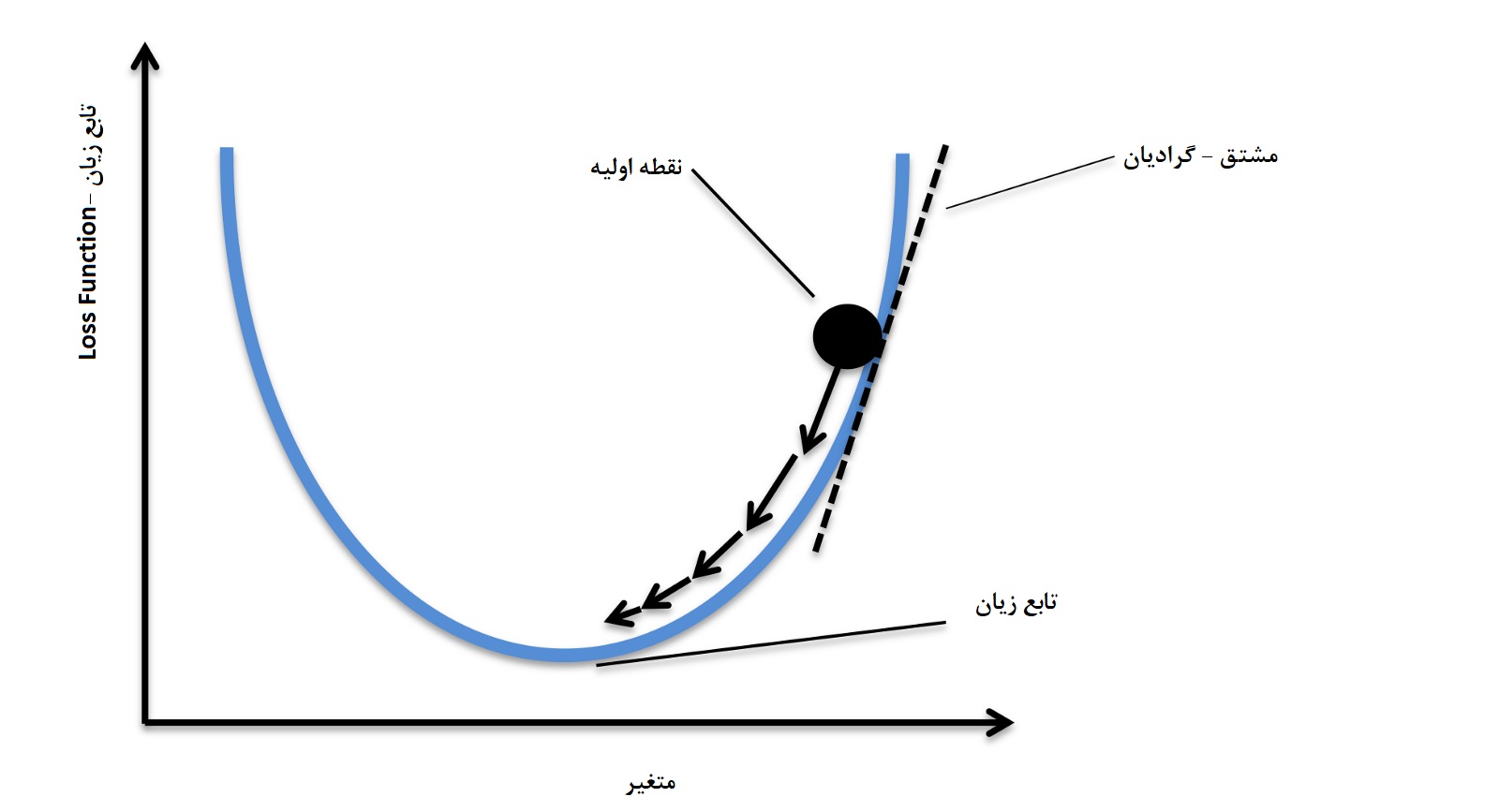
گرادیان کاهشی یک الگوریتم بهینه‌سازی تکرارپذیر است که به کمک آن می‌توان مقدار کمینه یک تابع مورد نظر را محاسبه کرد. در اینجا تابع مورد نظر، همان تابع زیان است.

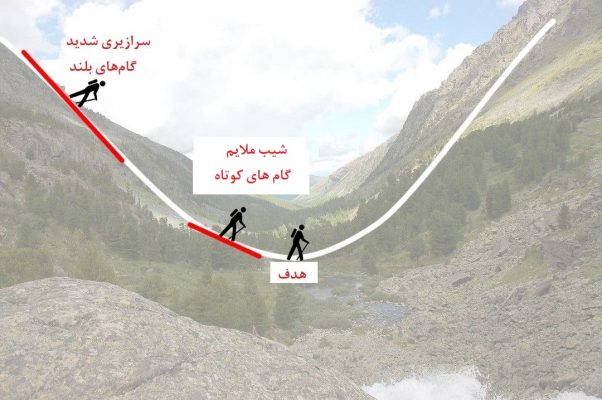
تصور کنید که در کوهستان مشغول پیاده روی هستید و می‌خواهید از ستیغ کوه به دره برسید ولی به علت مه آلود بودن هوا متوجه نمی‌شوید که چه موقعی به دره رسیده‌اید. از شیب زمین و سرازیری کمک می‌گیرد. از سرازیری به پایین می‌آیید. در ابتدای راه گام‌های شما بلند است زیرا می‌دانید که هدف (دره) دور از شما قرار دارد و احتیاج به دقت در تشخیص موقعیت خود ندارید. ولی زمانی که شیب ملایم می‌شود می‌فهمید که به دره نزدیک شده‌اید و باید گام‌‌هایتان را کوتاه بردارید تا دره را پیدا کنید.

به این ترتیب در هر گام، موقعیت بعدیتان را براساس موقعیت فعلی تنظیم می‌کنید تا از مسیر خارج نشوید. به این شیوه مشخص است که گام بعدی شما به گام قبلی بستگی دارد. در این حالت کاهش طول گام‌ها را با کاهش شیب هماهنگ می‌کنید تا زمانی که دیگر شیبی وجود ندارد. در این هنگام به دره که هدفتان بود، رسیده‌اید.

این عملکرد همان چیزی است که در الگوریتم گرادیان کاهشی رخ می‌دهد. در ادامه، این الگوریتم را برای پیدا کردن پارامترهای m و c، قدم به قدم به کار می‌گیریم.

۱- مقدار دهی اولیه: فرض کنید m و c موقعیت شما را تعیین می‌کنند. به عنوان مقدارهای اولیه m=0 و c=0 در نظر گرفته می‌شود. در این میان L را نیز نرخ یادگیری می‌نامیم. مقدار L نشان می‌دهد که میزان تغییر m در هر مرحله چقدر است. امیدواریم تغییر در مقدار m در آخرین مراحل اجرای الگوریتم گرادیان کاهشی، ما را به هدف که کمینه‌سازی تابع زیان است، برساند.

۲- محاسبه مشتق: مشتق جزئی تابع زیان را برحسب m که ضریب X است، محاسبه می‌کنیم و آن را $$D_m$$ می‌نامیم. در این حالت چون این مشتق برابر با $$-X_i$$ است، داریم:

$$D_m=\frac{-2}{n}\sum_{i=1}^n (X_i)(Y_i-\hat{Y}_i)$$

به همین ترتیب مشتق جزئی تابع زیان را نسبت به c محاسبه می‌کنیم و آن را $$D_c$$ می‌نامیم. به این ترتیب خواهیم داشت:

$$D_c=\frac{-2}{n}\sum_{i=1}^n (Y_i-\hat{Y}_i)$$

3- به روز رسانی پارامترها:  براساس رابطه زیر مقدار پارامترها را در این مرحله به روز می‌کنیم.

$$m=m-L\times D_m$$

$$c=c-L\times D_c$$

4- تکرار مراحل: با جایگزینی مقدار m و c‌ حاصل شده در هر مرحله، مقدار $$\hat{Y}$$ محاسبه می‌شود و مجدد مقدار مشتقات جزئی تابع زیان براساس محاسبات جدید به روز خواهد شد. این گام‌ها تا زمانی که مقدار تابع زیان بسیار کوچک شده باشد، ادامه پیدا می‌کند. در حالت ایده‌آل باید مقدار تابع زیان صفر شود که در این حالت، دقت ۱۰۰٪ در پیش‌بینی رخ خواهد داد و این وضعیت فقط زمانی پیش خواهد آمد که دقیقا مقدارهای $$X$$ و $$Y$$ روی یک خط راست قرار گرفته باشند.

حال به مسئله کوهنوردی شما بر می‌گردیم. فرض کنید m و c موقعیت شما را نشان می‌دهند. مشتق جزئی یعنی $$D_m$$ نیز میزان شیب یا سرازیری را نشان می‌دهد. از طرف دیگر می‌توان L را سرعت حرکت شما در نظر گرفت. در این حالت مقدار جدید m در طرف چپ مرحله ۳ نشان‌دهنده موقعیت بعدی شما است و $$L\times D$$ نیز طول گام‌های شما را نشان می‌دهد. وقتی که شیب یعنی مقدار D بزرگ باشد، شما گام‌های بلندی بر می‌دارید زیرا می‌دانید که هدف در دور دست است. وقتی که شیب کم می‌شود، طول گام‌ها شما کوتاه می‌شود زیرا می‌دانید که در حال نزدیک شدن به دره هستید. در انتها نیز زمانی که شیب صفر است دیگر تغییر مکانی نخواهید داشت پس مقدار m و c انتهایی موقعیت شما را در دره نشان می‌دهند.

پیاده سازی برآورد پارامترهای مدل رگرسیون خطی با گرادیان کاهشی در پایتون

ابتدا اجازه دهید که محیط را برای انجام محاسبات آماده سازیم.

# Making the imports
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (12.0, 9.0)

# Preprocessing Input data
data = pd.read_csv('data.csv')
X = data.iloc[:, 0]
Y = data.iloc[:, 1]
plt.scatter(X, Y)
plt.show()

همانطور که مشخص است در این قسمت از کد، ابتدا کتابخانه‌ها و سپس منبع اطلاعاتی data معرفی شده‌اند.

نگته: برای دریافت فایل‌های کد و همچنین فایل اطلاعاتی می‌تواند از لینک (+) استفاده کنید.

دستور $$plt.scatter(X,Y)$$ برای ترسیم نموداری که به نام «نمودار نقطه‌ای پراکندگی» (Scatter-Dot Plot) معروف است به کار رفته تا رابطه بین دو متغیر X و Y مخشص شود. با اجرای فرمان $$plt.show()$$ این نمودار نمایش داده می‌شود.

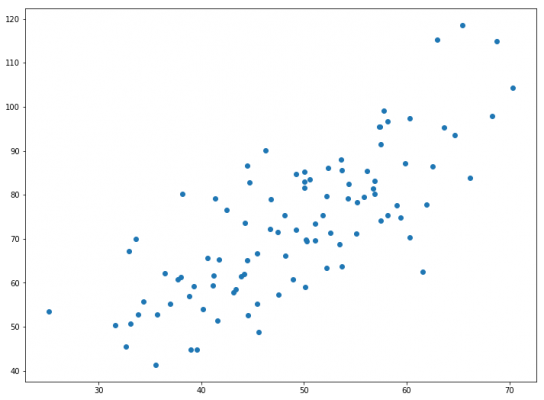
کدهایی که در ادامه دیده می‌شوند به منظور برآورد پارامترها و استفاده از گرادیان کاهشی نوشته شده است.

# Building the model
m = 0
c = 0

L = 0.0001  # The learning Rate
epochs = 1000  # The number of iterations to perform gradient descent

n = float(len(X)) # Number of elements in X

# Performing Gradient Descent 
for i in range(epochs): 
    Y_pred = m*X + c  # The current predicted value of Y
    D_m = (-2/n) * sum(X * (Y - Y_pred))  # Derivative wrt m
    D_c = (-2/n) * sum(Y - Y_pred)  # Derivative wrt c
    m = m - L * D_m  # Update m
    c = c - L * D_c  # Update c
    
print (m, c)

همانطور که مشخص است مقدار دقت یا نرخ یادگیری L=0.0001 در نظر گرفته شده است. مقدارهای اولیه برای m و c نیز صفر هستند. متغیر epochs=1000 تعداد تکرار الگوریتم برای رسیدن به مقدار کمینه تابع زیان را مشخص کرده است. تکرارها و محاسبات مربوط به گرادیان کاهشی نیز در حلقه تکرار نوشته شده‌اند. در انتها مقدار پارامترهای مدل خطی یعنی m و c ظاهر می‌شوند. براساس داده‌های مربوطه، برآوردها به صورت زیر خواهند بود.

1.4796491688889395 0.10148121494753726

در اینجا، اولین مقدار، شیب (m) و دومین مقدار، عرض از مبدا (c) است. برای نمایش معادله خط بر روی نمودار نقطه‌ای از کد دستوری plt.plot کمک گرفته‌ایم. به این ترتیب کدهای زیر نمودار نقطه‌ای به همراه خط رگرسیونی را نشان می‌دهند

# Making predictions
Y_pred = m*X + c

plt.scatter(X, Y) 
plt.plot([min(X), max(X)], [min(Y_pred), max(Y_pred)], color='red')  # regression line
plt.show()

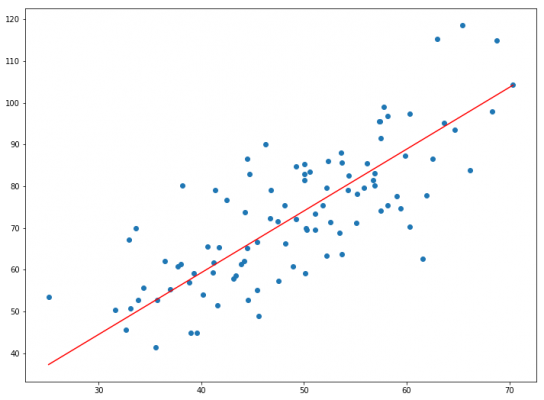
گردیان کاهشی یکی از ساده‌ترین و در عین حال عمومی‌ترین الگوریتم‌هایی است که در یادگیری ماشین به کار می‌رود. بنابراین آشنایی، یادگیری و به کارگیری آن از اساس و پایه‌های اصلی تحلیل داده‌ها و یادگیری ماشین است.

اگر نوشته بالا برای شما مفید بوده، آموزش‌ها و مطالبی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های هوش محاسباتی
• مجموعه آموزش‌های شبکه‌های عصبی مصنوعی
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• گنجینه آموزش‌های برنامه نویسی پایتون (Python)
• معرفی منابع جهت آموزش یادگیری عمیق (Deep Learning) — راهنمای کامل
• معرفی منابع آموزش ویدئویی هوش مصنوعی به زبان فارسی و انگلیسی
• گرادیان کاهشی (Gradient Descent) و پیاده سازی آن در پایتون — راهنمای کاربردی

^^