نقاط تعادل سیستم خطی — راهنمای جامع

نقاط تعادل در یک سیستم خطی خودگردان (Equilibrium Points of Linear Autonomous System) یکی از مهم‌ترین مباحثی است که در تحلیل پایداری سیستم‌ها و نیز کنترل آن‌ها مورد بررسی قرار می‌گیرد. در این آموزش قصد داریم به بررسی انواع مختلف نقاط پایداری یک سیستم خطی مستقل بپردازیم و ویژگی‌های هر یک را بیان کنیم.

ابتدا یک سیستم خطی همگن مرتبه دوم با ضرایب ثابت را در نظر بگیرید که توسط معادلات زیر توصیف شده است:

$$\left\{ \begin{array}{l} \frac{{dx}}{{dt}} = {a_{11}}x + {a_{12}}y\\ \frac{{dy}}{{dt}} = {a_{21}}x + {a_{22}}y \end{array} \right..$$

این دستگاه معادلات، مستقل است؛ زیرا سمت راست معادلات به صورت صریح شامل متغیر مستقل t نیست. دستگاه معادلات بالا را در فرم ماتریسی می‌توان به صورت زیر بازنویسی کرد:

$${\mathbf{X’} = A\mathbf{X},\;\;\text{where}\;\;\mathbf{X} = \left[ {\begin{array}{*{20}{c}}<br /> x\\<br /> y<br /> \end{array}} \right],\;\;}\kern0pt<br /> {A = \left[ {\begin{array}{*{20}{c}}<br /> {{a_{11}}}&{{a_{12}}}\\<br /> {{a_{21}}}&{{a_{22}}}<br /> \end{array}} \right].} $$

حال نقاط تعادل را در این سیستم می‌توان با حل کردن معادله زیر به دست آورد:

$$A\mathbf{X} = \mathbf{0}.$$

در این معادله اگر ماتریس A ناتکین (Nonsingular) باشد، فقط یک حل یکتا $$\mathbf{X} = \mathbf{0}$$ دارد.

فیلم آموزش تحلیل سیستم های غیر خطی در فرادرس

کلیک کنید

ماتریس ناتکین، ماتریسی است که مقدار دترمینان آن مخالف صفر باشد. اما اگر ماتریس A تکین (Singular) باشد، در این صورت دستگاه معادلات بی نهایت جواب یا نقطه تعادل دارد.

طبقه بندی نقاط تعادل بر اساس مقادیر ویژه ماتریس A، یعنی $$\lambda_1$$ و $$\lambda_2$$ انجام می‌گیرد. این اعداد ویژه را می‌توان با حل معادله کمکی زیر به دست آورد:

$${\lambda ^2} – \left( {{a_{11}} + {a_{22}}} \right)\lambda + {a_{11}}{a_{22}} – {a_{12}}{a_{21}} = 0.$$

زمانی که ماتریس A ناتکین باشد، می‌توان گفت که ۴ نوع نقطه تعادل مختلف وجود دارد.

• نقطه تعادل گره (Node): در این حالت مقادیر ویژه، هر دو عدد حقیقی و دارای علامت یکسانی هستند ($$\lambda_1 . \lambda _2 >0$$).
• نقطه تعادل زینی (Saddle): در این نوع از نقاط تعادل، مقادیر ویژه عدد حقیقی و غیر صفر بوده و علامت‌های آن‌ها مخالف با یکدیگر است ($$\lambda_1 . \lambda _2 <0$$).
• نقطه تعادل کانونی (Focus): در این حالت، مقادیر ویژه اعداد مختلط بوده و بخش حقیقی آن‌ها با یکدیگر برابر و نیز غیر صفر است ($$RE\; \lambda_1 = RE \; \lambda _2$$).
• نقطه تعادل مرکزی (Center): در این نوع نقطه تعادل، مقادیر ویژه اعداد کاملا موهومی هستند ($$RE\; \lambda_1 = RE \; \lambda _2 =0$$).

پایداری نقاط تعادل توسط قضیه عمومی پایداری تعیین می‌شود. بر اساس این قضیه، اگر مقادیر ویژه حقیقی و یا قسمت حقیقی در مقادیر ویژه موهومی، منفی باشند، آن‌‌گاه می‌توان گفت که آن نقطه تعادل پایدار مجانبی (Asymptotically Stable) است. نقاط تعادل گره و کانونی نمونه‌های از چنین نقاط تعادلی محسوب می‌شوند.

اگر قسمت حقیقی در حداقل یکی از مقادیر ویژه مثبت باشد، آن‌گاه نقطه تعادل متناظر با آن مقادیر ویژه ناپایدار (Unstable) است. این نقطه تعادل مثلا می‌تواند یک نقطه زینی باشد.

نهایتا در مورد مقادیر ویژه موهومی که در آن نقطه تعادل را مرکزی می‌نامند، با یک مسئله کلاسیک در تئوری پایداری لیاپانوف (Lyapunov) رو به رو می شویم.

هدف بعدی در بررسی نقاط تعادل یک سیستم این است که تعیین کنیم رفتار سیستم در نقاط نزدیک به نقطه تعادل به چه صورت خواهد بود. در یک سیستم مرتبه دوم، تعیین این رفتار از طریق نمودارهای گرافیکی که پرتره فاز (Phase Portrait) نام دارند، بسیار آسان است. پرتره فاز یک مجموعه از مسیرهای فاز (Phase Trajectories) در صفحه مختصات است. جهت فلش‌ها در یک مسیر فاز نشان‌دهنده جهت حرکت نقطه و یا حالت خاصی در سیستم در طول زمان هستند. حال به بررسی چنین نقاطی در سیستم‌های مختلف و پرتره فاز متناظر با آن‌ها می‌پردازیم.

نقاط تعادل نوع گره پایدار و ناپایدار

مقادیر ویژه $$\lambda_1$$ و $$\lambda _2$$ متناظر با نقطه تعادل نوع گره، در شرایط زیر صدق می‌کنند.

$${\lambda _1},{\lambda _2} \in \Re,\;\;{\lambda _1} \cdot {\lambda _2} \gt 0.$$

فیلم آموزش سیستم های کنترل غیر خطی با رویکرد حل مساله در فرادرس

کلیک کنید

اما در این حالت ممکن است شرایط خاص زیر به وجود بیاید.

مقادیر ویژه $$\lambda_1$$ و $$\lambda_2$$ متمایز ($$\lambda_1 \neq \lambda _2$$) و منفی ($$\lambda_1 < 0 , \lambda _2 < 0$$) هستند. 

حال می‌خواهیم پرتره فاز چنین سیستمی را ترسیم کنیم. ابتدا فرض می‌کنیم که $$\left| {{\lambda _1}} \right| \lt \left| {{\lambda _2}} \right|$$ باشد. حل عمومی معادله فرمی به صورت زیر دارد:

$$\mathbf{X}\left( t \right) = {C_1}{e^{{\lambda _1}t}}{\mathbf{V}_1} + {C_2}{e^{{\lambda _2}t}}{\mathbf{V}_2},$$

که در آن $${\mathbf{V}_1} = {\left( {{V_{11}},{V_{21}}} \right)^T}$$ و $${\mathbf{V}_2} = {\left( {{V_{12}},{V_{22}}} \right)^T}$$ بردارهای ویژه متناظر با مقادیر ویژه هستند و $$C_1$$ و $$C_2$$ ضرایب اختیاری (Arbitrary) هستند.

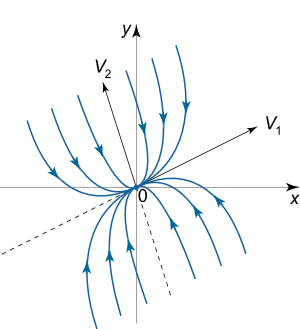
به دلیل این که هر دو مقدار ویژه منفی هستند، در نتیجه می‌توان گفت پاسخ  $$\mathbf{X} = \mathbf{0}$$ پایدار مجانبی است. این نوع نقطه تعادل یک نقطه تعادل گره نام دارد. در این نوع از نقاط تعادل اگر $$t \to \infty$$، آن‌گاه منحنی‌های فاز به سمت مبدا یعنی $$\mathbf{X} = \mathbf{0}$$ میل خواهند کرد.

حال باید جهت مسیرهای فاز را تعیین کنیم. در این سیستم معادله زیر برقرار است:

$${x\left( t \right) = {C_1}{V_{11}}{e^{{\lambda _1}t}} + {C_2}{V_{12}}{e^{{\lambda _2}t}},\;\;}\kern0pt$$

مقدار مشتق $$\large\frac{{dy}}{{dx}}\normalsize$$ به صورت زیر به دست می‌آید:

$${\frac{{dy}}{{dx}} \text{ = }}\kern0pt{\frac{{{C_1}{V_{21}}{\lambda _1}{e^{{\lambda _1}t}} + {C_2}{V_{22}}{\lambda _2}{e^{{\lambda _2}t}}}}{{{C_1}{V_{11}}{\lambda _1}{e^{{\lambda _1}t}} + {C_2}{V_{12}}{\lambda _2}{e^{{\lambda _2}t}}}}.}$$

در معادله بالا صورت و مخرج کسر را بر مقدار $${{e^{{\lambda _1}t}}}$$ تقسیم می‌کنیم:

$${\frac{{dy}}{{dx}} \text{ = }}\kern0pt{\frac{{{C_1}{V_{21}}{\lambda _1} + {C_2}{V_{22}}{\lambda _2}{e^{\left( {{\lambda _2} – {\lambda _1}} \right)t}}}}{{{C_1}{V_{11}}{\lambda _1} + {C_2}{V_{12}}{\lambda _2}{e^{\left( {{\lambda _2} – {\lambda _1}} \right)t}}}}.}$$

در این مورد $${\lambda _2} – {\lambda _1} \lt 0$$ است. در نتیجه عبارتی که شامل تابع نمایی است، زمانی که ‌‌$$t \to \infty$$ به سمت صفر می‌کند. در نهایت در $${C_1} \ne 0$$ معادله زیر به دست می‌آید:

$$\lim\limits_{t \to \infty } \frac{{dy}}{{dx}} = \frac{{{V_{21}}}}{{{V_{11}}}}.$$

بنا بر معادله بالا مسیرهای فاز زمانی که $$t \to \infty$$ با بردار ویژه $${\mathbf{V}_1}$$ موازی می‌شوند.

اگر $${C_1} = 0$$ باشد، آن‌گاه مشتق در تمام زمان‌ها برابر با مقدار زیر خواهد بود:

$$\frac{{dy}}{{dx}} = \frac{{{V_{22}}}}{{{V_{12}}}},$$

به عبارت دیگر می‌توان گفت که مسیرهای فاز بر روی خطوطی هستند که در راستای بردار ویژه $${\mathbf{V}_2}$$ قرار گرفته‌اند.

حال می‌خواهیم رفتار مسیرهای فاز را زمانی که $$t \to -\infty$$ در نظر بگیریم. واضح است که مختصات $$x\left( t \right)$$ و $$y\left( t \right)$$ به سمت بی نهایت میل می‌کنند و مشتق $$\large\frac{{dy}}{{dx}}\normalsize$$ در $${C_2} \ne 0$$ به فرم زیر خواهد بود:

$${\frac{{dy}}{{dx}} \text{ = }}\kern0pt{\frac{{{C_1}{V_{21}}{\lambda _1}{e^{\left( {{\lambda _1} – {\lambda _2}} \right)t}} + {C_2}{V_{22}}{\lambda _2}}}{{{C_1}{V_{11}}{\lambda _1}{e^{\left( {{\lambda _1} – {\lambda _2}} \right)t}} + {C_2}{V_{12}}{\lambda _2}}} }={ \frac{{{V_{22}}}}{{{V_{12}}}},}$$

به این دلیل است که می‌توان گفت مسیرهای فاز در بی نهایت با بردار $${\mathbf{V}_2}$$ موازی می‌شوند. به همین ترتیب زمانی که $${C_2} = 0$$ باشد، مشتق به صورت فرمول زیر خواهد بود:

$$\frac{{dy}}{{dx}} = \frac{{{V_{21}}}}{{{V_{11}}}}.$$

در این حالت مسیرهای فاز توسط جهت بردار ویژه $${\mathbf{V}_1}$$ تعیین می‌شوند. با استفاده از مشخصه‌های بالا برای مسیرهای فاز، پرتره فاز یک نقطه تعادل نوع گره پایدار به صورت زیر خواهد بود.

به طریق مشابه می‌توانیم رفتار مسیرهای فاز برای نوع دیگر نقاط تعادل را نیز بررسی کنیم. به علاوه، اگر از جزئیات صرف نظر کنیم، مشخصه‌های کیفی اساسی نقاط تعادل دیگر را نیز می‌توان به دست آورد.

مقادیر ویژه $$\lambda_1$$ و $$\lambda _2$$ متمایز $$\left( {{\lambda _1} \ne {\lambda _2}} \right)$$ و مثبت $$\left( {{\lambda _1} \gt 0, {\lambda _2}} \gt 0\right)$$ باشند. 

در این حالت، نقطه $$\mathbf{X} = \mathbf{0}$$ یک نقطه گره ناپایدار است. پرتره فاز این نوع نقطه تعادل به صورت زیر ترسیم می‌شود.

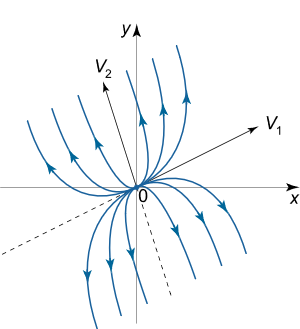
توجه کنید که هم در نقاط تعادل پایدار و هم نقاط تعادل ناپایدار، مسیرهای فاز در امتداد خطی خواهند بود که متناظر با کوچک‌ترین (کوچک‌ترین نه به لحاظ علامت بلکه به لحاظ قدر مطلق) مقدار ویژه است.

گره Dicritical

فرض کنید که معادله کمکی دارای دو ریشه یکسان با مقدار برابر با ۰ باشد ($${\lambda _1} = {\lambda _2} = {\lambda} \ne 0$$). فرض کنید مرتبه تکرار مقادیر ویژه ۲ باشد. به عبارت دیگر ابعاد فضای ویژه ۲ است. این حالت در سیستمی اتفاق می‌افتد که دارای معادلاتی به صورت زیر باشد:

$${\frac{{dx}}{{dt}} = \lambda x,}\;\; {\frac{{dy}}{{dt}} = \lambda y.}$$

جهت مسیرهای فاز به علامت مقادیر ویژه بستگی دارد. به همین دلیل برای این حالت، دو گروه زیر را در نظر می‌گیریم:

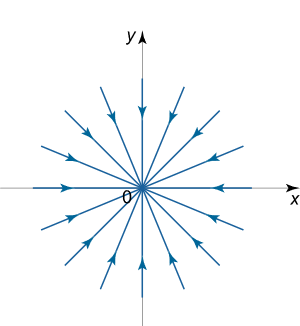
• حالت اول: $${\lambda _1} = {\lambda _2} = {\lambda} \lt 0$$

در این حالت نقطه تعادل را گره پایدار Dicritical می‌نامیم. پرتره فاز چنین سیستمی به صورت شکل زیر است.

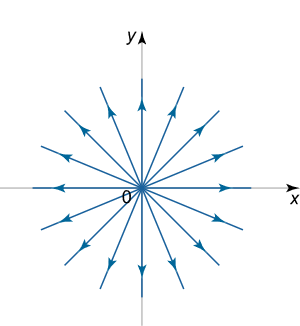
• حالت دوم: $${\lambda _1} = {\lambda _2} = {\lambda} \gt 0$$

این ترکیب از مقادیر ویژه متعلق به یک نقطه تعادل نوع گره Dicritical ناپایدار است و پرتره فاز آن مطابق با تصویر زیر است.

گره تکین

حال مجددا فرض کنید که مقادیر ویژه ماتریس A برابر با $${\lambda _1} = {\lambda _2} = {\lambda} \ne 0$$ باشند. اما در این حالت بر خلاف سیستم قبل، مرتبه فضای ویژه برابر با ۱ در نظر گرفته می‌شود. این فرض بدین معنی است که ماتریس A فقط یک مقدار ویژه $${\mathbf{V}_1}$$ دارد. بردار مستقل دوم به صورت $${\mathbf{W}_1}$$ و وابسته به $${\mathbf{V}_1}$$ تعریف می‌شود.

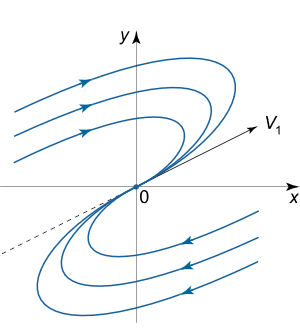
• حالت اول: $${\lambda _1} = {\lambda _2} = {\lambda} \lt 0$$

در این حالت نقطه تعادل، گره تکین پایدار نام دارد. نمایی از پرتره فاز در این سیستم به صورت شکل زیر است.

• حالت دوم: $${\lambda _1} = {\lambda _2} = {\lambda} \gt 0$$

در این حالت نقطه تعادل، گره تکین ناپایدار نام دارد. نمایی از پرتره فاز این سیستم در شکل زیر نشان داده شده است.

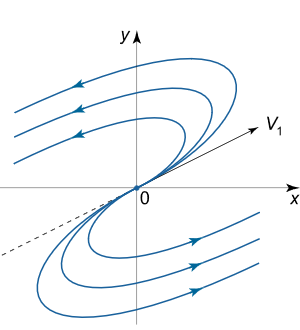
نقطه تعادل زینی

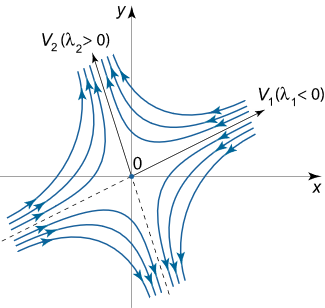
نقطه تعادل تحت شرایط زیر یک نقطه زینی محسوب می‌شود:

$${\lambda _1},{\lambda _2} \in \Re,\;\;{\lambda _1} \cdot {\lambda _2} \lt 0$$

فیلم آموزش حل تمرین طراحی کنترل غیر خطی - تابع لیاپانوف (رایگان) در فرادرس

کلیک کنید

از آن‌جا که یکی از مقادیر ویژه مثبت است، در ننتیجه نقطه زینی یک نقطه تعادل ناپایدار محسوب می‌شود. برای مثال فرض کنید $${\lambda _1} \lt 0,{\lambda _2} \gt 0$$ این مقادیر ویژه با بردارهای ویژه $${\mathbf{V}_1}$$ و $${\mathbf{V}_۲}$$ متناظر هستند. خطوط مستقیمی که در راستای بردارهای ویژه ترسیم می‌شوند، خطوط جداکننده نام دارند. این خطوط در واقع مجانب مسیرهای فاز هستند و شکل هذلولی (Hyperbola) دارند.

اگر یک مقدار ویژه منفی باشد، مثلا $${\lambda _1} \lt$$، آن‌گاه خطوط جداکننده متناظر با آن در راستای بردار ویژه $${\mathbf{V}_1}$$ خواهند بود و حرکت در طول آن به سمت نقطه تعادل $$\mathbf{X} = \mathbf{0}$$ اتفاق می‌افتد. حالت بلعکس هم به این صورت است که اگر $${\lambda _2} \gt 0$$ باشد، خطوط جداکننده در راستای بردار $${\mathbf{V}_2}$$ هستند و حرکت به سمت مبدا خواهد بود. پرتره فاز یک نقطه تعادل زینی به صورت شماتیک مانند شکل زیر است.

نقطه تعادل کانونی پایدار و ناپایدار

فرض کنید که مقادیر ویژه $$\lambda_1$$ و $$\lambda_2$$ اعداد مختلط باشند و قسمت‌های حقیقی آن‌ها غیر صفر باشند. اگر ماتریس A از اعداد حقیقی تشکیل شده باشد، ریشه‌های مختلط مانند فرم زیر اعداد مزدوج مختلط خواهند بود:

$${\lambda _{1,2}} = \alpha \pm i\beta$$

حال می‌خواهیم مسیرهای فاز را در همسایگی مبدا بیابیم. برای این هدف باید یک حل مختلط $${\mathbf{X}_1}\left( t \right)$$ متعلق به مقدار ویژه $${\lambda _1} = \alpha + i\beta$$ بیابیم.

$${{\mathbf{X}_1}\left( t \right) = {e^{{\lambda _1}t}}{\mathbf{V}_1} } = {{e^{\left( {\alpha + i\beta } \right)t}}\left( {\mathbf{U} + i\mathbf{W}} \right),}$$

اگر $${\mathbf{V}_1} = \mathbf{U} + i\mathbf{W}$$ بردار با مقدار مختلط متناظر با مقدار ویژه $${\lambda _1}$$ باشد و $$\mathbf{U}$$ و $$\mathbf{W}$$ توابع برداری حقیقی باشند، در نتیجه فرمول‌های زیر برقرار هستند:

$${{\mathbf{X}_1}\left( t \right) = {e^{\alpha t}}{e^{i\beta t}}\left( {\mathbf{U} + i\mathbf{W}} \right) } = {{e^{\alpha t}}\left( {\cos \beta t + i\sin \beta t} \right)\left( {\mathbf{U} + i\mathbf{W}} \right) } \\ = {{e^{\alpha t}}\left( {\mathbf{U}\cos \beta t + i\mathbf{U}\sin \beta t }\right.}+{\left.{ i\mathbf{W}\cos \beta t – \mathbf{W}\sin \beta t} \right) } \\ = {{e^{\alpha t}}\left( {\mathbf{U}\cos \beta t + – \mathbf{W}\sin \beta t} \right) } + {i{e^{\alpha t}}\left( {\mathbf{U}\sin \beta t + \mathbf{W}\cos \beta t} \right).}$$

در عبارت بالا، قسمت‌های حقیقی و موهومی جواب عمومی معادله را تشکیل می‌دهند.

$${\mathbf{X}\left( t \right) = {C_1}\text{Re}\left[ {{\mathbf{X}_1}\left( t \right)} \right] + {C_2}\text{Im}\left[ {{\mathbf{X}_1}\left( t \right)} \right] }\\ = {{e^{\alpha t}}\left[ {{C_1}\left( {\mathbf{U}\cos \beta t – \mathbf{W}\sin \beta t} \right)} \right. } + {\left. {{C_2}\left( {\mathbf{U}\sin \beta t + \mathbf{W}\cos \beta t} \right)} \right] } \\ = {{e^{\alpha t}}\left[ {\mathbf{U}\left( {{C_1}\cos \beta t + {C_2}\sin \beta t} \right)} \right. } + {\left. {\mathbf{W}\left( {{C_2}\cos \beta t – {C_1}\sin \beta t} \right)} \right].}$$

مقادیر ثابت‌های $$C_1$$ و $$C_2$$ را به صورت زیر بیان می‌کنیم:

$${C_1} = C\sin \delta ,\;\;{C_2} = C\cos \delta ,$$

که در این فرمول $$\delta$$ زاویه کمکی است. بنابراین جواب معادله را می‌توانیم به صورت زیر بنویسم:

$${\mathbf{X}\left( t \right) = C{e^{\alpha t}}\left[ {\mathbf{U}\left( {\sin \delta \cos \beta t + \cos \delta \sin \beta t} \right)} \right. } + {\left. {\mathbf{W}\left( {\cos\delta \cos \beta t – \sin \delta \sin \beta t} \right)} \right] } \\ = {C{e^{\alpha t}}\left[ {\mathbf{U}\sin \left( {\beta t + \delta } \right)} \right. + \left. {\mathbf{W}\cos \left( {\beta t + \delta } \right)} \right].}$$

جواب $$\mathbf{X}\left( t \right)$$ را می‌توانیم بر اساس بردارهای $$\mathbf{U}$$ و $$\mathbf{W}$$ بسط دهیم.

$$\mathbf{X}\left( t \right) = \mu \left( t \right)\mathbf{U} + \eta \left( t \right)\mathbf{W},$$

در این فرمول ضرایب $$\mu \left( t \right)$$ و $$\eta \left( t \right)$$ توسط فرمول زیر داده شده اند:

$${\mu \left( t \right) = C{e^{\alpha t}}\sin \left( {\beta t + \delta } \right),\;\;}\kern0pt {\eta \left( t \right) = C{e^{\alpha t}}\cos\left( {\beta t + \delta } \right).}$$

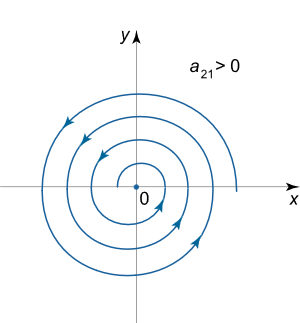
این موارد نشان می‌دهند که مسیرهای فاز به صورت مارپیچی هستند. زمانی که $$\alpha \lt 0$$ باشد، مسیرهای مارپیچی تاب خورده و به سمت مبدا نزدیک می‌شوند. چنین نقطه تعادلی را کانونی پایدار می‌نامند. به همین ترتیب اگر $$\alpha \gt 0$$ باشد، نوع نقطه تعادل کانونی ناپایدار خواهد بود.

جهت مسیرها را می‌توان با استفاده از علامت $${a_{21}}$$ در ماتریس اصلی A تعیین کرد. به عنوان مثال، مشتق $${\large\frac{{dy}}{{dt}}\normalsize}$$ را در نقطه $$(0,1)$$ به صورت زیر در نظر بگیرید:

$$\frac{{dy}}{{dt}}\left( {1,0} \right) = {a_{21}} \cdot 1 + {a_{22}} \cdot 0 = {a_{21}}$$

ضریب مثبت $${a_{21}} \gt 0$$، متناظر با مسیری است که در خلاف جهت حرکت عقربه ساعت پیچ می‌خورد و در شکل زیر نمایی از چنین پرتره فازی نشان داده شده است.

اما زمانی که $${a_{21}} \lt 0$$ باشد، مسیرهای فاز در جهت حرکت عقربه‌های ساعت پیچ می‌خورند. پرتره فاز در این حالت را در شکل زیر می‌توان دید.

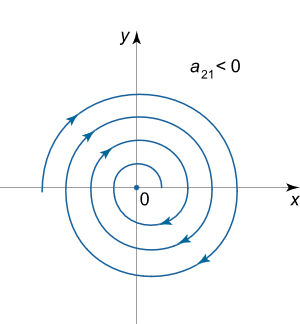
بنابراین با احتساب جهت‌های مسیر فاز، می‌توان گفت که ۴ نوع مختلف نقطه تعادل کانونی وجود دارد. یعنی علاوه بر دو نوعی که در شکل‌های بالا معرفی شد، دو نوع دیگر نیز امکان‌پذیر است که شماتیکی از آن‌ها را در شکل‌های زیر می‌توانیم ببینیم.

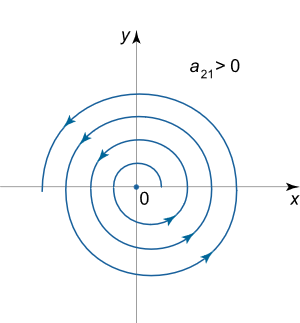
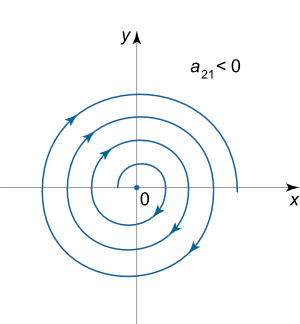
نقطه تعادل مرکزی

اگر مقادیر ویژه ماتریس A اعدادی کاملا موهومی باشند، آن‌گاه نقاط تعادل سیستم را نوع مرکزی می‌نامند. برای یک ماتریس با المان‌های حقیقی، مقادیر ویژه موهومی، جفت اعداد مختلط مزدوج هستند. در مورد نقاط تعادل نوع مرکزی، مسیرهای فاز معمولا از معادله مسیرها در $$\alpha = 0$$ به دست می‌آیند و بیضی شکل هستند. به عبارت دیگر می‌توان گفت که این مسیرها حرکت تناوبی یک نقطه در فضای فاز را نشان می‌دهند. یک نقطه تعادل نوع مرکزی، طبق معیار پایداری لیاپانوف، پایدار محسوب می‌شود.

فیلم آموزش ارتعاشات غیر خطی – جامع و با نکات مهم در فرادرس

کلیک کنید

دو نوع نقطه تعادل مرکزی وجود دارند که از لحاظ جهت حرکت مسیرها متفاوت هستند. شکل‌های زیر انواع این نقاط تعادل را نشان می‌دهند.

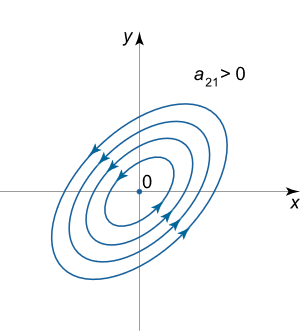
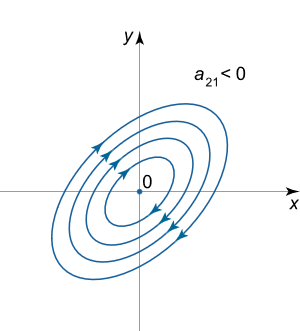
همانند نقطه تعادل نوع کانونی، جهت‌های حرکت را می‌توان از روی علامت مشتق $$\large\frac{{dy}}{{dt}}\normalsize$$ در نقاط مختلف تعیین کرد. به عنوان مثال اگر نقطه $$\left( {1,0} \right)$$ را در نظر بگیریم، آن‌گاه داریم:

$$\frac{{dy}}{{dt}}\left( {1,0} \right) = {a_{21}}$$

به همین دلیل است که جهت چرخش را با استفاده از علامت ضریب $${a_{21}}$$ تعیین می‌کنند.

بنابراین،‌ تا این قسمت انواع مختلف نقاط پایداری را به شرط این که ماتریس A یک ماتریس ناتکین باشد، در نظر گرفته‌ایم $$\left( {\det A \ne 0} \right)$$. با احتساب جهت‌های مسیرهای فاز، می‌توان گفت که در مجموع ۱۳ پرتره فاز مختلف وجود دارد که در شکل‌های بالا به تمام آن‌ها اشاره شده است.

حال می‌خواهیم به بررسی پرتره فاز در موردی که ماتریس A تکین باشد، بپردازیم.

ماتریس تکین

اگر ماتریس A تکین باشد، آن‌گاه یک و یا هر دو مقدار ویژه برابر با صفر هستند. در این حالت، موارد زیر امکان دارد به وقوع بپیوندند:

• حالت اول: $${\lambda _1} \ne 0,\; {\lambda _2} = 0$$

در این حالت، حل عمومی فرم زیر را خواهد داشت:

$$\mathbf{X}\left( t \right) = {C_1}{e^{{\lambda _1}t}}{\mathbf{V}_1} + {C_2}{\mathbf{V}_2}$$

که در این معادله $${\mathbf{V}_2} = {\left( {{V_{12}},{V_{22}}} \right)^T}$$ و $${\mathbf{V}_2} = {\left( {{V_{12}},{V_{22}}} \right)^T}$$ بردارهای ویژه متناظر با مقادیر ویژه $${\lambda _1}$$ و $${\lambda _2}$$ هستند. در این حالت تمام خطوط از مبدا می‌گذرند و در راستای بردار ویژه $${\mathbf{V}_2}$$ هستند. نقاط تعادل در این حالت نام خاصی ندارند و بر روی بردار ویژه $${\mathbf{V}_2}$$ قرار دارند. مسیرهای فاز با بردار ویژه دیگر یعنی $${\mathbf{V}_1}$$ موازی هستند. بسته به علامت $${\lambda _1}$$، حرکت در زمان $$t \to \infty$$ یا در جهت نزدیک‌شونده به بردار $${\mathbf{V}_2}$$ و یا در جهت دورشونده از آن است. این دو حالت در تصاویر زیر نشان داده شده‌اند.

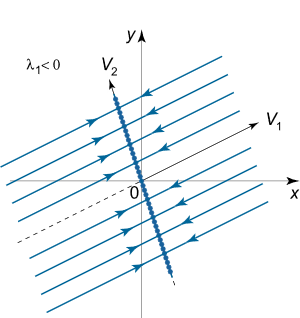
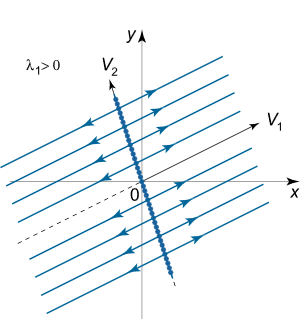
• حالت دوم: $${\lambda _1} = {\lambda _2} = 0,\; \dim \ker A = 2$$

در این حالت، ابعاد فضای ویژه ماتریس برابر با ۲ است و بنابراین دو بردار ویژه $${\mathbf{V}_1}$$ و $${\mathbf{V}_2}$$ وجود دارند. این اتفاق ممکن است زمانی پیش بیاید که ماتریس A یک ماتریس صفر باشد. حل عمومی به صورت زیر خواهد بود:

$$\mathbf{X}\left( t \right) = {C_1}{\mathbf{V}_1} + {C_2}{\mathbf{V}_2}$$

در این حالت، هر نقطه در سیستم یک نقطه تعادل سیستم محسوب می‌شود.

• حالت سوم: $${\lambda _1} = {\lambda _2} = 0,\; \dim \ker A = 1$$

این حالت به این جهت از حالت قبلی متفاوت است که فقط یک بردار ویژه دارد. بنابراین ماتریس A ماتریسی غیر صفر است. می‌توان بردار ویژه $${\mathbf{W}_1}$$ را به عنوان یک بردار مستقل مرتبه دوم در نظر گرفت که با بردار $${\mathbf{V}_1}$$ مرتبط است. جواب عمومی را می‌توان به صورت زیر در نظر گرفت:

$$\mathbf{X}\left( t \right) = \left( {{C_1} + {C_2}t} \right){\mathbf{V}_1} + {C_2}{\mathbf{W}_1}$$

در این حالت، تمام نقاط بر روی خطی قرار دارند که این خط از مبدا می‌گذرد. همچنین این خط در راستای بردار ویژه $${\mathbf{V}_1}$$ قرار گرفته است. نقاط در این حالت ناپایدار هستند. مسیرهای فاز به صورت خطوطی مستقیم و موازی با بردار ویژه $${\mathbf{V}_1}$$ ترسیم می‌شوند. جهت حرکت این خط‌ها در زمان $$t \to \infty$$ به ضریب ثابت $${C_2}$$ بستگی دارند. اگر این ضریب منفی باشد ($${C_2} \lt 0$$) جهت حرکت از چپ به راست خواهد بود. اما اگر ضریب مقدار مثبت داشته باشد ($${C_2} \gt 0$$)، آن‌گاه جهت حرکت برعکس و از راست به چپ خواهد بود. تصویر زیر پرتره فاز را در این حالت نشان می‌دهد.

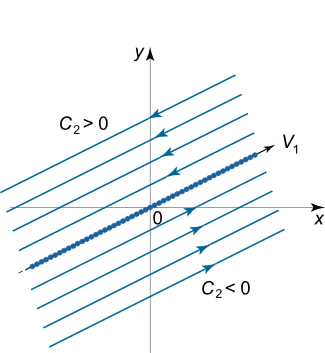
دیاگرام دوشاخگی

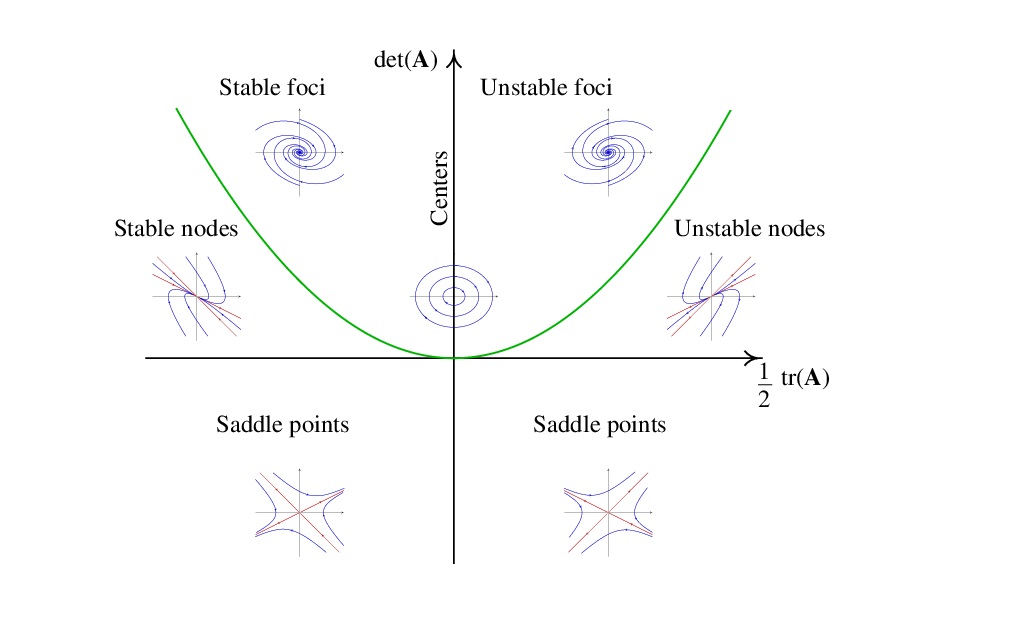
در مطالب بالا به بررسی و طبقه‌بندی انواع مختلف نقاط پایداری در سیستم‌های خطی بر اساس مقادیر ویژه پرداختیم. البته امکان تشخیص نوع نقطه پایداری بدون استفاده از مقادیر ویژه $${\lambda _1}$$ و $${\lambda _2}$$ هم وجود دارد و در این روش صرفا بر اساس دانستن دترمینان ماتریس A و نیز مقدار اثر (Trace) ماتریس یا $$\text{tr}\,A$$ می‌توانیم نوع نقطه پایداری را تعیین می‌کنیم.

$${A = \left( {\begin{array}{*{20}{c}}<br /> {{a_{11}}}&{{a_{12}}}\\<br /> {{a_{21}}}&{{a_{22}}}<br /> \end{array}} \right),}\;\;<br /> {\text{tr}\,A = {a_{11}} + {a_{22}},}\;\;<br /> {\det A = {a_{11}}{a_{22}} – {a_{12}}{a_{21}}.} $$

فیلم آموزش کنترل صنعتی – حل مساله در فرادرس

کلیک کنید

معادله کمکی ماتریس به صورت زیر است:

$${\lambda ^2} – \left( {{a_{11}} + {a_{22}}} \right)\lambda + {a_{11}}{a_{22}} – {a_{12}}{a_{21}} = 0.$$

معادله بالا را می‌توان بر حسب دترمینان ماتریس و نیز اثر ماتریس بازنویسی کرد:

$${\lambda ^2} – \text{tr}\,A \cdot \lambda + \det A = 0.$$

مبین یا $$\triangle$$ این معادله درجه دوم به صورت زیر است:

$$D = {\left( {\text{tr}\,A} \right)^2} – 4\det A.$$

بنابراین منحنی دو شاخگی (Bifurcation) این معادله را می‌توان در فضای $$\left( {\text{tr}\,A,\det A} \right)$$ مانند شکل زیر ترسیم کرد تا نواحی مختلف پایداری سیستم تعیین شوند.

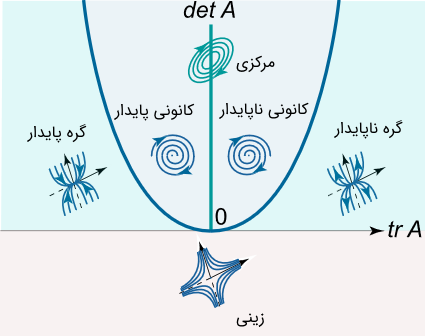
بر اساس فرمول زیر، این منحنی دارای شکل بیضی است.

$$\det A = {\left( {\frac{\text{tr}\,A}{2}} \right)^2}$$

نقاط تعادل نوع کانونی و مرکزی در بالای بیضی قرار دارند. نقاط نوع مرکزی به شرط این‌که $$\text{tr}\,A = 0$$ باشد، در قسمت مثبت محور Y قرار می‌گیرند. اما نقاط تعادل زینی و نیز گره در قسمت پایین بیضی هستند. خود بیضی هم شامل نقاط تعادل گره تکین و گره Dicritical است.

به صورت کلی می‌توان گفت که مودهای پایدار حرکتی در ربع بالا سمت چپ نمودار دوشاخگی قرار گرفته‌اند و سه ربع دیگر این نمودار متناظر با نقاط تعادل ناپایدار هستند.

نحوه ترسیم پرتره فاز

برای ترسیم پرتره فاز سیستم خطی مستقل درجه دوم با ضرایب ثابت به صورت زیر:

$${\mathbf{X’} = A\mathbf{X},}\;\;<br /> {A = \left[ {\begin{array}{*{20}{c}}<br /> {{a_{11}}}&{{a_{12}}}\\<br /> {{a_{21}}}&{{a_{22}}}<br /> \end{array}} \right],\;\;}\kern0pt<br /> {\mathbf{X} = \left[ {\begin{array}{*{20}{c}}<br /> x\\<br /> y<br /> \end{array}} \right],} $$

انجام مراحل زیر ضروری است.

• گام اول: مقادیر کمکی را با حل کردن معادله کمکی زیر به دست آورد:

$${\lambda ^2} – \left( {{a_{11}} + {a_{22}}} \right)\lambda + {a_{11}}{a_{22}} – {a_{12}}{a_{21}} = 0.$$

• گام دوم: نوع نقطه تعادل و مولفه پایداری آن را مشخص کرد. نوع نقطه پایداری را می‌توان بر اساس منحنی دوشاخگی که در بخش قبل به آن پرداختیم، نیز تعیین کرد. برای این کار، دانستن دترمینان و اثر ماتریس A لازم است.

$${\text{tr}\,A = {a_{11}} + {a_{22}},}\;\;<br /> {\det A = \left| {\begin{array}{*{20}{c}}<br /> {{a_{11}}}&{{a_{12}}}\\<br /> {{a_{21}}}&{{a_{22}}}<br /> \end{array}} \right| }<br /> = {{a_{11}}{a_{22}} – {a_{12}}{a_{21}}.}$$

• گام سوم: در این مرحله باید معادله خطوط هم‌شیب یا ایزوکلاین‌ها (Isoclines) را به دست آورد.

$${\frac{{dx}}{{dt}} = {a_{11}}x + {a_{12}}y}\;\; {\left( \text{vertical isocline} \right),}$$

$${\frac{{dy}}{{dt}} = {a_{21}}x + {a_{22}}y}\;\; {\left( \text{horizontal isocline} \right).}$$

• گام چهارم: اگر نوع نقطه تعادل گره و یا زینی باشد، آن‌گاه لازم است تا بردارهای ویژه را نیز محاسبه کرد و مجانب‌ها را موازی با بردارهای ویژه و گذرا از مبدا ترسیم کرد.
• گام پنجم: در این مرحله باید پرتره فاز را به صورت شماتیکی ترسیم کرد.
• گام ششم: بسته به پایداری و یا ناپایداری نقطه تعادل، جهت حرکت روی مسیرهای فاز را مشخص کرده و اگر نوع نقطه تعادل کانونی باشد، باید جهت چرخش مسیرهای فاز را مشخص کرد. این کار با محاسبه بردار سرعت $$\left( {{\large\frac{{dx}}{{dt}}\normalsize}, {\large\frac{{dy}}{{dt}}\normalsize}} \right)$$ در نقاط مختلف مانند $$\left( {1,0} \right)$$ امکان‌‌پذیر است.

به طریق مشابه، اگر نوع نقطه تعادل مرکزی باشد هم جهت حرکت را تعیین می‌کنیم.

البته به این نکته توجه شود که الگوریتم توضیح داده شده در این قسمت، یک روش قطعی برای ترسیم پرتره فاز نبوده و در مسائل خاص تکنیک‌های مختلفی به منظور تسهیل در ترسیم مورد استفاده قرار می‌گیرد.

مثال ۱:

نقاط تعادل سیستم خطی مستقل درجه دوم زیر را به دست آورید و پرتره فاز سیستم را ترسیم کنید.

$$\frac{{dx}}{{dt}} = – x,\;\;\frac{{dy}}{{dt}} = 2x – 2y.$$

حل:

ابتدا ماتریس A این سیستم را نوشته و مقدار دترمینان آن را به دست می‌آوریم.

$${A = \left[ {\begin{array}{*{20}{r}}<br /> { – 1}&0\\<br /> 2&{ – 2}<br /> \end{array}} \right],\;\;}\kern0pt<br /> {\det A = \left| {\begin{array}{*{20}{r}}<br /> { – 1}&0\\<br /> 2&{ – 2}<br /> \end{array}} \right| = 2 \ne 0.} $$

چون دترمینان ماتریس صفر نیست، در نتیجه معادله $$\mathbf{X} = \mathbf{0}$$ دارای نقاط تعادل یکتا خواهد بود. مقادیر ویژه ماتریس A را می‌توانیم به صورت زیر به دست بیاوریم:

$${\det \left( {A – \lambda I} \right) = 0,\;\;}\Rightarrow<br /> {\left| {\begin{array}{*{20}{c}}<br /> { – 1 – \lambda }&0\\<br /> 2&{ – 2 – \lambda }<br /> \end{array}} \right| = 0,\;\;}\Rightarrow<br /> {\left( {\lambda + 1} \right)\left( {\lambda + 2} \right) = 0,\;\;}\Rightarrow<br /> {{\lambda _1} = – 1,\;{\lambda _2} = – 2.} $$

هر دو مقدار ویژه حقیقی و منفی هستند، در نتیجه نقطه تعادل از نوع گره پایدار است. حال معادله ایزوکلاین‌ها یا به عبارت دیگر خطوطی که بر مسیرهای فاز مماس هستند، را به دست می‌آوریم. ایزوکلاین‌های عمودی به صورت زیر هستند:

$$\frac{{dx}}{{dt}} = – x = 0\;\;\text{or}\;\;x = 0.$$

معادله ایزوکلاین‌های افقی را نیز می‌توان به صورت زیر به دست آورد:

$$\frac{{dy}}{{dt}} = 2x – 2y = 0\;\;\text{or}\;\;y = x.$$

حال باید معادله مجانب‌ها را به دست بیاوریم. این کار توسط محاسبه بردارهای ویژه $${\mathbf{V}_1}$$ و $${\mathbf{V}_۲}$$ ماتریس A انجام می‌شود.

$${\left( {A – {\lambda _1}I} \right){\mathbf{V}_1} = \mathbf{0},\;\;}\Rightarrow<br /> {\left[ {\begin{array}{*{20}{c}}<br /> { – 1 + 1}&0\\<br /> 2&{ – 2 + 1}<br /> \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> {{V_{11}}}\\<br /> {{V_{21}}}<br /> \end{array}} \right] = \mathbf{0},\;\;}\Rightarrow \\<br /> {\left[ {\begin{array}{*{20}{r}}<br /> 0&0\\<br /> 2&{ – 1}<br /> \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> {{V_{11}}}\\<br /> {{V_{21}}}<br /> \end{array}} \right] = \mathbf{0},\;\;}\Rightarrow<br /> {2{V_{11}} – {V_{21}} = 0,\;\;}\Rightarrow<br /> {{V_{11}} = 1,\;{V_{21}} = 2,\;\;}\Rightarrow\\<br /> {{\mathbf{V}_1} = \left[ {\begin{array}{*{20}{c}}<br /> {{V_{11}}}\\<br /> {{V_{21}}}<br /> \end{array}} \right] = \left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> 2<br /> \end{array}} \right];} $$

بردار ویژه $${\mathbf{V}_2}$$ نیز به صورت زیر است:

$${\left( {A – {\lambda _2}I} \right){\mathbf{V}_2} = \mathbf{0},\;\;}\Rightarrow<br /> {\left[ {\begin{array}{*{20}{c}}<br /> { – 1 + 2}&0\\<br /> 2&{ – 2 + 2}<br /> \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> {{V_{12}}}\\<br /> {{V_{22}}}<br /> \end{array}} \right] = \mathbf{0},\;\;}\Rightarrow \\<br /> {\left[ {\begin{array}{*{20}{c}}<br /> 1&0\\<br /> 2&0<br /> \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> {{V_{12}}}\\<br /> {{V_{22}}}<br /> \end{array}} \right] = \mathbf{0},\;\;}\Rightarrow<br /> {\left\{ {\begin{array}{*{20}{l}}<br /> {1 \cdot {V_{12}} + 0 \cdot {V_{22}} = 0}\\<br /> {2 \cdot {V_{12}} + 0 \cdot {V_{22}} = 0}<br /> \end{array}} \right.,\;\;}\Rightarrow<br /> {{V_{12}} = 0,\;{V_{22}} = 1,\;\;}\Rightarrow \\<br /> {{\mathbf{V}_2} = \left[ {\begin{array}{*{20}{c}}<br /> {{V_{12}}}\\<br /> {{V_{22}}}<br /> \end{array}} \right] = \left[ {\begin{array}{*{20}{c}}<br /> 0\\<br /> 1<br /> \end{array}} \right].} $$

حال در صفحه مختصات X-Y، بردارهای ویژه و ایزوکلاین $$y = x$$ را ترسیم می‌کنیم و پرتره فاز را مانند تصویر زیر ترسیم می‌کنیم.

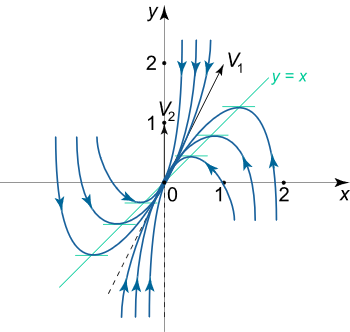
همان‌ طور که از روی تصویر نیز مشخص است، مسیرهای فاز به صفر نزدیک می‌شوند و خط در راستای بردار ویژه $${\mathbf{V}_1}$$ را لمس می‌کنند؛ زیرا این خط متناظر با کوچک‌ترین مقدار ویژه (در این‌جا $$\left| {{\lambda _1}} \right| = 1$$) است.

مثال ۲:

نقاط تعادل سیستم زیر را تعیین کنید و پرتره فاز آن را نیز رسم کنید.

$$\frac{{dx}}{{dt}} = x + 3y,\;\;\frac{{dy}}{{dt}} = 2x.$$

حل:

ابتدا باید از صفر نبودن دترمینان ماتریس A اطمینان حاصل شود.

$${A = \left( {\begin{array}{*{20}{c}}<br /> 1&3\\<br /> 2&0<br /> \end{array}} \right),\;\;}\kern0pt<br /> {\det A = \left| {\begin{array}{*{20}{c}}<br /> 1&3\\<br /> 2&0<br /> \end{array}} \right| = – 6 \ne 0.} $$

در این حالت سیستم دارای یک نقطه تعادل است. این مسئله را می‌توانیم بدون محاسبه مقادیر ویژه و بردارهای ویژه نیز حل کنیم. چون مقدار دترمینان عددی منفی است، در نتیجه نقطه پایداری صفر از نوع زینی محسوب می‌شود که این را می‌توان با استفاده از نمودار دوشاخگی بالا تشخیص داد.

در گام بعد باید معادله ایزوکلاین‌ها را تعیین کنیم. تابع خطی زیر، معادله ایزوکلاین عمودی را مشخص می‌کند:

$$\frac{{dx}}{{dt}} = x + 3y = 0,\;\; \Rightarrow y = – \frac{x}{3}.$$

معادله ایزوکلاین‌های افقی به صورت زیر است:

$$\frac{{dy}}{{dt}} = 2x = 0,\;\; \Rightarrow x = 0\;\left( {y-\text{axis}} \right).$$

معادله خطوط جداکننده دارای فرم $$y = kx$$ است. با جایگذاری این مقدار در معادله سیستم اصلی، به یک معادله درجه دو برای ضریب K دست می‌یابیم.

$${\left\{ \begin{array}{l} \frac{{dx}}{{dt}} = x + 3y \\ \frac{{dy}}{{dt}} = 2x \end{array} \right.,\;\;}\Rightarrow {\left\{ \begin{array}{l} \frac{{dx}}{{dt}} = x + 3kx \\ \frac{{kdx}}{{dt}} = 2x \end{array} \right.,\;\;}\Rightarrow {2x = k\left( {x + 3kx} \right),\;\;}\Rightarrow \\ {3{k^2}x + kx – 2x = 0,\;\;}\Rightarrow {3{k^2} + k – 2 = 0,\;\;}\Rightarrow \\ {D = 24,\;{k_{1,2}} = \frac{{ – 1 \pm 5}}{6} = – 1,\;\frac{2}{3}.}$$

بنابراین معادله خطوط جداکننده به صورت زیر به دست می‌آیند:

$$y = – x,\;\;y = \frac{2}{3}x.$$

حال نوبت به این می‌رسد که خطوط جداکننده و نیز ایزوکلاین‌ها و سپس مسیرهای فاز را در صفحه فاز ترسیم کنیم. همچنین باید جهت حرکت بر روی مسیرهای فاز را هم مشخص کنیم. نقطه $$\left( {1,0} \right)$$ را به عنوان مثال در نظر بگیرید و مقدار $$\large\frac{{dy}}{{dt}}\normalsize$$ را در آن محاسبه کنید:

$$\frac{{dy}}{{dt}}\left( {1,0} \right) = 2 \cdot 1 = 2 > 0.$$

چون مقدار مشتق در این نقطه مثبت است، در نتیجه با افزایش زمان t، این نقطه در جهتی به سمت بالا از محور X عبور می‌کند. با استفاده از خاصیت وجود تقارن در این نمودار، به سادگی می‌توانیم جهت حرکت را برای سایر مسیرهای فاز ترسیم کنیم.

در نهایت پرتره فاز به صورت شکل زیر خواهد بود.

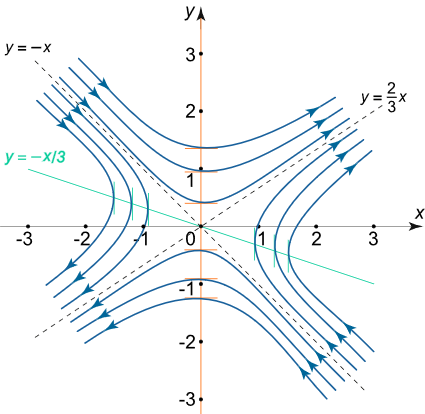
مثال ۳:

نوع نقاط تعادل را در سیستم زیر مشخص کنید و سپس پرتره فاز را ترسیم کنید.

$$\frac{{dx}}{{dt}} = 3x – 4y,\;\;\frac{{dy}}{{dt}} = 2x – y$$

حل:

دترمینان سیستم به صورت زیر است:

$${A = \left[ {\begin{array}{*{20}{c}}<br /> 3&{ – 4}\\<br /> 2&{ – 1}<br /> \end{array}} \right],\;\;}\kern0pt<br /> {\det A = \left| {\begin{array}{*{20}{c}}<br /> 3&{ – 4}\\<br /> 2&{ – 1}<br /> \end{array}} \right| = 5 \ne 0.} $$

در این حالت سیستم دارای یک نقطه تعادل یکتا در $$\left( {0,0} \right)$$ خواهد بود. برای محاسبه مقادیر ویژه ماتریس A به صورت زیر عمل می‌کنیم:

$${\left| {\begin{array}{*{20}{c}}<br /> {3 – \lambda }&{ – 4}\\<br /> 2&{ – 1 – \lambda }<br /> \end{array}} \right| = 0,\;\;}\Rightarrow<br /> {\left( {\lambda – 3} \right)\left( {\lambda + 1} \right) + 8 = 0,\;\;}\Rightarrow \\<br /> {{\lambda ^2} – 2\lambda + 5 = 0,\;D = – 16,\;\;}\Rightarrow<br /> {{\lambda _{1,2}} = \frac{{2 \pm 4i}}{2} = 1 \pm 2i.} $$

مقادیر ویژه $${\lambda_1}$$ و $${\lambda_2}$$ اعداد مختلط مزدوج هستند که در آن‌ها قسمت حقیقی مثبت است. بنابراین، موقعیت نقطه تعادل در مبدا به صورت کانونی ناپایدار خواهد بود.

حال باید معادلات مربوط به ایزوکلاین‌ها را به دست بیاوریم. معادله ایزوکلاین عمودی به صورت زیر به دست می‌آید:

$$\frac{{dx}}{{dt}} = 3x – 4y = 0,\;\; \Rightarrow y = \frac{3}{4}x.$$

معادله ایزوکلاین افقی نیز به صورت زیر است:

$$\frac{{dy}}{{dt}} = 2x – y = 0,\;\; \Rightarrow y = 2x.$$

برای پی بردن به جهت چرخش در مسیرهای فاز باید مقدار مشتق $$\large\frac{{dy}}{{dt}}\normalsize$$ را در نقطه $$\left( {1,0} \right)$$ به دست بیاوریم.

$$\frac{{dy}}{{dt}}\left( {1,0} \right) = 2 \cdot 1 – 0 = 2 \gt 0.$$

بنابراین، جهت چرخش مسیرهای فاز در خلاف جهت حرکت عقربه‌های ساعت است.

حال بر اساس اطلاعاتی که تا این قسمت به دست آمده است، می‌توانیم پرتره فاز را مانند شکل زیر ترسیم کنیم.

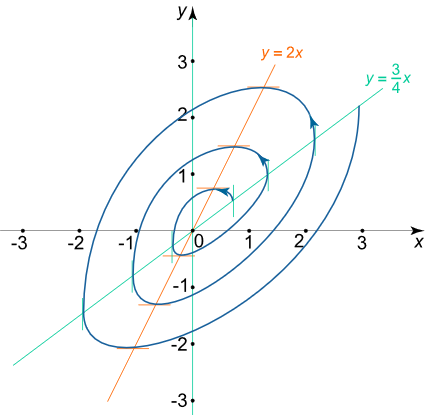
مثال ۴:

پایداری سیستم زیر را بر حسب مقدار پارامتر $$a$$ مورد بررسی قرار دهید.

$$\frac{{dx}}{{dt}} = ax + y,\;\;\frac{{dy}}{{dt}} = x + ay.$$

فیلم آموزش مدل های غیرخطی و پدیده های غیرخطی (رایگان) در فرادرس

کلیک کنید

حل: 

مقدار دترمینان و اثر ماتریس A را محاسبه می‌کنیم:

$${A = \left[ {\begin{array}{*{20}{c}}<br /> a&1\\<br /> 1&a<br /> \end{array}} \right],\;\;}\kern0pt<br /> {\text{tr}\,A = 2a,\;\;}\kern0pt<br /> {\det A = {a^2} – 1.} $$

معادله کمکی سیستم را می‌توان به صورت زیر نوشت:

$${{\lambda ^2} – \text{tr}\,A \cdot \lambda + \det A = 0,\;\;}\Rightarrow {{\lambda ^2} – 2a\lambda + {a^2} – 1 = 0.}$$

مقدار $$\triangle$$ این معادله درجه دوم را به دست می‌آوریم:

$$\require{cancel}<br /> {D = {\left( { – 2a} \right)^2} – 4\left( {{a^2} – 1} \right) }<br /> = {\cancel{4{a^2}} – \cancel{4{a^2}} + 4 = 4 \gt 0.} $$

چون مقدار مبین این معادله در همه جا مثبت است، بنابراین مقادیر ویژه به ازای تمام مقادیر $$a$$ حقیقی خواهد بود. این بدین معنی است که اگر دترمینان ماتریس A غیر صفر باشد، سیستم دارای یک نقطه تعادل یکتا در مبدا خواهد بود. این نقطه تعادل یا از نوع زینی و یا گره است.

حال باید مشخص کنیم که این نقطه تعادل به ازای چه مقادیری از $$a$$ نوع زینی است. بر اساس دیاگرام دوشاخگی، نقطه زینی زمانی وجود دارد که $$\det A \lt 0$$ باشد. در نتیجه نامساوی زیر برقرار است:

$${\det A = {a^2} – 1 \lt 0,\;\;} \Rightarrow {a \in \left( { – 1,1} \right).}$$

بنابراین به ازای $$a \in \left( { – 1,1} \right)$$ در مبدا یک نقطه تعادل زینی وجود دارد.

واضح است که نقطه تعادل به ازای مقادیر زیر از نوع گره است.

$$a \in \left( { – \infty , – 1} \right) \cup \left( {1,\infty } \right).$$

به علاوه، اگر $$\text{tr}\,A = 2a \gt 0$$ یا $$a \gt 0$$ باشد، آن‌گاه نقطه تعادل گره ناپایدار خواهد بود. همچنین اگر $$\text{tr}\,A = 2a \lt 0$$ یا $$a \lt 0$$ باشد، یک نقطه تعادل نوع گره پایدار در سیستم وجود دارد. در نتیجه عبارات زیر برقرار خواهند بود:

$$a \in \left( {-\infty,-1 } \right) – \text{stable node},$$

$$a \in \left( {1,\infty } \right) – \text{unstable node}.$$

توجه کنید که به ازای هیچ کدام از مقادیر $$a$$، نقطه تعادل بر نمودار بیضی روی دیاگرام دوشاخگی قرار نمی‌گیرد. در واقع، معادله این بیضی به صورت زیر است:

$$\det A = {\left( {\frac{\text{tr}\,A}{2}} \right)^2}.$$

با جایگذاری مقادیر این مثال در معادله بالا، به عبارت زیر می‌رسیم:

$${{a^2} – 1 = {\left( {\frac{{2a}}{2}} \right)^2},\;\;}\Rightarrow {{a^2} – 1 = {a^2},\;\;}\Rightarrow { – 1 = 0,}$$

مشاهده می‌کنید که این معادله صحیح نیست.

موارد روی نقاط مرزی $$a = \pm 1$$ را به صورت جداگانه بررسی می‌کنیم. به ازای این مقادیر $$a$$، سیستم تکین است.

$$\det A = {a^2} – 1 = 0.$$

فرض کنید که $$a = 1$$ باشد. مقادیر ویژه را به صورت زیر محاسبه می‌کنیم:

$${A = \left[ {\begin{array}{*{20}{c}}<br /> 1&1\\<br /> 1&1<br /> \end{array}} \right],\;\;}\kern0pt<br /> {\det \left( {A – \lambda I} \right) = 0,\;\;}\Rightarrow<br /> {\left| {\begin{array}{*{20}{c}}<br /> {1 – \lambda }&1\\<br /> 1&{1 – \lambda }<br /> \end{array}} \right| = 0,\;\;}\Rightarrow\\<br /> {{\left( {\lambda – 1} \right)^2} – 1 = 0,\;\;}\Rightarrow<br /> {\left| {\lambda – 1} \right| = 1,\;\;}\Rightarrow<br /> {{\lambda _{1,2}} = 1 \pm 1 = 0,\;2.}$$

بردار ویژه $${\mathbf{V}_1}$$ متناظر با مقدار ویژه $${\lambda_1} = 0$$ را محاسبه می‌کنیم.

$${\left[ {\begin{array}{*{20}{c}}<br /> {1 – 0}&1\\<br /> 1&{1 – 0}<br /> \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> {{V_{11}}}\\<br /> {{V_{21}}}<br /> \end{array}} \right] = \mathbf{0},\;\;}\Rightarrow<br /> {\left[ {\begin{array}{*{20}{c}}<br /> 1&1\\<br /> 1&1<br /> \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> {{V_{11}}}\\<br /> {{V_{21}}}<br /> \end{array}} \right] = \mathbf{0},\;\;}\Rightarrow\\<br /> {{V_{11}} + {V_{21}} = 0,\;\;}\Rightarrow<br /> {{V_{21}} = 1,\;{V_{11}} = – 1,\;\;}\Rightarrow<br /> {{\mathbf{V}_1} = \left[ {\begin{array}{*{20}{r}}<br /> { – 1}\\<br /> 1<br /> \end{array}} \right].}$$

خطی راست موازی با بردار $${\mathbf{V}_1}$$ که از مبدا هم می‌گذرد، دارای معادله $$y = -x$$ است. هر نقطه بر روی این خط، یک نقطه تعادل برای این سیستم محسوب می‌شود و تمام این نقاط تعادل ناپایدار هم هستند؛ زیرا مقدار ویژه دوم مثبت است ($${\lambda_2} = 2 \gt 0.$$).

حال فرض کنید که $$a = -1$$ باشد. به طریق مشابه می‌توانیم مقدار ویژه را به ازای این $$a$$ نیز به دست آوریم.

$${A = \left[ {\begin{array}{*{20}{r}}<br /> { – 1}&1\\<br /> 1&{ – 1}<br /> \end{array}} \right],\;\;}\kern0pt<br /> {\det \left( {A – \lambda I} \right) = 0,\;\;}\Rightarrow<br /> {\left| {\begin{array}{*{20}{c}}<br /> { – 1 – \lambda }&1\\<br /> 1&{ – 1 – \lambda }<br /> \end{array}} \right| = 0,\;\;}\Rightarrow \\<br /> {{\left( {\lambda + 1} \right)^2} – 1 = 0,\;\;}\Rightarrow<br /> {\left| {\lambda + 1} \right| = 1,\;\;}\Rightarrow<br /> {{\lambda _{1,2}} = – 1 \pm 1 = 0,\; – 2.} $$

حال باید بردار ویژه $${\mathbf{U}_1} = {\left( {{U_{11}},{U_{21}}} \right)^T}$$ متناظر با مقدار ویژه $${\lambda_1} = 0$$ را محاسبه کنیم.

$${\left[ {\begin{array}{*{20}{c}}<br /> { – 1 – 0}&1\\<br /> 1&{ – 1 – 0}<br /> \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> {{U_{11}}}\\<br /> {{U_{21}}}<br /> \end{array}} \right] = \mathbf{0},\;\;}\Rightarrow<br /> {\left[ {\begin{array}{*{20}{r}}<br /> { – 1}&1\\<br /> 1&{ – 1}<br /> \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> {{U_{11}}}\\<br /> {{U_{21}}}<br /> \end{array}} \right] = \mathbf{0},\;\;}\Rightarrow \\<br /> { – {U_{11}} + {U_{21}} = 0,\;\;}\Rightarrow<br /> {{U_{21}} = 1,\;{U_{11}} = 1,\;\;}\Rightarrow<br /> {{\mathbf{U}_1} = \left[ {\begin{array}{*{20}{c}}<br /> {{U_{11}}}\\<br /> {{U_{21}}}<br /> \end{array}} \right] = \left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> 1<br /> \end{array}} \right].} $$

این بردار متناظر با خط راست $$y = x$$ است که از مبدا می‌گذرد. تمام نقاط روی این خط، نقاط تعادل هستند. این نقاط تعادل پایدار هستند؛ زیرا $${\lambda_2} = -2 \lt 0$$.

حال با ترکیب کردن تمام این حالت‌ها، نتایج نهایی را می‌توانیم به صورت زیر بنویسیم. سیستم به ازای مقادیر مختلف برای پارامتر $$a$$، دارای نقاط تعادل زیر است.

• زمانی که $$a \in \left( { – \infty , – 1} \right),$$ باشد، یک گره پایدار در مبدا وجود دارد.
• زمانی که $$a = -1$$ باشد، هر نقطه بر روی خط $$a = -1$$ یک نقطه تعادل پایدار است.
• زمانی که $$a \in \left( { – 1, 1} \right),$$ باشد، یک نقطه زینی در مبدا وجود دارد.
• زمانی که $$a = 1$$ باشد، آن‌گاه هر نقطه روی خط $$y = -x$$ نقطه تعادل ناپایدار است.
• زمانی که $$a \in \left( {1, \infty} \right)$$ باشد، یک گره ناپایدار در مبدا مختصات وجود دارد.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های مهندسی کنترل
• آموزش طراحی سیستم های کنترل غیر خطی
• مجموعه آموزش ریاضیات
• آموزش جبر خطی با متلب
• سیستم غیر خطی — راهنمای جامع
• خطی سازی سیستم های غیر خطی — از صفر تا صد
• تابع لیاپانوف (Lyapunov Function) — از صفر تا صد

^^