تابع لیاپانوف (Lyapunov Function) – از صفر تا صد (+ دانلود فیلم آموزش رایگان)

در راستای ارائه مفاهیم مرتبط با پایداری و کنترل، در این مطلب قصد داریم تا در مورد تابع لیاپانوف و کاربرد‌های آن صحبت کنیم. البته پیشنهاد می‌شود ابتدا به ساکن مطالب مفاهیم پایداری و اعداد مختلط را مطالعه فرمایید.

مقدمه

تابع لیاپانوف، تابعی اسکالر است که روی فضای فازی تعریف می‌شود. از این تابع به منظور بررسی پایداری یک نقطه استفاده می‌شود. روش تابع لیاپانوف در بررسی پایداری بسیاری از معادلات دیفرانسیل و سیستم‌ها کاربرد دارد.

در ابتدا سیستمی «خودگردان» (Autonomous) را به صورت زیر در نظر بگیرید.

$$\large { { \mathbf { X ^ { \prime } } = \mathbf { f } \left ( \mathbf { X } \right)\;\;\text{or}\;\;} \kern-0.3pt { \frac { { d { x _i } } } { { d t} } = { f _ i } \left( { { x_ 1 } , { x _2 } , \ldots ,{x_n}} \right),\;\;}\kern-0.3pt { i = 1,2, \ldots ,n,} }$$

که نقطه پایدار آن، $$X ≡ 0$$ است. فرض بر این است که تابعی پیوسته و مشتق‌پذیر به صورت زیر، در همسایگی $$U$$ به ما داده شده است.

$$\large V \left ( \mathbf { X } \right ) = V \left ( { { x_ 1 }, { x _2 } , \ldots , { x _n } } \right )$$

این تابع به ازای $$X ∈ U$$ مثبت بوده و در مبدا $$V \left ( \mathbf { 0 } \right ) = 0$$ است. برای نمونه توابع زیر نمونه‌ای از $$V$$ را نشان می‌دهند.

$$\large {V\left ( { { x_ 1 } ,{ x _ 2 } } \right ) = a x_1^2 + b x_ 2 ^ 2, \;\;} \\ \kern-0.3pt {V\left( { { x _ 1} , { x_ 2 } } \right ) = a x_ 1 ^ 2 + b x _2 ^ 4 ,\;\;}\kern-0.3pt { a , b \gt 0 }$$

در مرحله بعد مشتق کلی $$V$$ به صورت زیر قابل بیان است.

$$\large {\frac{ { dV } } { { d t } } = \frac{{\partial V}}{{\partial { x _ 1 } } } \frac{{d{x_1 } }} { {d t } } } + { \frac { { \partial V } } { { \partial { x _2 } } }\frac{{d{x_2 } }} { {d t } } + \cdots } + { \frac { { \partial V } } { { \partial { x _n } } }\frac { { d{ x _n } } } { { d t } } }$$

عبارت فوق را می‌توان به صورت ضرب داخلی دو بردار، به شکل زیر بیان کرد:

$$\large \begin {align*} { \frac { { d V } } { { d t } } = \left( {\text{grad}\,V,\frac{{d\mathbf{ X } } } {{ d t} } } \right) \;\;}\kern-0.3pt{\text{where}\;\;} & \kern-0.3pt {V = \left( { \frac{{\partial V } } { { \partial { x _1 } } } , \frac { { \partial V } } { {\partial {x _2 } } }, \ldots ,\frac{{\partial V } } { { \partial { x _ n} } } } \right) } \\\\ & \;\;{\frac { { d\mathbf { X } } } { { d t } } = \left( {\frac{{d{x_1 } }} { {d t } } ,\frac{{d { x_ 2 }} } {{ d t } }, \ldots ,\frac{{d { x _ n} } } { { d t } }} \right) } \end {align*}$$

در عبارت فوق، رابطه اول نشان دهنده گرادیان بردارِ $$V \left( \mathbf{X} \right)$$ است. این جهت نشان دهنده جهتِ بیشترین افزایش مقدار $$V$$ است. توجه داشته باشید که با افزایش $$X$$ به سمت بینهایت ($$\left| \mathbf { X } \right| \to \infty$$)، تابع $$V \left( \mathbf { X } \right )$$ نیز به صورت افزایشی تغییر می‌کند. بردار دوم در ضرب داخلی، نشان دهنده بردار سرعت است. در هر نقطه، این عبارت مماس بر مسیر فاز است.

حال حالتی را در نظر بگیرید که در آن مشتق $$V \left ( \mathbf { X } \right )$$ در همسایگی $$U$$ از مرکز، منفی باشد. گزاره زیر این حالت را نشان می‌دهد.

$$\large { \frac { { d V }} { { d t } } \text{ = }}\kern0pt{\left( {\text {grad}\,V,\frac{{d\mathbf { X } } }{ { dt } } } \right) }\lt { 0 }$$

این حالت نشان می‌دهد که زاویه بین $$\varphi$$ و بردار گرادیان و بردار سرعت، بیشتر از $$90^o$$ است. برای تابعی با دو متغیر، نمونه‌ای از این حالت از گرادیان در شکل زیر نشان داده شده است.

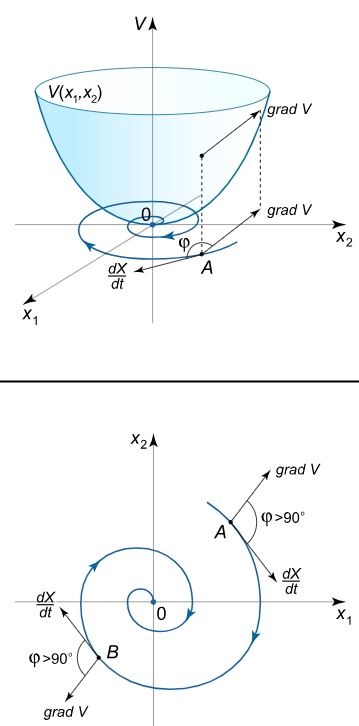
بدیهی است که اگر مشتق $$\frac { { d V } } { { d t } } \normalsize$$ در همه‌جا منفی باشد، در این صورت مسیر به مرکز نزدیک خواهد شد. در غیر این صورت در مواردی که مشتقِ $$\frac { { dV } } { { d t } } \normalsize$$ مثبت باشد، مسیر از مبدا دور خواهد شد. در چنین مواردی سیستم نیز ناپایدار است.

تابع $$V(X)$$ را با مشتقِ پیوسته مرتبه دوم در نزدیکی $$U$$ در نظر بگیرید. زمانی تابع $$V(X)$$، لیاپانوف تلقی می‌شود که شرایط زیر برای آن برقرار باشد.

• $$\large V \left( \mathbf { X } \right ) \gt 0$$
• $$\large V \left ( \mathbf { 0 } \right ) = 0$$
• $${ \large \frac { { d V } } { { d t } } \normalsize} \le 0$$

پایداری لیاپانوف

اگر $$U$$ تابع همسایه‌‌ نسبت به پاسخ $$X = 0$$ باشد، در این صورت تابع لیاپانوفی تحت عنوانِ $$V \left ( \mathbf { X } \right )$$ وجود خواهد داشت که مشتق آن نسبت به $$t$$ کمتر از صفر است. بنابراین می‌توان گزاره زیر را بیان کرد:

$${ \large\frac { { d V } }{ { d t} } \normalsize } \lt 0$$

با این فرضیات نقطه $$\mathbf { X } = \mathbf { 0 }$$، نقطه‌ای است که دارای پایداری مجانبی است.

ناپایداری لیاپانوف

اگر $$U$$ تابع همسایه‌‌ نسبت به پاسخ $$X = 0$$ باشد، تابعی مشتق‌پذیر و پیوسته‌ای هم‌چون $$V \left ( \mathbf { X } \right )$$ به نحوی وجود خواهد داشت که دو شرط زیر را خواهد داشت.

• $$V \left ( \mathbf { 0 } \right ) = 0$$
• $${ \large \frac { { d V } } { { d t } } \normalsize} \gt 0$$

حال می‌توان گفت که اگر در فضای همسایگیِ $$U$$ نقاطی وجود داشته باشند که در آن‌ها $$V \left ( \mathbf { X } \right ) \gt 0$$ باشد، در این صورت پاسخ صفرِ $$\mathbf { X } = \mathbf { 0 }$$ ناپایدار خواهد بود.

ناپایداری چتایف (Chetaev Instability)

فرض کنید $$U$$، فضای همسایگی پاسخ صفرِ $$X=0$$ باشد. در این صورت تابعی پیوسته و مشتق‌پذیر همچون $$V \left ( \mathbf { X } \right )$$ وجود خواهد داشت.

فیلم آموزش سیستم های کنترل غیر خطی با رویکرد حل مساله در فرادرس

کلیک کنید

حال فرض کنید $$U_1$$ و $$U_2$$ دو زیر دامنه از این فضا باشند؛ در این صورت ناحیه $$V$$ از ویژگی‌های زیر برخوردار خواهند بود.

1. $$V \left( \mathbf { X } \right ) \gt 0$$
2. به ازای تمامی مقادیر $$\mathbf { X } \in { U _ 1 } \backslash \left\{ \mathbf{ 0 } \right\}$$ تابع $$V$$ مثبت خواهد بود ($$V \left( \mathbf { X } \right ) \gt 0$$).
3. به ازای تمامی مقادیرِ $$\mathbf { X } \in \delta { U _ 1 } ,$$، مقدار تابع $$\mathbf { V } ( \mathbf X) =0$$ است. توجه داشته باشید که $$\delta { U _1 }$$ نشان دهنده مرز‌های زیر مجموعه $$U_1$$ است. در این صورت پاسخ صفرِ $$\mathbf { X } = \mathbf { 0 }$$ این سیستم، ناپایدار خواهد بود. در این حالت مسیر فاز‌های مربوط به زیر مجموعه $${ U _ 1 }$$، از مرکز دور خواهند شد.

در شکل زیر نمونه‌ای از چنین ناحیه‌ایی نشان داده شده است.

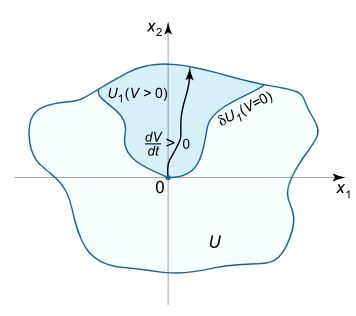
نهایتا می‌توان گفت که توابع لیاپانوف می‌توانند تعیین کننده پایداری یا ناپایداری یک سیستم باشند. مزیت این روش این است که نیازی نیست الزما پاسخ واقعی $$\mathbf { X } \left ( t \right )$$ را بدانیم. علاوه بر این، این روش شرایطی را به منظور مطالعه نقطه تعادل یک سیستم فراهم می‌کند. در ادامه به منظور درک بهتر مثال‌هایی ارائه شده که پیشنهاد می‌شود آن‌ها را مطالعه فرمایید.

مثال ۱

پایداری پاسخ صفر معادله زیر را بدست آورید.

$$\large { \frac { { d x } } { { d t } } = – 2 x \; ,\;\;} \kern-0.3pt { \frac { { dy } } {{ d t } } = x – y }$$

این سیستم، یک سیستم خطی همگن با ضرایب ثابت است. تابع لیاپانوف را به صورت زیر، از مرتبه دو تعریف می‌کنیم.

$$\large { V \left ( \mathbf { X } \right ) = V \left ( { x , y } \right ) } = { a { x ^ 2 } + b { y ^ 2 } }$$

توجه داشته باشید که ضرایب $$a , b$$ باید با استفاده از مشتق مادی، به صورت زیر محاسبه شوند. همان‌طور که در بالا نیز بیان شد، تابع $$V \left ( { x , y } \right )$$ در تمامی نقاط به جز مرکز مثبت است. در ابتدا مشتق مادی $$V$$ را به صورت زیر محاسبه می‌کنیم.

$$\large \begin {align*} { \frac { { d V } }{ { d t } } } & = \kern0pt { \frac { { \partial V } } { { \partial x } } \frac { { d x } } { {d t } } + \frac { { \partial V } } { { \partial y } } \frac { { d y } } { { d t } } } \\\\ & = { 2 a x \left ( { – 2 x } \right ) + 2 b y \left ( { x – y } \right ) } \\\\ & = { – 4 a { x ^ 2 } + 2 b x y – 2 b { y ^ 2 } } \\\\ & = { – 2 b \left ( { \frac { { 4 a } } { {2 b } } { x ^ 2 } – x y + { y ^ 2 } } \right ) } \\\\ & = { – 2 b \left ( { \frac { { 2 a } } { b } { x^ 2 } – x y + { y ^ 2} } \right ) } \end {align*}$$

عبارت قرار گرفته در براکت را می‌توان به صورت مربع کامل نوشت، اگر رابطه زیر بین ضرایب $$b$$ , $$a$$ برقرار باشد.

$$\large \frac { { 2 a } } { b } = \frac { 1 } { 4 } \;\;\text{or}\;\; 8 a = b$$

برای نمونه اگر $$a=1$$ و $$b=8$$ باشد، رابطه جبری بالا را می‌توان به صورت مربع کامل، به شکل زیر بیان کرد:

$$\large { \frac { { d V } } { { d t } } \text{ = }}\kern0pt{ – 16\left( {\frac { { { x ^ 2 } } } { 4 } – x y + { y ^ 2 } } \right) } = { – 16{\left( {\frac { x } { 2 } – y} \right ) ^ 2 } \lt 0 }$$

بنابراین برای سیستم ارائه شده، تابعی از جنس لیاپانوف پیدا شده که مشتقات آن در تمامی نقاط به جز مرکز، منفی هستند. از این رو پاسخ صفر سیستم، به صورت مجانبی پایدار است.

مثال ۲

پایداری پاسخ صفر سیستم زیر را تعیین کنید.

$$\large { \frac { { d x } } { { d t } } = y \; \; ,\;\;} \kern-0.3pt { \frac { { d y } } { { d t } } = – x }$$

به دلیل مرکز بودنِ پاسخِ صفر، بررسی پایداری به روش تقریب مرتبه اول، امکان‌پذیر نیست. هم‌چنین معادله مشخصه ماتریس ضرایب برابرند با:

$$ \large \begin {align*} A & = \left [ {\begin{array}{*{20} { r } } 0 &1 \\ { – 1}&0 \end {array}} \right] \kern-0.3pt {\det \left( {A – \lambda I} \right) = 0 \;\; } \\\\ & \Rightarrow {\left| {\begin {array} {*{20} { c } } { – \lambda } & 1 \\ { – 1 } & { – \lambda } \end{array} } \right| = 0 \;\; } \\\\ & \Rightarrow { { \lambda ^ 2 } + 1 = 0 \;\; } \Rightarrow { { \lambda _ { 1 , 2 } } = \pm i } \end {align*} $$

در قدم بعد به منظور استفاده از روش لیاپانوف، تابع آن را به صورت زیر در نظر می‌گیریم.

$$\large { V \left ( \mathbf { X } \right ) = V \left( { x ,y } \right ) } = { { x ^ 2 } + { y ^ 2 } }$$

بنابراین مشتق مادی تابع در نظر گرفته شده برابر است با:

$$\large { V \left ( \mathbf { X } \right ) = V \left ( { x , y } \right ) } = { { x ^ 2 } + { y ^ 2 } }$$

همان‌طور که حاصل مشتق نیز نشان می‌دهد، مقدار آن برابر با صفر است. بنابراین $$V \left ( \mathbf { X } \right )$$ تابعی لیاپانوف محسوب شده و پاسخ صفر سیستم از نظر لیاپانوف پایدار است. توجه داشته باشید که شرایط مربوط به پایداری مجانبی در این مسئله وجود ندارد.

مثال ۳

پایداری پاسخ صفر سیستم غیرخطی زیر را بررسی کنید.

$$\large { \frac { { d x } } { { d t } } = – x { y ^ 2 } \; ,\;\;} \kern-0.3pt { \frac { { d y } } { { d t } } = 3 y { x ^ 2 } }$$

واضح است که ژاکوبین سیستم در نقطه $$( 0 , 0 )$$ ماتریس صفر زیر است.

$$ \large {\require {AMSmath.js}<br /> { J = { \left. {\left[ {\begin{array}{*{20}{c}}<br /> { \frac { { \partial { f _1 } } } { { \partial x } } } & {\frac{{\partial { f _ 1 } } }{ { \partial y } } } \\ {\frac{{\partial { f _ 2 } } } { { \partial x } } } &{\frac { { \partial { f _ 2} } } { { \partial y } } } \end{array}} \right]} \right|_{\substack{<br /> x = 0 \\ y = 0 } } } }={ \left[ {\begin {array}{*{20}{c}}<br /> 0 & 0 \\ 0 & 0 \end {array}} \right] } } $$

مقادیر ویژه ماتریس فوق برابر با صفر هستند. بنابراین بررسی پایداری با استفاده از تقریب مرتبه اول امکان‌پذیر نخواهد بود. از این رو از پایداری لیاپانوف به منظور بررسی پایداری سیستم استفاده می‌کنیم.

بدین منظور در ابتدا تابع لیاپانوف را به صورت زیر در نظر می‌گیریم.

$$\large V \left ( \mathbf { X } \right ) = V \left ( { x , y } \right ) = 3 { x ^ 2 } + { y ^ 2 }$$

تابع فوق در تمامی نواحی به جز مرکز مثبت مطلق است. همچنین مشتق مادی آن برابر است با:

$$\large \begin {align*} \frac { { d V } } { { d t } } \text{ } & = \kern0pt { \frac { { \partial V } } { { \partial x } } \frac { { d x } } { { d t } } + \frac{{\partial V } } { { \partial y } } \frac{{ d y } }{ { d t}} } \\\\ & = {6x\left ( { – x{y^2}} \right) + 2y\left( { 3 y { x ^ 2 } } \right) } \\\\ & = { – 6 { x ^ 2 } {y ^ 2 } + 6 { x ^ 2 }{ y ^ 2 } } \equiv{ 0 } \end {align*}$$

همچون مثال‌های قبل می‌بینید که مشتق نیز برابر با صفر است، بنابراین معادله نیز پایدار است.

مثال ۴

پایداری پاسخ صفر سیستم زیر را استفاده از تابع لیاپانوف بررسی کنید.

$$\large { \frac { { d x} } { { d t } } = y – 2 x \; ,\;\;} \kern-0.3pt { \frac { { dy } } {{ d t } } = 2 x – y – { x ^ 3 } }$$

تابع لیاپانوف را مطابق با عبارت زیر انتخاب می‌کنیم.

$$\large { V \left ( \mathbf { X } \right ) = V \left ( { x , y } \right ) } = { { \left ( { x + y } \right ) ^ 2 } + \frac { { { x ^ 4 } } } { 2 } }$$

بدیهی است که تابع در نظر گرفته شده در تمامی نقاط به جز مرکز، مثبت است. از این رو مشتق آن را به شکل زیر محاسبه می‌کنیم.

$$ \large \begin {align*} \require {cancel} { \frac { { d V } } { {d t } } \text { } } & = \kern0pt{\frac { { \partial V } } { { \partial x } } \frac{ { d x} } { { dt }} + \frac { { \partial V}}{{\partial y}}\frac{ {d y } } {{ d t } } } \\ & = {{\left( {2x + 2y + 2{ x ^3 } } \right)\left( {y – 2x} \right) }}+{{ \left( {2x + 2y} \right)\left( {2x – y – { x ^3 } } \right) }} \\ & = {{\cancel{\left( {2x + 2y} \right)\left( {y – 2x} \right)} }+{ 2 {x ^ 3 }\left( {y – 2x} \right) }} – {{\cancel{\left( {2x + 2y} \right)\left( {y – 2 x } \right)} } } - { { { x ^ 3 } \left( {2x + 2y} \right) }} \\ & = {{\cancel{ 2 { x^ 3 } y } – 4{x^4} }-{ 2{x^4} – \cancel { 2 { x ^3 } y} } } \\ & = { – 6 {x ^ 4 } \le 0 } \end {align*} $$

همان‌طور که می‌توان دید حاصل مشتق نیز در تمامی نقاط به جز $$\left ( { 0 , 0 } \right )$$ منفی است. بنابراین پاسخ صفر این معادله، دارای پایداری مجانبی است. با استفاده از پایداری مرتبه اول، می‌توان دید نقطه صفر نیز پایدار است. عملا مقادیر ویژه سیستم خطی، اعداد مختلطی با مقادیر حقیقی منفی هستند. در ادامه مقادیر ویژه ماتریس ضرایب محاسبه شده‌اند.

$$ \large \begin {align*} { J = \left[ { \begin {array} {*{20}{r}}<br /> 1 & { – 2 } \\ 2 & { – 1} \end {array} } \right],\;\;} & \kern-0.3pt<br /> {\det \left( {J – \lambda I} \right) = 0,\;\;} \\ & \Rightarrow { \left| {\begin{array}{*{20}{c}} {1 – \lambda }&{ – 2} \\ 2&{ – 1 – \lambda } \end{array}} \right| = 0,\;\;} \\ & \Rightarrow {{\left( {\lambda + 1} \right)^2} + 4 = 0,\;\;} \\ & \Rightarrow {{\left( {\lambda + 1} \right ) ^ 2 } = – 4,\;\;} \Rightarrow { \left| { \lambda + 1} \right| = \pm 2i \;\; } \\ & \Rightarrow { { \lambda _{ 1 , 2 } } = – 1 \pm 2 i } \end {align*} $$

مثال ۵

پایداری پاسخ صفر سیستم زیر را بررسی کنید.

$$\large { \frac { { d x } } { { d t } } = { x ^ 3 } + y \; ,\;\;} \kern-0.3pt { \frac { { dy } } { { d t } } = x + { y ^ 3 } }$$

همان‌طور که می‌توان از سمت راست معادله دید، مشتقاتِ $${ \frac { { dx } }{ { d t} } \normalsize }$$، $${ \frac { { d y } } { { d t } } \normalsize }$$ برای نقاط قرار گرفته در ربع اول دستگاه مختصات، مثبت هستند. از این رو سیستم به ازای نقاط قرار گرفته در این قسمت ناپایدار است. بنابراین این مسئله را می‌توان با استفاده از ناپایداری چتایف تحلیل کرد. نهایتا تابع $$V$$ را به صورت زیر در نظر می‌گیریم.

$${ V \left( \mathbf { X } \right ) = V \left ( { x , y } \right ) } = { { x ^ 2 } – { y ^ 2 } }$$

این تابع در ناحیه‌ای از فضا که در آن نامساوی $$\left| x \right| \gt \left| y \right|$$ برقرار است، مثبت است. در شکل زیر این ناحیه نشان داده شده است.

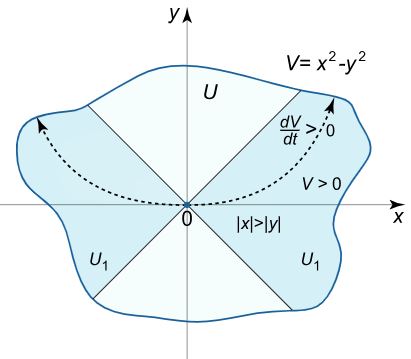
مشتقِ $${ \frac { { d V } } { { d t } } \normalsize }$$ برابر است با:

$$\large \begin {align*} {\frac { {d V } } { {d t } } \text{ }} & = \kern0pt {\frac { { \partial V } } { { \partial x } } \frac{{ d x } } { { d t } } + \frac { { \partial V } } { { \partial y } } \frac { {d y } } { { dt } } } \\\\ & = { 2 x \left( { { x ^ 3 } + y} \right ) – 2 y \left ( {x + {y^3 } } \right ) } \\\\ & = { 2 { x ^ 4 } + \cancel { 2 x y } – \cancel { 2 x y } – 2 { y ^ 4 } } \\\\ & = { 2 \left( { { x ^ 4 } – { y ^ 4 } } \right ) } \end {align*}$$

همان‌طور از رابطه فوق بر می‌آید این مشتق در ناحیه $$\left| x \right| \gt \left| y \right|.$$ مثبت است. از طرفی خود تابع $$V$$ نیز روی مرز‌ها و نقطه $$(0,0)$$ برابر با صفر است. بنابراین تمامی شرایط به منظور بررسی پایداری از دیدگاه چتایف برای این مسئله وجود دارد. بنابراین پاسخ صفرِ این سیستم ناپایدار است.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی و کنترل آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های مهندسی کنترل
• مجموعه آموزش‌‌های ریاضی
• مفاهیم پایداری — از صفر تا صد
• مشتق — به زبان ساده
• انتگرال — به زبان ساده

^^