دامنه توابع رادیکالی – نحوه تعیین به زبان ساده + مثال و تمرین

توابع زیر، مثال‌های تابع رادیکالی هستند:

$$ f ( x ) = \sqrt { x } $$

$$ f ( x ) = \sqrt [ ۳ ] { x } $$

$$ f ( x ) = \sqrt { x ^ { ۲ } + ۱۰ } $$

$$ f ( x ) = ۲ \sqrt { x + ۴ } $$

$$ f ( x ) = - \sqrt { x } - ۲ $$

$$ f ( x ) = -۲ + \sqrt { x + ۵ } $$

$$ f ( x ) = ۷ + \sqrt [ ۴ ] { ( x +۱ ) ^ ۳ } $$

$$ f ( x ) = \sqrt { \frac { e ^ x } { x ^ ۲ - ۳ x } } $$

$$ f ( x ) = \frac { | x ^ ۳ - \frac { x } { ۲ } |} { \sqrt [ ۳ ] {۲ \sin ( x ) } } $$

به عدد پشت رادیکال، فرجه می‌گویند. در توابع رادیکالی با فرجه زوج، $$ x $$ نمی‌تواند هر مقدار دلخواهی باشد. به عنوان مثال، تابع $$ f ( x ) = \sqrt { x } $$ را در نظر بگیرد. اگر مقدار $$ x $$ برابر با عددی کوچک‌تر از ۰ باشد، عدد زیر رادیکال منفی شده و خروجی تابع، تعریف نشده می‌شود. برای درک این موضوع، مفهوم رادیکال را به خاطر بیاورید. رادیکال، عکس توان عمل می‌کند. به عنوان مثال، اگر عدد ۲ را به توان دو برسانیم، عدد ۴ به دست می‌آید:

$$ ۲ ^ ۲ = ۴ $$

در طرف مقابل، اگر عدد ۴ را زیر رادیکال ببریم، به عدد ۲ می‌رسیم:

$$ \sqrt { ۴ } = ۲ $$

خروجی رادیکال (۲)، عددی است که مربع آن ($$ ۲ ^ ۲ $$)، برابر با عدد زیر رادیکال (۴) شود. بنابراین، اگر یک عدد منفی مانند ۴- را زیر رادیکال ببریم، هیچ خروجی تعریف شده‌ای به دست نمی‌آید. زیرا نمی‌توانیم عددی را پیدا کنیم که مربع آن برابر با ۴- باشد. مفهوم رادیکال، اهمیت بالایی در تعیین دامنه توابع مختلف دارد. در واقع، رادیکالی بودن عبارت‌های تابع، یکی از مواردی است که هنگام تعیین محدودیت‌های دامنه مورد بررسی قرار می‌گیرد.

رادیکال چیست ؟ — قوانین رادیکال به زبان ساده

فیلم آموزش حسابان ۱ – پایه یازدهم در فرادرس

دامنه توابع رادیکالی چیست؟

دامنه تابع رادیکالی، مجموعه مقادیری است که با قرار دادن هر یک از آن‌ها درون رابطه تابع، به یک مقدار مشخص (مقدار تعریف شده) دست پیدا می‌کنیم. به عنوان مثال، تابع $$ f ( x ) = \sqrt { x ^ { ۲ } + ۱۰ } $$ را در نظر بگیرید.

اگر مقدار $$ x $$ در این تابع، برابر با اعداد بزرگ‌تر یا مساوی ۱۰- باشد ($$ x \ge - ۱۰ $$)، خروجی تابع یک مقدار تعریف شده خواهد بود:

تعریف شده $$ f ( - ۱۰ ) = \sqrt { - ۱۰ + ۱۰ } = \sqrt { ۰ } = ۰ \implies $$

تعریف شده $$ f ( - ۵ ) = \sqrt { - ۵ + ۱۰ } = \sqrt { ۵ } \implies $$

تعریف شده $$ f ( ۶ ) = \sqrt { ۶ + ۱۰ } = \sqrt { ۱۶ } = ۴ \implies $$

در صورتی که $$ x $$های کوچک‌تر از ۱۰- را درون تابع قرار دهیم، به مقادیر تعریف شده نمی‌رسیم:

تعریف نشده $$ f ( - ۱۱ ) = \sqrt { - ۱۱ + ۱۰ } = \sqrt { - ۱ } \implies $$

تعریف نشده $$ f ( - ۱۵ ) = \sqrt { - ۱۵ + ۱۰ } = \sqrt { - ۵ } \implies $$

تعریف نشده $$ f ( - ۲۳ ) = \sqrt { - ۲۳ + ۱۰ } = \sqrt { - ۱۳ } \implies $$

عبارت‌های زیر رادیکال با فرجه زوج نمی‌توانند منفی باشند. بنابراین، مجموعه اعدادی که با قرار دادن آن‌ها در تابع، عبارت زیر رادیکال، بزرگ‌تر از ۰ شود، به عنوان دامنه تابع رادیکالی $$ f ( x ) = \sqrt { x ^ { ۲ } + ۱۰ } $$ در نظر گرفته می‌شود. به عبارت دیگر، دامنه $$ f ( x ) $$ از $$ - ۱۰ $$ تا $$ + \infty $$ است.

هنگام تعیین دامنه توابع رادیکالی، باید به زوج یا فرد بودن فرجه رادیکال توجه کرد. فرجه $$ \sqrt { x ^ { ۲ } + ۱۰ } $$ برابر با ۲ است. اگر این فرجه برابر با ۳ می‌بود، دیگر محدودیتی برای مقادیر $$ x $$ وجود نمی‌نداشت (دامنه از $$ - \infty $$ تا $$ + \infty $$ می‌شد).

دامنه و برد توابع جبری و گویا — به زبان ساده

فیلم آموزش حسابان ۱ – پایه یازدهم – حل تمرین در فرادرس

مثال ۱: تعیین دامنه توابع رادیکالی با فرجه ۲

توابع زیر را در نظر بگیرید:

$$ f ( x ) = \sqrt { - x } $$

$$g ( x ) = \sqrt { x ^ ۲ - ۱ }$$

$$ h ( x ) = \sqrt { x ^ { ۲ } + ۱۰ } $$

می‌خواهیم دامنه توابع بالا را بر اساس تعریف دامنه توابع رادیکالی به دست بیاوریم. فرجه تمام این توابع برابر با ۲ است. طبق تعریف، مقادیر زیر رادیکال با فرجه زوج نباید منفی (کوچکتر از ۰) باشند.

دامنه $$ f ( x ) = \sqrt { - x } $$

به منظور تعیین دامنه $$ f ( x ) = \ sqrt { - x } $$، باید از خود بپرسیم که با قرار دادن چه مقادیری از $$ x $$، خروجی تابع $$ f ( x ) $$، بزرگ‌تر یا مساوی ۰ می‌شود. اگر مقدار $$ x $$ را برابر با ۰ قرار دهیم، خواهیم داشت:

$$ x = ۰ \implies f ( x ) = \sqrt { - ۰ } = ۰ $$

همان‌طور که مشاهده می‌کنید، خروجی تابع برای $$ x $$، یک مقدار مشخص و برابر با ۰ شد. اکنون، $$ x $$ را برابر با یک عدد منفی مانند ۱- در نظر می‌گیریم و تابع $$ f ( x ) $$ را به دست می‌آوریم:

$$ x = - ۱ \implies f ( x ) = \sqrt { - ( - ۱ ) } = \sqrt { +۱ } = ۱ $$

با قرار دادن یک عدد منفی در تابع نیز به یک عدد مشخص رسیدیم. در نهایت، یک عدد مثبت مانند ۱+ را درون تابع جایگذاری می‌کنیم:

تعریف نشده $$ x = + ۱ \implies f ( x ) = \sqrt { - ( + ۱ ) } = \sqrt { - ۱ } \implies $$

در این حالت، خروجی تابع «تعریف نشده» است؛ زیرا جوابی برای رادیکال یک عدد منفی وجود ندارد. با بررسی اعداد مختلف، به این نتیجه خواهیم رسید که دامنه $$ f ( x ) = \ sqrt { - x } $$، مقادیر ۰ تا $$ - \infty $$ است.

دامنه $$ g ( x ) = \sqrt { x ^ ۲ - ۱ } $$

برای تعیین دامنه $$ g ( x ) = \sqrt { x ^ ۲ - ۱ } $$، باید مقادیری را به دست بیاوریم که با قرار دادن آن‌ها در تابع، حاصل عبارت زیر رادیکال مثبت شود. به عبارت دیگر، باید به دنبال $$ x $$هایی باشیم که شرط زیر را محقق کنند:

$$ x ^ ۲ - ۱ \ge ۰ $$

$$ - ۱ $$ را به طرف راست می‌بریم:

$$ x ^ ۲ \ge ۱ $$

نامساوی بالا، معیار تعیین دامنه تابع مورد سوال است. اگر x را برابر با ۱ یا هر عدد بزرگ‌تر از آن ( ۱ تا $$ + \infty $$) قرار دهیم، شرط بالا برقرار می‌شود. به عنوان مثال:

$$
x = + ۲ \implies ۲ ^ ۲ = ۴ \ge ۱ \ \ \ \ \ \ \checkmark
$$

قرار دادن ۱- و اعداد کوچکتر از آن (۱- تا $$ - \infty $$) به جای x نیز باعث برقراری شرط بالا می‌شود. به عنوان مثال:

$$
x = - ۳ \implies ( - ۳ ) ^ ۲ = ۹ \ge ۱ \ \ \ \ \ \ \checkmark
$$

اکنون، $$ x $$ را برابر با عددی مثبت و کوچک‌تر از ۱+ قرار می‌دهیم:

$$
x = ۰/۵ \implies ( ۰/۵ ) ^ ۲ = ۰/۲۵ \ge ۱ \ \ \ \ \ \ \times
$$

در مرحله آخر، یک عدد منفی و بزرگ‌تر از ۱- را جایگزین $$ x $$ می‌کنیم:

$$
x = ۰/۵ \implies ( - ۰/۲ ) ^ ۲ = ۰/۰۴ \ge ۱ \ \ \ \ \ \ \times
$$

همان‌طور که مشاهده می‌کنید، برای مقادیر بین ۱- تا ۱+، شرط برقرار نمی‌شود. از این‌رو، دامنه تابع $$ g ( x ) = \sqrt { x ^ ۲ - ۱ } $$، مقادیر بزرگ‌تر مساوی ۱+ (۱+ تا $$ + \infty $$) و کوچک‌تر از ۱- (۱- تا $$ - \infty $$) خواهد بود.

دامنه تابع $$ h ( x ) = \sqrt { x ^ { ۲ } + ۱۰ } $$

اعضای دامنه تابع $$ h ( x ) = \sqrt { x ^ { ۲ } + ۱۰ } $$، اعدادی هستند که با قرار دادن آن‌ها در $$ h ( x ) $$، عبارت زیر رادیکال، بزرگ‌تر یا مساوی با صفر می‌شود. به عبارت دیگر، مقادیر دامنه این تابع رادیکالی در نامساوی زیر صدق می‌کنند:

$$ \sqrt { x ^ { ۲ } + ۱۰ } \ge ۰ $$

یا

$$ \sqrt { x ^ { ۲ } } \ge - ۱۰ $$

$$ x ^ ۲ $$، همواره مثبت است. بنابراین، عبارت زیر رادیکال ($$ x ^ ۲ + ۱۰ $$)، هیچگاه کوچک‌تر از صفر نمی‌شود.

در نتیجه، هیچ محدودیتی برای دامنه تابع $$ h ( x ) $$ وجود نخواهد داشت و بازه این دامنه بین $$ - \infty $$ تا $$ + \infty $$ خواهد بود. در بخش بعدی، نحوه به دست آوردن توابع رادیکالی را به طور جزئی‌تر آموزش می‌دهیم.

دامنه توابع رادیکالی چگونه بدست می آید؟

دامنه توابع رادیکالی با توجه خواص رادیکال به دست می‌آید. یک عدد رادیکالی مانند $$ \sqrt [ r ] { a } $$ را در نظر بگیرید. r، فرجه یا ریشه رادیکال و a، یک عدد حقیقی را نمایش می‌دهد.

فیلم آموزش ریاضی ۲ – پایه یازدهم علوم تجربی در فرادرس

اگر r برابر با یک عدد زوج ($$ r = ۲ n $$) باشد، دو حالت پیش می‌آید.

a، بزرگ‌تر یا مساوی ۰ (مثبت یا صفر) است. در این حالت، $$ \sqrt [ r ] { a } $$، عضوی از مجموعه اعداد حقیقی خواهد بود.
a، کوچک‌تر از ۰ (منفی) است. در این حالت، $$ \sqrt [ r ] { a } $$، عضوی از مجموعه اعداد حقیقی نخواهد بود.

اگر r برابر با یک عدد فرد ($$ r = ۲ n + ۱ $$) باشد، $$ \sqrt [ r ] { a } $$ همواره عضوی از مجموعه اعداد حقیقی خواهد بود. نکاتی که تا به اینجا گفتیم به صورت زیر خلاصه می‌شوند:

$$ a \ge ۰ \ \implies \sqrt [ ۲ n ] {a} \in R $$

$$ a \lt ۰ \ \implies \sqrt [ ۲ n ] {a} \notin R $$

$$ \sqrt [ ۲ n + ۱] {a} \in R $$

با توجه به این خواص، اولین قدم در تعیین دامنه توابع رادیکالی، بررسی زوج یا فرد بودن فرجه است. اگر فرجه فرد بود، عبارت زیر رادیکال می‌تواند هر عدد حقیقی دلخواهی باشد. در صورت زوج بودن فرجه، مقدار عبارت زیر رادیکال به اعداد ۰ تا $$ + \infty $$ محدود می‌شود.

به عنوان مثال، تابع $$ f ( x) = \sqrt { ۳ x - ۴ } $$ را در نظر بگیرید. $$ f ( x ) $$ یک تابع خطی را زیر رادیکال با فرجه ۲ نمایش می‌دهد. به دلیل زوج بودن فرجه رادیکال، عبارت زیر آن نمی‌تواند منفی باشد. بنابراین، باید عبارت زیر رادیکال را بزرگ‌تر یا مساوی صفر قرار دهیم:

$$ ۳ x - ۴ \ge ۰ $$

با حل این نامساوی بر حسب $$ x $$، دامنه $$ f ( x ) $$ به دست می‌آید. به این ترتیب، داریم:

$$
\begin {aligned} ۳ x - ۴ & \geq ۰ \\ ۳ x & \geq ۴ \\ x & \geq \frac { ۴ } { ۳ } \end {aligned}
$$

در نتیجه، دامنه $$ f ( x) = \sqrt { ۳ x - ۴ } $$، تمام مقادیر $$ x \geq \frac { ۴ } { ۳ } $$ است. این دامنه به صورت زیر نوشته می‌شود:

$$
D: \left \{ x | x \in \left [ \frac { ۴ } { ۳ }, \ + \infty \right ) \right \}
$$

علامت «$$ [ $$»، یعنی عدد $$ \frac { ۴ } { ۳ } $$ در بازه دامنه قرار می‌گیرد و $$ x $$ می‌تواند برابر با این عدد باشد. اگر به جای $$ [ $$ از پرانتز «$$ ( $$» استفاده می‌کردیم، $$ x $$ نمی‌توانست دقیقا برابر با $$ \frac { ۴ } { ۳ } $$ شود. محور اعداد، ابزار بسیار مناسبی برای نمایش و درک محدوده دامنه توابع مختلف، مخصوصا توابع رادیکالی است.

$$
_{- \infty }\text { <—|—|—|—}_۰\text{—|—|—|—>}_ {+ \infty}
$$

بازه دامنه تابع $$ f ( x) = \sqrt { ۳ x - ۴ } $$ را می‌توان مانند تصویر زیر بر روی محور اعداد نشان داد.

مثال ۲: تعیین دامنه تابع خطی زیر رادیکال با فرجه زوج و فرد

توابع زیر را در نظر بگیرید:

$$ f ( x ) = \sqrt [ ۴ ] { ۶ x - ۵ } $$

$$ g ( x ) = \sqrt [ ۵ ] { ۴ - ۵ x } $$

برای به دست آوردن دامنه توابع بالا، ابتدا به فرجه عبارت رادیکالی آن‌ها دقت می‌کنیم. فرجه $$ \sqrt [ ۴ ] { ۶ x - ۵ } $$، یک عدد زوج (۴) است. بنابراین، عبارت زیر رادیکال نمی‌تواند منفی باشد:

$$
\begin {aligned} ۶ x - ۵ & \geq ۰ \\ ۶ x & \geq ۵ \\ x & \geq \frac { ۵ } { ۶ } \end {aligned}
$$

$$ x $$ در $$ f ( x ) $$، می‌تواند بزرگ‌تر یا مساوی $$ \frac { ۵ } { ۶ } $$ باشد. در نتیجه، برای دامنه $$ f ( x ) = \sqrt [ ۴ ] { ۶ x - ۵ } $$ داریم:

$$
D _ { f ( x ) } : \left\{ x | x \in \left [ \frac { ۵ } { ۶ }, \ + \infty \right ) \right \}
$$

فرجه $$ \sqrt [ ۵ ] { ۴ - ۵ x } $$، یک عدد فرد (۵) است. از این‌رو، عبارت زیر رادیکال می‌تواند مثبت، منفی یا صفر باشد. در نتیجه، دامنه $$ g ( x ) = \sqrt [ ۵ ] { ۴ - ۵ x } $$ به صورت زیر نوشته می‌شود:

$$
D _ { g ( x ) } : \left\{ x | x \in \left ( - \infty , \ + \infty \right ) \right \}
$$

دامنه تابع رادیکالی کسری

«تابع کسری» (Quotient Function)، یکی دیگر از انواع توابع ریاضی است که از تقسیم دو تابع به وجود می‌آید. در توابع کسری، مخرج کسر نمی‌تواند برابر با صفر باشد. از این‌رو، باید مقادیری که باعث صفر شدن مخرج کسر می‌شوند را از مجموعه دامنه توابع کسری خارج کرد.

فیلم آموزش حسابان ۱ – پایه یازدهم در فرادرس

به عنوان مثال، $$ g ( x ) = \sqrt { \frac { ۶ } { x - ۱ } } $$ را در نظر بگیرید. این تابع، یک تابع کسری زیر رادیکال را نمایش می‌دهد. تابع کسری زیر رادیکال را برابر با $$ f ( x ) $$ قرار می‌دهیم:

$$ f ( x ) = \frac { ۶ } { x - ۱ } $$

می‌دانیم که مخرج توابع کسری نمی‌تواند برابر با ۰ شود. از این‌رو، داریم:

$$ x - ۱ \ne ۰ $$

نامساوی بالا را بر حسب $$ x $$ حل می‌کنیم:

$$ x \ne ۱ $$

در تابع $$ f ( x ) $$ مقدار $$ x $$ می‌تواند هر عددی به غیر از ۱ باشد. بنابراین:

$$
D _ { f ( x ) }: \left\{ x | x \in \left ( - \infty , ۱ \right) \cup \left ( ۱ , + \infty \right ) \right \}
$$

یا

$$
D _ { f ( x ) }: \left\{ x | x \in \left ( - \infty , + \infty \right), \ x \ne ۱ \right \}
$$

اکنون به سراغ دامنه تابع $$ g ( x ) $$ می‌‌رویم. برای سادگی بیشتر، این تابع را به صورت زیر بازنویسی می‌کنیم:

$$
g ( x ) = \sqrt { \frac { ۶ } { x - ۱ } } = \frac { \sqrt { ۶} }{ \sqrt { x - ۱ }}
$$

مخرج تابع بالا، از یک عبارت رادیکالی با فرجه دو تشکیل می‌شود. به دلیل زوج بودن فرجه رادیکال، عبارت زیر آن نمی‌تواند کوچک‌تر از ۰ باشد. از این‌رو، داریم:

$$
x - ۱ \ge ۰
$$

این نامساوی را بر حسب $$ x $$ حل می‌کنیم:

$$
x \ge ۱
$$

بنابراین، دامنه $$ \sqrt { x - ۱ } $$، مجموعه مقادیر بزرگ‌تر یا مساوی با ۱ است. این دامنه به صورت زیر نوشته می‌شود:

$$ D : \left\{ x | x \in \left [ ۱ , + \infty \right ) \right \} $$

دامنه $$ f ( x ) $$ را با دامنه بالا مقایسه کنید:

$$
D _ { f ( x ) }: \left\{ x | x \in \left ( - \infty , ۱ \right) \cup \left ( ۱ , + \infty \right ) \right \}
$$

دامنه $$ g ( x ) $$، مجموعه اعدادی است که در هر دو دامنه بالا صدق کند. همان‌طور که مشاهده می‌کنید، بازه مشترک بین دامنه کسر زیر رادیکال و تابع رادیکالی مخرج، مجموعه اعداد بزرگ‌تر از ۱ است. در نتیجه:

$$
D _ { g ( x ) } : \left\{ x | x \in \left ( ۱ , + \infty \right ) \right \}
$$

دقت داشته باشید که عدد ۱ در دامنه $$ g ( x ) = \sqrt { \frac { ۶ } { x - ۱ } } $$ قرار ندارد. برای اطمینان از صحت نتیجه به دست آمده، یک عدد از مجموعه دامنه (مانند ۲) و یک عدد خارج از مجموعه دامنه (مانند ۰) را درون تابع قرار می‌دهیم و وجود یا عدم وجود خروجی را بررسی می‌کنیم:

$$
g ( ۲ ) = \sqrt { \frac { ۶ } { ۲ - ۱ } } = \sqrt { \frac { ۶ } { ۱ } } = \sqrt { ۶ }
$$

$$
g ( ۲ ) = \sqrt { ۶ } \ \ \ \ \ \checkmark
$$

$$
g ( ۰ ) = \sqrt { \frac { ۶ } { ۰ - ۱ } } = \sqrt { \frac { ۶ } { - ۱ } } = \sqrt { - ۶ }
$$

$$
g ( ۰ ) = \sqrt { - ۶ } \ \ \ \ \ \times
$$

مثال ۳: دامنه توابع رادیکالی در مخرج

تابع کسری زیر را در نظر بگیرید:

$$ f ( x ) = \frac { ۱ } { \sqrt { x } } $$

با توجه به خواص توابع کسری، مخرج این تابع ($$ \sqrt { x } $$) نمی‌تواند برابر با ۰ باشد. بنابراین، اولین محدودیت برای تعیین دامنه $$ f ( x ) $$، به صورت زیر نوشته می‌شود:

$$ \sqrt { x } \ne ۰ $$

اگر هر دو طرف نامساوی زیر را به توان ۲ برسانیم، خواهیم داشت:

$$ x \ne ۰ $$

به این ترتیب، عدد ۰ از مجموعه دامنه تابع حذف می‌شود. تابع کسری $$ f ( x ) = \frac { ۱ } { \sqrt { x } } $$، یک تابع رادیکالی با فرجه زوج است. با توجه به خواص این نوع تابع، عبارت زیر رادیکال نمی‌تواند منفی باشد. بنابراین، داریم:

$$ x \ge ۰ $$

دامنه $$ \sqrt { x } $$ به صورت زیر نوشته می‌شود:

$$
D : \left\{ x | x \in \left [ ۰ , \ + \infty \right ) \right \}
$$

از آنجایی که $$ \sqrt { x } $$ در مخرج تابع کسری قرار دارد، عدد ۰ در دامنه $$ f ( x ) $$جای نخواهد داشت. برای نشان دادن این موضوع، علامت «$$ [ $$» را به «$$ ( $$» تغییر می‌دهیم:

$$
D _ { f ( x ) } : \left\{ x | x \in \left ( ۰ , \ + \infty \right ) \right \}
$$

یا

$$
D _ { f ( x ) } : \left\{ x | x \in R ^ + \right \}
$$

به عبارت دیگر، دامنه تابع کسری-رادیکالی $$ f ( x ) = \frac { ۱ } { \sqrt { x } } $$، اعداد حقیقی بزرگ‌تر از ۰ (اعداد حقیقی مثبت) را در برمی‌گیرد.

دامنه تابع رادیکالی چند جمله ای

«تابع چندجمله‌ای» (Polynomial Function)، به فرم زیر نوشته می‌شود:

$$
f ( x ) = a _ { n } x ^ { n } + \ a _ { n - ۱ } x ^ { n - ۱ } + \ ... \ + \ a _ { ۱ } x + \ a _ { ۰ }
$$

در بخش‌های قبلی، نحوه به دست آوردن دامنه توابع رادیکالی دارای تابع خطی (تابع چندجمله‌ای با $$ n = ۱ $$) را آموزش دادیم. در این بخش، روش‌های تعیین دامنه توابع رادیکالی چندجمله‌ای را مورد بررسی قرار می‌دهیم. برای شروع، چندجمله‌ای درجه دو زیر را در نظر بگیرید:

$$ f ( x ) = x ^ ۲ + x - ۱۲ $$

دامنه این تابع، مجموعه اعداد حقیقی است. به عبارت دیگر، با قرار دادن هر عدد دلخواه به عنوان ورودی درون این تابع، یک خروجی تعریف شده به دست می‌آید. بنابراین، دامنه تابع بالا عبارت است از:

$$ D : \{ x | x \in R \} $$

یا

$$ D : \{ x | x \in ( - \infty , \ + \infty ) \} $$

اکنون، تابع رادیکالی زیر را در نظر بگیرید:

$$ g ( x ) = \sqrt { x ^ ۲ + x - ۱۲ } $$

فرجه رادیکال در این تابع، زوج است. بنابراین، عبارت زیر رادیکال نمی‌تواند منفی باشد. از این‌رو، دامنه $$ g ( x ) $$، به مجموعه اعدادی محدود می‌شود که با قرار دادن آن‌ها در تابع، عبارت زیر رادیکال، برابر یا بزرگ‌تر از ۰ شود. به عبارت دیگر:

$$ x ^ ۲ + x - ۱۲ \ge ۰ $$

برای بررسی محدودیت بالا، ابتدا باید نقاط بحرانی $$ x ^ ۲ + x - ۱۲ $$ را پیدا کنیم. روش‌های مختلفی برای این کار وجود دارد. یکی از این روش‌ها، فاکتورگیری است. با فاکتورگیری از چندجمله‌ای، به عبارت زیر می‌رسیم:

$$
x ^ ۲ + x - ۱۲ = ( x + ۴ ) ( x - ۳ )
$$

بر این اساس، محدودیت دامنه را به شکل زیر بازنویسی می‌کنیم:

$$ ( x + ۴ ) ( x - ۳ )\ge ۰ $$

اگر $$ x $$ را برابر با ۳ یا ۴- قرار دهیم، خواهیم داشت:

$$
x = ۳ \implies ( x + ۴ ) ( ۳ - ۳ ) = ( x + ۴ ) ( ۰ ) = ۰
$$

$$
x = - ۴ \implies ( - ۴ + ۴ ) ( x - ۳ ) = ( ۰ ) ( x - ۳ ) = ۰
$$

بنابراین، ۳ و ۴-، نقاط بحرانی در تعیین دامنه هستند. این نقاط را بر روی محور اعداد مشخص می‌کنیم.

نقاط بحرانی دامنه تابع بر روی محور اعداد

توجه داشته باشید که به دلیل کسری نبودن تابع و قرار نداشتن عبارت رادیکالی در مخرج کسر، نقاط بحرانی با دایره‌های توپر مشخص می‌شوند. به عبارت دیگر، این نقاط نیز در دامنه تابع جای دارند. با در نظر داشتن نقاط بحرانی، محور اعداد را به سه ناحیه تقسیم می‌کنیم.

تقسیم بندی محور اعداد بر اساس نقاط بحرانی — تقسیم‌بندی محور اعداد بر اساس نقاط بحرانی

این نواحی عبارت هستند از:

محدوده اعداد بزرگ‌تر از ۳
محدوده اعداد بین ۴- تا ۳
محدوده اعداد کوچک‌تر از ۴-

برای بررسی مثبت یا منفی بودن عبارت زیر رادیکال در هر یک از نواحی بالا، یک عدد از آن‌ها را درون محدودیت دامنه قرار می‌‌دهیم. به عنوان مثال، عدد ۴ را در نظر بگیرید. با قرار دادن این عدد در محدوده دامنه تابع، خواهیم داشت:

$$
\begin{aligned} x = ۴ \implies ( ۴ + ۴ ) ( ۴ - ۳ ) \ge ۰ \\
( ۸ ) ( ۱ ) \ge ۰ \\
۸ \ge ۰ \\
\checkmark
\end{aligned}
$$

بنابراین، اعداد بزرگ‌تر از ۳، مثبت هستند و در بازه موجه دامنه قرار می‌گیرند.

محدوده موجه دامنه توابع رادیکالی چند جمله ای — تعیین اولین محدوده موجه دامنه

اکنون، عددی بین ۴- و ۳، مانند عدد ۰ را درون محدودیت دامنه قرار می‌دهیم:

$$
\begin{aligned} x = ۰ \implies ( ۰ + ۴ ) ( ۰ - ۳ ) \ge ۰ \\
( ۴ ) ( - ۳ ) \ge ۰ \\
- ۱۲ \ge ۰ \\
\times
\end{aligned}
$$

به این ترتیب، اعداد بین ۴- تا ۳، شرط قرارگیری در دامنه تابع را ارضا نمی‌کنند.

تعیین محدوده غیرموجه دامنه توابع رادیکالی چندجمله‌ای — تعیین محدوده غیرموجه دامنه تابع

برای محدوده سوم، عددی کوچک‌تر از ۴-، مانند -۵- را درون محدودیت دامنه تابع قرار می‌دهیم:

$$
\begin{aligned} x = - ۵ \implies ( - ۵ + ۴ ) ( - ۵ - ۳ ) \ge ۰ \\
( - ۱ ) ( - ۸ ) \ge ۰ \\
۸ \ge ۰ \\
\checkmark
\end{aligned}
$$

در آخرین مرحله، اعداد کوچک‌تر از ۴- نیز در مجموعه دامنه تابع جای خواهند داشت.

تعیین سومین محدوده موجه دامنه توابع رادیکالی چندجمله‌ای — تعیین سومین محدوده موجه دامنه تابع

در نتیجه، دامنه تابع $$ f ( x ) = x ^ ۲ + x - ۱۲ $$ به صورت زیر نوشته می‌شود:

$$
D : \{ x | x \in ( - \infty , \ - ۴ ] \cup [ ۳ , \ + \infty ) \}
$$

حل معادله درجه دو — به زبان ساده + فیلم آموزش رایگان

فیلم آموزش حسابان ۱ – پایه یازدهم – حل تمرین در فرادرس

مثال ۵: دامنه تابع رادیکالی با فرجه ۳

در این مثال قصد داریم دامنه تابع رادیکالی $$ f ( x ) = \frac { \sqrt [ ۳ ] { ۲ x ^ ۲ + ۳ } } { ۵ x - ۱ } $$ را تعیین کنیم. به این منظور، ابتدا فرجه رادیکال را مورد بررسی قرار می‌هیم. این فرجه برابر با ۳ است. به دلیل فرد بودن فرجه رادیکال، عبارت زیر آن می‌تواند هر عدد دلخواهی بین $$ - \infty $$ تا $$ + \infty $$ باشد.

با وجود عدم وجود محدودیت در مقدار ورودی عبارت رادیکالی، مخرج کسر دارای عبارتی با متغیر $$ x $$ است. بنابراین باید محدودیت صفر نشدن مخرج کسر را نیز در نظر بگیریم. بر اساس این محدودیت، داریم:

$$
\begin {aligned}۵ x - ۱ \ne ۰ \\
۵ x \ne ۱ \\
x \ne \frac { ۱ } { ۵ }
\end {aligned}
$$

به این ترتیب، $$ x $$ نمی‌تواند برابر با $$ \frac { ۱ } { ۵ } $$ باشد. در غیر اینصورت، مخرج کسر برابر با صفر شده و خروجی تابع، مقداری تعریف نشده می‌شد. در نتیجه، دامنه تابع $$ f ( x ) $$، مجموعه اعداد حقیقی ($$ - \infty $$ تا $$ + \infty $$) به جز $$ \frac { ۱ } { ۵ } $$ است:

$$
D : \{ x | x \in R , x \ne \frac { ۱ } { ۵ } \}
$$

یا

$$
D : \{ x | x \in ( - \infty , \ + \infty ) , x \ne \frac { ۱ } { ۵ } \}
$$

این دامنه بر روی محور اعداد، مشابه تصویر زیر نمایش داده می‌شود.

نمایش دامنه توابع رادیکالی کسری با فرجه سه در محور اعداد — نمایش دامنه تابع کسری رادیکالی با فرجه ۳ بر روی محور اعداد

دامنه توابع رادیکالی با قدر مطلق

«تابع قدر مطلق» (Absolute Value Function)، تابعی با خروجی غیرمنفی است. ساده‌ترین فرم این تابع به صورت زیر نوشته می‌شود:

$$ f ( x ) = | x | $$

فیلم آموزش ریاضی ۲ – پایه یازدهم علوم تجربی در فرادرس

در این تابع، داریم:

$$
f ( x ) = | x | = \begin{cases} x & \text{ if } x { \geq} ۰ \\ -x & \text { if } x < ۰ \end {cases}
$$

به زبان ساده‌تر، تابع قدر مطلق، مقادیر ورودی خود را به مقادیر غیرمنفی (۰ یا مثبت) تبدیل می‌کند. اکنون، ضمن به خاطر سپردن این ویژگی، تابع رادیکالی زیر را در نظر بگیرید:

$$ f ( x ) = \sqrt { | x | } $$

می‌خواهیم دامنه $$ f ( x ) $$ را به دست بیاوریم. به این منظور، ابتدا فرجه عبارت رادیکالی را بررسی می‌کنیم. به دلیل زوج بودن فرجه، عبارت زیر رادیکال باید بزرگ‌تر یا مساوی صفر شود. یعنی:

$$ | x | \ge ۰ $$

به جای $$ x $$، یک عدد مثبت نظیر ۱۰+ را قرار می‌دهیم و سازگاری آن با محدودیت بالا را بررسی می‌کنیم:

$$
x = +۱۰ \implies | + ۱۰ | = +۱۰
$$

$$
+۱۰ \ge ۰ \ \ \ \ \ \checkmark
$$

اکنون، به جای $$ x $$، یک عدد مثبت نظیر ۱۰- را قرار می‌دهیم و سازگاری آن با محدودیت بالا را بررسی می‌کنیم:

$$
x = -۱۰ \implies | - ۱۰ | = +۱۰
$$

$$
+۱۰ \ge ۰ \ \ \ \ \ \checkmark
$$

همان‌طور که مشاهده می‌کنید، به دلیل قرارگیری متغیر $$ x $$ در قدر مطلق، تمام خروجی‌های عبارت $$ | x | $$ و در نتیجه خروجی‌های تابع $$ f ( x ) = \sqrt { | x | } $$ غیرمنفی خواهد بود. به عبارت دیگر، دامنه این تابع، تمام اعضای مجموعه اعداد حقیقی است:

$$
D : \{ x | x \in ( - \infty , \ + \infty) \}
$$

یا

$$
D : \{ x | x \in R \}
$$

مثال ۶: تعیین دامنه تابع رادیکالی کسری با قدر مطلق

تابع زیر را در نظر بگیرید:

$$ f ( x ) = \frac { ۹ } { \sqrt [ ۴ ] { ۹ - | x + ۵ | } } $$

$$ f( x ) $$، یک تابع کسری و رادیکالی با فرجه زوج است. برای به دست آوردن دامنه این تابع باید دو محدودیت را در نظر بگیریم. محدودیت اول، منفی نشدن عبارت زیر رادیکال است. این محدودیت به صورت زیر نوشته می‌شود:

$$
\begin {aligned} ۹ - | x + ۵ | \ge ۰ \\
| x + ۵ | \le ۹ \\
- ۹ \le x + ۵ \le ۹ \\
-۱۴ \le x \le ۴
\end {aligned}
$$

بنابراین، $$ x $$ باید بین ۱۴- تا ۴ باشد تا علامت عبارت زیر رادیکال مثبت شود. با مشخص شدن این محدودیت، به سراغ محدودیت دوم می‌رویم. رادیکال، در مخرج کسر واقع شده است. بنابراین، عبارت زیر رادیکال نمی‌تواند برابر با ۰ باشد. یعنی:

$$
\begin {aligned} ۹ - | x + ۵ | \ne ۰ \\
| x + ۵ | \ne ۹
\end {aligned}
$$

$$
| x + ۵ | \ne ۹ \implies x + ۵ \ne ۹ \implies x \ne ۴ \\
$$

$$
| x + ۵ | \ne ۹ \implies x + ۵ \ne - ۹ \implies x \ne - ۱۴
$$

بنابراین، $$ x $$ نمی‌تواند دقیقا برابر با ۱۴- یا ۴ باشد. محدودیت‌های دامنه را در کنار یکدیگر می‌نویسیم:

$$
-۱۴ \le x \le ۴
$$

$$
x \ne ۴
$$

$$
x \ne - ۱۴
$$

بر اساس این محدودیت‌های می‌توانیم نتیجه بگیریم که $$ x $$، بین دو مقدار ۱۴- و ۴ قرار دارد:

$$
-۱۴ \lt x \lt ۴
$$

در نتیجه، دامنه تابع $$ f ( x ) $$ برابر است با:

$$
D : \{ x | x \in ( - ۱۴ , \ + ۴ ) \}
$$

دامنه توابع لگاریتمی رادیکالی

«تابع لگاریتمی» (Logarithmic Function)، تابعی است که عکس توابع توانی عمل می‌کند. تابع زیر، فرم ساده یک تابع لگاریتمی را نمایش می‌دهد:

$$ f ( x ) = \log _ { a } x $$

یا

$$ y = \log _ { a } x $$

رابطه بین پارامترهای نمایش داده شده در تابع بالا را می‌توان به صورت زیر بیان کرد:

$$ a ^ y = x $$

برخلاف توابع رادیکالی، کسری/گویا، چندجمله‌ای/توانی، توابع لگاریتمی در گروه توابع غیرجبری قرار می‌گیرند. دامنه توابع لگاریتمی، مطابق با جدول زیر است.

فرم تابع لگاریتمی	دامنه تابع لگاریتمی
$$ f ( x ) = \log _ a ( x ) $$	$$ ( ۰ , \ + \infty) $$
$$ f ( x ) = \log _ a ( m x \pm k ) $$	$$ ( \mp \frac { k } { m } , \ + \infty ) $$

همان‌طور که مشاهده می‌کنید، عبارت درون لگاریتم، همواره باید بزرگ‌تر از صفر باشد. بنابراین، محدودیت دامنه توابع لگاریتمی به صورت زیر نوشته می‌شود:

$$
f ( x ) = \log _ a ( x ) \implies x \gt ۰
$$

$$
f ( x ) = \log _ a ( m x \pm k ) \implies m x \pm k \gt ۰
$$

برای تعیین دامنه تابع لگاریتمی زیر رادیکال، محدودیت‌های توابع رادیکالی و لگاریتمی را در نظر می‌گیریم.

دامنه و برد توابع نمایی و لگاریتمی | به زبان ساده

فیلم آموزش حسابان ۱ – پایه یازدهم در فرادرس

مثال ۷: تعیین دامنه توابع لگاریتمی رادیکالی

توابع لگاریتمی زیر را در نظر بگیرید:

$$ f ( x ) = \log \left ( \sqrt { x } - ۴ \right ) $$

همان‌طور که مشاهده می‌کنید، داخل لگاریتم، یک عبارت رادیکالی وجود دارد. بنابراین، اگر بخواهیم دامنه $$ f ( x ) $$ را به دست بیاوریم، باید محدودیت‌های توابع لگاریتمی و رادیکالی را با هم مورد بررسی قرار دهیم. مبنای لگاریتم به صورت پیش‌فرض برابر با ۱۰ است. به منظور تعیین دامنه $$ f ( x ) $$، ابتدا محدودیت دامنه توابع لگاریتمی را می‌نویسیم:

$$
f ( x ) = \log _ a ( m x \pm k ) \implies m x \pm k \gt ۰
$$

بر اساس این محدودیت، داریم:

$$
\sqrt { x } - ۴ \gt ۰
$$

$$
\sqrt { x } \gt ۴
$$

$$ x \gt ۱۶ $$

بنابراین، متغیر $$ x $$ باید بزرگ‌تر از ۱۶ باشد. اکنون، به سراغ محدودیت دامنه توابع رادیکالی می‌رویم. فرجه رادیکال در $$ f ( x ) $$، زوج بوده و برابر با ۲ است. می‌دانیم که عبارت زیر رادیکال با فرجه زوج باید بزرگ‌تر مساوی ۰ باشد. از این‌رو:

$$ x \ge ۰ $$

در نتیجه، متغیر $$ x $$ باید بزرگ‌تر یا مساوی ۰ باشد. اکنون، این دو محدودیت را در کنار یکدیگر می‌نویسیم:

$$ x \ge ۰ $$

$$ x \gt ۱۶ $$

برای درک این محدودیت‌ها، بخشی از مجموعه اعداد درون آن‌ها را در نظر بگیرید:

$$
\{ ۰ ,\ ۱ , \ ۲ , \ ...,\ ۱۵, \ ۱۶, \ ۱۷, \ ۱۸ , \ ... , \ + \infty \}
$$

$$
\{ \ ۱۶, \ ۱۷, \ ۱۸ , \ ۱۹ , \ ۲۰ , \ ۲۱ ,\ ... , \ + \infty \}
$$

اشتراک بین این دو مجموعه، اعداد بزرگ‌تر از ۱۶ است. به این ترتیب، دامنه $$ f ( x ) $$ به صورت زیر نوشته می‌شود:

$$ D : \{ x | x \in ( ۱۶ , \ + \infty ) \} $$

دامنه توابع مثلثاتی زیر رادیکال

«توابع مثلثاتی» (Trigonometric Functions)، توابعی هستند که رابطه بین اضلاع و زوایای داخلی مثلث را نمایش می‌دهند.

فیلم آموزش حسابان ۱ – پایه یازدهم – حل تمرین در فرادرس

سینوس، کسینوس، تانژانت، کتانژانت، کسکانت و سکانت، شش تابع مثلثاتی اصلی به شمار می‌روند. جدول زیر، دامنه این توابع را نمایش می‌دهد.

تابع مثلثاتی	دامنه تابع مثلثاتی
$$ \sin ( x ) $$	$$ ( - \infty , \ + \infty ) $$
$$ \cos ( x ) $$	$$ ( - \infty , \ + \infty ) $$
$$ \tan( x ) $$	$$ R - ( ۲ n + ۱ ) \frac { \pi } { ۲ } $$
$$ \cot ( x ) $$	$$ R - n \pi $$
$$ \sec ( x ) $$	$$ R - ( ۲ n + ۱ ) \frac { \pi } { ۲ } $$
$$ \csc( x ) $$	$$ R - n \pi $$

در جدول بالا، $$ R $$، مجموعه اعداد حقیقی و $$ n $$، عضوی از مجموعه اعداد صحیح است. همان‌طور که مشاهده می‌کنید، دامنه توابع مثلثاتی مختلف با یکدیگر تفاوت دارد. به غیر از توابع سینوس و کسینوس، چهار تابع مثلثاتی دیگر دارای محدودیت دامنه هستند. اگر یک تابع مثلثاتی را زیر رادیکال ببریم، دامنه تابع رادیکالی بر اساس محدودیت رادیکال و محدودیت‌های نمایش داده شده در جدول بالا تعیین می‌شود. این مسئله را در ادامه و با حل یک مثال توضیح می‌دهیم.

مثال ۸: دامنه تابع رادیکال سینوس ایکس

در این مثال قصد داریم دامنه تابع $$ f ( x ) = \sqrt { \sin ( x ) } $$ را به دست بیاوریم. می‌دانیم که دامنه تابع $$ \sin ( x ) $$، مجموعه اعداد حقیقی است و هیچ محدودیتی برای مقدار ورودی این تابع مثلثاتی وجود ندارد. بنابراین، به سراغ محدودیت توابع رادیکالی، یعنی غیرمنفی بودن عبارت زیر رادیکال می‌رویم. برای $$ f ( x ) $$، این محدودیت به صورت زیر نوشته می‌شود:

$$ \sin ( x ) \ge ۰ $$

به عبارت دیگر، تابع سینوس باید بزرگتر یا مساوی ۰ باشد. علامت $$ \sin ( x ) $$، در ربع اول و دوم دایره مثلثاتی مثبت است. این دو ربع، از زاویه ۰ تا ۱۸۰ درجه یا همان $$ \pi $$ گسترش دارند.

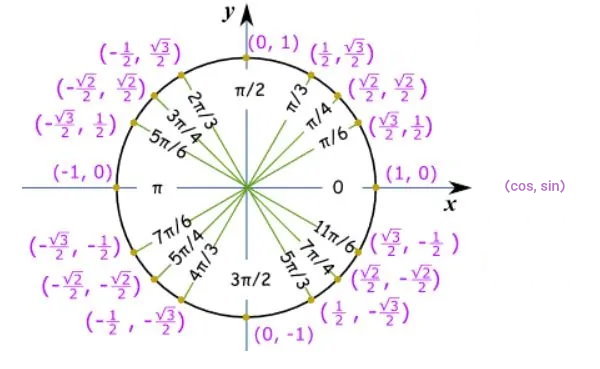
مقدار سینوس در زوایای ۰ و $$ \pi $$ برابر با ۰ است. از زاویه $$ \pi $$ تا $$ ۲ \pi $$ (ربع سوم و چهارم)، علامت سینوس منفی می‌شود. بنابراین، این زوایای در دامنه تابع مورد سوال قرار نخواهند داشت. دقت داشته باشید که زاویه $$ ۲ \pi $$، همان زاویه ۰ درجه است. به طور کلی، زوایای منطبق بر روی زاویه صفر با $$ ۲ n \pi $$ نمایش داده می‌شوند. نمایش زوایای منطبق بر روی زاویه ۱۸۰ درجه نیز با $$ ( ۲ n +۱ ) \pi $$ صورت می‌گیرد. در نتیجه، $$ \sin ( x ) $$، زمانی مثبت خواهد بود که از $$ ( ۲ n +۱ ) \pi $$ کوچک‌تر بوده و از $$ ۲ n \pi $$ بزرگ‌تر باشد. به این ترتیب، محدودیت دامنه برای تابع رادیکالی به صورت زیر نوشته می‌شود:

$$ ۲ n \pi \le x \le ( ۲ n + ۱ ) \pi $$

این محدودیت، همان دامنه تابع رادیکال سینوس ایکس است:

$$
D : \left\{ x | \ ۲ n \pi \le x \le ( ۲ n + ۱ ) \pi , \ n \in \mathbb{Z} ) \right \}
$$

دامنه توابع رادیکالی چند متغیره

«تابع چندمتغیره» (Multivariable Function)، تابعی است که بیش از یک متغیر مستقل دارد. به عنوان مثال، تابع $$ f ( x , \ y ) = xy $$، یک تابع چندمتغیره محسوب می‌شود.

فیلم آموزش حسابان ۱ – پایه یازدهم – حل تمرین در فرادرس

محدودیت دامنه توابع چندمتغیره، تفاوتی با توابع یک متغیره ندارد. به عنوان مثال، تابع زیر را در نظر بگیرید:

$$ f ( x , \ y ) = x ^ ۳ y + ۳ x ^ ۲ y ^ ۲ + y + ۱ $$

با وجود چندمتغیره بودن این تابع، فرم آن مطابق با توابع چندجمله‌ای است. بنابراین، دقیقا مانند توابع چندجمله‌ای، دامنه این تابع نیز محدودیتی ندارد و در بازه مجموعه اعداد حقیقی تعریف می‌شود. اگر این تابع را به زیر رادیکال با فرجه زوج ببریم، خوهیم داشت:

$$ f ( x , \ y ) = \sqrt { x ^ ۳ y + ۳ x ^ ۲ y ^ ۲ + y + ۱ } $$

می‌دانیم که عبارت زیر رادیکال با فرجه زوج نمی‌تواند منفی باشد. بنابراین، دامنه تابع رادیکالی چند متغیره بالا بر اساس این محدودیت به دست می‌آید. این محدودیت به صورت زیر نوشته می‌شود:

$$ x ^ ۳ y + ۳ x ^ ۲ y ^ ۲ + y + ۱ \ge ۰ $$

تعیین دامنه توابع رادیکالی چندمتغیره، فرآیند نسبتا پیچیده و وقت‌گیری دارد. در ادامه، یک مثال ساده از این دامنه را حل می‌کنیم.

مثال ۹: دامنه تابع چند متغیره زیر رادیکال

تابع زیر را در نظر بگیرید:

$$ f ( x , \ y ) \sqrt { ۹ - x ^ ۲ - ۹ y ^ ۲ } $$

$$ f ( x , \ y ) $$، یک تابع چندمتغیره رادیکالی با فرجه زوج است. برای به دست آوردن دامنه این تابع، از محدودیت دامنه توابع رادیکالی با فرجه زوج استفاده می‌کنیم. بر اساس این محدودیت، عبارت زیر رادیکال با فرجه زوج نباید کوچک‌تر از ۰ باشد. بنابراین:

$$ ۹ - x ^ ۲ - ۹ y ^ ۲ \ge ۰ $$

نامساوی بالا را بر حسب $$ x $$ و $$ y $$ بازنویسی می‌کنیم:

$$ x ^ ۲ + ۹ y ^ ۲ \le ۹ $$

$$ \frac { x } { ۹ } + y ^ ۲ \le ۱ $$

نامساوی بالا، شبیه به معادله بیضی است که به صورت زیر نوشته می‌شود:

$$ \frac { x ^ ۲ } { a ^ ۲ } + \frac { y ^ ۲ } { b ^ ۲ } = ۱ $$

$$ a $$ و $$ b $$، به ترتیب محور اصلی (قطر بزرگ) و محور فرعی (قطر کوچک) بیضی را نمایش می‌دهند.

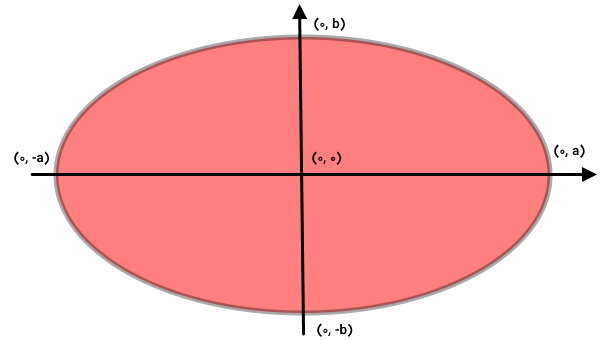
مختصات اجزای بیضی در دستگاه محورهای مختصات

نامعادله مربوط به محدودیت دامنه تابع مثال را با معادله بیضی مقایسه کنید:

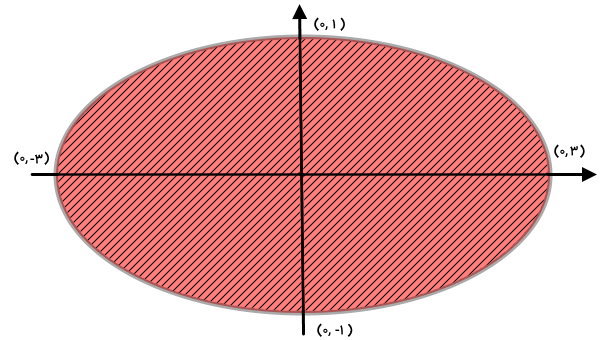
$$ \frac { x } { ۹ } + y ^ ۲ \le ۱ $$

$$ \frac { x ^ ۲ } { a ^ ۲ } + \frac { y ^ ۲ } { b ^ ۲ } = ۱ $$

بر اساس این روابط، قطر بزرگ برابر با ۳ و قطر کوچک برابر با ۱ است. بیضی و قطرهای بیضی را بر روی محورهای مختصات رسم می‌کنیم. با توجه به رابطه نامعادله، مقادیری که بر روی محیط بیضی و درون مساحت بیضی قرار دارند، به عنوان دامنه تابع $$ f ( x , \ y ) $$ محسوب می‌شوند.

حل تمرین دامنه توابع رادیکالی

در این بخش، به منظور آشنایی بیشتر و بهتر با نحوه به دست آوردن دامنه توابع رادیکالی، به حل چندین تمرین متنوع می‌پردازیم.

فیلم آموزش ریاضی ۲ – پایه یازدهم علوم تجربی در فرادرس

تمرین ۱: دامنه تابع خطی زیر رادیکال با فرجه زوج

دامنه تابع زیر را به دست بیاورید:

$$ f ( x ) = ۲ \sqrt [ ۶ ] { x + ۴ } $$

$$ f ( x ) $$، یک تابع رادیکالی با ۶ است. این تابع، یک تابع خطی را درون خود جای داده است. توابع خطی، هیچ محدودیتی در دامنه ندارند. به عبارت دیگر، دامنه توابع خطی برابر با مجموعه اعداد حقیقی ($$ \mathbb{R} $$) می‌شود. دامنه توابع رادیکالی نیز با توجه به فرد یا زوج بودن فرجه‌شان، یکی از گزینه‌های زیر است:

دامنه تابع رادیکالی با فرجه فرد: تمام اعداد حقیقی
دامنه تابع رادیکالی با فرجه زوج: اعداد حقیقی که عبارت زیر رادیکال را برابر یا بزرگ‌تر از ۰ کنند.

در این تمرین، فرجه رادیکال زوج (۶) است. بنابراین، عبارت زیر رادیکال باید برابر یا بزرگ‌تر از ۰ باشد:

$$ x + ۴ \ge ۰ $$

اگر نامساوی بالا را بر حسب x حل کنیم، به محدودیت زیر می‌رسیم:

$$ x \ge - ۴ $$

به عبارت دیگر، تنها با قرار دادن $$ x $$های بزرگ‌تر یا مساوی ۴- درون $$ f ( x ) $$، به جواب قابل قبول می‌رسیم. در نتیجه، دامنه تابع $$ f ( x ) $$ عبارت است از:

$$ D : \{ x | x \in [ - ۴ , \ + \infty ) \} $$

تمرین ۲: دامنه تابع رادیکالی در مخرج فرجه فرد

دامنه $$ f ( x ) = \sqrt [ ۳ ] { \frac { x + ۵ } { x ^ ۲ - ۳ x }} $$ را تعیین کنید.

$$ f ( x ) $$، یک تابع رادیکالی با فرجه فرد است که یک تابع گویا (تقسیم دو چندجمله‌ای) را درون خود جای می‌دهد. به منظور تعیین دامنه این تابع، باید محدودیت‌های توابع کسری و رادیکالی را در نظر بگیریم. برای شروع، به سراغ محدودیت دامنه توابع رادیکالی می‌رویم. به این منظور، فرجه رادیکال را بررسی می‌کنیم. این فرجه برابر با یک عدد فرد (۳) است. بنابراین، هیچ محدودیتی از نظر علامت زیر رادیکال نخواهیم داشت. به عبارت دیگر، محدوده قابل قبول برای دامنه رادیکال در اینجا، مجموعه اعداد حقیقی است.

در مرحله دوم، محدودیت دامنه توابع کسری را مورد بررسی قرار می‌دهیم. بر اساس این محدودیت، مخرج کسر نمی‌‌تواند برابر با ۰ باشد. بنابراین، داریم:

$$
x ^ ۲ - ۳ x \ne ۰
$$

از $$ x $$ در نامساوی بالا فاکتور می‌گیریم:

$$ x ( x - ۳ ) \ne ۰ $$

به این ترتیب:

$$ x \ne ۰ $$

$$ x - ۳ \ne ۰ $$

$$ x \ne ۳ $$

$$ x $$ به غیر از ۰ و ۳ می‌تواند هر عدد حقیقی دلخواهی باشد. در نتیجه، دامنه $$ f ( x ) $$ به صورت زیر نوشته می‌شود:

$$
D : \{ x | x \in R , \ x \ne \{ ۰, \ ۳ \} \}
$$

تمرین ۳: دامنه تابع رادیکالی در مخرج کسر

دامنه تابع زیر را به دست بیاورید:

$$ f ( x ) = \sqrt { \frac { ۴ }{ x + ۳ } } $$

$$ f ( x ) $$، یک تابع کسری رادیکالی است. برای به دست آوردن دامنه این نوع تابع، ابتدا محدودیت صفر شدن مخرج کسر را مورد بررسی قرار می‌دهیم. با توجه به این محدودیت، مخرج کسر (عبارت $$ x + ۳ $$) نباید برابر با صفر شود. بنابراین، داریم:

$$ x + ۳ \ne ۰ $$

$$ x \ne - ۳ $$

به این ترتیب، اولین محدودیت برای تعیین دامنه $$ f ( x ) $$ را به دست آوردیم. مطابق با این محدودیت، مقدار $$ x $$ نمی‌تواند برابر با عدد ۳- شود. اکنون به سراغ محدودیت‌های بعدی می‌رویم. فرجه عبارت رادیکالی در تابع $$ f ( x ) $$، زوج است. بنابراین، مقدار زیر رادیکال نباید منفی بوده اما می‌تواند برابر یا مساوی با صفر باشد. بنابراین، داریم:

$$
x + ۳ \ge ۰
$$

$$ x \ge - ۳ $$

به این ترتیب، محدودیت دوم برای تعیین دامنه $$ f ( x ) $$ را نیز به دست آوردیم. این دو محدودیت را در کنار یکدیگر می‌نویسیم:

$$ x \ne - ۳ $$

$$ x \ge - ۳ $$

اشتراک این دو محدودیت، $$ x \ne - ۳ $$ است. به عبارت دیگر، $$ x $$ فقط می‌تواند مقادیر بزرگ‌تر از ۳- را بگیرید. در نتیجه:

$$
D _ { f ( x ) } : \left\{ x | x \in \left ( - ۳ , \ + \infty \right ) \right \}
$$

تمرین ۴: دامنه تقسیم دو تابع رادیکالی

دامنه تابع زیر را به دست بیاورید:

$$ h ( x ) = \sqrt { \frac { ۲ x - ۸ }{ ۳ - x } } $$

تابع بالا، یک تابع کسری رادیکالی را نمایش می‌دهد. به منظور تعیین دامنه این تابع، ابتدا آن را به صورت زیر بازنویسی می‌کنیم:

$$
h ( x ) = \frac { \sqrt { ۲ x - ۸ } }{ \sqrt { ۳ - x } }
$$

اکنون یک تابع کسری داریم که صورت و مخرج آن، از توابع رادیکالی تشکیل می‌شود. برای شروع فرآیند تعیین دامنه، ابتدا محدودیت‌های مربوط به رادیکال‌ها را مشخص می‌کنیم. به دلیل زوج بودن فرجه رادیکال‌ها، عبارت‌های زیر آن‌ها باید بزرگ‌تر یا مساوی ۰ شود. برای رادیکال صورت کسر داریم:

$$
۲ x - ۸ \ge ۰
$$

$$ ۲ x \ge - ۸ $$

$$
x \ge \frac { - ۸ } { ۲ }
$$

$$
x \ge - ۴
$$

بر اساس این محدودیت، مقادیر $$ x $$ می‌توانند بزرگ‌تر یا مساوی ۴- باشند. به همین شکل، برای رادیکال مخرج کسر داریم:

$$
۳ - x \ge ۰
$$

$$
۳ \ge x
$$

بر اساس این محدودیت، مقادیر $$ x $$ می‌توانند کوچک‌تر یا مساوی ۳ باشند. برای درک بهتر این محدودیت‌ها، آن‌ها را بر روی محور اعداد رسم می‌کنیم.

نمایش دامنه‌ها بر روی محور اعداد — نمایش محدودیت‌های x بر روی محور اعداد

با توجه به نمایش گرافیکی محدودیت‌های بر روی محور اعداد می‌توانیم مشاهده کنیم که برای موجه بودن جواب هر دو رادیکال، مقدار $$ x $$ باید بزرگ‌تر یا مساوی ۳ باشد. این بازه، شرایط هر دو عبارت رادیکالی را ارضا می‌کند. نکته آخر در حل این تمرین، کسری بودن تابع مورد بررسی است. با توجه به این نکته، به سراغ محدودیت توابع کسری می‌رویم. در این توابع، مخرج کسر نمی‌تواند برابر با صفر باشد. بنابراین:

$$ \sqrt { ۳ - x } \ne ۰ $$

دو طرف را به توان ۲ می‌رسانیم:

$$
\left ( \sqrt { ۳ - x } \right ) ^ ۲ \ne ۰ ^ ۲
$$

$$
۳ - x \ne ۰
$$

$$ x \ne ۳ $$

به این ترتیب، عدد ۳ در دامنه تابع $$ h ( x ) $$ جای ندارد. اکنون، هر سه محدودیت به دست آمده را در کنار یکدیگر می‌نویسیم:

$$ x \ge - ۴ $$

$$ ۳ \ge x $$

$$ x \ne ۳ $$

بر اساس این محدودیت‌ها، نمایش دامنه بر روی محور اعداد به شکل زیر درمی‌آید.

حذف عدد ۳ از محور اعداد — حذف عدد ۳ از دامنه مجاز تابع

در نتیجه، دامنه $$ h ( x ) $$ به صورت زیر نوشته می‌شود:

$$
D : \left\{ x | x \in \left ( + ۳ , \ + \infty \right ) \right \}
$$

تمرین ۵: دامنه تابع گویا رادیکالی

دامنه تابع زیر را تعیین کنید:

$$ f ( x ) = \sqrt { \frac { ۶ - ۳ x }{ x - ۵ } } $$

تابع بالا، یک تابع گویا زیر رادیکال را نمایش می‌دهد. این تابع، ترکیبی از توابع کسری و رادیکالی است. بنابراین، تعیین دامنه آن بر اساس محدودیت‌های این توابع صورت می‌گیرد. برای حل تمرین، از محدودیت تابع کسری زیر رادیکال شروع می‌کنیم. در این تابع، مخرج کسر نباید برابر با ۰ باشد. از این‌رو، داریم:

$$ x - ۵ \ne ۰ $$

$$ x \ne ۵ $$

در نتیجه، متغیر $$ x $$ نباید برابر با ۵ باشد. بر اساس این محدودیت، عدد ۵ را از مجموعه اعداد دامنه خارج می‌کنیم.

نمایش عدد حذف شده از دامنه — نمایش قرار نداشتن عدد ۵ در دامنه با یک دایره توخالی در محور اعداد

اکنون، نوبت به محدودیت غیرمنفی بودن عبارت زیر رادیکال می‌رسد. این محدودیت به صورت زیر نوشته می‌شود:

$$ \sqrt { \frac { ۶ - ۳ x }{ x - ۵ } } \ge ۰ $$

نکته مهم در این تمرین، پیدا کردن مقدار غیرمنفی عبارت زیر رادیکال است. متغیر $$ x $$ هم در صورت و هم در مخرج کسر حضور دارد. اگر این متغیر را به گونه‌ای انتخاب کنیم که هم علامت صورت و هم علامت مخرج مثبت باشد، شرط بالا برقرار خواهد بود. این وضعیت در صورتی رخ می‌دهد که:

$$ ۶ - ۳ x \ge ۰ $$

$$ ۳ x \le ۶ $$

$$ x \le \frac { ۶ } { ۳ } $$

$$ x \le ۲ $$

$$ x - ۵ \gt ۰ $$

$$ x \gt ۵ $$

دقت داشته باشید که نمی‌توانیم برای مخرج، محدودیت مساوی را در نظر بگیریم. زیرا مخرج نباید ۰ شود. این محدودیت‌ها، هیچ اشتراکی با یکدیگر ندارند. برای درک این موضوع، آن‌ها را بر روی محور اعداد نمایش می‌دهیم.

عدم وجود اشتراک در محور اعداد — عدم وجود بازه مشترک محدودیت‌های دامنه در محور اعداد

فرآیند تعیین دامنه تابع، در این مرحله به پایان نمی‌رسد. حالت دیگری که در آن، علامت کسر مثبت می‌شود، منفی بودن علامت صورت و علامت مخرج است. این حالت زمانی رخ می‌دهد که:

$$ ۶ - ۳ x \le ۰ $$

$$ ۳ x \ge ۶ $$

$$ x \ge \frac { ۶ } { ۳ } $$

$$ x \ge ۲ $$

$$ x - ۵ \lt ۰ $$

$$ x \lt ۵ $$

این دو محدودیت، دارای بازه مشترک هستند. برای درک این بازه، محدودیت‌ها را بر روی محور اعداد پیاده می‌کنیم.

بازه مشتر دامنه توابع رادیکالی کسری — بازه مشترک محدودیت‌های دامنه (جواب موجه دامنه)

بر اساس محدودیت‌ها و نمایش آن‌ها در محور اعداد، دامنه تابع $$ f ( x ) $$ به صورت زیر نوشته می‌شود:

$$ D : \{ x | ۲ \le x \ ۵ \} $$

همان‌طور که مشاهده کردید، به منظور تعیین دامنه توابع، همیشه باید حالت‌های مختلف را به دقت بررسی کرد تا در صورت وجود جواب موجه، به آن دست یافت.

تمرین ۶: دامنه تابع لگاریتمی زیر رادیکال

دامنه تابع $$ f ( x ) = \sqrt { \log ( ۵ x - ۱ ) } $$ را تعیین کنید.

$$ f ( x ) $$، یک تابع رادیکالی با فرجه زوج است که در زیر رادیکال آن، یک تابع لگاریتمی بر مبنای ۱۰ قرار دارد. برای به دست آوردن دامنه این تابع، باید محدودیت‌های توابع لگاریتمی و رادیکالی را در نظر بگیریم. عبارت درون لگاریتم، همواره یک مقدار مثبت است. بنابراین، برای محدودیت اول، داریم:

$$ ۵x - ۱ \gt $$

$$ ۵ x \gt ۱ $$

$$ x \gt \frac { ۱ } { ۵ } $$

بر اساس محدودیت اول، متغیر $$ x $$ باید بزرگ‌تر از $$ \frac { ۱ } { ۵ } $$ باشد. از طرفی، عبارت زیر رادیکال باید بزرگ‌تر یا مساوی ۰ باشد. در نتیجه، برای محدود دوم، داریم:

$$
\log ( ۵ x - ۱ ) \ge ۰
$$

بر اساس قوانین لگاریتم، لگاریتم عدد ۱ همواره برابر با ۰ است. بنابراین:

$$
\log ( ۵ x - ۱ ) \ge \log ( ۱ )
$$

لگاریتم‌ها را از دو طرف نامساوی حذف می‌کنیم:

$$ ۵ x - ۱ \ge ۱ $$

$$ ۵ x \ge ۱ + ۱ $$

$$ ۵ x \ge ۲ $$

$$ x \ge \frac { ۲ } { ۵ } $$

بر اساس محدودیت دوم، متغیر $$ x $$ باید مساوی یا بزرگ‌تر از $$ \frac { ۲ } { ۵ } $$ باشد. هر دو محدودیت را در کنار یکدیگر می‌نویسیم:

$$ x \gt \frac { ۱ } { ۵ } $$

$$ x \ge \frac { ۲ } { ۵ } $$

اشتراک این دو محدودیت، مقادیر بزرگ‌تر مساوی $$ \frac { ۲ } { ۵ } $$ است. بنابراین، دامنه $$ f ( x ) $$ به صورت زیر نوشته می‌شود:

$$
D : \left\{ x | x \in \left [ \frac { ۲ } { ۵ } , \ + \infty \right ) \right \}
$$

تمرین ۷: دامنه تابع لگاریتمی رادیکالی کسری با مخرج قدر مطلق

دامنه تابع $$ f ( x ) = \ln \left ( \sqrt { \frac { ۱ }{ \left | x ^ ۲ - ۱ \right | } } \right ) $$ را به دست بیاورید.

برای تعیین دامنه تابع $$ f ( x ) $$، ابتدا محدودیت‌های آن را مورد بررسی قرار می‌دهیم. $$ f ( x ) $$، یک تابع لگاریتمی است که یک تابع رادیکالی را در خود جای داده است. در زیر رادیکال، یک تابع کسری و در مخرج کسر، یک عبارت چندجمله‌ای درون قدر مطلق وجود دارد.

می‌دانیم که توابع قدر مطلق و چندجمله‌ای، هیچ محدودیتی در دامنه خود ندارند. با این وجود، قدر مطلق چندجمله‌ای در مخرج یک کسر واقع شده است. بنابراین، خروجی آن نباید برابر با ۰ باشد. این محدودیت به صورت زیر نوشته می‌شود:

$$
\begin{aligned}
\left | x ^ ۲ - ۱ \right | \ne ۰ \\
x ^ ۲ - ۱ \ne ۰ \\
x ^ ۲ \ne ۱ \\
x \ne \pm ۱
\end {aligned}
$$

به این ترتیب، $$ x $$ نمی‌تواند برابر با ۱ یا ۱- باشد. عبارت کسری زیر رادیکال قرار دارد. از این‌رو، حاصل کسر نباید منفی باشد. این محدودیت به صورت زیر نوشته می‌شود:

$$
\frac { ۱ }{ \left | x ^ ۲ - ۱ \right | } \ge ۰
$$

از آنجایی که صورت کسر برابر با یک عدد مثبت (۱+) بوده و مخرج آن، یک تابع قدر مطلق (تابع غیرمنفی) است، علامت کسر همواره غیرمنفی خواهد بود. به عبارت دیگر، تمام مقادیر حقیقی در شرط بالا صدق می‌کنند. به همین دلیل، این شرط از فهرست محدودیت‌ها خارج می‌شود.

در آخرین مرحله، به سراغ محدودیت تابع لگاریتم طبیعی $$ \ln $$ می‌رویم. می‌دانیم که عبارت درون لگاریتم نباید ۰ یا کوچک‌تر از ۰ باشد. با توجه به این نکته، محدودیت سوم را می‌نویسیم:

$$
\sqrt { \frac { ۱ }{ \left | x ^ ۲ - ۱ \right | } } \gt ۰
$$

در هنگام بررسی محدودیت غیر منفی بودن عبارت زیر رادیکالی، دیدیم که $$ \frac { ۱ }{ \left | x ^ ۲ - ۱ \right | } $$، همواره غیر منفی است. علاوه بر این، به دلیل ثابت بودن صورت کسر، این عبارت نمی‌تواند برابر با صفر شود. بنابراین، تنها محدودیت مورد نیاز برای به دست آوردن دامنه تابع مورد سوال، محدودیت زیر است:

$$
x \ne \pm ۱
$$

بر این اساس، $$ f ( x ) $$ می‌تواند هر مقدار حقیقی را به غیر از ۱+ و ۱- به عنوان ورودی بگیرید. در نتیجه دامنه تابع به صورت زیر نوشته می‌شود:

$$
D : \{ x: x \in \mathbb{R} , \ x \ne \{ - ۱ , \ + ۱ \} \}
$$

$$
D : \{ x: x \in ( - \infty , \ - ۱ ) \cup ( - ۱ , \ + ۱ ) \cup ( + ۱ , \ + \infty)\}
$$

تمرین ۸: دامنه تابع رادیکال تانژانت

تفاوت دامنه تابع $$ f ( x ) = \sqrt { \tan ( x ) } $$ با $$ f ( x ) = \sqrt { \frac { ۱ } { \tan ( x ) } } $$ را تعیین کنید.

تابع $$ f ( x ) $$، تابع مثلثاتی تانژانت ایکس را زیر رادیکال نمایش می‌دهد. دامنه تابع tanx به صورت زیر نوشته می‌شود:

$$ R - ( ۲ n + ۱ ) \frac { \pi } { ۲ } $$

هنگامی که تانژانت را زیر رادیکال با فرجه زوج قرار می‌دهیم، دامنه آن به زوایایی محدود می‌شود که تانژانت آن‌ها برابر با ۰ یا بزرگ‌تر از ۰ (مثبت) است. بنابراین، برای محدودیت دامنه تابع $$ f ( x ) $$ داریم:

$$ \tan ( x ) \ge ۰ $$

$$ \tan ( x ) $$ در ربع‌های اول (زوایای ۰ تا ۹۰ درجه) و سوم (زوایای بین ۱۸۰ تا ۲۷۰ درجه) دایره مثلثاتی مثبت است. البته در زوایای ۰ درجه و ۱۸۰ درجه ($$ \pi $$)، مقدار این تابع برابر با ۰ می‌شود. در زوایای ۹۰ درجه ($$ \frac { \pi } { ۲ } $$) و ۲۷۰ درجه ($$ \frac { ۲ \pi } { ۳ } $$)، تانژانت جواب تعریف شده ندارد. در نتیجه دامنه $$ f ( x ) = \sqrt { \tan ( x ) } $$ عبارت است از:

$$ D _ { f ( x ) } : \left \{ x : x \in \left [ ۰ , \ \frac { \pi } { ۲ } \right ) + k n \right \} $$

$$ k $$، مجموعه اعداد حسابی است. اعداد دامنه بالا، همان محدوده ربع‌های اول و سوم دایره مثلثاتی را با رعایت مرز جواب‌های موجه نمایش می‌دهد. اکنون به سراغ تعیین دامنه تابع $$ g ( x ) $$ می‌رویم. این تابع عبارت است از:

$$ f ( x ) = \sqrt { \frac { ۱ } { \tan ( x ) } } $$

همان‌طور که مشاهده می‌کنید، در $$ g ( x ) $$، تابع تانژانت به مخرج کسر منتقل شده است. همین موضوع، باعث به وجود آمدن محدودیت صفر نبودن مخرج کسر می‌شود. برای به دست آوردن دامنه، این محدودیت را به صورت زیر می‌نویسیم:

$$ \tan ( x ) \ne ۰ $$

تانژانت تنها در زوایای ۰ و ۱۸۰ درجه برابر با صفر است. بنابراین، متغیر $$ x $$ در تابع بالا نمی‌تواند برابر با ۰ یا $$ \pi $$ باشد. از این‌رو می‌توانیم بگوییم:

$$ x \ne ۰ , \ x \ne \pi $$

یا به طور کلی:

$$ x \ne k \pi $$

علاوه بر محدودیت بالا، محدودیت غیرمنفی بودن عبارت زیر رادیکال بر دامنه تابع $$ g ( x ) $$ نیز اعمال می‌شود. در واقع، تنها تفاوت دامنه تابع $$ f ( x ) $$ با دامنه تابع $$ g ( x ) $$، محدودیت بالا است. اگر این محدودیت را به دامنه $$ f ( x ) $$ اضافه کنیم، به دامنه تابع $$ g ( x ) $$ می‌رسیم. این دامنه عبارت است از:

$$ D _ { g ( x ) } : \left \{ x : x \in \left ( ۰ , \ \frac { \pi } { ۲ } \right ) + k n \right \} $$

با مقایسه دامنه بالا با دامنه $$ f ( x ) $$ مشاهده می‌کنید که زاویه ۰ و ضرایب $$ \pi $$ در دامنه $$ g ( x ) $$ وجود ندارند.

برد تابع رادیکالی چیست و چگونه به دست می آید؟

«برد» (Range)، مجموعه‌ای از خروجی‌های قابل قبول و تعریف شده یک تابع است. تعریف برد، معمولا با یکی دیگر از مفاهیم مهم تابع، یعنی «هم‌دامنه» (Codomain) اشتباه گرفته می‌شود.

فیلم مجموعه آموزش دروس متوسطه دوم و کنکور – درس، تمرین، حل مثال و تست در فرادرس

برای درک مفهوم این دو، تعاریف زیر را با یکدیگر مقایسه کنید:

هم‌دامنه: خروجی‌های احتمالی
برد: خروجی‌های واقعی

هم‌دامنه می‌تواند برابر یا بزرگ‌تر از برد باشد. به عنوان مثال، تابع $$ f ( x ) = \sqrt { x } $$ را در نظر بگیرید. در بخش‌های قبلی آموختیم که دامنه این تابع رادیکالی، مجموعه اعداد غیرمنفی (۰ تا $$ + \infty $$) است. می‌دانیم خروجی یک رادیکال با فرجه زوج نمی‌تواند کوچک‌تر از صفر باشد. بنابراین، خروجی‌های احتمالی و قابل قبول برای این دامنه نیز مجموعه اعداد غیرمنفی خواهد بود.

اکنون، مجموعه زیر را به عنوان دامنه تابع $$ f ( x ) $$ در نظر بگیرید.

$$ \{ ۱, \ ۴, \ ۹, \ ۱۶, \ ۲۵\} $$

هم‌دامنه تابع، مجموعه اعداد غیرمنفی حقیقی است. به عبارت دیگر، مجموعه خروجی‌های احتمالی و قابل قبول، تحت تاثیر تغییر دامنه قرار نمی‌گیرد. اگر اعداد مجموعه بالا را درون تابع قرار دهیم، به مجموعه خروجی‌های زیر می‌رسیم:

$$ \{ ۱, \ ۲, \ ۳, \ ۴, \ ۵\} $$

به این مجموعه، برد تابع است. برد، به دامنه بستگی دارد و با تغییر آن تغییر می‌کند. اگر دامنه را برابر با مجموعه اعداد حقیقی غیرمنفی در نظر می‌گرفتیم، برد تابع نیز برابر با مجموعه اعداد حقیقی غیرمنفی شده و با هم‌دامنه برابری می‌کرد. در نتیجه، برد تابع رادیکالی، با قرار دادن ورودی‌های مجاز به درون تابع و به دست آوردن خروجی‌های مجاز به دست می‌آید.

سوالات متداول در رابطه با دامنه توابع رادیکالی

در این بخش، به برخی از پرتکرارترین سوالات مرتبط با دامنه انواع تابع رادیکالی به طور مختصر پاسخ می‌دهیم.