توابع نمایی و لگاریتمی در ریاضیات و سایر علوم کاربردهای فراوانی دارند و به همین دلیل است که شناخت این توابع ضروری است. در این آموزش، با دامنه و برد توابع نمایی و لگاریتمی آشنا میشویم و با ارائه مثالهایی نحوه تعیین دامنه و برد توابع نمایی و لگاریتمی را بیان میکنیم.
تعریف دامنه یک تابع
دامنه تابعی مانند f f f x x x اعداد حقیقی متغیر x x x
تعریف برد یک تابع
برد تابع f f f x x x
تعیین دامنه و برد توابع نمایی و لگاریتمی
برای به دست آوردن دامنه و برد یک تابع ابتدا باید نوع آن تابع را تشخیص دهیم، زیرا توابع گوناگون از جمله توابع جبری، لگاریتمی ، گویا، مثلثاتی و... دامنه و برد متفاوتی دارند. در ادامه این مطلب، به منظور آشنایی با نحوه تعیین دامنه و برد توابع نمایی و لگاریتمی مثالهایی را ارائه خواهیم کرد.
دامنه و برد تعدادی از توابع نمایی و لگاریتمی به شرح زیر است:
برد دامنه تابع ( 0 , + ∞ ) ( 0 , + ∞ ) ( 0 , + ∞ ) ( − ∞ , + ∞ ) ( - ∞ , + ∞ ) ( − ∞ , + ∞ ) f ( x ) = a x f ( x ) = a ^ x f ( x ) = a x ( ± k , + ∞ ) ( ± k , + ∞ ) ( ± k , + ∞ ) ( − ∞ , + ∞ ) ( - ∞ , + ∞ ) ( − ∞ , + ∞ ) (k k k f ( x ) = a x ± k f ( x ) = a ^ x ± k f ( x ) = a x ± k ( − ∞ , + ∞ ) ( - ∞ , + ∞ ) ( − ∞ , + ∞ ) ( 0 , + ∞ ) ( 0 , + ∞ ) ( 0 , + ∞ ) f ( x ) = log a ( x ) f ( x ) = \log _ a ( x ) f ( x ) = log a ( x ) ( − ∞ , + ∞ ) ( - ∞ , + ∞ ) ( − ∞ , + ∞ ) ( ∓ k m , + ∞ ) ( ∓ \frac k m , + ∞ ) ( ∓ m k , + ∞ ) (m m m k k k f ( x ) = log a ( m x ± k ) f ( x ) = \log_ a ( m x ± k ) f ( x ) = log a ( m x ± k )
نکته:
اگر log a x ≥ y \log_ a x ≥ y log a x ≥ y a > 1 a > 1 a > 1 x ≥ a y x ≥ a ^ y x ≥ a y
اگر log a x ≥ y \log _ a x ≥ y log a x ≥ y a < 1 a < 1 a < 1 x ≤ a y x ≤ a ^ y x ≤ a y
مثال های تعیین دامنه و برد توابع نمایی و لگاریتمی
در این بخش، چند مثال را از تعیین دامنه و برد توابع نمایی و لگاریتمی بیان میکنیم.
مثال اول دامنه و برد توابع نمایی و لگاریتمی
دامنه تابع f ( x ) = log 3 ( x − 1 ) f ( x ) = \log_3 ( x - 1 ) f ( x ) = log 3 ( x − 1 )
حل: طبق جدول فوق، اگر آرگومان log 3 ( x − 1 ) \log _ 3 ( x - 1 ) log 3 ( x − 1 ) x − 1 x - 1 x − 1 f ( x ) f ( x ) f ( x ) حقیقی خواهد بود:
x − 1 > 0 \large x - 1 > 0 x − 1 > 0
بنابراین، دامنه این تابع برابر است با x > 1 x > 1 x > 1 ( 1 , + ∞ ) ( 1 , + ∞ ) ( 1 , + ∞ )
مثال دوم دامنه و برد توابع نمایی و لگاریتمی
دامنه تابع f ( x ) = log 2 ( x 2 + 5 ) f ( x ) = \log _ 2 ( x ^ 2 + 5 ) f ( x ) = log 2 ( x 2 + 5 )
حل: آرگومان این تابع، یعنی x 2 + 5 x ^ 2 + 5 x 2 + 5 ( − ∞ , + ∞ ) ( - ∞ , + ∞ ) ( − ∞ , + ∞ )
مثال سوم دامنه و برد توابع نمایی و لگاریتمی
دامنه تابع f ( x ) = ln ( 9 − x 2 ) f ( x ) = \ln ( 9 - x ^ 2 ) f ( x ) = ln ( 9 − x 2 )
حل: برای اینکه ln ( 9 − x 2 ) \ln( 9 - x ^ 2 ) ln ( 9 − x 2 ) 9 − x 2 9 - x ^ 2 9 − x 2
9 − x 2 > 0 , x 2 < 9 , − 3 < x < 3 \large 9 - x ^ 2 > 0 , \\
\large x ^ 2 < 9 , \\
\large - 3 < x < 3 9 − x 2 > 0 , x 2 < 9 , − 3 < x < 3
مثال چهارم دامنه و برد توابع نمایی و لگاریتمی
دامنه تابع f ( x ) = log 4 ∣ x − 3 ∣ f ( x ) = \log _ 4 | x - 3 | f ( x ) = log 4 ∣ x − 3∣
حل: مانند مثالهای قبل، آرگومان تابع باید مثبت باشد، یعنی:
∣ x − 3 ∣ > 0 \large | x - 3 | > 0 ∣ x − 3∣ > 0
همانطور که میدانیم، خروجی قدر مطلق ، همواره یک مقدار مثبت است. بنابراین، دامنه این تابع برابر است با تمام اعداد حقیقی به جز 3 3 3
مثال پنجم دامنه و برد توابع نمایی و لگاریتمی
دامنه تابع f ( x ) = ln ( 2 x 2 − 3 x − 5 ) f ( x ) = \ln( 2 x ^ 2 - 3 x - 5 ) f ( x ) = ln ( 2 x 2 − 3 x − 5 )
حل: برای تعیین دامنه این تابع، باید نامعادله زیر را حل کنیم:
2 x 2 − 3 x − 5 > 0 \large 2 x ^ 2 - 3 x - 5 > 0 2 x 2 − 3 x − 5 > 0
با تجزیه عبارت سمت چپ به صورت زیر، میتوان مجموعه جواب نامعادله را به دست آورد:
( 2 x − 5 ) ( x + 1 ) > 0 \large ( 2 x - 5 ) ( x + 1 ) > 0 ( 2 x − 5 ) ( x + 1 ) > 0
اگر این نامساوی را تعیین علامت کنیم، خواهیم داشت:
( − ∞ , − 1 ) ∪ ( 5 2 , + ∞ ) \large ( - ∞ , - 1 ) \cup ( \frac 5 2 , + ∞ ) ( − ∞ , − 1 ) ∪ ( 2 5 , + ∞ )
مثال ششم دامنه و برد توابع نمایی و لگاریتمی
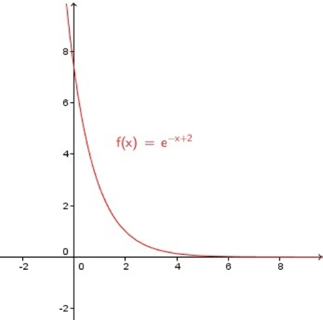
برد تابع f ( x ) = e − x + 2 f ( x ) = e ^ { - x + 2 } f ( x ) = e − x + 2
حل: ابتدا f ( x ) f ( x ) f ( x )
y = e − x + 2 \large y = e ^ { - x + 2 } y = e − x + 2
سپس، تابع را برای x x x
− x + 2 = ln ( y ) ⇒ x = 2 − ln ( y ) \large - x + 2 = \ln ( y ) \Rightarrow x = 2 - \ln ( y ) − x + 2 = ln ( y ) ⇒ x = 2 − ln ( y )
اگر y > 0 y > 0 y > 0 x x x ( 0 , + ∞ ) ( 0 , + ∞ ) ( 0 , + ∞ )
مثال هفتم دامنه و برد توابع نمایی و لگاریتمی
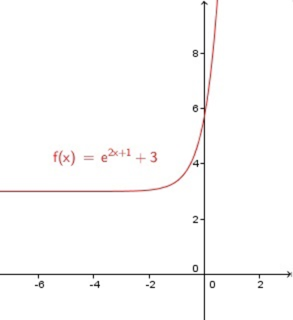
برد تابع f ( x ) = e 2 x + 1 + 3 f ( x ) = e ^ { 2 x + 1 } + 3 f ( x ) = e 2 x + 1 + 3
حل: مانند مثال قبل، تابع را برای x x x
y = e 2 x + 1 + 3 ⇒ y − 3 = e 2 x + 1 , 2 x + 1 = ln ( y − 3 ) , ⇒ 2 x = ln ( y − 3 ) − 1 x = 1 2 [ ln ( y − 3 ) − 1 ] \large y = e ^ { 2 x + 1 } + 3 \Rightarrow y - 3 = e ^ {2 x + 1 }, \\ \large 2 x + 1 = \ln ( y - 3 ) , \Rightarrow 2 x = \ln ( y - 3 ) - 1 \\ \large
\large x = \frac 1 2 [\ln ( y - 3 ) - 1 ] y = e 2 x + 1 + 3 ⇒ y − 3 = e 2 x + 1 , 2 x + 1 = ln ( y − 3 ) , ⇒ 2 x = ln ( y − 3 ) − 1 x = 2 1 [ ln ( y − 3 ) − 1 ]
مقدار x x x y − 3 > 0 y - 3 > 0 y − 3 > 0 ( 3 , + ∞ ) ( 3 , + ∞ ) ( 3 , + ∞ )
مثال هشتم دامنه و برد توابع نمایی و لگاریتمی
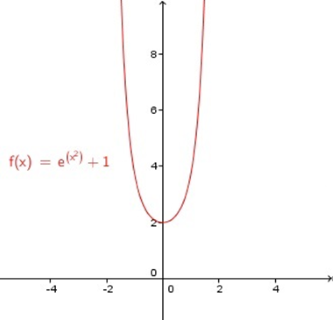
برد تابع f ( x ) = e x 2 + 1 f ( x ) = e ^ { x ^ 2 } + 1 f ( x ) = e x 2 + 1
حل: برای به دست آوردن برد این تابع نمایی به صورت زیر عمل میکنیم:
y = e x 2 + 1 ⇒ y − 1 = e x 2 , x 2 = ln ( y − 1 ) , x = ± ln ( y − 1 ) \large y = e ^ { x ^ 2 } + 1 \Rightarrow y - 1 = e ^ { x ^ 2 } , \\ \large x ^ 2 = \ln ( y - 1 ) , x=±\sqrt {\ln ( y - 1 ) } y = e x 2 + 1 ⇒ y − 1 = e x 2 , x 2 = ln ( y − 1 ) , x = ± ln ( y − 1 )
این جوابها در صورتی حقیقی هستند که
ln ( y − 1 ) ≥ 0 ⇒ ln ( y − 1 ) ≥ ln ( 1 ) , ⇒ y − 1 ≥ 1 ⇒ y ≥ 2 \large \ln ( y - 1 ) ≥ 0 \Rightarrow \ln ( y - 1 ) ≥ \ln ( 1 ) ,\\ \large \Rightarrow y - 1 ≥ 1 \Rightarrow y ≥ 2 ln ( y − 1 ) ≥ 0 ⇒ ln ( y − 1 ) ≥ ln ( 1 ) , ⇒ y − 1 ≥ 1 ⇒ y ≥ 2
مثال نهم دامنه و برد توابع نمایی و لگاریتمی
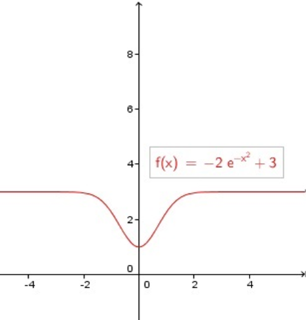
برد تابع f ( x ) = − 2 e − x 2 + 3 f ( x ) = - 2 e ^ {- x ^2 } + 3 f ( x ) = − 2 e − x 2 + 3
حل:
y = − 2 e − x 2 + 3 ⇒ y − 3 = − 2 e − x 2 , e − x 2 = y − 3 − 2 ⇒ − x 2 = ln y − 3 − 2 , x = ± − ln ( y − 3 − 2 ) \large y = - 2 e ^ { - x ^ 2 } + 3 \Rightarrow y - 3 = - 2 e ^ {-x ^ 2 } , \\ \large e ^ {- x ^2 } = \frac { y - 3 } { - 2 } \Rightarrow - x ^ 2 = \ln{ \frac { y - 3 }{ -2} }, \\
\large x = ± \sqrt { - \ln(\frac {y-3}{-2}) } y = − 2 e − x 2 + 3 ⇒ y − 3 = − 2 e − x 2 , e − x 2 = − 2 y − 3 ⇒ − x 2 = ln − 2 y − 3 , x = ± − ln ( − 2 y − 3 )
اگر آرگومان ln \ln ln x x x
y − 3 − 2 > 0 − ln ( y − 3 − 2 ) ≥ 0 \large \frac { y - 3 } { - 2 } >0 \\
\large - \ln(\frac { y - 3 }{-2} ) ≥ 0 − 2 y − 3 > 0 − ln ( − 2 y − 3 ) ≥ 0
مجموعه جواب نامعادله اول به صورت زیر است:
y − 3 − 2 > 0 ⇒ y − 3 < 0 ⇒ y < 3 \large \frac {y-3}{-2}>0 \Rightarrow y - 3 < 0 \Rightarrow y < 3 − 2 y − 3 > 0 ⇒ y − 3 < 0 ⇒ y < 3
و برای جواب معادله دوم، داریم:
− ln ( y − 3 − 2 ) ≥ 0 ⇒ ln ( y − 3 − 2 ) ≤ 0 , ln ( y − 3 − 2 ) ≤ ln ( 1 ) , ⇒ y − 3 − 2 ≤ 1 ⇒ y − 3 ≥ − 2 ⇒ y ≥ 1 \large - \ln(\frac {y-3}{-2 } ) ≥ 0 \Rightarrow \ln ( \frac { y - 3 } {-2} ) ≤ 0 , \\ \large \ln(\frac {y-3}{-2}) ≤ \ln ( 1 ) , \Rightarrow \frac {y-3} {-2}≤1 \Rightarrow y - 3 ≥ - 2 \Rightarrow y ≥ 1 − ln ( − 2 y − 3 ) ≥ 0 ⇒ ln ( − 2 y − 3 ) ≤ 0 , ln ( − 2 y − 3 ) ≤ ln ( 1 ) , ⇒ − 2 y − 3 ≤ 1 ⇒ y − 3 ≥ − 2 ⇒ y ≥ 1
بنابراین، برد تابع در بازه بسته [ 1 , 3 ) [ 1 , 3 ) [ 1 , 3 )
مثال دهم دامنه و برد توابع نمایی و لگاریتمی
دامنه تابع f ( x ) = log 10 6 x − x 2 8 f ( x ) = \sqrt { \log _ { 1 0 } \frac { 6 x - x ^ 2 } { 8 } } f ( x ) = log 10 8 6 x − x 2
حل: این تابع، جذر یک عبارت لگاریتمی است. از طرف دیگر، آرگومان تابع لگاریتمی نیز یک تابع گویا است. از این رو، برای تعیین دامنه این تابع، ابتدا مقادیری از x x x
6 x − x 2 8 > 0 ⇒ 6 x − x 2 > 0 \large \frac { 6 x - x ^ 2 } {8}>0 \Rightarrow 6 x - x ^ 2 > 0 8 6 x − x 2 > 0 ⇒ 6 x − x 2 > 0
طرفین نامعادله را در − 1 -1 − 1
x 2 − 6 x < 0 ⇒ x ( x − 6 ) < 0 \large x ^ 2 - 6x < 0 \Rightarrow x ( x - 6 ) < 0 x 2 − 6 x < 0 ⇒ x ( x − 6 ) < 0
ریشههای عبارت سمت چپ نامعادله، برابر است با x = 0 , 6 x=0,6 x = 0 , 6 x x x 0 0 0 6 6 6
اکنون شرط عبارت زیر رادیکال که باید مثبت یا صفر باشد را اعمال کنیم:
log 10 6 x − x 2 8 ≥ 0 ⇒ log 10 6 x − x 2 8 ≥ log 10 1 6 x − x 2 8 ≥ 1 ⇒ 6 x − x 2 − 8 ≥ 0 x 2 − 6 x + 8 ≤ 0 → ( x − 2 ) ( x − 4 ) ≤ 0 \large \log _ { 1 0 } { \frac { 6 x - x ^ 2 } { 8 } } ≥0\Rightarrow
\log_{10}{\frac {6x-x^2}{8}}≥\log_{10}1
\\ \large \frac { 6 x - x ^ 2 } { 8 } ≥ 1 \Rightarrow 6 x - x ^ 2 - 8 ≥ 0
\\ \large x ^ 2 - 6 x + 8 ≤ 0 → ( x - 2 ) ( x - 4 ) ≤ 0 log 10 8 6 x − x 2 ≥ 0 ⇒ log 10 8 6 x − x 2 ≥ log 10 1 8 6 x − x 2 ≥ 1 ⇒ 6 x − x 2 − 8 ≥ 0 x 2 − 6 x + 8 ≤ 0 → ( x − 2 ) ( x − 4 ) ≤ 0
واضح است که ریشههای عبارت سمت چپ نامعادله x = 2 , 4 x=2,4 x = 2 , 4
2 ≤ x ≤ 4 \large 2 ≤ x ≤ 4 2 ≤ x ≤ 4
برای تعیین دامنه تابع مفروض کافی است اشتراک بازههای به دست آمده برای x x x
دامنه f ( x ) f(x) f ( x ) [ 2 , 4 ] [2,4] [ 2 , 4 ]
مثال یازدهم دامنه و برد توابع نمایی و لگاریتمی
دامنه تابع f ( x ) = log 2 log 3 log 4 x f ( x ) = \log _ 2 \log _ 3 \log_ 4 x f ( x ) = log 2 log 3 log 4 x
حل: با توجه به اینکه این تابع شامل سه تابع لگاریتمی تودرتو با مبناهای مختلف است، ابتدا دامنه log 4 x \log_4x log 4 x x > 0 x>0 x > 0
برای حقیقی بودن عبارت log 3 log 4 x \log_3\log_4 x log 3 log 4 x
log 4 x > 0 \large \log_4 x > 0 log 4 x > 0
با توجه به اینکه مبنای لگاریتم بزرگتر از صفر است (به نکتهای که در ابتدای مطلب ذکر شده است، رجوع کنید)، داریم:
log 4 x > 0 ⇒ x > 4 0 ⇒ x > 1 \large \log _ 4 x > 0 \Rightarrow x > 4 ^ 0 \Rightarrow x > 1 log 4 x > 0 ⇒ x > 4 0 ⇒ x > 1
برای اینکه تابع f ( x ) f(x) f ( x ) log 3 log 4 x \log_ 3 \log _ 4 x log 3 log 4 x
log 3 ( log 4 x ) > 0 ⇒ log 4 x > 3 0 ⇒ log 4 x > 1 ⇒ x > 4 1 ⇒ x > 4 \large \log _ 3 (\log _ 4 x ) > 0 \Rightarrow \log_4 x > 3 ^{ 0 } \\ \large \Rightarrow \log_4x>1 \Rightarrow x>4^1 \Rightarrow x >
4 log 3 ( log 4 x ) > 0 ⇒ log 4 x > 3 0 ⇒ log 4 x > 1 ⇒ x > 4 1 ⇒ x > 4
با ترکیب این سه بازه و به دست آورد اشتراک آنها خواهیم داشت:
دامنه f ( x ) f(x) f ( x ) ( 4 , + ∞ ) ( 4 , + ∞ ) ( 4 , + ∞ )
مثال دوازدهم دامنه و برد توابع نمایی و لگاریتمی
برد تابع f ( x ) = log 10 ( x 2 − 3 x + 4 ) f ( x ) = \log _ {10} ( x ^ 2 - 3 x + 4 ) f ( x ) = log 10 ( x 2 − 3 x + 4 )
حل: آرگومان این تابع، یک تابع درجه دوم است، پس برای به دست آوردن برد تابع f ( x ) f(x) f ( x ) x x x مشتق اول و دوم آن را به دست آوریم:
d d x ( x 2 − 3 x + 4 ) = 2 x − 3 , d 2 d x 2 ( x 2 − 3 x + 4 ) = 2 \large \frac { d } { d x } ( x ^ 2 - 3 x + 4 ) = 2 x - 3 ,\\ \large \frac { d ^ 2 } { d x ^2 } ( x ^ 2 - 3 x + 4 ) = 2 d x d ( x 2 − 3 x + 4 ) = 2 x − 3 , d x 2 d 2 ( x 2 − 3 x + 4 ) = 2
با توجه به اینکه مشتق دوم بزرگتر از صفر است، x 2 − 3 x + 4 x ^ 2 - 3 x + 4 x 2 − 3 x + 4
2 x − 3 = 0 ⇒ x = 3 2 \large 2 x - 3 = 0 \Rightarrow x = \frac 3 2 2 x − 3 = 0 ⇒ x = 2 3
حال مقدار به دست آمده را در f ( x ) f(x) f ( x )
f ( 3 2 ) = log 10 ( ( 3 2 ) 2 − 3 ( 3 2 ) + 4 ) = log 10 ( 7 4 ) f ( x → ∞ ) → ∞ \large f ( \frac 32 ) = \log_{10} ( ( \frac 32 ) ^ 2 -3 ( \frac 32 ) + 4 ) = \log _ {10} ( \frac 7 4 ) \\ \large f ( x → ∞ ) → ∞
f ( 2 3 ) = log 10 (( 2 3 ) 2 − 3 ( 2 3 ) + 4 ) = log 10 ( 4 7 ) f ( x → ∞ ) → ∞
واضح است که برد تابع برابر است با [ log 10 ( 7 4 ) , + ∞ ) [\log_{10}(\frac 74) ,+ ∞) [ log 10 ( 4 7 ) , + ∞ )
مثال سیزدهم دامنه و برد توابع نمایی و لگاریتمی
دامنه تساوی e f ( x ) = e x − e e ^ { f ( x ) } = e ^ x - e e f ( x ) = e x − e
حل: برای به دست آوردن دامنه کافی است از دو طرف تساوی لگاریتم بر مبنای e e e
y = f ( x ) = log e ( e x − e ) → e x − e > 0 → e x > e → x > 1 \large y = f ( x ) = \log _ e ( e ^ x - e ) \\ \large
→ e ^ x - e > 0 → e ^ x > e → x > 1 y = f ( x ) = log e ( e x − e ) → e x − e > 0 → e x > e → x > 1
بنابراین، دامنه در بازه ( 1 , + ∞ ) ( 1 , + ∞ ) ( 1 , + ∞ )

















دمتون گرم عالی بود
Good
سلام.
سپاس از همراهیتان با مجله فرادرس.