تابع چیست؟ – در ریاضی و به زبان ساده + حل تمرین و مثال
تابع یکی از انواع رابطه است. در این نوع رابطه، اعضای دو مجموعه (مجموعه دامنه یا ورودی و مجموعه برد یا خروجی) به یکدیگر وصل میشوند. البته در توابع ریاضی، هیچ یک از اعضای ورودی، با بیش از یک عضو خروجی رابطه ندارد. به عبارت دیگر با قرار دادن یک ورودی در تابع، تنها به یک خروجی مشخص میرسیم. توابع ریاضی، انواع بسیار مختلفی دارند. در این مطلب از مجله فرادرس، ضمن پاسخگویی به پرسش تابع چیست، به مفاهیم مرتبط با توابع ریاضی نظیر برد، دامنه و همدامنه نیز میپردازیم. علاوه بر این، روشهای نمایش توابع و انواع تابع در ریاضی را نیز بیان میکنیم.
- یاد میگیرید ویژگیهای منحصربهفرد هر تابع را درک کنید.
- خواهید توانست فرق رابطه و تابع را تشخیص دهید.
- روشهای نمایش توابع را با مثال و فرمول خواهید آموخت.
- میآموزید که خروجی تابع را با ورودی مشخص حساب کنید.
- یاد خواهید گرفت ترکیب دو تابع را به دست آورید.
- انواع تابع و کاربرد هر کدام را خواهید شناخت.

تابع در ریاضی چیست؟
«تابع» (Function) یک مفهوم ریاضی است که رابطه بین دو مجموعه را نمایش میدهد. توابع ریاضی، پارامترهایی مانند عدد، حرف یا دیگر انواع ورودی را دریافت میکنند. سپس با انجام یکسری فرآیند بر روی پارامتر ورودی، یک خروجی مشخص را به دست میآورند. در مطالعه مبحث تابع در ریاضی، همواره به خاطر داشته باشید که هرگاه یک ورودی را درون تابع قرار دهید، قطعا به یک خروجی مشخص و ثابت میرسید. به عبارت دیگر، در یک تابع یک ورودی نمیتواند دو یا چند خروجی متفاوت داشته باشد.

توابع، از مهمترین مفاهیم در دنیای ریاضی و دنیای واقعی هستند. در ادامه، به منظور آشنایی بهتر با این مفهوم ریاضی، به ارائه چند مثال از تابع میپردازیم.
مثال تابع در دنیای واقعی
بسیاری از پدیدههایی که در دنیای واقعی رخ میدهند را میتوان در قالب توابع ریاضی بیان کرد. در واقع، هر سیستمی که با گرفتن یک یا چند ورودی، یک خروجی مشخص را ارائه کند، یک تابع در نظر گرفته میشود. به عنوان مثال، یک کارگر را در نظر بگیرید. اگر دستمزد ساعتی کارگر برابر با ۵۰ هزار تومان بوده و مجموع زمان فعالیت او در ماه برابر با ۱۸۰ ساعت باشد، حقوق ماهانه آن برابر با ۹ میلیون خواهد بود. در صورت افزایش ساعت کاری، حقوق ماهانه کارگر افزایش یافته و در صورت کاهش ساعت کاری، حقوق کارگر کاهش مییابد. به عبارت دیگر، حقوق ماهانه، تابعی از ساعت کاری است.

یکی دیگر از مثالهای تابع در دنیای واقعی، رابطه بین عرضه و تقاضا با قیمت یک محصول است. به طور کلی، اگر قیمت یک محصول افزایش پیدا کند، تقاضا برای آن کاهش یافته و عرضه آن افزایش مییابد. به عبارت دیگر، عرضه و تقاضا، تابعی از قیمت محصول هستند. از دیگر مثالهای تابع در دنیای واقعی میتوان به موارد زیر اشاره کرد:
- طول سایه اجسام تابعی از زمان است. به عنوان مثال، اجسام در ظهر، سایه بسیار کوچکی دارند.
- دمای یک محیط، تابعی از مکان و زمان است. به عنوان مثال، دمای مناطق کویری در فصل تابستان بیشتر از دمای نواحی کوهستانی در زمستان است.
- میزان سوخت مصرفی یک خودرو، تابعی از بهرهوری قطعات و طراحی است.
مثال تابع در دنیای هندسه
در دنیای هندسه، محاسبه بسیاری از اندازهها نظیر محیط و مساحت توسط توابع ریاضی انجام میگیرد. به عنوان مثال، محیط دایره با استفاده از فرمول زیر محاسبه میشود:
- : محیط دایره
- : عدد ثابت پی برابر
- : شعاع دایره
ضریب و عدد ، دو ثابت عددی در فرمول محیط دایره هستند. بنابراین، اندازه محیط دایره به اندازه شعاع آن بستگی دارد. به عبارت دیگر، محیط دایره، تابعی از شعاع است. بار دیگر به این نکته اشاره میکنیم که نه در دنیای واقعی و نه در دنیای ریاضی، هیچ تابعی نمیتواند با گرفتن یک ورودی ثابت، خروجیهای متفاوت داشته باشد. به عنوان مثال، هیچ آشپزی نمیتواند با استفاده از مواد اولیه سالاد شیرازی و رعایت دستور تهیه آن، کباب کوبیده درست کند.
تفاوت رابطه و تابع در ریاضی چیست؟
«رابطه» (Relation)، مجموعهای از جفتهای مرتب است. تابع در ریاضی، معمولا بر اساس مفهوم رابطه تعریف میشود. به عنوان مثال، مجموعه جفت اعداد زیر را در نظر بگیرید:
مجموعه بالا، یک رابطه است. به اولین مولفه در هر جفت از این مجموعه، «دامنه» (Domain) میگویند. مولفههای دوم هر جفت نیز با عنوان «برد» (Range) شناخته میشوند. بنابراین، دامنه و برد مجموعه بالا به ترتیب عبارت هستند از:
= دامنه
= برد
به هر یک از مولفههای دامنه، «مقدار ورودی» یا «متغیر مستقل» (Independent Variable) نیز میگویند. مقادیر ورودی را معمولا به حرف x نمایش میدهند. از طرف دیگر، مولفههای برد نیز با عناوینی نظیر «مقدار خروجی» یا «متغیر وابسته» (Dependent Variable) شناخته میشوند. این مقادیر را اغلب با حرف y نمایش میدهند.
تابع، رابطهای است که یک مقدار از برد را به مقادیر موجود در دامنه اختصاص میدهد. به عبارت «یک» در تعریف تابع دقت زیادی داشته باشید. منظور از این عبارت این است که هیچ یک از مقادیر x در تابع تکرار نمیشوند. به عنوان مثال، رابطه معرفی شده در ابتدای این بخش را دوباره در نظر بگیرید:
در این رابطه، اعداد موجود در برد (مولفههای دوم)، دو برابر اعداد موجود در دامنه (مولفههای اول) هستند. از آنجایی که هر یک از مولفههای برد () دقیقا با یکی از مولفههای دامنه () ارتباط دارد، رابطه بین آنها به عنوان یک تابع در نظر گرفته میشود. اکنون، رابطه زیر را در نظر بگیرید:
در رابطه بالا، هر یک از مولفههای دامنه (عبارتهای odd یا even)، تنها با یک مولفه از برد جفت نمیشود. به عنوان مثال، عبارت odd، با سه مقدار از برد () و عبارت even، با دو مقدار از برد () رابطه دارد. به این ترتیب، رابطه بالا نمیتواند یک تابع باشد. برای تعیین تابع بودن یا نبودن یک رابطه، سه مرحله زیر را انجام دهید:
- مقادیر ورودی را مشخص کنید.
- مقادیر خروجی را مشخص کنید.
- اگر هر مقدار ورودی، تنها به یک مقدار خروجی منتهی شود، رابطه در گروه تابع قرار میگیرد. در صورت به دست آمدن دو یا چند خروجی از یک ورودی، نمیتوان رابطه را به عنوان تابع در نظر گرفت.
مثال ۱
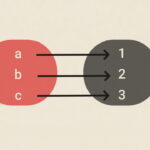
بر اساس تعریف تابع، کدامیک از این روابط موجود در تصویر زیر، یک تابع را نمایش میدهند؟

پاسخ
همانطور که مشاهده میکنید، رابطه بین مقادیر ورودی (دامنه) و خروجی (برد) در هر رابطه، با یک فلش نمایش داده شده است. بر اساس تعریف، اگر هر یک از مقادیر دامنه، تنها به یکی از مقادیر برد ارتباط داشته باشد، رابطه مورد نظر، یک تابع خواهد بود. در رابطه سمت راست، حروف m و n در برد، تنها به یکی از حروف q ،p یا r در دامنه ارتباط دارند. بنابراین، این رابطه، یک تابع را نمایش میدهد.
در رابطه میانی، حرف x در برد، تنها با حرف p در ورودی ارتباط دارد. با این وجود، حروف y و z در برد، هر دو به حرف q در دامنه وصل میشوند. از اینرو نمیتوان این رابطه را به عنوان تابع در نظر گرفت. در رابطه سمت چپ، حروف y ،x و z در برد، به ترتیب و به تنهایی با حروف q ،p و r در دامنه ارتباط دارند. در نتیجه، این رابطه نیز مانند رابطه سمت راست، یک تابع است.
مثال ۲
تصویر زیر، منوی یک کافیشاپ را نمایش میدهد. در ستون سمت راست، عنوان نوشیدنیها و ستون سمت چپ، قیمت هر نوشیدنی آورده شده است.

با توجه به منوی بالا، به سوالات زیر پاسخ دهید:
- آیا قیمت هر نوشیدنی، تابعی از نوع آن است؟
- آیا هر نوشیدنی، تابعی از قیمت آن است؟
پاسخ
برای پاسخ دادن به سوال اول، باید نوشیدنیها را به عنوان مقادیر ورودی و قیمت آنها را به عنوان مقادیر خروجی در نظر بگیریم. به این منظور، از عنوان هر نوشیدنی، یک فلش به سمت قیمت آن میکشیم.
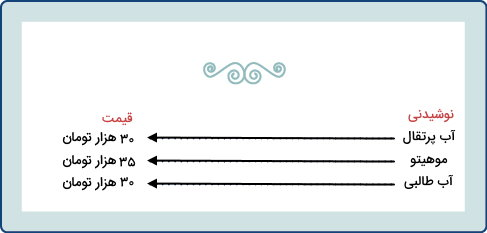
همانطور که مشاهده میکنید، هر نوشیدنی، تنها یک قیمت دارد. بنابراین، قیمت نوشیدنی، تابعی از نوع آن است. به عبارت دیگر، در صورت سفارش آب پرتقال، قطعا هزینه نوشیدنی ۳۰ هزار تومان میشود. اکنون، به سراغ پاسخ دادن به سوال دوم میرویم. برای این کار، قیمتها را به عنوان مقادیر ورودی و نوشیدنیها را به عنوان مقادیر خروجی در نظر میگیرم. سپس، قیمتهای مشابه را ادغام کرده و هر یک از آنها را توسط فلش به نوشیدنی مربوطه وصل میکنیم.
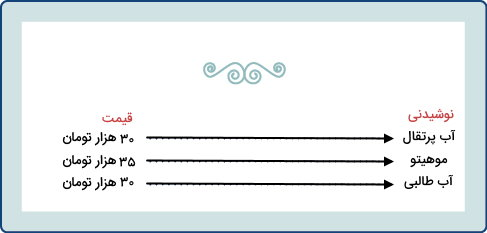
همانطور که مشاهده میکنید، یکی از قیمتها به دو نوشیدنی وصل میشود. در نتیجه، نوشیدنیها تابعی از قیمتشان نیستند. به عبارت دیگر، در صورت تمایل به انتخاب یک نوشیدنی ۳۰ هزار تومانی، دو گزینه (آب پرتقال یا آب طالبی) به عنوان خروجی ظاهر میشوند. شما میتوانید مباحث مرتبط با تابع و دیگر مباحث مهم در دروس ریاضی دانشگاه را با استفاده از مجموعه آموزش ریاضی پایه دانشگاهی فرادرس، به راحتی و به سرعت یاد بگیرید.
نمایش تابع در ریاضی
پس از مشخص شدن تابع بودن یک رابطه، نوبت به نمایش آن به زبان ریاضی میرسد. زمانی میتوان از یک تابع به بهترین شکل ممکن استفاده کنیم که قادر به نوشتن یا نمایش آن باشیم. تابع در ریاضی، معمولا با حرف f (ابتدای عبارت Function) نمایش داده میشود.
در برخی از موارد، حروفی مانند g و h نیز برای نشان دادن تابع مورد استفاده قرار میگیرند.
g ،f یا h، نام تابع و x، ورودی تابع است. توابع g(x) ،f(x) یا h(x)، با گرفتن مقدار ورودی x، خروجی منحصر به فردی نظیر y را نمایش میدهد. در اغلب منابع، توابع ریاضی به صورت زیر نوشته میشوند:
برای درک بهتر اصول نمایش تابع در ریاضی، رابطه بین سن و قد انسانها را در نظر بگیرید. قد یک فرد، تابعی از سن او است. اگر قد را با حرف h و سن را با a نمایش دهیم، تابع معرف رابطه بین قد و سن به صورت زیر خواهد بود:
به این ترتیب میگوییم؛ h تابعی از a است. a، به عنوان ورودی تابع، درون پرانتز قرار میگیرد. به خاطر داشته باشید که برای نامگذاری تابع میتوانیم از هر حرف دلخواهی استفاده کنیم. به عنوان مثال، میتواند به عنوان تابع بیانگر رابطه قد (h) و سن (a) باشد. در برخی از مواقع، ورودی تابع (پارامتر داخل پرانتز) به صورت یک عبارت جبری نوشته میشود. به عنوان مثال، تابع زیر را در نظر بگیرید:
این تابع، حاصل جمع دو متغیر a و b را به عنوان ورودی دریافت میکند و خروجی را مطابق با این حاصل جمع به دست میآورد. به طور کلی، چهار روش برای نمایش تابع در ریاضی وجود دارد. توابع ریاضی، معمولا به یکی از روشهای جبری، عددی، گرافیکی و یا توصیفی نمایش داده میشوند. در ادامه، هر یک از این روشها را مورد بررسی قرار خواهیم داد.
مثال ۱
از مفهوم تابع برای نوشتن تابعی با مشخصات زیر استفاده کنید:
- ورودی: نام ماه
- خروجی: تعداد روزهای ماه
پاسخ
تعداد روزهای یک ماه، تابعی از نام آن ماه است. بنابراین، داریم:
(ماه)f = تعداد روزهای ماه
اگر تعداد روزهای ماه را با حرف d (ابتدای عبارت Days) و ماه را با حرف m (ابتدای عبارت Month) مشخص کنیم، فرم تابع مورد نظر ما به شکل زیر درمیآید:
تابع f(m)، با گرفتن مقدار m (نام ماه)، مقدار d (تعداد روزهای ماه) را به ما میدهد. به عنوان مثال، اگر m برابر با اردیبهشت باشد، d برابر با ۳۱ خواهد بود:
۳۱ = (اردیبهشت)f
به همین ترتیب، برای ماه آبان داریم:
۳۰ = (آبان)f
ورودی تابع حتما نباید عدد باشد. ورودی یک تابع میتواند نام یا هر المان دیگری باشد که منجر به یک خروجی منحصر به فرد میشود. با این وجود، در اغلب موارد، با توابع دارای ورودی و خروجی عددی سر و کار داریم.
مثال ۲
تابع را در نظر بگیرید. اگر N تعداد پلیسهای شاغل در یک شهر بوده و y معرف سال باشد، مفهوم چیست؟
پاسخ
با توجه به اطلاعات مسئله، عدد داخل پرانتز (۱۴۰۰)، ورودی تابع (سال) و عدد دیگر (۳۰۰)، خروجی تابع (تعداد پلیسها) را نمایش میدهد. به ما نشان میدهد که در سال ۱۴۰۰، ۲۵۰ پلیس در شهر مشغول به کار بودهاند.
نمایش جبری تابع و تعیین فرمول تابع
منظور از نمایش جبری تابع، معادله یا مدل ریاضی معرف آن است. نوشتن مسائل دنیای واقعی در قالب یک تابع، مدلسازی ریاضی میگویند. یک تابع به همراه تمام متغیرهای ورودی، متغیرهای خروجی و یکای اندازهگیری، به عنوان مدل ریاضی شناخته میشوند. دیاگرام زیر، ورودی و خروجی یک تابع را با استفاده از عبارتهای جبری نشان میدهد:
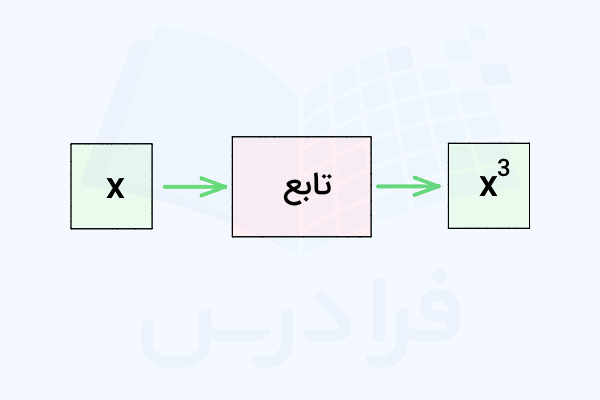
فرمول جبری تابع بالا به صورت زیر نوشته میشود:
یا
بر اساس فرمول بالا، با قرار دادن مقدار x به عنوان پارامتر ورودی در تابع f، خروجی به دست میآید. به عنوان مثال، برای ورودی با مقدار ، داریم:
عبارتهای جبری، سادهترین و قابل درکترین ابزارهای مورد استفاده برای نمایش تابع در ریاضی هستند. البته، به دست آوردن فرمول برخی از توابع، ساده نیست و دشواریهای مخصوص به خود را دارد. برای نمایش این توابع، از روشهای دیگر استفاده میشود.
مثال
یک دونده، در هر دقیقه، مسافت ۳۰۰ متر را طی میکند. میزان مسافت طی شده توسط این دونده را در قالب یک تابع جبری نمایش دهید. در مدت زمان ۵ دقیقه، دونده چه مسافتی را طی میکند؟
پاسخ
مسافت طی شده توسط دونده، تابع از زمان است. اگر زمان را با متغیری نظیر t نمایش دهیم، مسافت طی شده برابر با f(t) خواهد بود. بر اساس صورت سوال، میدانیم که در هر دقیقه (به ازای هر t)، ۳۰۰ متر توسط دونده طی میشود. به زبان ریاضی:
اگر زمان را به ۲ دقیقه افزایش دهیم، خواهیم داشت:
با توجه به فرمول و مقادیر محاسبه شده، فرمول تابع f(t) را به صورت زیر مینویسیم:
بنابراین، در مدت زمان ۵ دقیقه، دونده مسافت f(۵) را طی میکند:
در نتیجه، مسافت طی شده توسط دونده در مدت ۵ دقیقه برابر با ۱۵۰۰ متر است. در این مثال، نمایش جبری تابع، ساده بود. با این وجود، در برخی از مسائل، این کار به سادگی انجام نمیشود.
رسم نمودار تابع
یکی از روشهای متداول برای نمایش توابع ریاضی، رسم نمودار آنها است. در این روش، معمولا از دستگاه مختصات دوبعدی با محور افقی x و محور عمودی y استفاده میشود. به عنوان مثال، تصویر زیر را در نظر بگیرید. این تصویر، نمودار تابع f را نمایش میدهد:
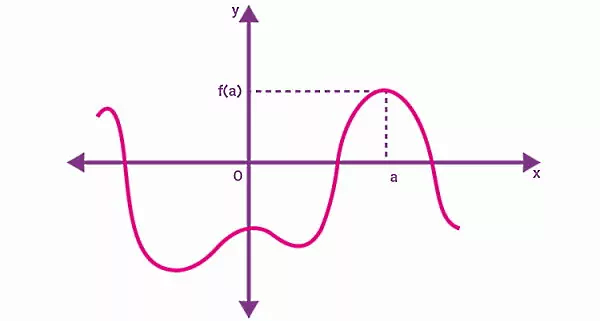
برای هر مقدار ورودی x، خروجی تابع f برابر با فاصله عمودی نمودار تا محور افقی x است. به عنوان مثال، در نمودار بالا، فاصله عمودی نمودار تابع تا محور x در نقطه برابر با است. منحنی یا نمودار تابع ، مجموعهای از نقاط دارای مختصات یا است که در دستگاه مختصات دوبعدی (دستگاه مختصات محورهای x و y) به نمایش درآمده میآید. تابع زیر را در نظر بگیرید:
تصویر زیر، نمودار تابع f(x) را نمایش میدهد:
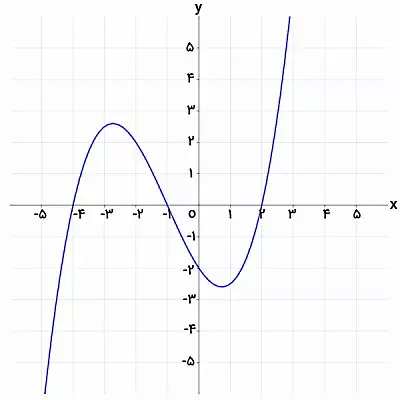
هر نقطه از نمودار بالا، دارای مختصات است. اگر تعداد کافی از ورودیها و خروجیهای f(x) را بر روی دستگاه مختصات مشخص کرده و آنها را به یکدیگر وصل کنیم، نمودار آن به وجود میآید. رسم تابع، امکان تخمین یا تعیین دقیق فرمول آن را توسط روشهایی نظر برازش منحنی فراهم میکند. نمودار توابع معروف، ساختار مشخصی دارد. به عنوان مثال، نمودار توابع چندجملهای درجه دو، به شکل یا با تقارن محوری است.

مقدار ماکزیمم یا مینیمم تابع درجه دو در رخ میدهد. به عبارت دیگر، برای به دست آوردن راس نمودار تابع درجه دو، باید مشتق آن را برابر با صفر قرار دهیم.
مثال
نمودار تابع را رسم کنید.
پاسخ
برای رسم نمودار یک تابع از روی فرمول جبری، باید مختصات چند نقطه از آن را به دست بیاوریم. تابع ، یک تابع درجه دو با شکل یا است. راس نمودار این تابع، اهمیت زیادی در رسم آن دارد. مختصات راس تابع درجه ۲، طی مشتقگیری از f(x) و برابر قرار دادن آن با ۰ تعیین میشود. به این ترتیب، داریم:
بنابراین، راس تابع در رخ میدهد. برای به دست آوردن اندازه y در این نقطه، را درون f(x) قرار میدهیم:
بنابراین، مختصات راس f(x) برابر با است. به همین ترتیب، مختصات ۴ نقطه دیگر را به دست میآوریم. برای سادگی، از جدول زیر استفاده میکنیم.
| مقدار x | مقدار y |
با مشخص کردن نقاط به دست آمده از جدول بالا بر روی دستگاه مختصات و اتصال آنها به یکدیگر، نمودار تابع رسم میشود:
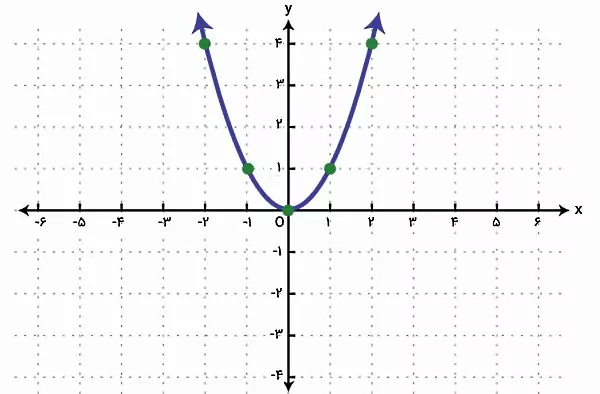
در صورت تمایل به آشنایی بیشتر با نحوه رسم نمودار توابع، مطالعه مطالب زیر از مجله فرادرس را به شما پیشنهاد میکنیم:
نمایش عددی تابع و ایجاد جدول
یکی دیگر از روشهای نمایش تابع، استفاده از جدول است. در جدول تابع، یکی از سطرها یا ستونها، معرف مقادیر ورودی (متغیر مستقل) بوده و دیگر سطر یا ستون، بیانگر مقادیر خروجی (متغیر وابسته) است. به عنوان مثال، تابع زیر را در نظر بگیرید:
مقادیر ورودی و خروجی تابع g(n) در جدول زیر آورده شدهاند.
| n (ورودی تابع) | Q (خروجی تابع) |
با وجود مشخص بودن مقادیر دقیق خروجیها در جدول تابع، تعداد خروجیها محدود است. این محدودیت، تحلیل تابع و مطالعه رفتار آن را دشوار میکند.
نمایش تابع به صورت توصیفی
چهارمین روش برای نمایش یک تابع، توصیف عملکرد آن است. به عنوان مثال، تابعی را در نظر بگیرید که به با گرفتن ورودی x، مقدار خروجی آن برابر با x شود. این عملکرد، یک تابع همانی را توصیف میکند. نمایش جبری تابع همانی به صورت زیر است:
نمایش تابع بالا در یک جدول به صورت زیر انجام میگیرد.
| x | f(x) |
:اگر بخواهیم شکل تابع توصیف شده را بر روی دستگاه مختصات پیاده کنیم، به نمودار زیر میرسیم
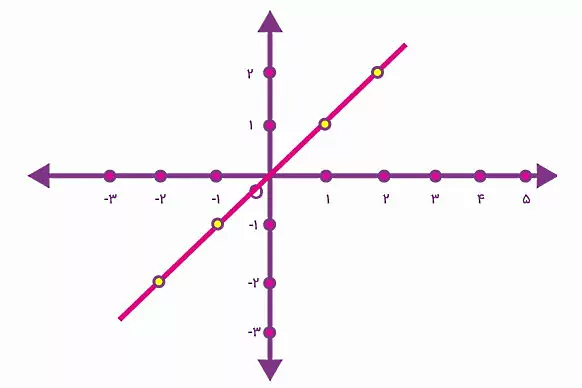
اکنون، تابعی را در نظر بگیرد که با قرار دادن ورودی x در آن، مقدار خروجی، یک عدد صحیح کوچکتر یا مساوی با x شود. این عملکرد، توصیف یک تابع جز صحیح است. توابع جز صحیح به صورت زیر نمایش داده میشوند:
مقادیر ورودی و خروجی زیر را میتوان به عنوان نمایش جدولی یک تابع جز صحیح در نظر گرفت.
| x | f(x) |
| ۱/۵- | |
| ۱- | |
| ۰/۵- | |
| ۰/۵ | |
| ۱ | |
| ۱/۵ |
نمودار زیر، نمایش گرافیکی تابع جز صحیح است:
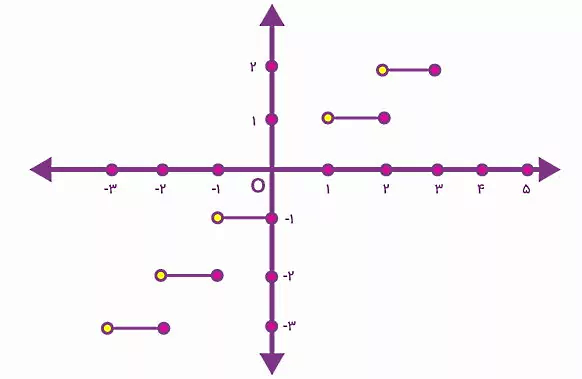
روش های تشخیص تابع در ریاضی
روشهای مختلفی برای تشخیص تابع بودن یک رابطه وجود دارد. در این بخش، به معرفی سه روش اصلی تشخیص تابع میپردازیم.
تشخیص تابع به روش حل Y
یکی از سادهترین روشهای تشخیص تابع بودن معادله، حل آن برای به دست آوردن خروجی y بر اساس ورودیهای مختلف x است. به عنوان مثال، معادلات زیر را در نظر بگیرد:
معادله ، یک تابع است؛ چراکه با قرار دادن هر ورودی دلخواه، مقدار y یک واحد بیشتر از x خواهد بود. معادله نیز به عنوان یک تابع در نظر گرفته میشود؛ زیرا با قرار دادن مقادیر ورودی دلخواه، yهای متفاوت به دست میآید. البته در و ، خروجی y برابر با ۰ میشود. با این وجود، هیچ کدام از این xها، خروجی دیگری را ایجاد نمیکنند.
از میان معادلات بالا، تنها را نمیتوان به عنوان یک تابع در نظر گرفت. برای اثبات این ادعا، یک ورودی دلخواه نظیر را درون معادله قرار میدهیم:
همانطور که مشاهده میکنید، برای یک مقدار دلخواه ورودی ()، دو جواب متفاوت ( و ) به دست آمد.
تشخیص تابع به روش آزمون خط عمودی
«آزمون خط عمودی» (Vertical Line Test)، روشی برای تشخیص تابع بودن یک رابطه از روی نمودار آن است. هیچ خط عمودی را نمیتوان یافت که نمودار یک تابع را در بیش از یک نقطه قطع کند.
در صورت برخورد خط عمودی به دو یا چند نقطه، نمودار رابطه، بیانگر یک تابع نیست. به عنوان مثال، دو نمودار زیر را در نظر بگیرد.
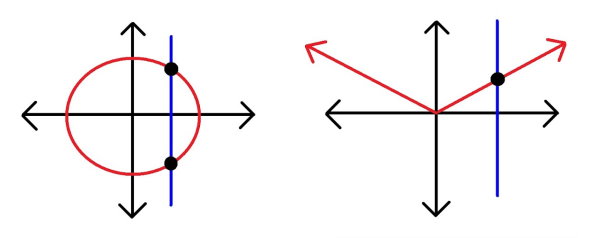
شکل سمت راست، نمودار یک تابع قدر مطلق را نمایش میدهد. شکل سمت چپ، نمودار حاصل از معادله دایره است. همانطور که مشاهده میکنید، خط عمودی، معادله دایره را در دو نقطه قطع میکند. بنابراین، معادله دایره، یک تابع نیست.
تشخیص تابع به روش جدولی
سومین روش برای تشخیص تابع بودن یک رابطه، استفاده از جدول حاوی ورودیها و خروجیهای آن رابطه است. در بخشهای قبلی دیدیم که امکان نمایش رابطه در قالب یک جدول وجود دارد. یکی از ستونها یا ردیفهای جدول، به پارامترهای دامنه و ستون یا ردیف دیگر، به پارامترهای برد اختصاص داده میشود. در صورت وجود ورودیهای تکراری، رابطه مورد بررسی، تابع نخواهد بود. به عنوان مثال، جدول زیر را در نظر بگیرید. این جدول، رابطه بین متغیر مستقل x و متغیر وابسته y را نمایش میدهد.
| متغیر مستقل x | متغیر وابسته y |
| ۲ | ۳ |
| ۴ | ۶ |
| ۸ | ۱۲ |
| ۱۶ | ۲۴ |
| ۳۲ | ۴۸ |
| ۶۴ | ۹۶ |
رابطه بین متغیر x و y در جدول بالا، معرف یک تابع است؛ چراکه هیچ یک از ورودیها در ستون مربوط به متغیر مستقل تکرار نمیشود. اکنون، جدول زیر را در نظر بگیرد.
| متغیر مستقل x | متغیر وابسته y |
| ۲ | ۳ |
| ۲ | ۳- |
| ۴ | ۶ |
| ۴ | ۶- |
| ۸ | ۱۶ |
| ۸ | ۱۶- |
رابطه بین متغیر x و y در جدول بالا، تابع نیست؛ زیرا ورودیهای رابطه در ستون مربوط به متغیر مستقل، تکرار میشوند. به عنوان مثال، عدد ۲، دو بار در ستون ورودیها ظاهر شده است. به عبارت دیگر، با قرار دادن عدد ۲ در این رابطه، به دو خروجی متفاوت میرسیم. این رفتار، با تعریف تابع تناقض دارد.
تفاوت دامنه، برد و هم دامنه در تابع
دامنه، برد و همدامنه از مهمترین مفاهیم مرتبط با مبحث تابع در ریاضی هستند. این مفاهیم، ارتباط بسیار نزدیکی به هم دارند. تصویر زیر، رابطه بین دو مجموعه را نمایش میدهد. مجموعه سمت چپ، اسم افراد و مجموعه سمت راست، سال تولد آنها است:
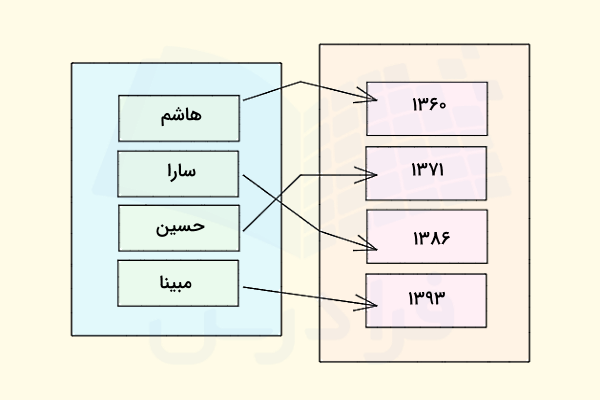
رابطه بالا، یک تابع است. مجموعه زوج مرتبهای این تابع به صورت زیر نوشته میشود:
{(۱۳۹۳ ,مبینا) ,(۱۳۷۱ ,حسین) ,(۱۳۸۶ ,سارا) ,(۱۳۶۰ ,هاشم)} = f
در ادامه، دامنه، برد و همدامنه را به کمک مثال بالا تعریف میکنیم.
دامنه تابع چیست؟
«دامنه» (Domain)، مجموعهای از تمامی مقادیر احتمالی و قابل قبول به عنوان ورودی یک تابع است. دامنه، به صورت مجموعه تمام مقادیر احتمالی برای متغیرهای مستقل نیز تعریف میشود. برای مثال ابتدای این بخش، مجموعه دامنه تابع، عبارت است از:
{(۱۳۹۳ ,مبینا) ,(۱۳۷۱ ,حسین) ,(۱۳۸۶ ,سارا) ,(۱۳۶۰ ,هاشم)} = f
{مبینا ,حسین ,سارا ,هاشم} = دامنه f
در واقع، تمام مولفههای اول تابع، در مجموعه دامنه قرار میگیرند. اگر مولفههای اول تابع مشخص نباشند، تعیین دامنه، با بررسی مقادیر مجاز برای قرار دادن در فرمول تابع صورت میگیرد. به عنوان مثال، تابع زیر را در نظر بگیرید:
ورودی تابع یا همان متغیر مستقل x، میتواند هر عدد حقیقی دلخواه باشد. بنابراین میگوییم دامنه تابع f(x)، مجموعه اعداد حقیقی (R) است. اکنون، یک تابع گویا، مانند تابع زیر را در نظر بگیرید:
میدانیم که مخرج هیچ کسری نمیتواند برابر با صفر باشد. بنابراین، مخرج کسر در تابع بالا (یعنی x) نمیتواند برابر با صفر باشد. به این ترتیب، میگوییم دامنه تابع f(x)، مجموعه اعداد حقیقی، به غیر از عدد ۰ است. تعیین دامنه تابع جذر نیز به همین صورت انجام میشود. عدد زیر رادیکال، نمیتواند یک عدد منفی باشد. از اینرو، همان تعیین دامنه توابع جذری، عبارت زیر رادیکال را بزرگتر یا مساوی صفر قرار میدهیم.
برد تابع چیست؟
«برد» (Range)، مجموعهای از تمام خروجیهای یک تابع است که بعد از جایگذاری ورودیها در آن تابع به دست میآید. برای مثال ابتدای این بخش، مجموعه برد تابع عبارت است از:
{(۱۳۹۳ ,مبینا) ,(۱۳۷۱ ,حسین) ,(۱۳۸۶ ,سارا) ,(۱۳۶۰ ,هاشم)} = f
{۱۳۹۳ , ۱۳۷۱ , ۱۳۸۶ ,۱۳۶۰} = برد f
به عبارت دیگر، تمام مولفههای دوم تابع به عنوان برد در نظر گرفته میشوند. در صورت داشتن فرمول تابع، مجموعه برد آن طی مراحل زیر به دست میآید:
- تغییر متغیر
- بازنویسی فرمول تابع برای محاسبه x
- تعیین دامنه تابع جدید (برد تابع قبلی)
به عنوان مثال، تابع زیر را در نظر بگیرید:
به منظور تعیین برد این تابع، ابتدا f(x) را برابر با y قرار میدهیم:
سپس، فرمول تابع را برای محاسبه x بازنویسی میکنیم:
میدانیم که عبارت زیر رادیکال نمیتواند منفی باشد. بنابراین:
در نتیجه، مقدار y یا همان خروجی تابع نمیتواند کوچکتر از ۱ باشد. به عبارت دیگر، برد تابع بالا برابر با ۱+ تا است.
هم دامنه تابع چیست؟
«همدامنه» (Codomain)، مجموعهای از تمام خروجیهای احتمالی به عنوان خروجی یک تابع است. در برخی از موارد، برد و همدامنه تابع، با یکدیگر برابر میشوند. به عنوان مثال، تابع زیر را در نظر بگیرید:
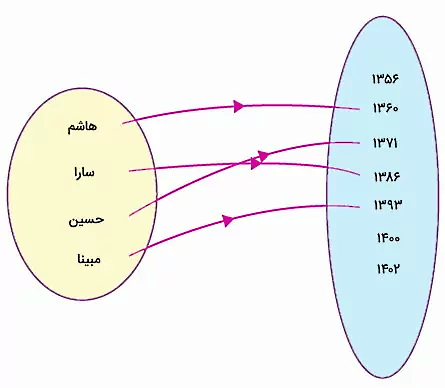
دامنه و برد تابع بالا عبارت هستند از:
{(۱۳۹۳ ,مبینا) ,(۱۳۷۱ ,حسین) ,(۱۳۸۶ ,سارا) ,(۱۳۶۰ ,هاشم)} = f
{مبینا ,حسین ,سارا ,هاشم} = دامنه f
{۱۳۹۳ , ۱۳۷۱ , ۱۳۸۶ ,۱۳۶۰} = برد f
همانطور که مشاهده میکنید، برد تابع، تمام اعضای مجموعه سمت راست (خروجیهای تابع) را شامل نمیشود. این مجموعه، همدامنه تابع است:
{۱۴۰۲ ,۱۴۰۰ ,۱۳۹۳ , ۱۳۷۱ , ۱۳۸۶ ,۱۳۶۰} = هم دامنه f
همدامنه، تمام خروجیهای احتمالی تابع را در برمیگیرد. مفهوم همدامنه، معمولا برای توابعی است که با عبارتهای شرطی نوشته میشوند. به عنوان مثال، تابع زیر را در نظر بگیرید:
دامنه و همدامنه تابع بالا را برابر با مجموعه اعداد صحیح در نظر بگیرید. به این ترتیب، داریم:
{ ... ,۳ ,۲ ,۱ ,۰ , ۱- ,۲- ,۳- , ...} =دامنه f(x)
{ ... ,۳ ,۲ ,۱ ,۰ , ۱- ,۲- ,۳- , ...} =همدامنه f(x)
با وجود اینکه مجموعه اعداد صحیح را به عنوان همدامنه در نظر گرفتیم، با قرار دادن اعضای دامنه در تابع، فقط به اعداد زوج میرسیم. به عبارت دیگر، برد تابع برابر است با:
{ ... ,۶ ,۴ ,۲ ,۰ , ۲- ,۴- ,۶- , ...} =برد f(x)
خروجی تابع چگونه به دست می آید؟
روشهای مختلفی برای به دست آوردن ورودی و خروجی انواع تابع در ریاضی وجود دارد. فرض کنید فرمول تابع و یکی از مقادیر ورودی آن را داریم. در این شرایط، با قرار دادن ورودی در فرمول تابع، خروجی آن به دست میآید. به عنوان مثال، تابع زیر را در نظر بگیرید:
این تابع، یک تابع چندجملهای درجه دو است (در بخش بعدی به معرفی این تابع و دیگر انواع تابع در ریاضی خواهیم پرداخت). اگر مقدار ورودی را برابر با ۳ قرار دهیم () و تابع را حل کنیم، خواهیم داشت:
بنابراین، خروجی تابع f(x) در برابر با ۲۲- است. به همین ترتیب، اگر خروجی تابع را داشتیم، میتوانستیم مقدار ورودی آن را به دست بیاوریم. به عنوان مثال، فرض کنید یکی از خروجیهای تابع f(x) برابر با ۷- باشد. در این حالت، مقدار ورودی (x) برابر خواهد بود با:
به عبارت دیگر:
مثال ۱
تابع f(x) عبارت است از:
خروجی تابع در مقادیر زیر را به دست بیاورید:
- ۲
- a
- a + h
در انتها، حاصل عبارت را تعیین کنید.
پاسخ
برای به دست آوردن خروجی تابع، هر یک از مقادیر بالا را به عنوان ورودی درون f(x) قرار میدهیم. برای ، داریم:
به منظور تعیین خروجی تابع در خواهیم داشت:
خروجی f(x) در نیز عبارت است با:
برای تعیین ، از خروجیهای به دست آمده از مراحل قبل استفاده میکنیم. بر اساس این خروجیها:
مثال ۲
رابطه را به صورت تابعی از n بنویسید.
پاسخ
برای نوشتن رابطه بالا به صورت تابعی از n، باید آن را بر حسب p بازنویسی کنیم. به این منظور، عبارت دارای p را در یک طرف رابطه نگه میداریم و باقی عبارتها را به طرف دیگر انتقال میدهیم:
در نتیجه:
مثال ۳
جدول زیر، مقادیر ورودی و خروجی تابع g(n) را نمایش میدهد.
| ورودی n | خروجی g(n) |
| ۱ | ۸ |
| ۲ | ۶ |
| ۳ | ۷ |
| ۴ | ۶ |
| ۵ | ۸ |
با توجه به جدول، مقدار پارامترهای زیر را به دست بیاورید:
- g(3)
- n در
پاسخ
منظور از g(3)، خروجی تابع g(n) در ورودی است. بر اساس مقادیر جدول، در ردیف ، مقدار خروجی g(n) برابر با ۷ میشود. بنابراین:
برای تعیین n در ، به ستون خروجی g(n) در جدول نگاه کرده و عدد ۶ را پیدا میکنیم. عدد ۶، در دو ردیف با و ظاهر میشود. در نتیجه:
ترکیب توابع چیست؟
«ترکیب توابع» (Composition of Functions)، فرآیند ادغام دو یا چند تابع در یک تابع منفرد است. به تابع حاصل از ترکیب توابع، «تابع مرکب» (Composite Function) میگویند. ترکیب دو تابع f(x) و g(x)، به صورت یا نوشته میشود. در اینجا، خروجی تابع g(x)، به عنوان ورودی در تابع f(x) قرار داده شده است:
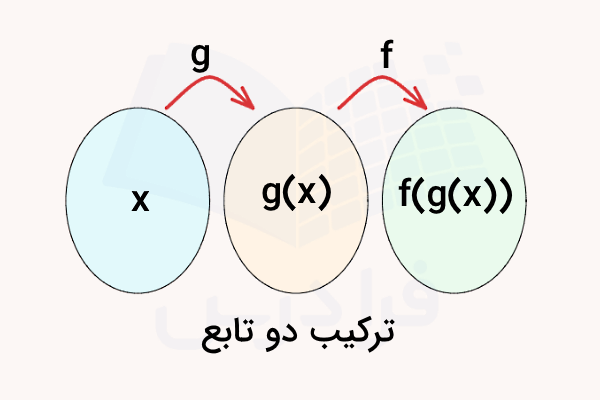
حاصل ترکیب توابع چگونه به دست می آید؟
برای به دست آوردن حاصل ترکیب دو تابع، ابتدا باید مقدار تابع درونی را محاسبه کنیم. سپس، خروجی تابع درونی را به عنوان ورودی در تابع بیرونی قرار دهیم. به عنوان مثال، دو تابع زیر را در نظر بگیرد:
به منظور تعیین ، ابتدا را به عنوان ورودی در قرار میدهیم:
خروجی برابر با 6- شد. این خروجی را به عنوان ورودی، به جای x در جایگزین میکنیم:
انواع تابع در ریاضی
توابع مختلفی در دنیای ریاضی وجود دارند که از مهمترین آنها میتوان به توابع خطی، چندجملهای، توانی، مثلثاتی، وارون و لگاریتمی اشاره کرد. معیارهای مختلفی برای تقسیمبندی انواع تابع در ریاضی وجود دارند. بر اساس این معیارها، توابع مختلف به چهار گروه اصلی تقسیم میشوند:
- انواع تابع بر اساس رابطه بین دامنه و برد: تابع یک به یک، تابع چند به یک، تابع پوشا، تابع یک به یک و پوشا، تابع غیرپوشا و تابع ثابت
- انواع تابع بر اساس فرم معادله: تابع همانی، تابع خطی، تابع درجه دو یا مربعی، تابع درجه سه یا مکعبی و تابع چندجملهای
- انواع تابع بر اساس برد: تابع قدر مطلق، تابع گویا، تابع علامت، تابع فرد، تابع زوج، تابع متناوب یا دورهای، تابع جز صحیح، تابع وارون و تابع مرکب
- انواع تابع بر اساس دامنه: تابع جبری، تابع مثلثاتی و تابع لگاریتمی
در این بخش، به معرفی این توابع و دیگر انواع تابع در ریاضی خواهیم پرداخت.
تابع چند جمله ای
«تابع چند جملهای» (Polynomials Functions)، یکی از طبقهبندیهای گسترده و کلی در مبحث تابع در ریاضی است. بسیاری از توابع ریاضی در گروه چندجملهایها قرار میگیرند. توابع چندجملهای، مطابق با فرم زیر نوشته میشوند:
n، درجه چندجملهای و ، ضریب پیشرو است. شروط زیر در فرم کلی تابع چندجملهای صدق میکنند:
- و عضوی از مجموعه اعداد صحیح است.
- ، ضرایب ثابت هستند.
البته، استثناهایی برای شروط بالا وجود دارند. به عنوان مثال، اگر باشد، الزام شرط سوم () از بین میرود. در صورت ۰ بودن ، تابع f(x) نیز برابر با صفر خواهد بود:
در این حالت، به f(x)، «تابع صفر» (Zero Function) میگویند. توابع چندجملهای با درجه متفاوت، عناوین مخصوص به خود را دارند. تا به اینجا دیدیم که به تابع چندجملهای با درجه ۰، تابع صفر میگویند. اگر درجه تابع چندجملهای برابر با ۱ باشد، به آن تابع خطی میگویند. یکی از فرمهای تابع خطی را در نظر بگیرید:
همانطور که مشاهده میکنید، توابع خطی، یکی از انواع توابع چندجملهای هستند. البته، باید دو شرط زیر در معادله تابع خطی برقرار باشد تا بتوان آن را به عنوان تابع چندجملهای در نظر گرفت:
- تابع خطی، یک تابع چندجملهای با درجه ۱ است؛ اگر باشد.
- تابع خطی، یک تابع چندجملهای با درجه ۰ است؛ اگر باشد.
تابع چندجملهای درجه دو، یک تابع مهم در ریاضی است که احتمالا با آن زیاد سر و کار خواهید داشت. این تابع با عنوان «تابع مربعی» (Quadratic Function) نیز شناخته میشود. فرم کلی معادله تابع درجه دو به صورت زیر است:
در معادله درجه دو، a نمیتواند برابر با ۰ باشد. آخرین تابع چندجملهای که در اینجا معرفی میکنیم، تابع درجه ۳ است. این تابع با عنوان «تابع مکعبی» (Cubic Function) نیز شناخته میشود. فرم استاندارد این تابع به صورت زیر نوشته میشود:
تابع جبری
جمع، تفریق، ضرب، تقسیم، توان و جذر ، علائمی هستند که در بسیاری از معادلات و فرمولهای ریاضی مورد استفاده قرار میگیرند. به توابعی که رابطه آنها به کمک این علائم جبری نمایش داده شود، «تابع جبری» (Algebraic Function) میگویند. توابع زیر، نمونههایی از انواع تابع جبری هستند:
بسیاری از انواع تابع در ریاضی، زیرمجموعهای از توابع جبری هستند. البته، توابع قدر مطلق، نمایی، لگاریتمی و مثلثاتی را نمیتوان به عنوان توابع جبری در نظر گرفت.
تابع جبری گویا چیست؟
«تابع گویا» (Rational Function)، یکی از انواع توابع جبری است که اعداد گویا، به صورت کسری نمایش داده میشوند. فرم کلی معادله یک تابع گویا عبارت است از:
صورت و مخرج توابع گویا (p(x) و q(x) در معادله بالا)، توابع چندجملهای هستند. به عنوان مثال، دو تابع زیر را در نظر بگیرید:
f(x) و g(x)، دو تابع جبری گویا به شمار میروند. اگر صورت و مخرج تابع گویا، یک چندجملهای درجه یک باشد، به آن «تابع هموگرافیک» (Homographic Function) میگویند.
تابع جذر چیست؟
تابع جذر» (Root Function)، یکی دیگر از انواع توابع جبری است که مطابق با فرم زیر نوشته میشود:
فرم کلی تابع جذر به صورت زیر است:
b ،h ،a و k، ثابتهای عددی هستند. r، ریشه رادیکال را نمایش میدهد. به صورت پیشفرص، ریشه رادیکال برابر با ۲ در نظر گرفته میشود؛ مگر اینکه به مقدار آن اشاره شده باشد.
تابع توانی
«تابع توانی» (Power Function)، تابعی با یکجملهای با توان غیرصفر است. رابطه زیر، فرم استاندارد تابع توانی را نمایش میدهد:
بر اساس تعریف، p و k، دو ثابت عددی غیرصفر هستند. اگر p، زوج باشد، به تابع ، یک «تابع زوج» (Even Function) میگوییم. مقدار x در نمودار توابع زوج، همواره مثبت است؛ چراکه در این تابع، داریم:
در صورت فرد بودن p، تابع ، با عنوان «تابع فرد» (Odd Function) شناخته میشود. مقدار x در نمودار توابع فرد، میتواند مثبت یا منفی باشد؛ زیرا در این تابع، داریم:
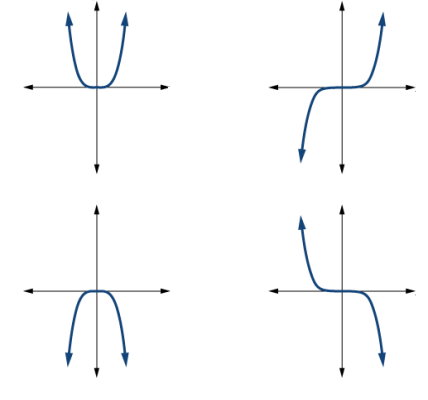
تصویر زیر، شکل کلی انواع توابع توانی را بر حسب زوج یا فرد بودن توان و منفی یا مثبت بودن ضریب k نشان میدهد.
تابع مثلثاتی
به توابعی که رابطه بین زوایا و ضلعهای مثلث قائمالزاویه را مشخص میکنند، «توابع مثلثاتی» (Trigonometric Functions) میگویند. توابع مثلثاتی، اهمیت بسیار زیادی در ریاضیات و کاربرد آن در حوزههای مختلف دارند. این توابع، تقریبا در تمام علوم مهندسی و حتی علوم پایه نیز مورد استفاده قرار میگیرند.
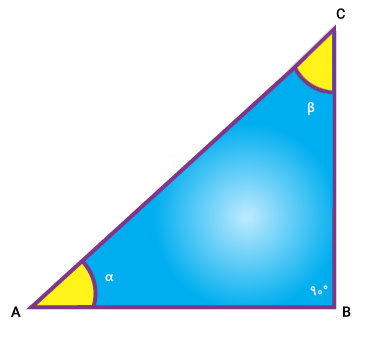
در یک مثلث قائمالزاویه نظیر مثلث ABC در تصویر بالا، نسبتهای مثلثاتی به صورت زیر نوشته میشوند:
عبارتهای مورد استفاده در روابط بالا عبارت هستند از:
- A: زاویه راس A (یکی از زاویههای حاده مثلث قائمالزاویه)
- : سینوس زاویه راس A
- : کسینوس زاویه راس A
- : تانژانت زاویه راس A
- : کتانژانت زاویه راس A
- : سکانت زاویه راس A
- : کسکانت زاویه راس A
- BC: ضلع مقابل به زاویه راس A
- AB: ضلع مجاور به زاویه راس A
- AC: وتر مثلث قائمالزاویه
فرم جبری توابع بالا، مشابه با دیگر انواع تابع در ریاضی نوشته میشود. به عنوان مثال، فرمول جبری معرف تابع سینوس عبارت است از:
ورودی x، به صورت زاویه با یکای درجه یا رادیان در تابع مثلثاتی سینوس قرار میگیرد. خروجی این تابع، عددی بین ۱- تا ۱ است. برای آشنایی بیشتر با توابع مثلثاتی، مطالعه مطالب زیر را به شما پیشنهاد میٰکنیم:
- قوانین مثلثات به زبان ساده + مثال و تمرین
- نسبتهای مثلثاتی به زبان ساده + مثال و تمرین
- اثبات روابط مثلثاتی – به زبان ساده
- اتحادهای مثلثاتی + اثبات اتحادها و نمونه سوال با جواب
- روابط مثلثاتی و فرمولهای مثلثاتی مهم + دانلود PDF خلاصه رایگان
- مشتق توابع مثلثاتی | به زبان ساده
- انتگرال مثلثاتی – به زبان ساده + مثال و تمرین
- نمونه سوال مثلثات — همراه با جواب (+ دانلود فیلم آموزش رایگان)
- تقلب نامه (Cheat Sheet) مقادیر و فرمول های مثلثاتی
- تابع معکوس مثلثاتی — به زبان ساده
- مشتق توابع معکوس مثلثاتی — به زبان ساده
- معادلات مثلثاتی — به زبان ساده
- آموزش مثلثات — مجموعه مقالات جامع وبلاگ فرادرس
- رسم نمودار سینوس و کسینوس – به زبان ساده با مثال و تمرین
- نمودار تانژانت و کتانژانت – به زبان ساده با مثال و تمرین
تابع نمایی
اگر متغیر ورودی x به صورت توان در فرمول تابع ظاهر شود، «تابع نمایی» (Exponential Function) به وجود میآید.
فرم کلی تابع نمایی به صورت زیر نوشته میشود:
b ،a و c، ثابتهای عددی هستند. البته مقدار عددی b نمیتواند ۰ یا ۱ باشد. به عبارت دیگر، در یک تابع نمایی، داریم:
و
در صورت ۰ یا ۱ بودن b در تابع بالا، خروجی f(x) برابر با یک مقدار ثابت میشود. اگر b برابر با عدد اویلر () باشد، به f(x)، تابع نمایی طبیعی میگویند. فرم کلی تابع نمایی طبیعی عبارت است از:
تابع لگاریتمی
«تابع لگاریتمی» (Logarithmic Function)، یکی دیگر از توابع معروف در ریاضی است که وارون تابع نمایی را نمایش میدهد. فرم استاندارد این تابع به صورت زیر است:
a، با عنوان «مبنای لگاریتم» شناخته میشود. در صورت مشخص نبودن a، مقدار پیشفرض آن را برابر با ۱۰ در نظر میگیریم. اگر مبنای لگاریتم برابر با عدد اویلر () باشد، فرم تابع لگاریتمی به شکل زیر درمیآید:
به ، تابع لگاریتم طبیعی میگویند.
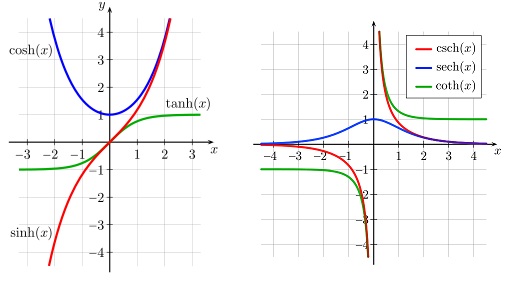
تابع هیپربولیک
توابع هذلولی یا «توابع هیپربولیک» (Hyperbolic Functions)، توابعی مشابه توابع مثلثاتی هستند که بر اساس معادلات هذلولی و تابع نمایش نوشته میشوند.
به عنوان مثال، معادله سینوس هیپربولیک عبارت است از:
تصویر زیر، نمودار انواع توابع هیپربولیک را نمایش میدهد.
تابع وارون
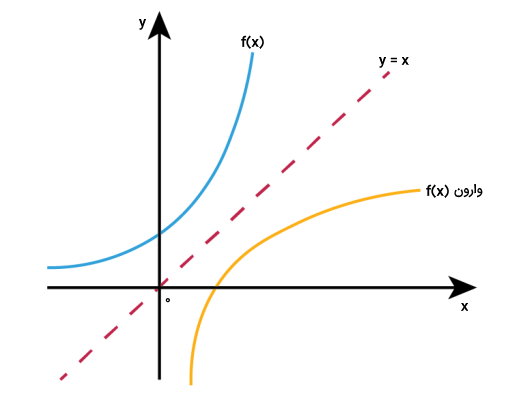
«تابع وارون» (Inverse Function)، تابعی است که عملکرد معکوس یک تابع دیگر را نمایش میدهد. به عنوان مثال، فرض کنید ، تابع وارون است. به این ترتیب:
- خروجی با ورودی برابر میشود.
- ورودی با خروجی برابر میشود.
نمودار وارون یک تابع، دارای تقارن محوری با نمودار اصلی آن تابع است.
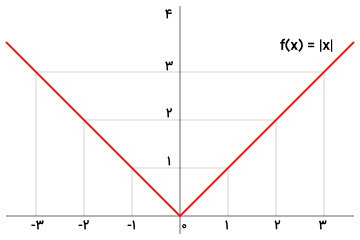
تابع قدر مطلق
«تابع قدر مطلق» (Modulus Function یا Absolute Value Function)، تابع با خروجی غیرمنفی است. به عبارت دیگر، صرفنظر مثبت یا منفی بودن علامت ورودی، خروجی این تابع برابر با یک مقدار غیرمنفی (۰ یا مثبت) میشود. سادهترین فرم تابع قدر مطلق عبارت است از:
تابع جز صحیح یا تابع پله ای
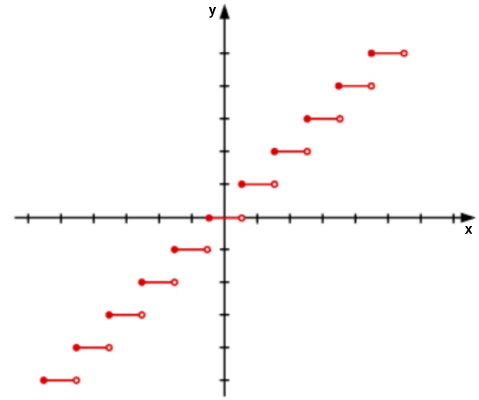
«تابع پلهای» (Step Function)، «تابع بزرگترین جز صحیح» (Greatest Integer Function) یا تابع جز صحیح، تابعی با خروجیهای صحیح است. این تابع، ورودی دلخواه (حقیقی) را به کوچکترین عدد صحیح مجاور تبدیل میکند. سادهترین فرم تابع جز صحیح به صورت زیر نوشته میشود:
به عنوان مثال، خروجی این تابع در برابر با ۱ (کوچکترین عدد صحیح مجاور) است. تصویر زیر، نمودار تابع جز صحیح را نمایش میدهد.
تابع علامت
«تابع علامت» (Signum Function)، تابعی با خروجی ۱+، ۰ یا ۱- است. این تابع، به منظور تعیین علامت توابع دیگر مورد استفاده قرار میگیرد.
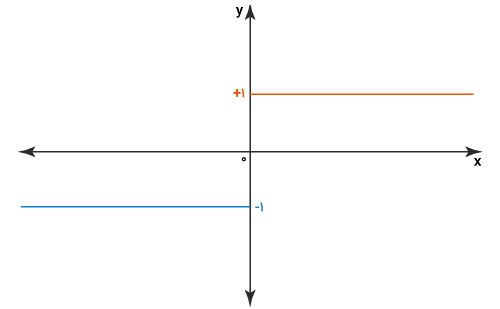
تابع علامت به صورت زیر نمایش داده میشود:
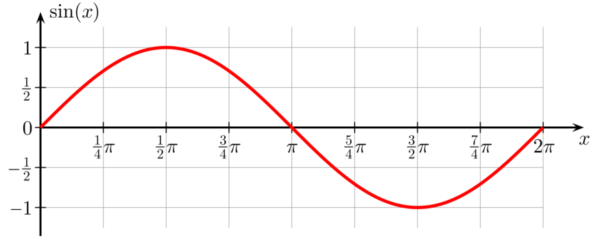
تابع متناوب
به تابعی که خروجی آن در بازههای منظم تکرار شود، «تابع متناوب» (Periodic Function) میگویند. توابع مثلثاتی، شناخته شدهترین انواع تابع متناوب هستند. فرم توابع متناوب به صورت زیر نوشته میشود.
P، دوره تناوب (بازه تکرار رفتار تابع) را نمایش میدهد. به عنوان مثال، در یک تابع سینوسی، پس از هر ۳۶۰ درجه، رفتار تابع تکرار میشود.
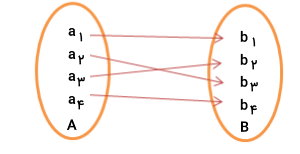
تابع یک به یک
«تابع یک به یک» (One-to-One Function یا Injective Function)، تابعی است که هر یک از خروجیهای آن، فقط به یکی از ورودیها وصل میشود. به عبارت دیگر، تابع یک به یک، خروجی تکراری ندارد.
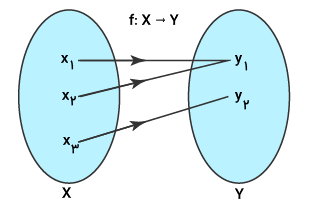
تابع چند به یک
«تابع چند به یک» (Many-to-One Function)، تابعی است که در آن، حداقل یک خروجی به دو یا چند ورودی وصل میشود. به عبارت دیگر، تابع چند به یک، خروجیهای تکراری دارد.
تابع پوشا
به تابعی که تمام خروجیهای آن با حداقل یک ورودی در ارتباط باشد، «تابع پوشا» (Onto Function یا Surjective Function) میگویند. در تابع پوشا، برد و همدامنه برابر هستند.
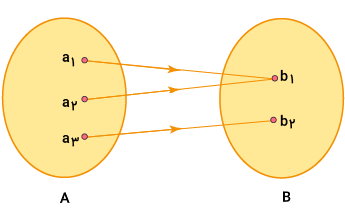
تابع یک به یک و پوشا چیست ؟
«تابع یک به یک و پوشا» (Onto and One-to-One Function) یا «تابع دوسویی» (Bijective Function)، تابعی است که از ویژگیهای تابع یک به یک و تابع پوشا بهره میبرد. در این تابع، هر خروجی، تنها به یک ورودی وصل میشود. به علاوه، تمام مولفههای خروجی و ورودی با یکدیگر در ارتباط هستند.

تابع غیر پوشا
«تابع غیرپوشا» (Into Function)، تابعی است که حداقل یکی از اعضای برد آن، با هیچ یک از اعضای دامنه ارتباط ندارد. به عبارت دیگر، برد و همدامنه تابع غیرپوشا با یکدیگر برابر نیستند.
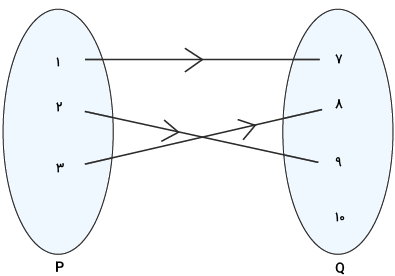
تابع ثابت
«تابع ثابت» (Constant Function)، تابعی با خروجی ثابت است. به عبارت دیگر، با قرار دادن هر مقدار ورودی در این تابع، همواره یک خروجی ثابت به دست میآید. فرم استاندارد تابع ثابت به صورت زیر نوشته میشود:
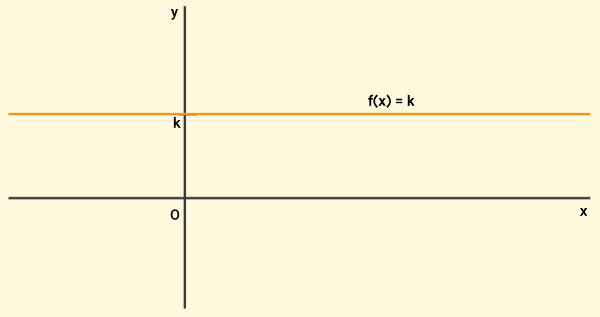
تابع صعودی و تابع نزولی چیست؟
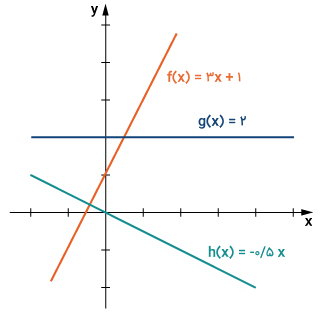
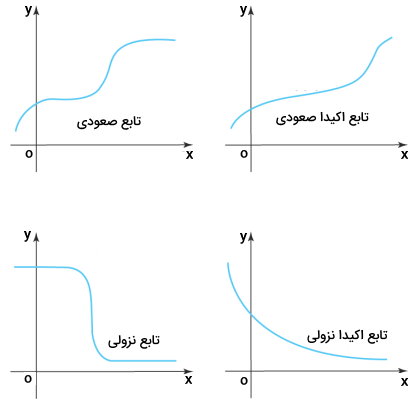
اگر با افزایش مقدار ورودی، مقدار خروجی تابع افزایش یابد، به آن تابع، «تابع صعودی» (Increasing Function) میگویند. در صورت کاهش مقدار خروجی تابع با افزایش مقدار ورودی آن، تابع با عنوان «تابع نزولی» (Decreasing Function) شناخته میشود. تصویر زیر، شکل کلی نمودارهای توابع صعودی و نزولی را نمایش میدهد.
تابع همانی
«تابع همانی» (Identity Function)، تابعی است که در آن، خروجی تابع با ورودی برابر میشود. به عبارت دیگر:
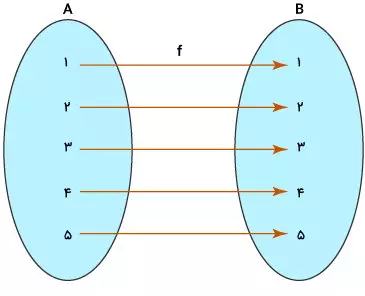
کاربرد تابع در علوم کامپیوتر
توابع ریاضی، در علوم کامپیوتر و بسیاری از حوزههای درگیر با محاسبات ریاضی کاربرد دارند. زبانهای برنامهنویسی، از مفهوم تابع برای تعریف عملکردهای مختلف یک برنامه استفاده میکنند. فرم توابع زبانهای برنامهنویسی با کتابهای ریاضی شباهتها و تفاوتهایی دارد. به عنوان مثال، عبارتهای زیر، چند نمونه از توابع مهم در زبان برنامهنوسی پایتون هستند:
همانطور که مشاهده میکنید، برخلاف توابع ریاضی، عنوان توابع پایتون، یک عبارت چندحرفی است. البته مشابه با توابع ریاضی، ورودی توابع پایتون میتواند درون پرانتز قرار گیرد. در صورت تمایل به آشنایی بیشتر و بهتر با مفهوم توابع زبانهای مختلف برنامهنویسی، مطالعه مطلب «تابع در برنامه نویسی چیست؟ — به زبان ساده» را به شما پیشنهاد میکنیم.
تابع در اکسل
مفهوم تابع در علوم کامپیوتر، به حوزه برنامهنویسی محدود نمیشود. بسیاری از نرمافزاهای کامپیوتری، مخصوصا نرمافزارهای مرتبط با محاسبات ریاضی، از توابع این مفهوم پرکاربرد بهره میبرند. از پرکاربردترین نرمافزارهای کامپیوتری دارای قابلیت فرمولنویسی و تعریف تابع، میتوان به اکسل اشاره کرد. اکسل، معروفترین و محبوبترین نرمافزار صفحه گسترده است که به منظور ساخت دادههای جدولی و تحلیل آنها مورد استفاده قرار میگیرد. از قابلیتهای کاربردی این نرمافزار میتوان به فرمولنویسی و ساخت توابع اشاره کرد. فرم وارد کردن و استفاده از توابع اکسل، به زبانهای برنامهنویسی شباهت دارد.

سوالات متداول در مورد تابع در ریاضی
در انتهای این مطلب از مجله فرادرس و پس از اینکه کاملا متوجه شدید تابع چیست، در این بخش، به برخی از پرتکرارترین سوالات مرتبط با محبث تابع در ریاضی به طور خلاصه پاسخ میدهیم.
تعریف تابع چیست؟
تابع، رابطهای است که مجموعهای از ورودیها (دامنه) را به مجموعهای از خروجیها (برد یا همدامنه) متصل میکند؛ به طوری که تمام خروجیها، فقط به یکی از ورودیها وصل شده باشند.
تابع در ریاضی با چه علامتی نمایش داده می شود؟
تابع در ریاضی با حروفی مانند g ،f و h نمایش داده میشود.
فرمول تابع چیست؟
فرمول کلی رابطه تابع، معمولا به فرم y=f(x) است. x، به عنوان متغیر ورودی و y، به عنوان متغیر خروجی در نظر گرفته میشود.
انواع تابع در ریاضی چه هستند؟
از مهمترین انواع تابع در ریاضی میتوان به توابع جبری، چندجملهای (خطی، مربعی، مکعبی)، مثلثاتی، لگاریتمی، نمایی، یک به یک، وارون و قدر مطلق اشاره کرد.
تعریف دامنه تابع چیست؟
دامنه، مجموعه مقادیر مجاز ورودی تابع برای به دست آوردن مقادیر خروجی مجاز است.
تعریف برد تابع چیست؟
برد، مجموعه خروجیهای حاصل از قرارگیری مقادیر دامنه در تابع است.
تعریف هم دامنه تابع چیست؟
همدامنه یا پاددامنه، مجموعهای از تمام خروجیهای احتمالی تابع است که مقادیر برد تابع باید در آن قرار داشته باشند.
آیا برد و هم دامنه تابع برابر هستند؟
برد و همدامنه تابع از نظر تعریف با یکدیگر تفاوت دارند. به طور کلی، همدامنه، مجموعهای بزرگتر یا مساوی برد است که تمام مولفههای برد را دربرمیگیرد.
تابع چند جمله ای چیست؟
تابعی که از جمع یا تفریق چند عبارت با توان غیرمنفی و غیرکسری تشکیل شده باشد، تابع چندجملهای میگویند.
آزمون تابع
۱. ویژگی یکتایی خروجی برای هر ورودی در تابع به چه معناست؟
ورودیها و خروجیها الزاما باید عدد باشند.
برای هر ورودی میتواند چند خروجی وجود داشته باشد.
برای هر ورودی فقط یک خروجی مشخص وجود دارد.
هر خروجی میتواند به چند ورودی مربوط باشد.
مفهوم یکتایی خروجی یعنی اگر یک مقدار مشخص را به تابع بدهیم، فقط یک خروجی معین به دست میآوریم و هر ورودی نمیتواند چند خروجی مختلف داشته باشد. عبارت «برای هر ورودی فقط یک خروجی مشخص وجود دارد» این ویژگی را نشان میدهد. option «برای هر ورودی میتواند چند خروجی وجود داشته باشد» خلاف تعریف تابع است. عبارت «هر خروجی میتواند به چند ورودی مربوط باشد» بیانگر برعکس یا انواع دیگر روابط است اما درباره ویژگی یادشده نیست. جمله «ورودیها و خروجیها الزاما باید عدد باشند» نادرست است چون تابع میتواند ورودی یا خروجی غیر عددی هم داشته باشد.
۲. در ریاضیات، دامنه و برد یک تابع به چه صورت تعریف میشوند؟
دامنه همه ورودیهای مجاز تابع است و برد همه خروجیهای واقعی تابع میباشد.
دامنه و برد هر دو مجموعهای از جوابهای دلخواه تابع هستند.
دامنه همه عددهای مثبت است و برد همه خروجیهای ممکن تابع است.
دامنه همه پاسخهای تابع است و برد همه ورودیها میباشد.
تعریف صحیح آن است که «دامنه» مجموعه ورودیهای مجاز یک تابع را شامل میشود و «برد» مجموعهای است متشکل از همه خروجیهایی که واقعا با قرار دادن عناصر دامنه در تابع به دست میآید.
۳. کدام ویژگی مهم باعث میشود یک رابطه در ریاضی تابع تلقی نشود؟
هر ورودی بیش از یک خروجی داشته باشد.
هر خروجی فقط یک ورودی داشته باشد.
ورودیها از یک مجموعه ثابت انتخاب شوند.
خروجیها از مقادیر عددی باشند.
ویژگی «هر ورودی بیش از یک خروجی داشته باشد» باعث میشود رابطه تابع نباشد، زیرا برای تابع بودن باید هر ورودی فقط یک خروجی مشخص داشته باشد. در حالتی که «هر خروجی فقط یک ورودی داشته باشد»، یا ورودیها و خروجیها فقط از مجموعه خاصی انتخاب شوند، شرط تابع بودن نقض نمیشود. رابطهای که خروجیهای عددی دارد نیز همچنان میتواند تابع باشد؛ اما داشتن چند خروجی برای یک ورودی با تعریف تابع سازگار نیست.
۴. از نظر ساختاری، چه تفاوتی میان «رابطه» و «تابع» در ریاضیات وجود دارد؟
تابع همیشه به صورت فرمول جبری نمایش داده میشود اما رابطه شکل نموداری ندارد.
همه توابع لزوما برد و دامنه برابر دارند ولی رابطه این ویژگی را ندارد.
در رابطه هر ورودی میتواند چندین خروجی داشته باشد اما در تابع هر ورودی فقط یک خروجی دارد.
در تابع همه ورودیها باید عدد صحیح باشند ولی در رابطه این شرطی وجود ندارد.
وجه اصلی تفاوت میان رابطه و تابع این است که در «تابع» هر ورودی فقط به یک خروجی منحصر به فرد متصل میشود، اما در «رابطه» احتمال اینکه یک ورودی چند خروجی به همراه داشته باشد وجود دارد. این ویژگی یکتایی خروجی در تابع موجب تمایز آن از سایر روابط است و باعث میشود هر تابع یک نوع خاص از رابطه محسوب شود. عبارتهایی مانند شرط عدد صحیح بودن ورودیها یا لزوم نمایش جبری برای تابع صحیح نیستند و درباره تمام توابع و روابط صدق نمیکنند. همچنین تساوی دامنه و برد در تابع اجباری نیست و صرفا ویژگی برخی انواع خاص است، نه تعریف تابع یا رابطه.
۵. چگونه جدول مقادیر میتواند در تشخیص تابع بودن یک رابطه نقش داشته باشد؟
با بررسی نمودار نقاط جدول بر روی محور مختصات.
با استفاده از نامگذاری تابعی مانند f(x).
با مقایسه دامنه اعداد جدول با فرمول تابع.
با مشاهده اینکه هر ورودی فقط یک خروجی دارد.
اگر در جدول مقادیر مشاهده شود که هر ورودی فقط یک خروجی خاص دارد، میتوان نتیجه گرفت که این رابطه یک تابع است. حضور مقدارهای تکراری برای ورودیها که خروجیهای متفاوتی ایجاد کنند، نشان میدهد که آن رابطه تابع نیست. روشهای دیگر مانند صرفا نامگذاری تابعی یا نمایش نمودار بدون دقت به تکرار ورودیها، تضمینی برای تشخیص تابع بودن ایجاد نمیکنند. همچنین مقایسه دامنه با فرمول به تنهایی بیانگر یکتایی خروجی برای هر ورودی نیست.
۶. در نمایش تابع، تفاوت روش جبری با روش گرافیکی چیست؟
روش جبری تابع را با جدول مقدارها معرفی میکند، روش گرافیکی فقط شکل تابع را میکشد.
در روش جبری تابع با فرمول ریاضی نوشته میشود، اما در روش گرافیکی تابع با نمودار نمایش داده میشود.
روش جبری فقط برای اعداد صحیح مناسب است، ولی روش گرافیکی برای همه مقادیر استفاده میشود.
در روش جبری خروجیها مشخص نیستند، اما روش گرافیکی همیشه مقدار خروجی را نشان میدهد.
در روش جبری تابع را بهوسیله یک فرمول مانند f(x) نمایش میدهیم، اما در روش گرافیکی تابع را به صورت نمودار روی دستگاه مختصات ترسیم میکنیم. طبق توضیحات ارائهشده، تفاوت اصلی در نحوه نمایش و تجسم تابع است؛ بیان ریاضی در مقابل نمایش تصویری. عباراتی مانند «روش جبری فقط برای اعداد صحیح مناسب است» یا «خروجیها در روش جبری مشخص نیستند» نادرستاند، زیرا هر دو روش میتوانند ورودی و خروجیهای مختلف را پوشش دهند. همچنین در روش جبری اغلب جدول هم استفاده میشود ولی اصل آن فرمول است و نمایش تصویری به عهده روش گرافیکی است.
۷. در زندگی روزمره، چرا مفهوم تابع اهمیت زیادی دارد؟
چون تابع ارتباط یکتای ورودی و خروجی را تعریف میکند.
چون تابع فقط در حل معادلات ریاضی به کار میرود.
زیرا تابع فقط ساختار نمودارهای ریاضی را مشخص میسازد.
چون تابع فقط در علم فیزیک کاربرد دارد.
اهمیت تابع در زندگی روزمره به دلیل ارتباط یکتای بین ورودی و خروجی است؛ هر ورودی فقط یک خروجی میدهد. این ویژگی باعث میشود مفاهیمی مانند محاسبه دستمزد، رابطه ساعت کاری با حقوق یا قانون عرضه و تقاضا قابل پیشبینی و عملی شوند. بیان اینکه تابع فقط در حل معادلات یا فقط در فیزیک استفاده میشود، نادرست است و نیز تابع صرفا به ساختار نمودار محدود نمیشود. هم در ریاضیات و هم در کاربردهای واقعی، اصل تفاوت تابع همان تضمین یکتایی خروجی برای هر ورودی معتبر است.
۸. کدام عبارت به درستی تفاوت میان برد و همدامنه را در توابع بیان میکند؟
برد و همدامنه همیشه دقیقا برابرند و تفاوتی ندارند.
برد ورودیهای تابع و همدامنه خروجیهای وابسته به ورودی هستند.
برد مجموعه خروجیهایی است که واقعا حاصل میشود، اما همدامنه همه خروجیهای ممکن تعریف شده است.
برد تمام ورودیهای مجاز تابع است و همدامنه تنها خروجیهای خاص را نشان میدهد.
در مفهوم تابع، «برد» مجموعهای از خروجیهایی است که با قرار دادن عناصر دامنه در تابع به دست میآید و لزوما شامل تمام مقادیر ممکن تعریف شده نیست. در مقابل، «همدامنه» مجموعهای از تمام خروجیهایی است که تابع میتواند طبق تعریف داشته باشد (حتی اگر همه آنها در عمل تولید نشود). بنابراین «برد مجموعه واقعا تولیدشده» است و «همدامنه ممکنها» را شامل میشود. سایر عبارات اشتباهاند، چون برد و همدامنه همواره برابر نیستند و تعریف دامنه، برد و همدامنه بهصورت ورودی و خروجی متفاوت است.
۹. برای تشخیص تابع بودن یک نمودار، آزمون خط عمودی چگونه عمل میکند؟
اگر خط عمودی نمودار را فقط در یک نقطه قطع کند، آن نمودار یک تابع است.
اگر خط عمودی در دو نقطه یا بیشتر نمودار را قطع کند، حتما تابع است.
اگر نمودار با هیچ خط عمودی تلاقی نکند، آن رابطه تابع خواهد بود.
هر خط افقی روی نمودار فقط یک نقطه را قطع کند، آن نمودار تابع است.
بر اساس آزمون خط عمودی، اگر هر خط عمودی نمودار را فقط و فقط در یک نقطه قطع کند، نشان میدهد که برای هر ورودی فقط یک خروجی وجود دارد و رابطه تابع محسوب میشود. وجود بیش از یک نقطه تقاطع خط عمودی با نمودار یا نبودن تقاطع میان نمودار و خط عمودی، نشانه تابع نبودن یا تعریف نشدن تابع روی آن دامنه است. شرط قطع شدن در یک نقطه، به طور مستقیم شرط تابع بودن است.
۱۰. اگر در یک جدول مقادیر، دو مقدار متفاوت خروجی برای یک مقدار ورودی وجود داشته باشد، کدام نتیجه درست است؟
تابع بهدرستی تعریفشده و خروجی یکتا دارد.
برای هر ورودی، هر تعداد خروجی مجاز است.
جدول فقط به ورودیهای عددی نیاز دارد.
رابطه نشان دادهشده یک تابع نیست.
اگر برای یک مقدار ورودی، بیش از یک مقدار خروجی ظاهر شود، ویژگی یکتایی در تابع برقرار نیست. بنابراین، وجود دو مقدار خروجی برای یک ورودی یعنی ارتباط دادهشده تابع نیست و برخلاف تعریف تابع عمل شده است.
۱۱. در ترکیب توابع، اگر ابتدا خروجی تابع g وارد تابع f شود، ترتیب قرار دادن این توابع نسبت به زمانی که f و g را جابهجا کنیم چه تاثیری بر خروجی خواهد گذاشت؟
جابهجایی توابع f و g هیچ تاثیری بر خروجی ندارد.
همیشه خروجیها در هر دو حالت برابر هستند.
ترتیب قرارگیری توابع معمولا باعث تغییر خروجی نهایی ترکیب میشود.
فقط اگر هر دو تابع خطی باشند، ترتیب آنها مهم نیست.
در ترکیب توابع، ترتیب قرار دادن تابع g و سپس f اهمیت زیادی دارد، زیرا خروجی تابع g ابتدا محاسبه شده و سپس وارد تابع f میشود. اگر جای این دو تابع عوض شود، معمولا خروجی متفاوتی به دست میآید؛ زیرا ورودی و خروجیها جابهجا خواهند شد.
۱۲. برای به دست آوردن خروجی یک تابع از روی فرمول جبری آن، کدام فرایند باید انجام شود؟
تمام خروجیهای ممکن تابع را فهرست میکنیم و مقایسه مینماییم.
فرمول تابع را بر اساس خروجی بازنویسی میکنیم و مقدار اولیه را مییابیم.
فقط متغیرها و پارامترهای فرمول را بررسی و علامتگذاری میکنیم.
مقدار ورودی را در فرمول تابع جایگذاری میکنیم و محاسبه را انجام میدهیم.
در فرایند محاسبه خروجی تابع با داشتن فرمول جبری، باید مقدار ورودی دلخواه را در فرمول جایگذاری کرده و سپس عملیات ریاضی مربوط را انجام دهیم تا جواب نهایی به عنوان خروجی به دست آید.
۱۳. کدام عبارت نحوه تشخیص تابع چندجملهای را به درستی بیان میکند؟
فرمولی که همواره توابع مثلثاتی مثل سینوس در آن وجود دارد.
فرمولی که حتما یک جزء به توان کسری یا جذر متغیر دارد.
فرمولی که فقط جمع و تفریق اعداد و توانیهای x با ضرایب را شامل میشود.
فرمولی که همواره تقسیم متغیرها دارد و درجه متغیر نامحدود است.
تشخیص تابع چندجملهای بر اساس ظاهر فرمول آن و ساختار جملهها انجام میشود. در این نوع تابع، فرمول فقط از جمع و تفریق جملههایی با توانهای صحیح و غیرمنفی متغیر x و ضرایب عددی تشکیل شده است؛ هیچ ضرب یا تقسیم متغیرها، ریشه، جذر یا توابع مثلثاتی در ساختار آن وجود ندارد. آنچه از ترکیب جملههایی با ضرب، تقسیم یا چند نوع تابع دیگر ساخته شود، دیگر تابع چندجملهای نیست؛ مانند ترکیب با ریشه یا سینوس. بنابراین فقط عبارت «فرمولی که فقط جمع و تفریق اعداد و توانیهای x با ضرایب را شامل میشود» تعریف دقیق تابع چندجملهای را نشان میدهد.
۱۴. از روی نمودار تابع، چگونه میتوان صعودی یا نزولی بودن آن را تشخیص داد؟
اگر مقدار ورودی هر بار نصف شود و خروجی کمتر شود تابع نزولی و اگر بیشتر شود تابع صعودی است.
با شمارش تعداد نقاط برخورد نمودار با محور y مشخص میشود که تابع صعودی یا نزولی است.
اگر خروجی تابع همیشه برابر با مقدار ثابتی باشد تابع صعودی و اگر تغییر کند تابع نزولی است.
اگر با افزایش ورودی، نمودار از چپ به راست بالا برود تابع صعودی و اگر پایین بیاید تابع نزولی است.
وقتی نمودار تابع را مشاهده میکنیم، اگر با حرکت از چپ به راست مقدار خروجی زیاد شود و نمودار بالا برود، تابع صعودی نامیده میشود. برعکس، اگر نمودار به سمت پایین حرکت کند و خروجی کاهش یابد، تابع نزولی است. سایر جملات درباره ثابت بودن خروجی، شمارش نقطهها یا نصف کردن ورودی، ملاک تشخیص صعودی و نزولی بودن تابع از روی نمودار نیستند.
۱۵. در مثال محیط دایره، چرا رابطه بین شعاع و محیط یک تابع است؟
برای هر مقدار شعاع فقط یک محیط به دست میآید.
محیط و شعاع به هم وابسته ولی غیرمنحصر هستند.
امکان دارد دو شعاع متفاوت محیط برابر بسازند.
یک محیط خاص میتواند از چند شعاع حاصل شود.
رابطه بین شعاع و محیط دایره یک تابع است، زیرا هر مقدار مشخص شعاع دقیقا یک مقدار محیط را تعیین میکند و هیچ شعاعی وجود ندارد که دو مقدار محیط مختلف به آن ارتباط داده شود. بر خلاف گزینههای دیگر، در این رابطه برای یک محیط نمیتوان چند شعاع متفاوت یافت و هیچ دو شعاعی محیط یکسانی ایجاد نمیکنند. بنابراین ویژگی یکتایی خروجی برای هر ورودی برقرار است و این رابطه را به یک تابع تبدیل میکند.
۱۶. در تابع وارون، چه اتفاقی برای ورودی و خروجی رخ میدهد و این تغییر چه تاثیری بر نمودار تابع دارد؟
ورودی و خروجی با یکدیگر جابجا میشوند و نمودار نسبت به خط y=x قرینه میشود.
ورودی و خروجی همان حالت قبلی باقی میمانند و فقط مقدارها تغییر میکند.
تابع وارون ورودیها را منفی میکند و نمودار حول محور y محور میچرخد.
فقط ورودی تغییر میکند و خروجی ثابت است.
در تابع وارون، عمل جابجایی میان ورودی و خروجی اتفاق میافتد؛ یعنی مقدارهایی که قبلا ورودی تابع اصلی بودهاند خروجی وارون میشوند و برعکس. این جابجایی باعث میشود نمودار تابع وارون نسبت به خط y=x حالت قرینه پیدا کند. سایر گزینهها صحیح نیستند؛ زیرا تنها در وارون ورودی و خروجی جا عوض میکنند و نه فقط مقدار ورودی تغییر میکند، نه خروجی ثابت میماند و نه ورودیها صرفا منفی میشوند یا حول محور y میچرخند.













به نظرم کلا این پاراگراف را بازبینی کنید: «همانطور که مشاهده میکنید، رابطه بین مقادیر ورودی (برد) و خروجی (دامنه) در هر رابطه، با یک فلش نمایش داده شده است. بر اساس تعریف، اگر هر یک از مقادیر دامنه، تنها به یکی از مقادیر برد ارتباط داشته باشد، رابطه مورد نظر، یک تابع خواهد بود. در رابطه سمت راست، حروف m و n در برد، تنها به یکی از حروف q ،p یا r در دامنه ارتباط دارند. بنابراین، این رابطه، یک تابع را نمایش میدهد.»
با سلام خدمت شما؛
نکته بیان شده کاملا صحیح است و اصلاحات لازم در متن اعمال شد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
مثال 1 : تعیین تابع از روی رابطه : “اگر هر یک از مقادیر برد، تنها به یکی از مقادیر دامنه ارتباط داشته باشد، رابطه مورد نظر، یک تابع خواهد بود.” جای برد و دامنه رو عوض کنید.
با سلام و وقت بخیر؛
ممنون از توجه شما. متن اصلاح شد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
بسیاااااااااار عالیییییییییی
سلام بسیار عالی بود سپاسگزارم