اتحاد های مثلثاتی + اثبات اتحادها و نمونه سوال با جواب
در این آموزش از مجله فرادرس، با مهمترین اتحاد های مثلثاتی آشنا میشویم و علاوه بر بیان اثبات آنها، مثالهایی را نیز ارائه خواهیم کرد. برای دسترسی سریع به فرمولهای اتحادهای مثلثاتی، پیشنهاد میکنیم به بخش «خلاصه اتحاد های مثلثاتی» در انتهای این متن مراجعه کنید.
نسبتهای مثلثاتی
در این بخش، به معرفی نسبتهای مثلثاتی با استفاده از مثلث قائمالزاویه می پردازیم. شش نسبت مثلثاتی اصلی وجود دارد: سینوس، کسینوس، تانژانت، کتانژانت، سکانت و کسکانت. برای زوایای حاده، این نسبتها را میتوان بهعنوان نسبت بین اضلاع یک مثلث قائمالزاویه تعریف کرد.
مثلث قائمالزاویه ABC با زاویه حاده $$ A =\alpha$$ را در نظر بگیرید. ضلع $$b$$ بین زاویه $$\alpha$$ و زاویه قائمه $$ C$$ را ضلع مجاور به زاویه $$\alpha$$ مینامند. ضلع دیگر را ضلع مقابل زاویه $$\alpha$$ مینامند.
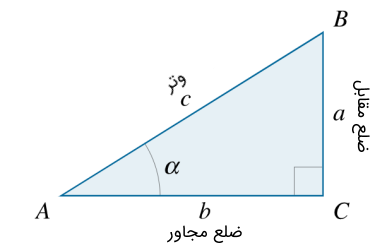
فرمول سینوس
سینوس زاویه $$ \alpha$$ را بهصورت $$ \sin \alpha $$ نشان میدهیم و بهصورت نسبت ضلع مقابل به وتر تعریف میکنیم:
$$ \large \boxed {\sin \alpha = \frac { a } { c } } $$
فرمول کسینوس
کسینوس زاویه $$ \alpha$$ را بهصورت $$ \cos \alpha $$ نشان میدهیم و بهصورت نسبت ضلع مجاور به وتر تعریف میکنیم:
$$ \large \boxed {\cos \alpha = \frac { b } { c } } $$
فرمول تانژانت
تانژانت زاویه $$ \alpha$$ را بهصورت $$ \tan \alpha $$ نشان میدهیم و بهصورت نسبت ضلع مقابل به ضلع مجاور تعریف میکنیم:
$$ \large \boxed {\tan \alpha = \frac { a } { b } } $$
تانژانت را می توان بر حسب سینوس و کسینوس بیان کرد:
$$ \tan \alpha = \frac { a } { b } = \frac { a } { c } \cdot \frac { c } { b } = \frac { { \frac { a } { c} } } { { \frac { b } { c } } } = \frac { { \sin \alpha } } { { \cos \alpha } } $$
$$ \large \boxed { \tan \alpha = \frac { { \sin \alpha } } { { \cos \alpha } } } $$
فرمول کتانژانت
نسبت متقابل تانژانت را کتانژانت میگویند و با $$ \cot \alpha $$ نشان میدهند. کتانژانت برابر با نسبت ضلع مجاور بر ضلع مقابل است:
$$ \large \boxed {\cot \alpha = \frac { b } { a } } $$
$$ \large \boxed { \cot \alpha = \frac { { 1 } } { { \tan \alpha } } } $$
کتانژانت را، مشابه تانژانت، میتوان برحسب سینوس و کسینوس نوشت:
$$ \large \boxed { \cot \alpha = \frac { { \cos \alpha } } { { \sin \alpha } } } $$
فرمول سکانت
نسبت اندازه وتر به اندازه ضلع مجاور را سکانت میگویند و با $$\sec \alpha $$ نشان میدهند:
$$ \large \boxed { \sec \alpha = \frac { { c } } { {b } } } $$
رابطه سکانت با کسینوس بهصورت زیر است:
$$ \large \boxed { \sec \alpha = \frac { { 1 } } { { \cos \alpha } } } $$

فرمول کسکانت
نسبت اندازه وتر به اندازه ضلع مقابل را کسکانت میگویند و با $$\csc \alpha $$ نشان میدهند:
$$ \large \boxed { \csc \alpha = \frac { { c } } { {a } } } $$
رابطه کسکانت با سینوس بهصورت زیر است:
$$ \large \boxed { \csc \alpha = \frac { { 1 } } { { \sin \alpha } } } $$
برای آشنایی بیشتر با نسبتهاب مثلثاتی، میتوانید به آموزشهای زیر مراجعه کنید:
- دایره مثلثاتی — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
- سینوس، کسینوس و تانژانت یک زاویه — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
- تانژانت و کتانژانت — نسبتهای مثلثاتی به زبان ساده (+ دانلود فیلم آموزش گام به گام)
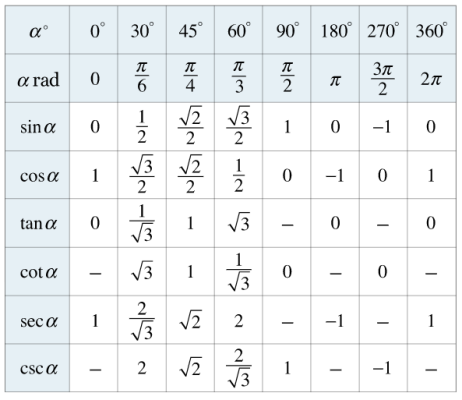
جدول نسبتهای مثلثاتی زاویههای مهم
جدول زیر، جدول نسبتهای مثلثاتی زاویههای مهم را نشان میدهد که بهتر است آنها را به خاطر بسپارید، زیرا در حل مسائل مختلف به آنها نیاز خواهید داشت:
اتحاد های مثلثاتی فیثاغورسی
اتحاد مثلثاتی یک تساوی شامل نسبتهای مثلثاتی است و برای همه مقادیر متغیری که هر دو طرف برابری برای آنها تعریف شده است صادق است. قضیه فیثاغورس را به یاد بیاورید که طول اضلاع یک مثلث قائمالزاویه را به هم مربوط میکند:
$${a^2} + {b^2} = {c^2} $$
همچنین، مثلث شکل زیر را در نظر بگیرید:
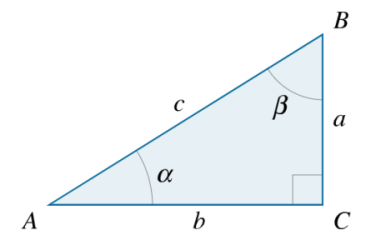
در بخش قبل دیدیم که رابطههای زیر را برای سینوس و کسینوس داریم:
$$ \sin \alpha = \frac{a}{c}\,\;\;cos \alpha = \frac{b}{c} $$
با به توان دو رساندن و جمع این معادلات به رابطه معروف زیر میرسیم:
$$ { \sin ^ 2 } \alpha + { \cos ^ 2 } \alpha = \frac { { { a ^ 2 } } }{ { { c ^ 2 } } } + \frac { { { b ^ 2 } } } { { { c ^ 2 } } } = \frac { { { a ^ 2 } + { b ^ 2 } } } { { { c ^ 2 } } } = \frac { { { c ^ 2 } } } { {{c^2}}} = 1$$
که به آن اتحاد مثلثاتی فیثاغورسی میگویند. بنابراین، برای هر زاویه $$ \alpha $$ در بازه $$ 0 \le \alpha \le \frac{\pi}{2} $$، میتوان نوشت:
$$ \large \boxed { {\sin ^2}\alpha + {\cos ^2}\alpha = 1} $$
با فرض $$ \cos \alpha \ne 0 $$ (یا همان $$ \alpha \ne \frac{\pi }{2} $$)، میتوانیم دو طرف اتحاد مثلثاتی فیثاغورسی را بر $$ {\cos^2}\alpha $$ تقسیم کنیم. در نتیجه، خواهیم داشت:
$$ require{cancel}\frac{{{{\sin }^2}\alpha }}{{{{\cos } ^ 2 } \alpha }} + \frac { cancel { { { \cos }^ 2 } \alpha }} { cancel { { { \cos } ^ 2 } \alpha }} = \frac { 1} {{ { { \cos } ^ 2 } \alpha }} $$
یا
$$ \large \boxed {\tan ^ 2 \alpha + 1 = \sec ^ 2 \alpha } $$
این اتحاد، تانژانت را به سکانت ربط میدهد.
بهطور مشابه، اگر $$ \sin \alpha \ne 0 $$، یعنی $$\alpha \ne 0$$، میتوانیم اتحاد مثلثاتی اولیه فیثاغورسی $${\sin^2}\alpha + {\cos^2}\alpha = 1 $$ را بر $${\sin^2}\alpha$$ تقسیم کنیم تا معادله مربوط به توابع کتانژانت و سکانت را بهدست آوریم:
$$ \frac { cancel { { { \sin } ^ 2 } \alpha } } { cancel { { { \sin } ^ 2 } \alpha } } + \frac { { { { \cos } ^ 2 } \alpha } }{ { { { \sin } ^ 2 }\alpha } } = \frac { 1 } { { { { \sin } ^ 2 } \alpha } } $$
یا
$$ \large \boxed { \cot ^ 2 \alpha + 1 = \csc ^ 2 \alpha } $$
به دو اتحاد اخیر نیز اتحادهای مثلثاتی فیثاغورسی نیز گفته میشود.
این اتحادها به ما کمک میکنند تا بین توابع مثلثاتی یک زاویه، بدون دانستن خود زاویه، تبدیلات را انجام دهیم و عبارات مثلثاتی را ساده کنیم.

مثال های اتحاد های مثلثاتی فیثاغورسی
در این بخش، چند مثال از کاربرد اتحاد های مثلثاتی فیثاغورسی را بررسی میکنیم.
مثال اول اتحاد های مثلثاتی فیثاغورسی
عبارت زیر را ساده کنید.
$$ \tan \alpha + \frac { { \cos \alpha } } { { 1 + \sin \alpha } } $$
حل: با استفاده از اتحاهای مثلثاتی فیثاغورسی، داریم:
$$ \begin {align}
\tan \alpha + \frac{{\cos \alpha } } { { 1 + \sin \alpha } } &\; = \frac { { \sin \alpha } } { { \cos \alpha } } + \frac { { \cos \alpha } } { { 1 + \sin \alpha }} = \frac { { \sin \alpha \left ( { 1 + \sin \alpha } \right ) + \cos \alpha \cos \alpha } } { { \cos \alpha \left ( { 1 + \sin \alpha } \right ) } } \ &\;= \frac{{\sin \alpha + \overbrace {{{\sin }^2}\alpha + {{\cos }^2}\alpha } ^ { = 1 } } } { { \cos \alpha \left( {1 + \sin \alpha } \right)}} = \frac{{\sin \alpha + 1 } } { { \cos \alpha \left ( { \sin \alpha + 1 } \right )} } = \frac { 1} { { \cos \alpha } } = \sec \alpha
\end {align} $$
مثال دوم اتحاد های مثلثاتی فیثاغورسی
اتحاد زیر را اثبات کنید.
$$ \frac { { { { \tan } ^ 2 } \alpha } } { { 1 + { { \tan } ^ 2 } \alpha } } \cdot \frac { { 1 + { { \cot } ^ 2 } \alpha } } { { { { \cot } ^ 2 } \alpha } } = { \tan ^ 2 } \alpha $$
حل: از اتحادهای فیثاغورسی استفاده میکنیم:
$$ \begin {align}
1 + { \tan ^ 2 } \alpha &\; = { \sec ^ 2 } \alpha = \frac { 1 } { { { { \cos } ^ 2 } \alpha } } \
1 + { \cot ^ 2 } \alpha &\; = { \csc ^ 2 } \alpha = \frac { 1 } { { { { \sin } ^ 2 } \alpha } }
\end {align} $$
سمت چپ تساوی اصلی بهصورت زیر است:
$$ \frac { { { { \tan } ^ 2 } \alpha } } { { \frac { 1 } { { { { \cos } ^ 2 } \alpha } } } } \cdot \frac { { \frac { 1 } { { { { \sin } ^ 2 } \alpha } } } } { { { { \cot } ^ 2 } \alpha } } = { \tan ^ 2 } \alpha $$
یا
$$ \frac { { { { \tan } ^ 2 } \alpha \, { { \cos } ^ 2 } \alpha } } { { { { \sin } ^ 2 } \alpha \, { { \cot } ^ 2 } \alpha } } = { \tan ^ 2 } \alpha $$
از آنجا که $$ { \cot ^ 2 } \alpha = \frac { { { { \cos } ^ 2 } \alpha } }{ { { { \sin } ^ 2 } \alpha } } $$، خواهیم داشت:
$$ require {cancel} \frac { { { { \tan } ^ 2 } \alpha cancel { { { \cot } ^ 2 } \alpha } } } { { cancel { { { \cot } ^ 2 } \alpha } } } = { \tan ^ 2 } \alpha \,\; \; \Rightarrow { \tan ^ 2 } \alpha = { \tan ^ 2 } \alpha $$
مثال سوم اتحاد های مثلثاتی فیثاغورسی
فرض کنید $$ \tan \alpha = \frac{2}{{15}}. $$. مقدار عددی عبارت زیر را محاسبه کنید.
$$ \frac { { 5 \sin \alpha + 6 \cos \alpha } } { { 4 \cos \alpha - 3 \sin \alpha } } $$
حل: از آنجا که $$ \tan \alpha $$ یک مقدار کراندار دارد، $$ \cos \alpha \ne 0 $$. بنابراین، میتوانیم صورت را بر مخرج تقسیم کنیم:
$$ \begin {align}
\frac{{5sin \alpha + 6cos \alpha }}{{4cos \alpha - 3sin \alpha }} &\; = \frac { { \frac { { 5 \sin \alpha + 6 \cos \alpha } }{ { \cos \alpha } } } } { { \frac { { 4 \cos \alpha - 3 \sin \alpha } } { { \cos \alpha } } } } = \frac { { \frac { { 5 \sin \alpha }} { { \cos \alpha } } + \frac { { 6 cancel { \cos \alpha } } }{ { cancel { \cos \alpha } } } } } { { \frac { { 4 cancel { \cos \alpha } } } { { cancel { \cos \alpha } } } - \frac { { 3 \sin \alpha } } { { \cos \alpha } } } } = \frac { { 5 \tan \alpha + 6 } } { { 4 - 3 \tan \alpha } } \ &\; = \frac { { 5 \times \frac { 2 } { { 1 5 } } + 6 } } { { 4 - 3 \times \frac { 2 } { { 1 5 } } } } = \frac { { \frac { 2 } { 3 } + 6 } } { { 4 - \frac { 2 } { 5 } } } = \frac { { \frac { { 2 + 1 8 } } {3 } } } { { \frac { { 2 0 - 2 } } { 5 } } } = \frac { { \frac { { 2 0 } } { 3 } } } { { \frac { { 1 8 } } { 5 } } } = \frac { { 1 0 0 } } { { 5 4 } } = \frac { { 5 0 } } { { 2 7 } }
\end {align} $$
مثال چهارم اتحاد های مثلثاتی فیثاغورسی
اگر $$ \sin \alpha + \cos \alpha = m $$، مقدار $$ {\sin ^4}\alpha + {\cos ^4}\alpha $$ را محاسبه کنید.
حل: هر دو طرف اتحاد مثلثاتی فیثاغورسی را به توان دو میرسانیم:
$$ { \sin ^ 2 } \alpha + { \cos ^ 2 } \alpha = 1 \, \
\Rightarrow { \left ( { { { \sin } ^ 2 } \alpha + { { \cos } ^ 2 } \alpha } \right ) ^ 2 } = 1 \, \ \Rightarrow { \sin ^ 4 } \alpha + 2 \, { \sin ^ 2 } \alpha \, { \cos ^ 2 } \alpha + { \cos ^ 4 } \alpha = 1 $$
بنابراین:
$$ { \sin ^ 4 } \alpha + { \cos ^ 4 } \alpha = 1 - 2 { \left ( { \sin \alpha \cos \alpha } \right ) ^ 2 } $$
اکنون $$ \sin \alpha \cos \alpha $$ را محاسبه میکنیم. طبق صورت سؤال، تساوی $$ \sin \alpha + \cos \alpha = m ~$$ را داریم. بنابراین، خواهیم داشت:
$$ \left ( { \sin \alpha + \cos \alpha } \right ) ^ 2 = { m ^ 2 } \, \; \; \Rightarrow { \sin ^ 2 } \alpha + 2 \sin \alpha \cos \alpha + { \cos ^ 2 } \alpha = { m ^ 2 } \, \;\; \ \Rightarrow 1 + 2 \sin \alpha \cos \alpha = { m ^ 2 } \, \;\; \Rightarrow \sin \alpha \cos \alpha = \frac { { { m ^ 2 } - 1 } } { 2 } $$
اتحاد های تناوب توابع مثلثاتی
همانطور که میدانیم توابع مثلثاتی متناوب هستند. با توجه به این دوره تناوب، میتوان اتحادهایی را برار توابع مثلثاتی بیان کرد.
دوره تناوب توابع سینوس و کسینوس $$ 2 \pi $$ است. اتحادهای زیر را برای این دو تابع داریم:
$$ \large \boxed {\cos \theta = \cos ( \theta + 2 \pi ) } $$
$$ \large \boxed {\sin \theta = \sin ( \theta + 2 \pi ) } $$
دوره تناوب توابع تانژانت و کتانژانت $$ \pi $$ است و برای این دو تابع، اتحادهای زیر را داریم:
$$ \large \boxed {\tan \theta = \tan ( \theta + \pi ) } $$
$$ \large \boxed {\cot \theta = \cot ( \theta + \pi ) } $$
همانطور که میدانیم، سکانت و کسکانت، بهترتیب، توابع معکوس کسینوس و سینوس هستند. بنابراین، دوره تناوب این توابع نیز $$ 2 \pi $$ است و برای آنها میتوان اتحادهای زیر را نوشت:
$$ \large \boxed {\sec \theta = \sec ( \theta + 2 \pi ) } $$
$$ \large \boxed {\csc \theta = \csc ( \theta + 2 \pi ) } $$
مثال های اتحاد های تناوب توابع مثلثاتی
در این بخش، چند مثال را از اتحادهای تناوب توابع مثلثاتی بررسی میکنیم.

مثال اول اتحاد های تناوب توابع مثلثاتی
حاصل عبارت زیر را محاسبه کنید:
$$ \frac { { \sin \left ( { - \frac { { 1 3 \pi } } { 2 } } \right ) + \tan \left ( { - 7 \pi } \right ) } } { { \cos \left ( { - 7 \pi } \right ) + \cot \left ( { - \frac { { 6 5 \pi } } { 4 } } \right ) } } $$
حل: هر جمله را جدا حساب میکنیم:
$$ \begin {align}
\sin \left ( { - \frac { {1 3 \pi } } { 2 } } \right ) &\; = \sin \left ( { \frac { { 3 \pi } } { 2 } - \frac { { 1 6 \pi } } { 2 } } \right ) = \sin \left ( { \frac { { 3 \pi } } { 2 } - 8 \pi } \right ) \ &\; = \sin \left ( { \frac { { 3 \pi } } { 2 } - 2 \pi \times 4 } \right ) = \sin \frac { { 3 \pi } } { 2 } = - 1\,
\end {align} $$
$$ \tan \left( { - 7 \pi } \right ) = \tan \left ( { 0 - \pi \times 7 } \right ) = \tan 0 = 0\, $$
$$ \cos \left ( { - 7 \pi } \right ) = \cos \left ( {\pi - 8 \pi } \right ) = \cos \left ( { \pi - 2 \pi \times 4 } \right ) = \cos \pi = - 1 \, $$
$$ \cot \left ( { - \frac { { 6 5 \pi } } { 4 } } \right ) = \cot \left ( { \frac { { 3 \pi } } { 4 } - \frac { { 6 8 \pi } } { 4 } } \right ) = \cot \left ( { \frac { { 3 \pi } } { 4} - 1 7 \pi } \right ) = \cot \frac { { 3 \pi } } { 4 } . $$
زاویه $$ \frac{{3pi }}{4} $$ در ربع دوم است که در آن کتانژانت منفی است. زاویه مرجع $$ \frac{{3pi }}{4} $$ برابر با $$\frac{{\pi }}{4} $$ است. بنابراین، داریم:
$$ \cot \left ( { - \frac { { 6 5 \pi } } { 4 } } \right ) = \cot \frac { { 3 \pi } } { 4 } = - \cot \frac { \pi } { 4 } = - 1 $$
در نتیجه:
$$ \frac { { \sin \left ( { - \frac { { 1 3 \pi } } { 2 } } \right ) + \tan \left ( { - 7 \pi } \right ) } } { { \cos \left ( { - 7 \pi } \right ) + \cot \left ( { - \frac { { 6 5 \pi } } { 4 } } \right ) } } = \frac { { - 1 + 0 } } { { - 1 - 1 } } = \frac { 1 } { 2 } $$
مثال دوم اتحاد های تناوب توابع مثلثاتی
عبارت زیر را ساده کنید:
$$ \frac { { \cos \left ( { - 3 \pi } \right ) + \sin { \frac { { 8 \pi }} {3 } } }} { {\tan { \frac { { 9 \pi } } { 4 } } + \cot { \frac { { 1 3 \pi } }{ 6 } } } } $$
حل: مقدار هر جمله را محاسبه میکنیم:
$$ \cos \left ( { - 3 \pi } \right ) = \cos \left ( { \pi - 4 \pi } \right ) = \cos \left ( { \pi - 2 \pi \times 2 } \right ) = \cos \pi = - 1 \, \
\sin \frac { { 8 \pi } } { 3 } = \sin \left ( { \frac { { 2 \pi } } { 3 } + \frac { { 6 \pi } } { 3 } } \right ) = \sin \left ( { \frac { { 2 \pi } } { 3 } + 2 \pi } \right ) = \sin \frac { { 2 \pi } } { 3 } . $$
زاویه مرجع $$ \frac{{2pi }}{3} $$، زاویه $$ \frac{{\pi }}{3} $$ است. بنابراین
$$ \sin \frac { { 8 \pi } } { 3 } = \sin \frac { { 2 \pi } } { 3 } = \sin \frac { \pi } { 3 } = \frac { { \sqrt 3 } } { 2 } $$
جملات دیگر نیز بهصورت زیر هستند:
$$ \tan \frac { { 9 \pi } } { 4 } = \tan \left ( { \frac { \pi } { 4 } + \frac { { 8 \pi } } { 4 } } \right ) = \tan \left ( { \frac { \pi }{ 4 } + 2 \pi } \right ) = \tan \frac { \pi } { 4 } = 1 \, \
\cot \frac { { 1 3 \pi } } { 6 } = \cot \left ( { \frac { \pi } { 6 } + \frac { { 1 2 \pi } } { 6 } } \right ) = \cot \left ( { \frac { \pi }{ 6 } + 2 \pi } \right ) = \cot \frac { \pi } { 6 } = \sqrt 3 . $$
با جایگذاری مقادیر، خواهیم داشت:
$$ \begin {align}
\frac { { \cos \left ( { - 3 \pi } \right ) + \sin \left ( { \frac { { 8 \pi } } {3 } } \right ) } } { { \tan \left ( { \frac { { 9 \pi } }{ 4 } } \right ) + \cot \left ( { \frac { { 1 3 \pi } } { 6 } } \right ) } } &\; = \frac { { - 1 + \frac { { \sqrt 3 } } { 2 } } } { { 1 + \sqrt 3 } } = \frac { { - 2 + \sqrt 3 } } { { 2 \left ( { 1 + \sqrt 3 } \right ) } } = \frac { { \left ( { - 2 + \sqrt 3 } \right ) \left ( { 1 - \sqrt 3 } \right ) } } { { 2 \left ( { 1 + \sqrt 3 } \right ) \left ( { 1 - \sqrt 3 } \right ) } } \ &\; = \frac { { - 2 + \sqrt 3 + 2 \sqrt 3 - 3 } } { { 2 \left ( { { 1 ^ 2 } - { { \left ( { \sqrt 3 } \right ) } ^ 2 } } \right ) } } = \frac { { 3 \sqrt 3 - 5 } } { { 2 \left ( { 1 - 3 } \right ) } } = \frac { { 5 - 3 \sqrt 3 } } { 4 } .
\end {align} $$

اتحاد های مثلثاتی جمع و تفریق دو زاویه
فرمولهایی وجود دارد که با کمک آنها میتوانیم جمع یا تفریق دو زاویه را ساده کنیم. در ادامه، با این فرمولها آشنا میشویم.
فرمول کسینوس تفریق دو زاویه
دو زاویه $$ \alpha $$ و $$ \beta $$ را با فرض $$ \alpha >\; \beta $$ در نظر بگیرید. نقاط $$A(o)$$ و $$M(\alpha)$$ و $$N(\beta)$$ و $$P(\alpha - \beta )$$ را روی دایره واحد مشخص میکنیم.
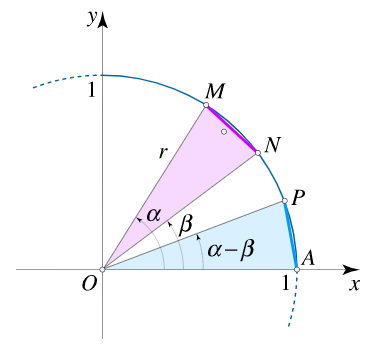
مختصات این نقاط بهصورت زیر هستند:
$$ \begin {align} &\; A = A \left( { 1 \, 0 } \right)\,\;\;M = M \left ( { \cos \alpha \, \sin \alpha } \right)\, \ &\; N = N \left ( { \cos \beta \,sin \beta } \right ) \, \; \; P = P \left ( { \cos \left ( { \alpha - \beta } \right ) \, \sin \left ( { \alpha - \beta } \right ) } \right)
\end {align} $$
از آنجا که $$\angle MON = \angle POA = \alpha - \beta$$، پارهخطهای $$\color{#cc00ff}{MN} $$ و $$\color{#0099ff}{AP}$$ طول یکسانی دارند:
$$\left| \color{#cc00ff}{MN} \right| = \left| \color{#0099ff}{AP} \right|. $$
فاصله بین دو نقطه روی یک صفحه با فرمول زیر بهدست میآید:
$$ d = \sqrt { { { \left( { { x _ 1 } - { x _ 2 } } \right ) } ^ 2 } + { { \left ( { { y _ 1 } - { y _ 2 } } \right ) } ^2 } } $$
بنابراین، خواهیم داشت:
$$\begin{align}
{ \left | \color{#cc00ff} { M N } \right | ^ 2 } &\; = { \left ( { { x _ M } - { x _ N } } \right ) ^ 2} + { \left ( { { y _ M } - { y _ N } } \right ) ^ 2 } = { \left ( { \cos \alpha - \cos \beta } \right ) ^ 2 } + { \left ( { \sin \alpha - \sin \beta } \right ) ^ 2 } \ &\; = { \cos ^ 2 } \alpha - 2 \cos \alpha \cos \beta + { \cos ^ 2 } \beta + { \sin ^ 2 } \alpha - 2 \sin \alpha \sin \beta + { \sin ^ 2 } \beta \ &\; = \underbrace { { { \cos } ^ 2 } \alpha + { { \sin } ^ 2 } \alpha } _ 1 + \underbrace { { { \cos } ^ 2 } \beta + { { \sin } ^ 2 } \beta } _ 1 - 2 \left ( { \cos \alpha \cos \beta + \sin \alpha \sin \beta } \right) \ &\; = 2 - 2 \left ( {\cos \alpha \cos \beta + \sin \alpha \sin \beta } \right)
\end {align}$$
بهطور مشابه، مجذور فاصله $$ \left| \color{#0099ff}{AP} \right| $$ بهصورت زیر خواهد بود:
$$\begin{align}
{ \left | \color {#0099ff} { A P } \right | ^ 2 } &\; = { \left ( { { x _ A } - { x _ P } } \right ) ^ 2 } + { \left ( { { y _ A } - { y _ P } } \right ) ^ 2 } = { \left ( { 1 - \cos \left ( { \alpha - \beta } \right ) } \right ) ^ 2 } + { \left ( { 0 - \sin \left ( { \alpha - \beta } \right ) } \right ) ^ 2 } \ &\; = 1 - 2 \cos \left ( { \alpha - \beta } \right ) + \underbrace { { { \cos } ^ 2 } \left ( { \alpha - \beta } \right) + { { \sin } ^ 2 } \left ( { \alpha - \beta } \right ) } _ 1 = 2 - 2 \cos \left ( { \alpha - \beta } \right )
\end {align}$$
فرمول کسینوس تفریق دو زاویه از تساوی $${\left| \color{#cc00ff}{MN} \right|^2} = {\left| \color{#0099ff}{AP} \right|^2}$$ بهصورت زیر بهدست میآید:
$$ \large \boxed { \cos ( \alpha – \beta ) = \cos \alpha \cos \beta + \sin \alpha \sin \beta } $$
فرمول کسینوس جمع دو زاویه
دو نقطه $$Nleft( \beta \right) $$ و $$Lleft( { - \beta } \right)$$ را در نظر بگیرید که، بهترتیب، روی تقاطع امتداد زاویههای $$ \beta$$ و $$ -beta$$ و محیط مربع قرار دارند.
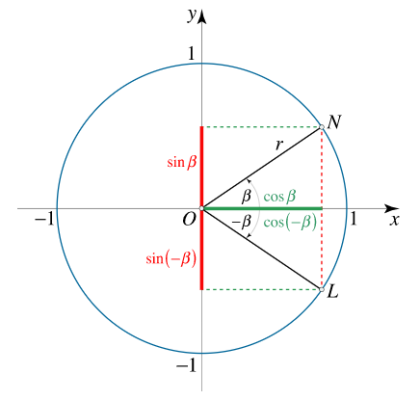
این نقاط نسبت به محور $$x$$ متقارن هستند. بنابراین مختصات افقی یکسانی دارند. قدر مطلق مختصات $$y$$ آنها مساوی است، اما در علامت مخالف هستند. به عبارت دیگر، تابع کسینوس زوج و تابع سینوس فرد است:
$$ \cos (-beta)=\cos \beta\, \quad \sin (-beta)=-sin \beta $$
اکنون از فرمول کسینوس تفریق دو زاویه استفاده میکنیم و بهجای $$\beta $$ از $$ -beta $$ استفاده میکنیم:
$$ \cos \left ( { \alpha + \beta } \right ) = \cos \alpha \cos \left ( { - \beta } \right ) + \sin \alpha \sin \left ( { - \beta } \right ) $$
از آنجا که کسینوس زوج است و سینوس فرد، آتحاد کسینوس جمع دو زاویه بهشکل زیر بهدست میآید:
$$ \large \boxed { \cos ( \alpha + \beta ) = \cos \alpha \cos \beta-sin \alpha \sin \beta } $$
حالتهای خاص
اگر از فرمولهای بالا استفاده کنیم، به روابطی بسیار کاربردی میرسیم. برای مثال، اگر $$\alpha = \frac{\pi }{2}$$ را در فرمول کسینوس تفریق دو زاویه قرار دهیم، خواهیم داشت:
$$ \cos \left ( { \frac { \pi } { 2 } - \beta } \right ) = \cos \frac { \pi } { 2 } \cos \beta + \sin \frac { \pi } { 2 } \sin \beta = 0 \cdot \cos \beta + 1 \cdot \sin \beta = \sin \beta $$
یا بهطور خلاصه، داریم:
$$ \large \boxed {\cos \left ( { \frac{ \pi }{2} - \beta } \right) = \sin \beta } $$
بهطور مشابه، فرمولهای زیر بهدست میآیند:
$$ \large \boxed {\sin \left ( { \frac{ \pi }{2} - \beta } \right) = \cos \beta } $$
$$ \large \boxed {\cos \left ( { \frac{ \pi }{2} + \beta } \right) = -sin \beta } $$
$$ \large \boxed {\sin \left ( { \frac{ \pi }{2} + \beta } \right) = \cos \beta } $$
فرمول سینوس تفریق دو زاویه
با استفاده از اتحادهای بخش قبل بخش قبل، فرمول تفریق سینوسی را به دست می آوریم:
$$ \large \boxed {\sin ( \alpha – \beta ) = \sin \alpha \cos \beta – \cos \alpha \sin \beta } $$

فرمول سینوس جمع دو زاویه
برای بهدست آوردن فرمول سینوس جمع دو زاویه، کافی است در فرمول بالا، بهجای $$\beta$$ مقدار $$-beta$$ را قرار دهیم:
$$ \begin {align} \sin \left( {\alpha + \beta } \right) &\; = \sin \alpha \cos \left( { - \beta } \right) - \cos \alpha \sin \left( { - \beta } \right) \ &\;= \sin \alpha \cos \beta + \cos \alpha \sin \beta \end {align} $$
بنابراین، میتوان نوشت:
$$ \large \boxed { \sin ( \alpha + \beta ) = \sin \alpha \cos \beta+cos \alpha \sin \beta } $$
برای آشنایی بیشتر با این دسته از اتحاد های مثلثاتی، به آموزش «سینوس و کسینوس جمع دو زاویه — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» مراجعه کنید.
فرمول تانژانت جمع دو زاویه
در بخشهای قبل با دو اتحاد زیر آشنا شدیم:
$$ \begin {align}
\sin \left( {\alpha + \beta } \right) &\; = \sin \alpha \cos \beta + \cos \alpha \sin \beta \
\cos \left( {\alpha + \beta } \right) &\; = \cos \alpha \cos \beta - \sin \alpha \sin \beta
\end {align} $$
فرض کنید $$\cos \left( {\alpha + \beta } \right) \ne 0$$ یا $$\alpha + \beta \ne \frac{\pi }{2} + \pi n\, n \in \mathbb{Z}$$. همچنین فرض کنید $$\cos \beta \ne 0$$ و $$\cos \beta \ne 0$$، که یعنی $$\alpha\, \beta \ne \frac{\pi }{2} + \pi n\,n \in \mathbb{Z}$$. بنابراین، میتوانیم دو تساوی اخیر را بر $$ cosalphacosbeta $$ تقسیم کنیم.
فرمول تانژانت جمع دو زاویه بهصورت زیر محاسبه میشود:
$$ require{cancel} \begin {align} \tan \left( {\alpha + \beta } \right) &\; = \frac{{\sin \left( {\alpha + \beta } \right)}}{{\cos \left( {\alpha + \beta } \right)}} = \frac{{\sin \alpha \cos \beta + \cos \alpha \sin \beta }}{{\cos \alpha \cos \beta - \sin \alpha \sin \beta }} \&\; = \frac{{\frac{{\sin \alpha \cos \beta + \cos \alpha \sin \beta }}{{\cos \alpha \cos \beta }}}}{{\frac{{\cos \alpha \cos \beta - \sin \alpha \sin \beta }}{{\cos \alpha \cos \beta }}}} = \frac{{\frac{{\sin \alpha cancel{\cos \beta} }}{{\cos \alpha cancel{\cos \beta} }} + \frac{{cancel{\cos \alpha} \sin \beta }}{{cancel{\cos \alpha} \cos \beta }}}}{{\frac{cancel{\cos \alpha \cos \beta }}{cancel{\cos \alpha \cos \beta }} - \frac{{\sin \alpha \sin \beta }}{{\cos \alpha \cos \beta }}}} \&\; = \frac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \tan \beta }} \end {align} $$
در نتیجه:
$$ \large \boxed { \begin {align} \tan \left( {\alpha + \beta } \right) = \frac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \tan \beta }} \end {align} } $$
فرمول تانژانت تفریق دو زاویه
میدانیم که تانژانت یک تابع فرد است:
$$ \tan \left( { - \beta } \right) = \frac{{\sin \left( { - \beta } \right)}}{{\cos \left( { - \beta } \right)}} = \frac{{ - \sin \beta }}{{\cos \beta }} = - \tan \beta $$
با قرار دادن $$ -beta $$ بهجای $$\beta $$ در فرمول تانژانت جمع دو زاویه، فرمول زیر برای تانژانت تفریق دو زاویه بهدست میآید:
$$ \tan \left ( { \alpha - \beta } \right ) = \frac { { \tan \alpha + \tan \left ( { - \beta } \right ) } } { { 1 - \tan \alpha \tan \left ( { - \beta } \right ) } } = \frac { { \tan \alpha - \tan \beta } } { { 1 + \tan \alpha \tan \beta } } $$
بنابراین، داریم:
$$ \large \boxed { \tan \left ( { \alpha - \beta } \right ) = = \frac { { \tan \alpha - \tan \beta } } { { 1 + \tan \alpha \tan \beta } }} $$
فرمول کتانژانت جمع دو زاویه
فرض کنید $$\sin \left( {\alpha + \beta } \right) \ne 0$$، که یعنی $$ \alpha + \beta \ne \pi n\,n \in \mathbb{Z} $$. همچنین، فرض کنید $$sinalpha \ne 0$$ و $$sinbeta \ne 0$$ یا $$\alpha \,beta \ne \pi n\,n \in \mathbb{Z}$$. بنابراین، میتوانیم عبارتی را که مینویسیم، بر $$sinalphasinbeta $$ تقسیم کنیم.
در نتیجه، خواهیم داشت:
$$ require {cancel}\begin {align}
\cot \left( {\alpha + \beta } \right) &\; = \frac{{\cos \left( {\alpha + \beta } \right)}}{{\sin \left( {\alpha + \beta } \right)}} = \frac{{\cos \alpha \cos \beta - \sin \alpha \sin \beta }}{{\sin \alpha \cos \beta + \cos \alpha \sin \beta }} \ &\; = \frac{{\frac{{\cos \alpha \cos \beta - \sin \alpha \sin \beta }}{{\sin \alpha \sin \beta }}}}{{\frac{{\sin \alpha \cos \beta + \cos \alpha \sin \beta }}{{\sin \alpha \sin \beta }}}} = \frac{{\frac{{\cos \alpha \cos \beta }}{{\sin \alpha \sin \beta }} - \frac{cancel{\sin \alpha \sin \beta }}{cancel{\sin \alpha \sin \beta }}}}{{\frac{{cancel{\sin \alpha} \cos \beta }}{{cancel{\sin \alpha} \sin \beta }} + \frac{{\cos \alpha cancel{\sin \beta} }}{{\sin \alpha cancel{\sin \beta} }}}} \ &\; = \frac{{\cot \alpha \cot \beta - 1}}{{\cot \beta + \cot \alpha }}
\end {align} $$
و میتوان نوشت:
$$\large \boxed {\begin {align}
\cot \left( {\alpha + \beta } \right) = \frac{{\cot \alpha \cot \beta - 1}}{{\cot \beta + \cot \alpha }}
\end {align}} $$
کتانژانت مجموع دو زاویه را میتوان برحسب تانژانتها نیز نوشت:
$$\large \boxed {
\cot ( \alpha + \beta ) = \frac { 1 - \tan \alpha \tan \beta } { \tan \alpha + \tan \beta }} $$
فرمول کتانژانت تفریق دو زاویه
میدانیم که کتانژانت یک تابع فرد است:
$$ \cot \left( { - \alpha } \right) = \frac{{\cos \left( { - \alpha } \right)}}{{\sin \left( { - \alpha } \right)}} = \frac{{\cos \alpha }}{{ - \sin \alpha }} = - \cot \alpha $$
اکنون با قرار دادن $$ -beta $$ بهجای $$ \beta $$ در فرمول کتانژانت جمع دو زاویه، میتوان نوشت:
$$ \cot \left ( { \alpha - \beta } \right ) = \frac { { \cot \alpha \cot \left ( { - \beta } \right ) - 1 } } { { \cot \alpha + \cot \left ( { - \beta } \right ) } } = \frac { { - \cot \alpha \cot \beta - 1 } } { { \cot \alpha - \cot \beta } } = \frac { { \cot \alpha \cot \beta + 1 } } { { \cot \beta - \cot \alpha } } $$
و خواهیم داشت:
$$ \large \boxed { \cot \left ( { \alpha - \beta } \right ) = \frac { { \cot \alpha \cot \beta + 1 } } { { \cot \beta - \cot \alpha } } } $$
این فرمول را برحسب تانژانت نیز میتوان نوشت:
$$\large \boxed {
\cot ( \alpha - \beta ) = \frac { 1 + \tan \alpha \tan \beta } { \tan \alpha - \tan \beta } } $$

کاربرد اتحاد های مثلثاتی جمع و تفریق دو زاویه
یکی از کاربردهای ساده اتحاد های مثلثاتی جمع و تفریق دو زاویه، سادهسازی عبارتهای مثلثاتی است که در حل مسائل مختلف با آنها سر و کار داریم. جدول زیر، مهمترین این فرمولها را نشان میدهد. اثبات این فرمولها را میتوانید با استفاده از آنچه در بخشهای قبل گفتیم، انجام دهید.
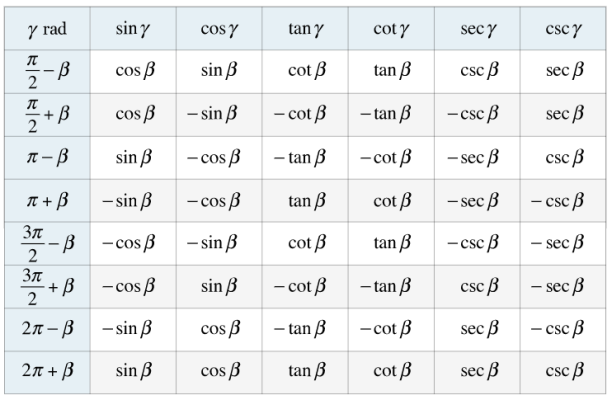
مثال های اتحاد های مثلثاتی جمع و تفریق دو زاویه
در این بخش، مثالهایی را از اتحاد های مثلثاتی جمع و تفریق دو زاویه بررسی میکنیم.
مثال اول اتحاد های مثلثاتی جمع و تفریق دو زاویه
مقدار عبارت $$ \cos \frac{{5pi }}{{12}} $$ را محاسبه کنید.
حل: عبارت $$ \frac{{5pi }}{{12}} $$ را بهصورت مجموع دو زاویه مینویسیم:
$$ \frac{{5pi }}{{12}} = \frac{{3pi + 2pi }}{{12}} = \frac{{3pi }}{{12}} + \frac{{2pi }}{{12}} = \frac{\pi }{4} + \frac{\pi }{6}. $$
با استفاده از فرمول کسینوس جمع، داریم:
$$ \begin {align}
\cos \frac { { 5 \pi } } { { 12 } } &\; = \cos \left ( { \frac { \pi }{4} + \frac { \pi } { 6 } } \right ) = \cos \frac{\pi }{4}\cos \frac{\pi }{6} - \sin \frac { \pi } { 4 } \sin \frac { \pi } { 6 } \ &\; = \frac { { \sqrt 2 } } { 2 } \cdot \frac { { \sqrt 3 } } { 2 } - \frac { { \sqrt 2 } } { 2 } \cdot \frac { 1 } { 2 } = \frac { { \sqrt 6 } } { 4 } - \frac { { \sqrt 2 } } { 4 } = \frac { { \sqrt 6 - \sqrt 2 } } { 4 } .
\end {align} $$
مثال دوم اتحاد های مثلثاتی جمع و تفریق دو زاویه
اگر مقدار $$ \sin \alpha = \frac{1}{{\sqrt 3 }} $$ را داشته باشیم، عبارت $$ \cos \left( {\frac{\pi }{3} + \alpha } \right) $$ را محاسبه کنید.
حل: تابع کسینوس در ربع اول مثبت است. بنابراین، خواهیم داشت:
$$ \cos \alpha = \sqrt { 1 - { { \sin } ^ 2 } \alpha } = \sqrt { 1 - { { \left ( { \frac { 1 } { { \sqrt 3 } } } \right ) } ^ 2 } } = \sqrt { 1 - \frac { 1 } { 3 } } = \sqrt { \frac { 2 } { 3 } } = \frac { { \sqrt 2 } } { { \sqrt 3 } } $$
اکنون از فرمول کسینوس جمع استفاده میکنیم:
$$ \begin {align}
\cos \left ( { \frac { \pi } { 3 } + \alpha } \right ) &\; = \cos \frac { \pi } { 3 } \cos \alpha - \sin \frac { \pi } { 3 } \sin \alpha \ &\; = \frac { 1 } { 2 } \cdot \frac { { \sqrt 2 } } { { \sqrt 3 } } - \frac { { \sqrt 3 } } { 2 } \cdot \frac { 1 } { { \sqrt 3 }} \ &\; = \frac{{\sqrt 2 - \sqrt 3 } } { { 2 \sqrt 3 } } = \frac { { \sqrt 6 - 3 } } { 6 }
\end {align} $$
میتوان گفت که کسینوس این زاویه منفی است.
مثال سوم اتحاد های مثلثاتی جمع و تفریق دو زاویه
اگر $$\cos \beta = -frac{1}{2}$$ و زاویه $$ \beta $$ در ربع دوم باشد، مقدار $$\sin \left( {\frac{\pi }{4} - \beta } \right) $$ را محاسبه کنید.
حل: سینوس در ربع دوم مثبت است. بنابراین، داریم:
$$ \sin \beta = \sqrt {1 - {{\cos } ^ 2 } \beta } = \sqrt { 1 - { { \left ( { - \frac { 1 } { 2 } } \right ) } ^ 2 } } = \sqrt { 1 - \frac { 1 } { 4 } } = \sqrt { \frac { 3 } { 4 } } = \frac { { \sqrt 3 } } { 2 } $$
با استفاده از سینوس جمع دو زاویه، میتوان نوشت:
$$ \begin {align} \sin \left ( { \frac { \pi } { 4 } - \beta } \right ) &\; = \sin \frac { \pi } { 4 } \cos \beta - \cos \frac { \pi } { 4 } \sin \beta \ &\; = \frac { { \sqrt 2 } } { 2 } \cdot \left ( { - \frac { 1 }{ 2 } } \right ) - \frac { { \sqrt 2 } } { 2 } \cdot \frac { { \sqrt 3 } } { 2 } \ &\; = \frac { {- \sqrt 2 - \sqrt 6 } } { 4 } \end {align} $$

مثال چهارم اتحاد های مثلثاتی جمع و تفریق دو زاویه
اتحاد $$ \cos \left( {\alpha + \beta } \right)\cos \left( {\alpha - \beta } \right)= {\cos ^2}\alpha - {\sin ^2}\beta $$ را ثابت کنید.
حل: با استفاده از اتحادهای کسینوس جمع و تفریق، سمت چپ تساوی را بازنویسی میکنیم:
$$ \begin{align} \cos \left( {\alpha + \beta } \right)\cos \left( {\alpha - \beta } \right) &\; = \left( {\cos \alpha \cos \beta - \sin \alpha \sin \beta } \right) \left( {\cos \alpha \cos \beta + \sin \alpha \sin \beta } \right) \&\; = {\cos ^2}\alpha \,{\cos ^2}\beta - {\sin ^2}\alpha\,{\sin ^2}\beta \end {align} $$
از تساویهای زیر استفاده میکنیم:
$$ {\cos ^2}\beta = 1 - {\sin ^2}\beta \;\;text{\,}\;\;{\sin ^2}\alpha = 1 - {\cos ^2}\alpha $$
و خواهیم داشت:
$$ \begin{align}
require{cancel} &\;{\cos ^2}\alpha \left( {1 - {{\sin }^2}\beta } \right) - \left( {1 - {{\cos }^2}\alpha } \right){\sin ^2}\beta \&\; = {\cos ^2}\alpha - cancel{{\cos ^2}\alpha \,{\sin ^2}\beta } - {\sin ^2}\beta + cancel{{\cos ^2}\alpha \,{\sin ^2}\beta} \ &\; = {\cos ^2}\alpha - {\sin ^2}\beta
\end {align} $$
مثال پنجم اتحاد های مثلثاتی جمع و تفریق دو زاویه
بیشترین و کمترین مقدار عبارت $$sinbeta - \sqrt{3}cosbeta $$ را محاسبه کنید.
حل: مقدار این عبارت را با $$ B$$ نشان میدهیم. بنابراین، میتوان نوشت:
$$ \begin{align}
\frac { B } { 2 } &\; = \frac { 1 } { 2 } \sin \beta - \frac { { \sqrt 3 } } { 2 } \cos \beta = \sin \frac { \pi } { 6 } \sin \beta - \cos \frac { \pi } { 6 } \cos \beta \ &\; = - \left ( { \cos \frac { \pi }{ 6 } \cos \beta - \sin \frac { \pi } { 6 } \sin \beta } \right ) = - \cos \left ( { \frac { \pi } { 6 } + \beta } \right)
\end {align} $$
بنابراین:
$$ B = - 2cos \left( {\frac{\pi }{6} + \beta } \right) $$
مثال ششم اتحاد های مثلثاتی جمع و تفریق دو زاویه
مقدار $$ \tan \frac{{5pi }}{{12}} $$ را محاسبه کنید.
حل: زاویه $$ \frac{{5pi }}{{12}} $$ را بهصورت مجموع دو زاویه مینویسیم که در جدول بالا وجود دارند و مقدار نسبتهای مثلثاتی آنها را میدانیم:
$$ \frac{{5pi } } { { 1 2 } } = \frac { { 3 \pi + 2 \pi } } { { 1 2 } } = \frac { { 3 \pi } } { { 1 2 } } + \frac { { 2 \pi } } { { 1 2 } } = \frac { \pi } { 4 } + \frac { \pi } { 6 } $$
اکنون، از اتحاد تانژانت جمع دو زاویه استفاده میکنیم:
$$ \begin {align} \tan \frac { { 5 \pi } } { { 1 2 } } &\; = \tan \left ( { \frac { \pi } { 4 } + \frac { \pi } { 6 } } \right ) = \frac { { \tan \frac { \pi } { 4 } + \tan \frac { \pi } { 6 } }} { { 1 - \tan \frac { \pi } { 4 } \tan \frac { \pi } { 6 } } } \ &\; = \frac { { 1 + \frac { 1 } { { \sqrt 3 } } } } { { 1 - 1 \cdot \frac { 1 }{ { \sqrt 3 } } } } = \frac { { \sqrt 3 + 1 } } { { \sqrt 3 - 1 } } = \frac { { { { \left ( { \sqrt 3 + 1 } \right ) } ^ 2 } } } { { \left ( { \sqrt 3 - 1 } \right ) \left ( { \sqrt 3 + 1 } \right ) } } \ &\;= \frac { { 3 + 2 \sqrt 3 + 1 } } { { 3 - 1 } } = \frac { { 4 + 2 \sqrt 3 } } { 2 } = 2 + \sqrt 3 \end {align} $$
مثال هفتم اتحاد های مثلثاتی جمع و تفریق دو زاویه
اگر $$ \cos \alpha = 0.6 $$ و زاویه $$\alpha $$ در ربع چهارم باشد، مقدار $$ \tan \left( {\frac{\pi }{3} + \alpha } \right) $$ را بهدست آورید.
حل: ابتدا مقدار $$ sinalpha $$ را با استفاده از اتحاد مثلثاتی فیثاغورسی بهدست میآوریم:
$$ \sin \alpha = - \sqrt {1 - {{\cos }^2}\alpha } = - \sqrt {1 - {{0.6}^2}} = - \sqrt {1 - 0.36} = - \sqrt {0.64} = - 0.8 $$
در نتیجه، تانژانت برابر است با
$$ \tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{ - 0.8}}{{0.6}} = - \frac{4}{3} $$
اکنون میتوانیم عبارت $$ \tan \left( {\frac{\pi }{3} + \alpha } \right) $$ را محاسبه کنیم:
$$ \begin {align} \tan \left ( { \frac { \pi } { 3 } + \alpha } \right ) &\; = \frac { { \tan \frac { \pi } { 3 } + \tan \alpha } } { { 1 - \tan \frac { \pi } { 3 } \tan \alpha } } = \frac { { \sqrt 3 - \frac { 4 } { 3 } } } { { 1 - \sqrt 3 \cdot \left ( { - \frac { 4 }{ 3 } } \right ) } } \ &\; = \frac { { 3 \sqrt 3 - 4 } } { { 4 \sqrt 3 + 3 } } = \frac { { \left ( { 3 \sqrt 3 - 4 } \right ) \left ( { 4 \sqrt 3 - 3 } \right ) } } { { \left ( { 4 \sqrt 3 + 3 } \right ) \left ( { 4 \sqrt 3 - 3 } \right ) } } \ &\; = \frac { { 3 6 - 1 6 \sqrt 3 - 9 \sqrt 3 + 1 2 } } { { 4 8 - 9 } } = \frac { { 4 8 - 2 5 \sqrt 3 } } { { 3 9 } } \end {align} $$
مثال هشتم اتحاد های مثلثاتی جمع و تفریق دو زاویه
عبارت زیر را ساده کنید:
$$ \frac{{2tan \alpha }}{{1 - {{\tan }^2}\alpha }}\cos 2alpha - \sin 2alpha $$
حل: میدانیم
$$ \frac{{2tan \alpha }}{{1 - {{\tan }^2}\alpha }} = \frac{{\tan \alpha + \tan \alpha }}{{1 - \tan \alpha \tan \alpha }} = \tan \left( {\alpha + \alpha } \right) = \tan 2alpha $$
در نتیجه، خواهیم داشت:
$$ \begin {align} require {cancel} \frac { { 2 \tan \alpha } } { { 1 - { { \tan } ^ 2 } \alpha } } \cos 2 \alpha - \sin 2 \alpha &\; = \tan 2 \alpha \cos 2 \alpha - \sin 2 \alpha \ &\; = \frac{{\sin 2alpha cancel{\cos 2alpha} }}{cancel{\cos 2alpha }} - \sin 2alpha \ &\;= \sin 2alpha - \sin 2alpha = 0 \end {align} $$

مثال نهم اتحاد های مثلثاتی جمع و تفریق دو زاویه
حاصل عبارت زیر را بهدست آورید:
$$ \frac{{{{\tan }^2}\frac{{7pi }}{{24}} - {{\tan }^2}\frac{\pi }{{24}}}}{{1 - {{\tan }^2}\frac{{7pi }}{{24}}\,{{\tan }^2}\frac{\pi }{{24}}}} $$
حل: از اتحاد مزدوج کمک میگیریم.
$$ {a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right) $$
با به کار بردن این اتحاد در صورت و مخرج عبارت و استفاده از فرمولهای تانژانت جمع و تانژانت تفریق دو زاویه، خواهیم داشت:
$$ \begin {align} \frac { { { { \tan } ^ 2 } \frac { { 7 \pi } }{ { 2 4 } } - { { \tan } ^ 2 } \frac { \pi } { { 2 4 } } } } { { 1 - { { \tan } ^ 2 } \frac { { 7 \pi } } { { 2 4 } } { { \tan } ^ 2 } \frac { \pi } { { 2 4 } } } } &\; = \frac { { \left ( { \tan \frac { { 7 \pi } } { { 2 4 } } - \tan \frac { \pi } { { 2 4 } } } \right ) \left ( { \tan \frac { { 7 \pi } } { { 2 4 } } + \tan \frac { \pi }{ { 2 4 } } } \right ) } } { { \left ( { 1 - \tan \frac { { 7 \pi } } { { 2 4 } } \tan \frac { \pi } { { 2 4 } } } \right ) \left ( { 1 + \tan \frac { { 7 \pi } } { { 2 4 } } \tan \frac { \pi } { { 2 4 } } } \right ) } } \ &\;= \frac { { \tan \frac { { 7 \pi } } { { 2 4 } } - \tan \frac { \pi } { { 2 4 } } } } { { 1 + \tan \frac { { 7 \pi } } { { 2 4 } } \tan \frac { \pi } { { 2 4 } } } } \cdot \frac { { \tan \frac { { 7 \pi } } { { 2 4 } } + \tan \frac { \pi }{ { 2 4 } } } } { { 1 - \tan \frac { { 7 \pi } } { { 2 4 } } \tan \frac { \pi } { { 2 4 } } } } \&\; = \tan \left ( { \frac { { 7 \pi } } { { 2 4 } } - \frac { \pi } { { 2 4 } } } \right ) \tan \left ( { \frac { { 7 \pi } } { { 2 4 } } + \frac { \pi } { { 2 4 } } } \right ) \&\; = \tan \frac { { 6 \pi } } { { 2 4 } } \tan \frac { { 8 \pi } } { { 2 4} } = \tan \frac { \pi } { 4 } \tan \frac { \pi } { 3 } = 1 \cdot \sqrt 3 = \sqrt 3 \end {align} $$
اتحاد های مثلثاتی دو برابر کمان
اتحادهای مثلثاتی دو برابر کمان را میتوان بهسادگی با توجه به آنچه برای نسبتهای مثلثاتی جمع دو زاویه گفتیم، بهدست آورد.
فرمول سینوس دو برابر کمان
برای بهدست آوردن فرمول سینوس دو برابر کمان، از فرمول سینوس جمع دو زاویه استفاده میکنیم:
$$ \sin \left ( { \alpha + \beta } \right) = \sin \alpha \cos \beta + \cos \alpha \sin \beta $$
با قرار دادن $$ \beta = \alpha $$ در فرمول بالا، خواهیم داشت:
$$ \sin \left ( { \alpha + \alpha } \right ) = \sin 2 \alpha = \sin \alpha \cos \alpha + \cos \alpha \sin \alpha = 2sin \alpha \cos \alpha $$
بنابراین، میتوان نوشت:
$$ \large \boxed {\sin {2 \alpha } = 2sin \alpha \cos \alpha } $$
فرمول کسینوس دو برابر کمان
مشابه آنچه برای سینوس گفتیم، از تساوی زیر استفاده میکنیم:
$$ \cos \left ( { \alpha + \beta } \right ) = \cos \alpha \cos \beta - \sin \alpha \sin \beta $$
با قرار دادن $$ \beta = \alpha $$ در فرمول کسینوس جمع، داریم:
$$ \cos \left ( { \alpha + \alpha } \right ) = \cos 2 \alpha = \cos \alpha \cos \alpha - \sin \alpha \sin \alpha = { \cos ^ 2 } \alpha - { \sin ^ 2 } \alpha $$
یا
$$ \large \boxed { \cos \left ( { 2alpha } \right ) = { \cos ^ 2 } \alpha - { \sin ^ 2 } \alpha } $$
اگر از تساوی $$ {\cos ^2}\alpha = 1 - {\sin ^2}\alpha $$ استفاده کنیم، فرمول اخیر را میتوان بهصورت زیر نوشت:
$$ \large \boxed { \cos 2alpha = 1 - 2 \, { \sin ^ 2 } \alpha } $$
یا با استفاده از تساوی $${\sin ^2}\alpha = 1 - {\cos ^2}\alpha $$ میتوان آن را بهصورت زیر نوشت:
$$ \large \boxed { \cos 2alpha= 2\,{\cos ^ 2 } \alpha - 1 } $$
فرمول تانژانت دو برابر کمان
برای بهدست آوردن فرمول تانژانت دو برابر کمان، از اتحاد تانژانت جمع دو زاویه استفاده میکنیم:
$$ \tan \left ( {\alpha + \beta } \right) = \frac{{\tan \alpha + \tan \beta } } { { 1 - \tan \alpha \tan \beta } } $$
با قرار دادن $$ \beta = \alpha$$، خواهیم داشت:
$$ \tan \left ( { \alpha + \alpha } \right ) = \tan 2 \alpha = \frac { { \tan \alpha + \tan \alpha } } { { 1 - \tan \alpha \tan \alpha } } = \frac { { 2 \tan \alpha } } { { 1 - { { \tan } ^ 2 } \alpha } } $$
یا
$$ \large \boxed {\tan { 2alpha } = \frac { { 2 \tan \alpha } } { { 1 - { { \tan } ^ 2 } \alpha } } } $$

فرمول کتانژانت دو برابر کمان
مشابه تانژانت، برای کتانژانت میتوان نوشت:
$$ \cot \left ( { \alpha + \beta } \right ) = \frac { { \cot \alpha \cot \beta - 1 } } { { \cot \alpha + \cot \beta } } \, \; \; \Rightarrow \cot 2 \alpha = \frac{{\cot \alpha \cot \alpha - 1}}{{\cot \alpha + \cot \alpha } } = \frac { { { { \cot } ^ 2 } \alpha - 1 } } { { 2 \cot \alpha } } $$
یا
$$ \large \boxed {\cot 2 \alpha = \frac { { { { \cot } ^ 2 } \alpha - 1 } } { { 2 \cot \alpha } }} $$
اتحاد های مثلثاتی سه برابر کمان
اتحاد های مثلثاتی سه برابر کمان، مشابه اتحاد های مثلثاتی دو برابر کمان محاسبه میشوند.
فرمول سینوس سه برابر کمان
مشابه فرمول سینوس دو برابر کمان، مینویسیم:
بنابراین، میتوان نوشت:
$$ \begin {align} \sin 3 \alpha &\; = \sin \left( {2alpha + \alpha } \right) = \sin 2alpha \cos \alpha + \cos 2alpha \sin \alpha \ &\;= 2sin \alpha \cos \alpha \cos \alpha + \left( {{{\cos }^2}\alpha - {{\sin }^2}\alpha } \right ) \sin \alpha \ &\; = 2 \sin \alpha \,{ \cos ^ 2 } \alpha + \left ( { 1 - 2 { { \sin } ^ 2 } \alpha } \right ) \sin \alpha \ &\; = 2 \sin \alpha \left ( { 1 - { { \sin } ^ 2 } \alpha } \right ) + \left ( { 1 - 2 \,{ { \sin } ^ 2 } \alpha } \right ) \sin \alpha \ &\; = 2sin \alpha - 2 \, { \sin ^ 3 } \alpha + \sin \alpha - 2 \, { \sin ^ 3 } \alpha = 3 \sin \alpha - 4 \, { \sin ^ 3 } \alpha \end {align} $$
در نتیجه، داریم:
$$ \large \boxed { \begin {align} \sin 3 \alpha = 3 \sin \alpha - 4 \, { \sin ^ 3 } \alpha \end {align} } $$
فرمول کسینوس سه برابر کمان
مشابه سینوس، فرمول کسینوس سه برابر کمان بهصورت زیر است:
$$ \large \boxed { \cos 3 \alpha = 4 \, { \cos ^ 3 } \alpha - 3 \cos \alpha } $$
فرمول تانژنت سه برابر کمان
با طی گامهایی مشابه بخشهای قبل، فرمول تانژنت سه برابر کمان بهصورت زیر است:
$$ \large \boxed { \tan 3 \alpha = \frac { { 3 \tan \alpha - { { \tan } ^ 3 } \alpha } } { { 1 - 3 \, { { \tan } ^ 2 } \alpha } } } $$
فرمول کتانژانت سه برابر کمان
فرمول کتانژانت سه برابر کمان بهصورت زیر است:
$$ \large \boxed { \cot 3 \alpha = \frac { { { { \cot } ^ 3 } \alpha - 3 \cot \alpha } } { { 3 \, { { \cot } ^ 2 } \alpha - 1 } } } $$
مثال های اتحاد های مثلثاتی چند برابر کمان
در این بخش، مثالهایی را از اتحاد های مثلثاتی دو برابر کمان و سه برابر کمان بررسی میکنیم.
مثال اول اتحاد های مثلثاتی چند برابر کمان
اگر $$ \tan \frac{\alpha}{2} = 3$$، آنگاه مقدار $$ \frac{{\cos \alpha }}{{2 - 3sin \alpha }} $$ را بیابید.
حل: از اتحادهای دو برابر کمان استفاده میکنیم:
$$ \cos \alpha = \frac { { 1 - { { \tan } ^ 2 } \frac { \alpha }{ 2 } } } { { 1 + { { \tan } ^ 2 } \frac { \alpha } { 2 } } } \, \; \; \sin \alpha = \frac { { 2 \tan \frac { \alpha } { 2 } } } { { 1 + { { \tan } ^ 2 } \frac{ \alpha } { 2 } } } $$
با قرار دادن این فرمولها در عبارت اصلی، خواهیم داشت:
$$ \begin {align} \frac { { \cos \alpha } } { { 2 - 3 \sin \alpha } } &\; = \frac{{\frac{{1 - {{\tan }^2}\frac{\alpha }{2}}}{{1 + {{\tan }^2}\frac{\alpha } { 2 } } } } } { { 2 - 3 \cdot \frac { { 2 \tan \frac { \alpha } { 2 } } } { { 1 + { { \tan } ^ 2 } \frac { \alpha } { 2 } } } } } = \frac { { \frac { { 1 - { { \tan } ^ 2 } \frac { \alpha } { 2 } } } { cancel { 1 + { { \tan } ^ 2 } \frac { \alpha } { 2 } }} } } { { \frac { { 2 \left ( { 1 + { { \tan } ^ 2 } \frac { \alpha } { 2 } } \right) - 6tan \frac { \alpha } { 2 } } } { cancel{1 + {{\tan }^2}\frac { \alpha } { 2 } } } } } \ &\;= \frac{{1 - {{\tan }^2}\frac{\alpha }{2}}}{{2 + 2\,{{\tan }^2}\frac{\alpha }{2} - 6tan \frac{\alpha }{2}}} = \frac{{1 - {3^2}}}{{2 + 2 \cdot {3^2} - 6 \cdot 3}} \ &\; = \frac{{1 - 9}}{{2 + cancel{18} - cancel{18}}} = \frac{{ - 8}}{2} = - 4 \end {align} $$

مثال دوم اتحاد های مثلثاتی چند برابر کمان
عبارت زیر را ساده کنید:
$$ \frac { { 1 + \sin 2 \alpha } } { { { { \left ( { \sin \alpha + \cos \alpha } \right ) } ^ 2 } } } $$
حل: با استفاده از فرمول سینوس دو برابر زاویه، خواهیم داشت:
$$ \begin {align} \frac { { 1 + \sin 2 \alpha } } { { { { \left ( {\sin \alpha + \cos \alpha } \right ) } ^ 2 }} } &\; = \frac { { 1 + \sin 2 \alpha } } { { { { \sin } ^ 2 } \alpha + 2 \sin \alpha \cos \alpha + {{\cos } ^ 2 } \alpha } } \&\;= \frac { { 1 + \sin 2alpha }}{{1 + 2sin \alpha \cos \alpha }} = \frac{cancel{1 + \sin 2alpha }}{cancel{1 + \sin 2alpha }} = 1 \end {align} $$
مثال سوم اتحاد های مثلثاتی چند برابر کمان
عبارت زیر را ساده کنید:
$$ \frac { { 2 \sin \beta - \sin 2beta } } { { 2sin \beta + \sin 2beta } } $$
با استفاده از فرمول سینوس و کسینوس دو برابر زاویه، خواهیم داشت:
$$ \begin {align}
\frac { { 2 \sin \beta - \sin 2 \beta } } { { 2 \sin \beta + \sin 2beta } } &\; = \frac{{2sin \beta - 2sin \beta \cos \beta }}{{2sin \beta + 2sin \beta \cos \beta }} = \frac{{cancel{2sin \beta} \left ( { 1 - \cos \beta } \right ) }} { { cancel { 2 \sin \beta } \left ( { 1 + \cos \beta } \right ) } } \ &\; = \frac { { 1 - \cos \beta } } { { 1 + \cos \beta } } = \frac { { 1 - { { \cos } ^ 2 } \frac { \beta }{ 2 } + { { \sin } ^ 2}\frac{\beta } { 2 } } } { { 1 + { { \cos } ^ 2 } \frac { \beta } { 2 } - { { \sin } ^ 2 } \frac { \beta } { 2 } } } = \frac { { { { \sin } ^ 2 } \frac { \beta } { 2 } + { { \sin } ^ 2 } \frac { \beta } { 2 } } } { { { { \cos } ^ 2 } \frac { \beta } { 2 } + { { \cos }^2}\frac{\beta }{2}}} \ &\;= \frac{{cancel{2}{{\sin }^2}\frac{\beta }{2}}}{{cancel{2}{{\cos }^2}\frac{\beta }{2}}} = {\tan ^2}\frac{\beta }{2}
\end {align}$$
مثال چهارم اتحاد های مثلثاتی چند برابر کمان
درستی تساوی زیر را بررسی کنید:
$$ \frac { { \sin 3 \alpha } } { { \sin \alpha } } - \frac { { \cos 3 \alpha } } { { \cos \alpha } } = 2 $$
حل: از فرمولهای سه برابر کمان استفاده میکنیم:
$$ \begin {align} \sin 3alpha &\; = 3sin \alpha - 4{\sin ^3}\alpha \
\cos 3alpha &\; = 4{\cos ^3}\alpha - 3cos \alpha \end {align} $$
سمت چپ عبارت دادهشده بهصورت زیر است و تساوی اثبات میشود:
$$ \begin {align}
\frac { { \sin 3 \alpha } } { { \sin \alpha } } - \frac { { \cos 3 \alpha } } { { \cos \alpha } } &\; = \frac{{3sin \alpha - 4\,{{\sin } ^ 3 } \alpha } } { { \sin \alpha } } - \frac { { 4 \, { { \cos } ^ 3 } \alpha - 3 \cos \alpha } } { { \cos \alpha }} \ &\;= \frac{{cancel{\sin \alpha} \left( {3 - 4\,{{\sin }^2}\alpha } \right)}}{{cancel { \sin \alpha} } } - \frac { { cancel { \cos \alpha} \left( {4\,{{\cos }^2}\alpha - 3} \right)}}{{cancel{\cos \alpha} }}\ &\; = 3 - 4\,{\sin ^2}\alpha - 4\,{\cos ^2}\alpha + 3 = 6 - 4left( {\underbrace {{{\sin }^2}\alpha + {{\cos }^2}\alpha }_1} \right) = 6 - 4 = 2.
\end {align} $$
مثال پنجم اتحاد های مثلثاتی چند برابر کمان
اگر $$ cotbeta = -3 $$، مقدار $$\sin 4beta $$ را محاسبه کنید.
حل: پیش از هر چیز، میدانیم:
$$ \tan \beta = \frac{1}{{\cot \beta }} = - \frac { 1 } { 3 } $$
با استفاده از فرمول سینوس دو برابر زاویه، میتوانیم بنویسیم:
$$ \sin 4beta = 2sin 2beta \cos 2beta $$
در ادامه، مقدار مورد نظر بهصورت زیر حاصل میشود:
$$ \begin {align} \sin 4 \beta &\; = 2 \sin 2 \beta \cos 2 \beta = 2 \cdot \frac { { 2 \tan \beta } } { { 1 + { { \tan } ^ 2 } \beta } } \cdot \frac { { 1 - { { \tan } ^ 2 } \beta } } { { 1 + { { \tan } ^ 2 } \beta } } \ &\;= 2 \cdot \frac { { 2 \cdot \left ( { - \frac { 1 } { 3 } } \right ) } } { { 1 + { { \left ( { - \frac { 1 } { 3 } } \right ) } ^ 2 } } } \cdot \frac { { 1 - { { \left ( { - \frac{1}{3}} \right)}^2}}}{{1 + {{\left( { - \frac{1}{3}} \right)}^2}}} = 2 \cdot \frac{{ - \frac{2}{3}}}{{1 + \frac{1}{9}}} \cdot \frac{{1 - \frac{1}{9}}}{{1 + \frac{1}{9}}} \ &\; = 2 \cdot \frac{{ - \frac{2}{3}}}{{\frac{{10}}{9}}} \cdot \frac{{\frac{8}{9}}}{{\frac{{10}}{9}}} = 2 \cdot \left( { - \frac { 6 } { { 1 0 } } } \right ) \cdot \frac { 8 } { { 1 0 } } = - \frac { { 9 6 } } { { 1 0 0 } } = - \frac { { 2 4 } } { { 2 5 } } \end {align} $$

اتحاد های مثلثاتی نصف کمان
در این بخش، اتحاد های مثلثاتی نصف کمان را معرفی میکنیم.
فرمول سینوس نصف کمان
همانطور که میدانیم، کسینوس دو برابر کمان بهصورت زیر است:
$$ \cos 2 \beta = 1 - 2\,{\sin ^2}\beta $$
این فرمول را بهصورت زیر مینویسیم:
$$ { \sin ^ 2 } \beta = \frac { { 1 - \cos 2beta } } { 2 } $$
با قرار دادن $$ \beta = \frac{\alpha }{2}$$، خواهیم داشت:
$$ { \sin ^ 2 } \frac { \alpha } { 2 } = \frac { { 1 - \cos \alpha }} { 2 } \, \; \; \Rightarrow \left| {\sin \frac{\alpha }{2}} \right| = \sqrt {\frac { { 1 - \cos \alpha } } { 2 } } \,\; \; \Rightarrow \sin \frac { \alpha } { 2 } = \pm \sqrt { \frac { { 1 - \cos \alpha } }{ 2 } } $$
بنابراین، میتوان نوشت:
$$\large \boxed { { \sin } \frac { \alpha } { 2 } = \pm \sqrt { \frac { { 1 - \cos \alpha } } { 2 } } } $$
علامت $$ \pm $$ در ابتدای سمت راست فرمول، نشان میدهد که ریشه مجذور، بسته به اینکه زاویه $$\frac \alpha 2 $$ در کدام ربع است، میتواند مثبت یا منفی باشد.
فرمول کسینوس نصف کمان
مشابه سینوس، برای کسینوس میتوان نوشت:
$$ \large \boxed { {\cos } \frac{\alpha } { 2 } = \pm \sqrt { \frac { { 1 + \cos \alpha } } { 2 } } } $$
فرمول تانژانت نصف کمان
برای محاسبه تانژانت نصف کمان، بهراحتی میتوان نوشت:
$$ { \tan ^ 2 } \frac { \alpha } { 2 } = \frac { { { { \sin } ^ 2 } \frac { \alpha } { 2 } } } { { { { \cos } ^ 2 } \frac { \alpha } { 2 } } } = \frac { { 1 - \cos \alpha } } { { 1 + \cos \alpha } } $$
در نتیجه، داریم:
$$ \large \boxed { \tan \frac { \alpha } { 2 } = \pm \sqrt { \frac { 1 - \cos \alpha } { 1 + \cos \alpha } } } $$
این فرمول را میتوانیم بهگونهای دیگر نیز بیان کنیم. فرمول زیر را میدانیم:
$$ \tan \frac { \alpha } { 2 } = \frac { { \sin \frac { \alpha }{2 } } } { { \cos \frac { \alpha } { 2 } } } $$
با ضرب صورت و مخرج کسر بالا در $$ {\cos \frac{\alpha }{2}} $$، داریم:
$$ \tan \frac { \alpha } { 2 } = \frac { { \sin \frac { \alpha } { 2 } } } { { \cos \frac { \alpha } { 2 } } } = \frac { { 2 \sin \frac { \alpha } { 2 } \cos \frac { \alpha } { 2 } } } { { 2 \cos \frac { \alpha } { 2 } \cos \frac { \alpha } { 2 } } } = \frac { { \sin \alpha } } { { 2 { { \cos }^ 2 } \frac { \alpha } { 2 } } } = \frac { { \sin \alpha } } { { 1 + \cos \alpha } } $$
بنابراین، میتوان نوشت:
$$ \large \boxed { \tan \frac { \alpha } { 2 } = \frac { { \sin \alpha } } { { 1 + \cos \alpha } } } $$
با طی گامهای مشابه، داریم:
$$ \tan \frac { \alpha } { 2 } = \frac { { \sin \frac { \alpha }{ 2 } } } { { \cos \frac { \alpha } { 2 } } } = \frac { { 2 \sin \frac { \alpha } { 2 } \sin \frac { \alpha } { 2 } } } { { 2 \sin \frac { \alpha } { 2 } \cos \frac { \alpha } { 2 } } } = \frac { { 2 { { \sin } ^ 2 } \frac { \alpha } { 2 } } } { { \sin \alpha } } = \frac { { 1 - \cos \alpha } } { { \sin \alpha } } $$
یا
$$ \large \boxed { \tan \frac { \alpha} { 2 } = \frac { 1 - \cos \alpha } { \sin \alpha } } $$
فرمول کتانژانت نصف کمان
فرمول ساده زیر را میدانیم:
$$ \cot \frac { \alpha } { 2 } = \frac { 1 } { { \tan \frac { \alpha } { 2 } } } $$
بنابراین، به توجه به فرمول تانژانت نصف کمان، فرمولهای زیر را برای کتانژانت داریم:
$$ \large \boxed { \cot \frac { \alpha } { 2 } = \frac { \sin \alpha } { 1 - \cos \alpha } } $$
$$ \large \boxed {\cot \frac{\alpha}{2}=\frac{1+cos \alpha}{\sin \alpha} } $$
مثال های اتحاد های مثلثاتی نصف کمان
در این بخش، چند مثال را بررسی میکنیم.
مثال اول اتحاد های مثلثاتی نصف کمان
عبارت زیر را ساده کنید:
$$ 2\,{\sin ^2}\frac{\alpha }{2} + \cos \alpha $$
حل: با استفاده از سینوس نصف کمان، داریم:
$$ require {cancel} 2\, { \sin ^ 2 } \frac { \alpha } { 2 } + \cos \alpha = 2 \cdot \frac { { 1 - \cos \alpha } } { 2 } + \cos \alpha = 1 - cancel { \cos \alpha } + cancel { \cos \alpha } = 1 $$
مثال دوم اتحاد های مثلثاتی نصف کمان
عبارت زیر را ساده کنید:
$$ \frac{{1 - \cos 2alpha }}{{\sin 2alpha }} $$
حل: با استفاده از اتحادهایی که یاد گرفتیم، میتون نوشت:
$$ require {cancel} \frac{{1 - \cos 2alpha }}{{\sin 2alpha }} = \frac{{cancel{2}\,{{\sin }^cancel{2}}\alpha }}{{cancel{2}cancel{\sin \alpha} \cos \alpha }} = \frac{{\sin \alpha }}{{\cos \alpha }} = \tan \alpha $$

مثال سوم اتحاد های مثلثاتی نصف کمان
عبارت زیر را ساده کنید:
$$ \frac{{1 - {{\tan }^2}\frac{\beta }{2}}}{{1 + {{\tan }^2}\frac{\beta }{2}}}$$
حل: از اتحاد تانژانت نصف کمان بهصورت زیر استفاده میکنیم:
$$ \tan \frac{\beta }{2} = \pm \sqrt {\frac{{1 - \cos \beta }}{{1 + \cos \beta }}} $$
در نتیجه، خواهیم داشت:
$$ \begin {align}
\frac { { 1 - { { \tan } ^ 2 } \frac{\beta } { 2 } }} { { 1 + { { \tan } ^ 2 } \frac{\beta } { 2 } } } &\; = \frac{{1 - \frac{{1 - \cos \beta }}{{1 + \cos \beta }}}}{{1 + \frac{{1 - \cos \beta }}{{1 + \cos \beta }}}} = \frac{{\frac{{1 + \cos \beta - \left( {1 - \cos \beta } \right)}}{{1 + \cos \beta }}}}{{\frac{{1 + \cos \beta + 1 - \cos \beta }}{{1 + \cos \beta }}}} \ &\; = \frac{{cancel{1} + \cos \beta - cancel{1} + \cos \beta }}{{1 + cancel{\cos \beta} + 1 - cancel{\cos \beta} }} = \frac{{cancel{2}\cos \beta }}{cancel{2}} = \cos \beta
\end {align} $$
مثال چهارم اتحاد های مثلثاتی نصف کمان
اتحاد زیر را اثبات کنید:
$$ 1 + \sin \beta = 2\,{\cos ^2}\left( {\frac{\pi }{4} - \frac{\beta }{2}} \right) $$
حل: از اتحاد کسینوس نصف کمان استفاده میکنیم:
$$ 2\,{\cos ^2}\frac{\theta }{2} = 1 + \cos \theta $$
تساوی زیر را نیز میدانیم:
$$ \cos \left( {\frac{\pi }{2} - \theta } \right) = \sin \theta $$
عبارت سمت راست تساوی صورت سؤال را بهشکل زیر مینویسیم:
$$ 2\,{\cos ^2}\left( {\frac{\pi }{4} - \frac{\beta }{2}} \right) = 1 + \cos \left( {\frac{\pi }{2} - \beta } \right) = 1 + \sin \beta $$
و میبینیم که با عبارت سمت چپ برابر است.
اتحاد های مثلثاتی تبدیل جمع به ضرب
در این بخش، با اتحاد های مثلثاتی تبدیل جمع و تفریق به ضرب آشنا میشویم.
اتحاد های مثلثاتی تبدیل جمع و تفریق سینوس به ضرب
در بخشهای قبل، با فرمول سینوس جمع و تفریق دو زاویه آشنا شدیم:
$$ \begin {align} \sin \left( {x + y} \right) &\; = \sin x \cos y + \cos x \sin y \
\sin \left( {x - y} \right) &\; = \sin x \cos y - \cos x \sin y
\end {align} $$
این دو معادله را با هم جمع و از هم کم میکنیم:
$$ \begin {align}
\sin \left( {x + y} \right) + \sin \left( {x - y} \right) &\; = 2sin x \cos y\
\sin \left( {x + y} \right) - \sin \left( {x - y} \right) &\; = 2cos x \sin y
\end {align} $$
تغیر متغیرهای $$ x + y = \alpha $$ و $$ x-y = \beta $$ را در نظر میگیریم. با توجه به این تساویها، خواهیم داشت:
$$ x = \frac{{\alpha + \beta }}{2}\,\;\;y = \frac{{\alpha - \beta }}{2} $$
اکنون عبارتهای اخیر را در فرمول جایگذاری میکنیم و به اتحادهای مهم زیر میرسیم:
$$ \large \boxed { \sin \alpha+sin \beta=2 \sin \frac{\alpha+beta}{2} \cos \frac{\alpha-beta}{2} } $$
$$ \large \boxed {\sin \alpha-sin \beta=2 \cos \frac{\alpha+beta}{2} \sin \frac{\alpha - \beta } { 2 } } $$
اتحاد های مثلثاتی تبدیل جمع و تفریق کسینوس به ضرب
مشابه روندی که برای تبدیل جمع و تفریق سینوس به ضرب طی کردیم، برای کسینوس به فرمولهای زیر میرسیم:
$$ \large \boxed { \cos \alpha+cos \beta=2 \cos \frac{\alpha+beta} { 2 } \cos \frac { \alpha - \beta } { 2 } } $$
$$ \large \boxed { \cos \alpha-cos \beta=-2 \sin \frac{\alpha+beta}{2} \sin \frac{\alpha-beta}{2} } $$
اتحاد های مثلثاتی تبدیل جمع و تفریق تانژانت به ضرب
جمع تانژانتهای دو زاویه را میتوان بهصورت زیر نوشت:
$$ \tan \alpha + \tan \beta = \frac{{\sin \alpha }}{{\cos \alpha }} + \frac { { \sin \beta } } { { \cos \beta } } = \frac{{\sin \alpha \cos \beta + \cos \alpha \sin \beta } } { { \cos \alpha \cos \beta } } $$
که با توجه به فرمول سینوس جمع زاویهها، بهصورت زیر درمیآید:
$$ \large \boxed { \tan \alpha+tan \beta=\frac{\sin (\alpha+beta)}{\cos \alpha \cos \beta} } $$
فرمول بالا در حالتی معتبر است که $$ cosalpha \ne 0 $$ و $$cosbeta \ne 0$$ برقرار باشد.
بهطور مشابه و با شرایطی که بیان شده، برای تفاضل تانژانتها، داریم:
$$ \large \boxed { \tan \alpha-tan \beta=\frac{\sin (\alpha-beta)}{\cos \alpha \cos \beta} } $$
اتحاد های مثلثاتی تبدیل جمع و تفریق کتانژانت به ضرب
مشابه آنچه برای تانژانتها گفتیم، فرمولهای زیر را با شروط $$ sinalpha \ne 0 $$ و $$ sinbeta \ne 0 $$ برای کتانژانتها داریم:
$$ \large \boxed { \cot \alpha+cot \beta=\frac{\sin (\alpha+beta)}{\sin \alpha \sin \beta} } $$
$$ \large \boxed { \cot \alpha-cot \beta=-frac{\sin (\alpha-beta)}{\sin \alpha \sin \beta} } $$

مثال های اتحاد های مثلثاتی تبدیل جمع به ضرب
در این بخش، چند مثال از مثال های اتحاد های مثلثاتی تبدیل جمع و تفریق به ضرب را حل میکنیم.
مثال اول اتحاد های مثلثاتی تبدیل جمع به ضرب
تساوی زیر را اثبات کنید:
$$ \cos { 4 7 ^ \circ } + \cos { 7 3 ^ \circ } = \cos { 1 3 ^ \circ} $$
حل: با استفاده از فرمول جمع کسینوس، داریم:
$$ \begin {align}
\cos { 4 7 ^ \circ } + \cos { 7 3 ^ \circ } &\; = 2 \cos \frac { { { { 4 7 } ^ \circ } + { { 7 3 } ^ \circ } } } { 2 } \cos \frac { { { { 4 7 } ^ \circ } - { { 7 3 } ^ \circ } } } { 2 } = 2 \cos \frac { { { { 12 0 } ^ \circ } } } { 2 } \cos \frac { { - { { 2 6 } ^ \circ } } } { 2 } \ &\; = 2 \cos { 6 0 ^ \circ } \cos \left ( { - { { 1 3 } ^ \circ } } \right ) = 2 \cdot \frac { 1 } { 2 } \cdot \cos \left ( { - { { 1 3 } ^ \circ } } \right ) = \cos \left ( { - { { 1 3 } ^ \circ } } \right )
\end {align} $$
میدانیم که تابع کسینوس زوج است. بنابراین، میتوانیم بنویسیم:
$$ \cos \left ( { - { { 1 3 } ^ \circ } } \right ) = \cos { 1 3 ^ \circ } $$
و اثبات کامل میشود.
مثال دوم اتحاد های مثلثاتی تبدیل جمع به ضرب
تساوی زیر را اثبات کنید:
$$ \begin {align}
\sin { 8 7 ^ \circ } - \sin { 2 7 ^ \circ } = \cos { 5 7 ^ \circ }
\end {align} $$
حل: با کمک اتحاد مثلثاتی تفاضل سینوسها، میتوانیم بنویسیم:
$$ \begin {align}
\sin { 8 7 ^ \circ } - \sin { 2 7 ^ \circ } &\; = 2 \cos \frac { { { { 8 7 } ^ \circ } + { { 2 7 } ^ \circ } } } { 2 } \sin \frac { { { { 8 7 } ^ \circ } - { { 2 7 } ^ \circ } } } { 2 } \ &\;= 2 \cos \frac { { { { 1 1 4 } ^ \circ} } } { 2 } \sin \frac { { { { 6 0 } ^ \circ } } } { 2} = 2 \cos { 57 ^ \circ } \sin { 3 0 ^ \circ } \ &\; = 2 \cdot \cos { 5 7 ^ \circ } \cdot \frac { 1 } { 2 } = \cos { 57 ^ \circ } \end {align} $$
مثال سوم اتحاد های مثلثاتی تبدیل جمع به ضرب
جمع زیر را به ضرب تبدیل کنید.
$$ \sin \beta + \cos 2 \beta - \sin 3 \beta $$
حل: با استفاده از فرمول تفاضل سینوسها، داریم:
$$ \begin {align}
\sin \beta + \cos 2 \beta - \sin 3 \beta &\; = \left ( { \sin \beta - \sin 3 \beta } \right ) + \cos 2 \beta \ &\; = 2 \cos \frac { { \beta + 3 \beta } } { 2 } \sin \frac { { \beta - 3 \beta } } { 2 } + \cos 2 \beta \ &\; = 2 \cos 2 \beta \sin \left ( { - \beta } \right ) + \cos 2 \beta \ &\; = \cos 2 \beta \left ( { 1 - 2 \sin \beta } \right )
\end {align} $$
مثال چهارم اتحاد های مثلثاتی تبدیل جمع به ضرب
عبارت زیر را ساده کنید:
$$ \frac { { \cos \alpha - \cos \beta } } { { \sin \alpha + \sin \beta } } $$
حل: با استفاده از اتحادهای جمع به ضرب، خواهیم داشت:
$$ require {cancel} \frac { { \cos \alpha - \cos \beta } } { { \sin \alpha + \sin \beta } } = \frac { { - cancel { 2 } cancel { \sin \frac { { \alpha + \beta } } { 2 } } \sin \frac { { \alpha - \beta } } { 2 } }} { { cancel { 2 } cancel { \sin \frac { { \alpha + \beta } } { 2 } } \cos \frac { { \alpha - \beta } } { 2 } } } = - \frac { { \sin \frac { { \alpha - \beta } } { 2 } } } { { \cos \frac { { \alpha - \beta } } { 2 } } } = - \tan \frac { { \alpha - \beta } } { 2 } $$
مثال پنجم اتحاد های مثلثاتی تبدیل جمع به ضرب
عبارت زیر را ساده کنید.
$$ \frac { { \sin 3 \alpha - \sin 7 \alpha } } { { \cos 4 \alpha + \cos 6 \alpha } } $$
حل: این عبارت را با $$ E $$ نشان میدهیم و از فرمولهای جمع به ضرب برای بازنویسی تفاضل سینوسها و جمع کسینوسها استفاده میکنیم:
$$ require {cancel} \begin {align}
E &\; = \frac { { \sin 3 \alpha - \sin 7 \alpha } } { { \cos 4 \alpha + \cos 6 \alpha } } = \frac { { cancel { 2 } \cos \frac { { 3 \alpha + 7 \alpha } } { 2 } \sin \frac { { 3 \alpha - 7 \alpha } } { 2 } } } { { cancel { 2 } \cos \frac { { 4 \alpha + 6 \alpha } } { 2 } \cos \frac { { 4 \alpha - 6 \alpha } } { 2 } } } \ &\; = \frac { { cancel { \cos 5 \alpha } \sin \left ( { - 2 \alpha } \right ) } } { { cancel { \cos 5 \alpha } \cos \left ( { - \alpha } \right ) } } = \frac { { \sin \left ( { - 2 \alpha } \right ) } } { { \cos \left ( { - \alpha } \right ) } }
\end {align} $$
تابع سینوس فرد و تابع کسینوس زوج است. از این رو، میتوان نوشت:
$$ E = \frac { { \sin \left ( { - 2 \alpha } \right ) } } { { \cos \left ( { - \alpha } \right ) } } = - \frac { { \sin 2 \alpha } } { { \cos \alpha } } $$
با استفاده از اتحاد سینوس دو برابر زاویه، داریم:
$$ E = - \frac { { \sin 2 \alpha } } { { \cos \alpha } } = - \frac { { 2 \sin \alpha cancel { \cos \alpha } } } { { cancel { \cos \alpha } } } = - 2 \sin \alpha $$

مثال ششم اتحاد های مثلثاتی تبدیل جمع به ضرب
تساوی زیر را اثبات کنید:
$$ \cos \frac { \pi } { 5 } + \cos \frac { { 3 \pi } } { 5 } = \frac { 1 }{ 2 } $$
حل: ابتدا مجموع کسینوسها را به یک حاصلضرب تبدیل میکنیم:
$$ \begin {align}
\cos \frac { \pi } { 5 } + \cos \frac { { 3 \pi } } { 5 } &\; = 2 \cos \frac { { \frac { \pi } { 5 } + \frac { { 3 \pi } }{ 5 } } } { 2 } \cos \frac { { \frac { \pi } { 5 } - \frac { { 3 \pi } } { 5 } } } { 2 } \ &\; = 2 \cos \frac { { 4 \pi } } { { 1 0 } } \cos \left ( { - \frac { { 2 \pi } } { { 1 0 } } } \right ) = 2 \cos \frac { { 2 \pi } } { 5 } \cos \frac { \pi } { 5 }
\end {align} $$
اکنون سمت چپ را در $$ \sin \frac{\pi }{5} $$ ضرب و بر آن تقسیم و سپس از اتحاد دو برابر زاویه برای سینوس استفاده میکنیم. بنابراین، سمت چپ تساوی صورت سؤال بهصورت زیر درمیآید:
$$ \begin {align}
\frac { { 2 \cos \frac { { 2 \pi } } { 5 } \cos \frac { \pi } { 5 } \sin \frac { \pi } { 5 } } } { { \sin \frac { \pi } { 5 } } } &\; = \frac { { \sin \frac { { 2 \pi } } { 5 } \cos \frac { { 2 \pi } }{ 5 } } } { { \sin \frac { \pi } { 5 } } } \ &\; = \frac { { 2 \sin \frac { { 2 \pi } } { 5 } \cos \frac { { 2 \pi } } { 5 } } } { { 2 \sin \frac { \pi } { 5 } } } = \frac { { \sin \frac { { 4 \pi } } { 5 } } } { { 2 \sin \frac { \pi } { 5 } } }
\end {align} $$
از فرمول زیر استفاده میکنیم:
$$ \sin \left ( { \pi - \alpha } \right ) = \sin \alpha $$
بنابراین، خواهیم داشت:
$$ require {cancel}\frac { { \sin \frac { { 4 \pi } } { 5 } } } { { 2 \sin \frac { \pi } { 5 } } } = \frac { { \sin \left ( { \pi - \frac { \pi } { 5 } } \right ) } } { { 2 \sin \frac { \pi } { 5 } } } = \frac { cancel { \sin \frac { \pi } { 5 } } } { { 2 cancel { \sin \frac { \pi } {5 } } } } = \frac { 1 } { 2 } $$
اتحاد های مثلثاتی تبدیل ضرب به جمع
در این بخش، با اتحاد های مثلثاتی تبدیل ضرب به جمع و تفریق آشنا میشویم.
اتحاد مثلثاتی تبدیل ضرب سینوس به جمع
فرمولهای زیر را از قبل میدانیم:
$$ \begin {align} \cos \left( {\alpha + \beta } \right) &\; = \cos \alpha \cos \beta - \sin \alpha \sin \beta \
\cos \left( {\alpha - \beta } \right) &\; = \cos \alpha \cos \beta + \sin \alpha \sin \beta
\end {align} $$
با کم کردن تساوی دوم از تساوی اول، خواهیم داشت:
$$ \cos \left( {\alpha + \beta } \right) - \cos \left( {\alpha - \beta } \right ) = - 2sin \alpha \sin \beta $$
بنابراین، فرمول تبدیل ضرب به جمع برای سینوس بهصورت زیر است:
$$ \large \boxed {
\sin \alpha \sin \beta=\frac{1}{2}[\cos (\alpha-beta)-cos (\alpha+beta)]} $$
اتحاد مثلثاتی تبدیل ضرب کسینوس به جمع
اگر اتحادهای مجموع و تفاضل بخش قبل را با هم جمع کنیم، خواهیم داشت:
$$ \cos \left( {\alpha - \beta } \right) + \cos \left( {\alpha + \beta } \right) = 2cos \alpha \cos \beta $$
در نتیجه، به فرمول زیر میرسیم:
$$ \large \boxed {
\cos \alpha \cos \beta=\frac{1}{2}[\cos (\alpha-beta)+cos (\alpha+beta)]} $$
اتحاد مثلثاتی تبدیل ضرب سینوس و کسینوس به جمع
به طور مشابه، میتوانیم حاصلضرب سینوس و کسینوس را بهصورت مجموع توابع مثلثاتی بیان کنیم. دو تساوی زیر را با هم جمع میکنیم:
$$ \begin {align} \sin \left( {\alpha + \beta } \right) &\; = \sin \alpha \cos \beta + \cos \alpha \sin \beta \
\sin \left( {\alpha - \beta } \right) &\; = \sin \alpha \cos \beta - \cos \alpha \sin \beta
\end {align} $$
و خواهیم داشت:
$$ \sin \left( {\alpha + \beta } \right) + \sin \left( {\alpha - \beta } \right) = 2sin \alpha \cos \beta $$
بنابراین، میتوان نوشت:
$$ \large \boxed { \sin \alpha \cos \beta=\frac{1}{2}[\sin (\alpha-beta)+sin (\alpha+beta)] } $$

اتحاد مثلثاتی تبدیل ضرب تانژانت به جمع
فرمولهای زیر را برای تانژانت و کتانژانت داریم:
$$ \begin {align} \tan \alpha + \tan \beta &\; = \frac{{\sin \left( {\alpha + \beta } \right)}}{{\cos \alpha \cos \beta }} \
\cot \alpha + \cot \beta &\; = \frac{{\sin \left( {\alpha + \beta } \right)}}{{\sin \alpha \sin \beta }}
\end {align} $$
دو اتحاد را بر هم تقسیم میکنیم:
$$ \begin {align}
require{cancel} \frac{{\tan \alpha + \tan \beta }}{{\cot \alpha + \cot \beta }} &\; = \frac{{\frac{{\sin \left( {\alpha + \beta } \right ) } } { { \cos \alpha \cos \beta }}}}{{\frac{{\sin \left( {\alpha + \beta } \right)}}{{\sin \alpha \sin \beta }}}} = \frac{{cancel { \sin \left( {\alpha + \beta } \right)} \cdot \sin \alpha \sin \beta }}{{\cos \alpha \cos \beta \cdot cancel{\sin \left( {\alpha + \beta } \right)}}} \ &\;= \frac{{\sin \alpha \sin \beta }}{{\cos \alpha \cos \beta }} = \tan \alpha \tan \beta
\end {align} $$
بنابراین، خواهیم داشت:
$$ \large \boxed { \tan \alpha \tan \beta=\frac{\tan \alpha+tan \beta}{\cot \alpha + \cot \beta } } $$
اتحاد مثلثاتی تبدیل ضرب کتانژانت به جمع
از آنجا که $$ \cot \theta = \frac{1}{{\tan \theta }} $$، میتوان نوشت:
$$ \cot \alpha \cot \beta = \frac{1}{{\tan \alpha \tan \beta }} = \frac{{\cot \alpha + \cot \beta } } { { \tan \alpha + \tan \beta } } $$
در نتیجه، داریم:
$$ \large \boxed { \cot \alpha \cot \beta = \frac{{\cot \alpha + \cot \beta } } { { \tan \alpha + \tan \beta } } } $$
اتحاد مثلثاتی تبدیل ضرب تانژانت در کتانژانت به جمع
از فرمول بخش قبل استفاده میکنیم و تغییر متغیر $$ \beta \to \frac{\pi }{2} - \beta $$ را بهکار میگیریم. تساویهای زیر را داریم:
$$ \tan \left( {\frac{\pi }{2} - \beta } \right) = \cot \beta\;\;text{\,}\;\;cot \left( {\frac{\pi }{2} - \beta } \right) = \tan \beta $$
بنابراین، میتوانیم بنویسیم:
$$ \tan \alpha \cot \beta = \tan \alpha \tan \left( {\frac{\pi }{2} - \beta } \right) = \frac{{\tan \alpha + \tan \left( {\frac{\pi }{2} - \beta } \right)}}{{\cot \alpha + \cot \left( {\frac{\pi }{2} - \beta } \right ) } } = \frac { { \tan \alpha + \cot \beta } } { { \cot \alpha + \tan \beta } } $$
در نتیجه:
$$ \large \boxed { \tan \alpha \cot \beta=\frac{\tan \alpha+cot \beta}{\cot \alpha + \tan \beta } } $$
مثال های اتحاد های مثلثاتی تبدیل ضرب به جمع
در این بخش، چند مثال را از اتحاد های مثلثاتی تبدیل ضرب به جمع بررسی میکنیم.
مثال اول اتحاد های مثلثاتی تبدیل ضرب به جمع
عبارت $$ \cos 4alpha \cos 6alpha $$ را بهصورت جمع توابع مثلثاتی نشان دهید.
حل: با استفاده از فرمولهای ضرب کسینوسها میتوان نوشت:
$$ \begin {align} \cos 4alpha \cos 6alpha &\; = \frac{1}{2}\left[ {\cos \left( {4alpha - 6alpha } \right) + \cos \left( {4alpha + 6alpha } \right)} \right] \ &\; = \frac{1}{2}\left[ {\cos \left( { - 2alpha } \right) + \cos 10alpha } \right] \ &\;= \frac{1}{2}\cos 2alpha + \frac{1}{2}\cos 10alpha \end {align} $$
مثال دوم اتحاد های مثلثاتی تبدیل ضرب به جمع
ضرب زیر را با جمع توابع مثلثاتی نشان دهید:
$$ \sin \alpha \sin 2alpha \sin 3alpha $$
حل: این عبارت را با $$ E$$ نشان میدهیم. ابتدا $$ sinalphasin 3alpha $$ را به جمع تبدیل میکنیم:
$$ \begin {align}
\sin \alpha \sin 3alpha &\; = \frac{1}{2}\left[ {\cos \left( {\alpha - 3alpha } \right) - \cos \left( {\alpha + 3alpha } \right)} \right] \ &\;= \frac{1}{2}\left[ {\cos \left( { - 2alpha } \right) - \cos 4alpha } \right] = \frac { 1 } { 2 } \left ( { \cos 2alpha - \cos 4alpha } \right)
\end {align} $$
سپس، عبارت اصلی را اینگونه مینویسیم:
$$ \begin {align}
E &\; = \sin \alpha \sin 2alpha \sin 3alpha = \sin 2alpha \cdot \frac { 1 } { 2 } \left ( { \cos 2alpha - \cos 4alpha } \right ) \ &\; = \frac { 1 } { 2} \sin 2alpha \cos 2alpha - \frac{1}{2}\sin 2alpha \cos 4 \alpha
\end {align} $$
داریم:
$$ \sin 2alpha \cos 2alpha = \frac{1}{2}\sin 4alpha $$
و
$$ \begin {align}
\sin 2alpha \cos 4alpha &\; = \frac{1}{2}\left[ {\sin \left( {2alpha - 4alpha } \right) + \sin \left( {2alpha + 4alpha } \right)} \right] \ &\;= \frac{1}{2}\left[ {\sin \left( { - 2alpha } \right) + \sin 6alpha } \right] = \frac{1}{2}\sin 6alpha - \frac{1}{2}\sin 2alpha
\end {align} $$
در نتیجه، حاصل عبارت بهصورت زیر خواهد بود:
$$ \begin {align}
E &\; = \frac{1}{2} \cdot \frac{1}{2}\sin 4alpha - \frac{1}{2} \left( {\frac { 1 } { 2 } \sin 6alpha - \frac{1}{2}\sin 2alpha } \right) \ &\; = \frac { 1 } { 4 } \sin 2alpha + \frac { 1 } { 4 } \sin 4 \alpha - \frac { 1 } { 4 } \sin 6 \alpha
\end {align} $$

مثال سوم اتحاد های مثلثاتی تبدیل ضرب به جمع
عبارت $$ 2sin 10^circ \cos 100^circ $$ را بهصورت جمع توابع مثلثاتی بنویسید.
حل: با استفاده از فرمولهایی که گفتیم، میتوانیم بنویسیم:
$$ \begin {align}
2 \sin {10 ^ \circ } \cos {100 ^ \circ} &\; = 2 \cdot \frac{1}{2}\left[ {\sin \left( {{{10}^circ} - {{100}^circ}} \right) + \sin \left( {{{10}^circ} + {{100}^circ}} \right)} \right] \ &\;= \sin \left( { - {{90}^circ}} \right) + \sin {110^circ}.
\end {align} $$
میدانیم:
$$ \sin \left( { - {{90}^circ}} \right) = - \sin {90^circ} = - 1\
\sin {110^circ} = \sin \left( {{{180}^circ} - {{110}^circ}} \right) = \sin {70^circ} $$
در نهایت، خواهیم داشت:
$$ 2sin {10^circ}\cos {100^circ} = \sin {70^circ} - 1 $$
مثال چهارم اتحاد های مثلثاتی تبدیل ضرب به جمع
ضرب زیر را به جمع تبدیل کنید:
$$ \cos \left ( {\alpha + \beta } \right ) \cos \left( {\alpha - \beta } \right ) $$
حل: از اتحاد ضرب کسینوسها استفاده میکنیم و خواهیم داشت:
$$ \begin {align}
\cos \left ( {\alpha + \beta } \right)\cos \left( {\alpha - \beta } \right) &\; = \frac{1}{2}\cos \left[ {\left( {\alpha - \beta } \right) - \left( {\alpha + \beta } \right)} \right] + \frac{1}{2}\cos \left[ {\left( {\alpha - \beta } \right) + \left( {\alpha + \beta } \right)} \right] \ &\;= \frac{1}{2}\cos \left( {cancel{\alpha} - \beta - cancel{\alpha} - \beta } \right) + \frac{1}{2}\cos \left( {\alpha - cancel{\beta} + \alpha + cancel{\beta} } \right) \ &\;= \frac{1}{2}\cos \left( { - 2beta } \right) + \frac{1}{2}\cos 2alpha = \frac{1}{2}\cos 2alpha + \frac{1}{2}\cos 2beta \end {align} $$
خلاصه اتحاد های مثلثاتی
در این آموزش، اتحادهای مثلثاتی را معرفی کردیم و علاوه بر روش بهدست آوردن آنها، مثالهای متنوعی را نیز بررسی کردیم. در این بخش، فهرستی خلاصه از مهمترین اتحادها را آوردهایم که میتوانید در صورت نیاز از آنها استفاده کنید.
نسبتهای مثلثاتی:
$$ \large \boxed { \begin {array} {\ll}
\tan \theta = \frac { \sin \theta } { \cos \theta } &\; \cot \theta = \frac { 1 } { \tan \theta } = \frac { \cos \theta } { \sin \theta } \
\sec \theta = \frac { 1 } { \cos \theta } &\; \csc \theta = \frac { 1 } { \sin \theta }
\end {array} } $$
اتحاد فیثاغورسی:
$$ \large \boxed {
\sin ^ { 2 } \theta + \cos ^ { 2 } \theta = 1
} $$
نسبتهای مثلثاتی متمم زاویه:
$$ \large \begin{array} {|ll|}
\hline \cos \theta = \sin \left ( \frac { \pi } { 2 } - \theta \right ) &\; \sin \theta = \cos \left ( \frac { \pi } { 2 } - \theta \right ) \
\cot \theta = \tan \left ( \frac { \pi } { 2 } - \theta \right ) &\; \tan \theta = \cot \left ( \frac { \pi } { 2 } - \theta \right ) \
\csc \theta = \sec \left ( \frac { \pi } { 2 } - \theta \right ) &\; \sec \theta = \csc \left ( \frac { \pi } { 2 } - \theta \right ) \
\hline
\end {array} $$
تناوب نسبتهای مثلثاتی:
$$\large \boxed { \begin {aligned}
\sin ( \theta + 2 \pi ) &\; = \sin \theta \
\cos ( \theta + 2 \pi ) &\; = \cos \theta \
\tan ( \theta + \pi ) &\; = \tan \theta \
\cot ( \theta + \pi ) &\; = \cot \theta
\end {aligned} }$$
نسبتهای مثلثاتی زاویه منفی:
$$ \large \boxed { \begin {aligned}
\sin ( - \theta ) &\; = - \sin \theta \
\cos ( - \theta ) &\; = \cos \theta \
\tan ( - \theta ) &\; = - \tan \theta \
\cot ( - \theta ) &\; = - \cot \theta \
\end {aligned} } $$
سینوس و کسینوس جمع و تفریق دو زاویه:
$$ \large \boxed { \begin {aligned}
&\; \sin ( \alpha + \beta ) = \sin \alpha \cos \beta+cos \alpha \sin \beta \
&\; \cos ( \alpha + \beta ) = \cos \alpha \cos \beta-sin \alpha \sin \beta \
&\; \sin ( \alpha - \beta ) = \sin \alpha \cos \beta - \cos \alpha \sin \beta \
&\; \cos ( \alpha - \beta ) = \cos \alpha \cos \beta + \sin \alpha \sin \beta
\end {aligned} } $$
سینوس دو برابر زاویه:
$$ \large \boxed { \sin 2 \theta = 2 \sin \theta \cos \theta } $$
کسینوس دو برابر زاویه:
$$ \large \boxed { \begin {aligned}
\cos 2 \theta &\; = \cos ^ { 2 } \theta - \sin ^ { 2 } \theta \
&\; = 2 \cos ^ { 2 } \theta - 1 \
&\; = 1 - 2 \sin ^ { 2 } \theta
\end {aligned} } $$
رابطه سکانت و تانژانت:
$$ \large \boxed { \sec ^ { 2 } \theta = 1 + \tan ^ { 2 } \theta } $$
نسبتهای مثلثاتی مکمل زاویه:
$$ \large \boxed { \begin {gathered}
\sin ( \pi - \theta ) = \sin \theta \
\cos ( \pi - \theta ) = - \cos \theta \
\tan ( \pi - \theta ) = - \tan \theta \
\cot ( \pi - \theta ) = - \cot \theta
\end {gathered} } $$
تانژانت جمع و تفریق و دو برابر زاویه:
$$ \large \boxed { \begin {aligned}
\tan 2 \theta &\; = \frac { 2 \tan \theta } { 1 - \tan ^ { 2 } \theta } \
\tan ( \alpha + \beta ) &\; = \frac { \tan \alpha + \tan \beta } { 1 -tan \alpha \tan \beta } \
\tan ( \alpha - \beta ) &\; = \frac { \tan \alpha - \tan \beta } { 1 + \tan \alpha \tan \beta }
\end {aligned} } $$
نسبتهای مثلثاتی نصف کمان:
$$ \large \boxed { \begin {aligned}
\sin \frac { \theta } { 2 } &\; = \pm \sqrt { \frac { 1 - \cos \theta } { 2 } } \
\cos \frac { \theta } { 2 } &\; = \pm \sqrt { \frac { 1 + \cos \theta } { 2 } } \
\tan \frac { \theta } { 2 } &\; = \frac { \sin \theta } { 1 + \cos \theta } = \frac { 1 - \cos \theta } { \sin \theta } \
\cot \frac { \theta } { 2 } &\; = \frac { 1 + \cos \theta } {\sin \theta} = \frac { \sin \theta } {1 - \cos \theta }
\end {aligned} } $$
تبدیل جمع و تفریق به ضرب:
$$ \large \boxed { \begin {aligned}
&\; \sin \alpha + \sin \beta = 2 \sin \frac { \alpha + \beta } { 2 } \cos \frac { \alpha - \beta } { 2 } \
&\; \cos \alpha + \cos \beta = 2 \cos \frac { \alpha + \beta } { 2 } \cos \frac { \alpha - \beta } { 2 } \
&\; \sin \alpha - \sin \beta = 2 \cos \frac { \alpha + \beta } { 2 } \sin \frac { \alpha - \beta } { 2 } \
&\; \cos \alpha - \cos \beta = - 2 \sin \frac { \alpha + \beta } { 2 } \sin \frac { \alpha - \beta } { 2 }
\end {aligned} } $$
تبدیل ضرب به جمع و تفریق:
$$ \large \boxed { \begin {aligned}
\sin \alpha \cos \beta &\; = \frac { \sin ( \alpha + \beta ) + \sin ( \alpha - \beta ) } { 2 } \
\cos \alpha \cos \beta &\; = \frac { \cos ( \alpha + \beta ) + \cos ( \alpha - \beta ) } { 2 } \
\sin \alpha \sin \beta &\; = \frac { \cos ( \alpha - \beta ) - \cos ( \alpha + \beta ) } { 2 }
\end {aligned} } $$
نسبتهای مثلثاتی سه برابر زاویه:
$$ \large \boxed { \begin {aligned}
\sin 3 \theta &\; = 3 \sin \theta - 4 \sin ^ { 3 } \theta \
\cos 3 \theta &\; = 4 \cos ^ { 3 } \theta - 3 \cos \theta \
\tan 3 \theta &\; = \frac { 3 \tan \theta - \tan ^ { 3 } \theta } { 1 - 3 \tan ^ { 2 } \theta } \
\cot 3 \theta &\;= \frac { { { { \cot } ^ 3 } \theta – 3 \cot \theta } } { { 3 \, { { \cot } ^ 2 } \theta – 1 } }
\end {aligned} } $$











با سلام خدمت گروه مجله فرادرس
مطالب بسیار عالی و کاربردی. اجرتون با حضرت
سلام ممنون از مقاله فوق العاده خوبتون
فقط تو مثال سوم اتحاد های مثلثاتی جمع و تفریق دو زاویه بخش آخر فکر کنم منفی به جای پشت کل کسر باید پشت رادیکال دو باشه که جواب کسر بشه منهای رادیکال دو منهای رادیکال شش تقسیم بر دو
با سلام؛
متن ویرایش شد،
با تشکر از همراهی شما با مجله فرادرس