معادله رادیکالی — به زبان ساده

در مطالب قبلی وبلاگ فرادرس معادله درجه دو و شیوه حل معادلات درجه سه به صورت دقیق مورد مطالعه قرار گرفتند ولی نحوه محاسبه پاسخ معادله رادیکالی همچنان به عنوان یک مسئله جدی باقی ماند. همچنین در مطلب «تغییر متغیر -- به زبان ساده» نشان داده شد که پاسخ یک معادله در حالتی که عبارت زیر رادیکال (رادیکال با فرجه زوج) مقداری منفی داشته باشد در محدوده اعداد مختلط قرار می‌گیرد. برای مثال نشان داده شد که پاسخ $$\surd{-1}$$ برابر با عدد موهومی i است.

این مطلب به صورت دقیق به مطالعه معادلات رادیکالی و شیوه حل آن‌ها می‌پردازد. در واقع نشان داده می‌شود که چه اقداماتی لازم است که هنگام مواجهه با معادلات رادیکالی با فرجه دو، سه و ... انجام شود. توجه کنید که رادیکال با فرجه دو را ریشه دوم و رادیکال با فرجه سه را ریشه سوم نیز می‌نامند. در انتهای مطلب شما قادر خواهید بود که پاسخ یک معادله شامل یک یا چند ترم رادیکالی را محاسبه کنید.

معادله رادیکالی چیست؟

همانطور که در ابتدای این مطلب اشاره شد، معادله رادیکالی معادله‌ای است که در آن یک یا چند ترم رادیکالی با فرجه دو، سه و ... حضور دارند. در واقع حل این معادلات یکی از چالش‌های اساسی در ریاضیات است و دانستن شیوه و الگوریتم محاسبه پاسخ آن‌ها، کمک بسیار زیادی به حل معادلات پیچیده‌تر نیز می‌کند.

فیلم آموزش ریاضی 2 – پایه یازدهم علوم تجربی در فرادرس

کلیک کنید

در ادامه این مطلب، به کمک چند مثال شیوه حل این نوع از معادلات به صورت دقیق شرح داده می‌شود.

حل معادلات رادیکالی

یکی از راه حل‌های کلی برای از بین بردن ریشه دوم (رادیکال با فرجه دو) این است که عبارت شامل ریشه دوم را به توان دو برسانیم. به شیوه مشابه می‌توان رادیکال با فرجه سه را به توان سه رساند و آن را از بین برد.

فیلم آموزش حسابان ۱ – پایه یازدهم – حل تمرین در فرادرس

کلیک کنید

نکته مهمی که در روند بالا باید به آن توجه کنید این است که، برخی از اوقات پاسخی که از روند بالا به دست می‌آید، در معادله اولیه صدق نمی‌کند. بنابراین این پاسخ، پاسخ صحیحی برای معادله رادیکالی مورد نظر ما نیست. بر این اساس باید دقت کنید که در انتهای راه حل، پاسخ به دست آمده را حتما در معادله اولیه قرار دهید و درستی آن را بررسی کنید.

به صورت کلی و با توجه به توضیحات ارائه شده می‌توان مراحل مختلف حل یک معادله رادیکالی را شامل دو مرحله دانست.

مرحله اول این است که ریشه دوم را در یک طرف معادله قرار دهیم و مرحله دوم برای حل معادله رادیکالی این است که هر دو طرف معادله به دست آمده را به توان دو (یا توان سه برای رادیکال با فرجه سه) برسانیم و در نهایت معادله به دست آمده را برای محاسبه مقدار مجهول، حل کنیم. این روند را می‌توان در مثال زیر به خوبی مشاهده کرد.

مثال

پاسخ صحیح معادله نشان داده شده در رابطه زیر را به دست آورید.

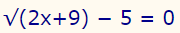
این مسئله در واقع به دنبال مقادیری از x است که در رابطه بالا صدق می‌کنند. بنابراین روندی که در درسنامه بالا توضیح داده شد را قدم به قدم طی می‌کنیم. همانطور که اشاره شد، مرحله اول این است که رادیکال را در یک سمت معادله و باقی اعداد و مجهولات را در سمت دیگر معادله قرار دهیم. بنابراین داریم:

مرحله دوم برای حل معادله رادیکالی فوق این است که طرفین معادله را به توان دو برسانیم. این مرحله در رابطه زیر اجرا شده است.

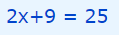
ادامه ماجرا بسیار ساده است و تنها نیاز به محاسبه مقدار x در معادله درجه یک بالا را داریم. برای این کار ابتدا 9 را به سمت راست معادله منتقل می‌کنیم.

سپس طرفین معادله به دست آمده را تقسیم بر دو می‌کنیم و در نهایت پاسخ مسئله محاسبه می‌شود. این روند با استفاده از روابط زیر به خوبی نشان داده شده است.

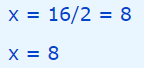
حال، باید یکی از مهم‌ترین مراحل برای حل یک معادله انتگرالی را طی کنیم. این مرحله قراردادن پاسخ در معادله اولیه و بررسی صحت آن است که این کار در رابطه زیر انجام شده است.

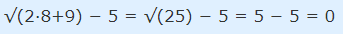
بنابراین مقدار x=8 را می‌توان به عنوان پاسخ صحیح مسئله، در نظر گرفت.

حل معادله رادیکالی با بیش از یک رادیکال

در بخش قبل به بیان مراحل مختلف برای حل معادله با یک عبارت رادیکالی پرداخته شد. اما شاید برای شما سوال پیش آمده باشد که اگر چند عبارت رادیکالی در مسئله موجود باشد، چگونه می‌توان مسئله مورد نظر را حل کرد. پاسخ بسیار ساده است. در واقع برای این حالت، مراحل بیان شده در بخش قبل را برای هرکدام از رادیکال‌ها تکرار می‌کنیم.

فیلم آموزش ریاضی و آمار 2 – پایه یازدهم علوم انسانی در فرادرس

کلیک کنید

بنابراین طبق روش توضیح داده شده، ممکن است زمان بسیار زیادی صرف محاسبه پاسخ مسئله شود ولی انجام این مراحل، کار سختی نیست و تنها عملی زمان‌بر است. البته نکته بسیار مهمی که باید به آن اشاره کرد این است که در این حالت نیز شما باید در انتهای حل، پاسخ معادله را در معادله ابتدایی قرار دهید و درستی پاسخ به دست آمده را بررسی کنید.

برای فهم دقیق شیوه انجام مراحل فوق به مثالی که در ادامه آورده شده، دقت کنید.

مثال

پاسخ معادله نشان داده شده در رابطه زیر را به دست آورید.

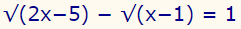
برای حل معادله فوق، ابتدا یکی از عبارات رادیکالی که ترم زیر رادیکال آن برابر با 2x-5 است را در سمت چپ معادله و باقی روابط را در سمت راست معادله قرار می‌دهیم. این موضوع در رابطه زیر به خوبی نشان داده شده است.

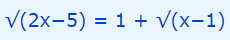
در ادامه، طرفین معادله فوق را به توان دو می‌رسانیم. بنابراین معادله به شکل زیر در می‌آید.

همانطور که مشاهده می‌شود، با انجام دو مرحله فوق، یکی از رادیکال‌ها از بین رفت و حال نوبت به از بین بردن رادیکال دوم است. بنابراین، حالت بسط داده شده سمت راست معادله فوق را به شکل زیر می‌نویسیم.

در ادامه، رابطه بالا را به فرم ساده شده زیر بیان می‌کنیم.

در این مرحله، از طرفین رابطه بالا، مقدار x را کم می‌کنیم و در نهایت این رابطه به شکل زیر در می‌آید.

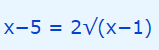
در ادامه و برای آنکه عبارت رادیکالی در یک سمت معادله باشد، کافی است طرفین معادله فوق را تقسیم بر دو کنیم. بنابراین رابطه بالا به شکل زیر در می‌آید.

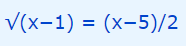
حال، طرفین رابطه فوق را به توان دو می‌رسانیم تا عبارت رادیکالی از بین برود.

بنابراین با استفاده از روندی که طی شد، دومین عبارت رادیکالی نیز از معادله صورت مسئله، حذف شد. بر این اساس و در ادامه، برای به دست آوردن x، ابتدا باید سمت راست معادله بالا را بسط دهیم. این موضوع در رابطه زیر نشان داده شده است.

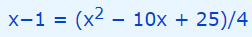
همانطور که مشاهده می‌شود این رابطه یک معادله درجه دو است که برای محاسبه پاسخ آن، کافی است که معادله را به فرم استاندارد معادلات درجه دو بازنویسی کنیم. بنابراین ابتدا عدد 4 را در طرفین رابطه فوق، ضرب می‌کنیم.

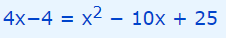
حال تمام عبارات را به سمت چپ معادله منتقل می‌کنیم. این موضوع در رابطه زیر به تصویر کشیده شده است.

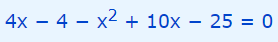
در ادامه رابطه بالا را ساده می‌کنیم.

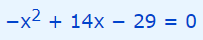
توجه کنید که ساده‌ترین حالت برای فرم استاندارد معادله درجه دو حالتی است که ضریب x² برابر با مقدار مثبت ۱ باشد. بنابراین طرفین رابطه بالا را در عبارت 1- ضرب می‌کنیم.

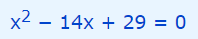
حال با استفاده از رابطه معروف معادلات درجه دو، پاسخ معادله فوق را محاسبه می‌کنیم. رابطه معادلات درجه دو به شکل زیر قابل بیان است.

فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد در فرادرس

کلیک کنید

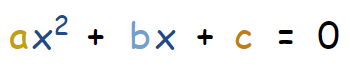
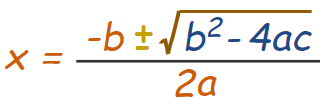
همانطور که مشاهده می‌شود، در رابطه این مسئله (x² - 14x + 29 = 0) مقدار b ،a و c به ترتیب برابر با 1، 14- و 29 هستند. بنابراین با جایگذاری مقادیر b ،a و c در رابطه فوق، پاسخ مسئله برابر با 2.53 و 11.47 خواهد بود.

توجه کنید که گام نهایی در حل این نوع از معادلات این است که پاسخ‌های به دست آمده را در معادله ابتدایی قرار دهیم و درستی آن‌ها را ارزیابی کنیم. بنابراین در ابتدا پاسخ x=2.53 را در معادله ابتدای مسئله قرار می‌دهیم.

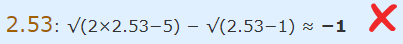
همانطور که مشاهده می‌شود با قرار دادن مقدار x=2.53 در معادله ابتدای مسئله، سمت راست معادله برابر با 1- شد که اشتباه است و باید برابر با 1+ باشد. بنابراین 2.53 پاسخ مسئله نیست. حال درستی مقدار x=11.47 را ارزیابی می‌کنیم.

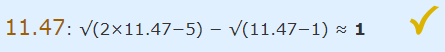
بنابراین همانطور که مشاهده می‌شود، مقدار x=11.47 تنها پاسخ این مسئله است.

نکته بسیار مهمی که در این مسئله نشان داده شد این است که روش ذکر شده ممکن است به پاسخ‌هایی برسد که واقعا پاسخ مسئله نباشند. بنابراین حتما باید در انتهای مسئله، پاسخ‌های به دست آمده را در رابطه صورت مسئله قرار دهیم و درستی آن‌ها را ارزیابی کنیم.

در صورتی که به مباحث مرتبط در زمینه ریاضیات پایه علاقه‌مند هستید، آموز‌ش‌های زیر به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• مجموعه آموزش‌های ریاضی و فیزیک
• مجموعه آموزش‌های دروس رسمی دبیرستان و پیش دانشگاهی
• اعداد گویا — به زبان ساده
• اعداد حقیقی — به زبان ساده
• اعداد مختلط – به زبان ساده
• ضرب متقاطع یا طرفین و وسطین — به زبان ساده

^^