مشتق توابع معکوس مثلثاتی — به زبان ساده

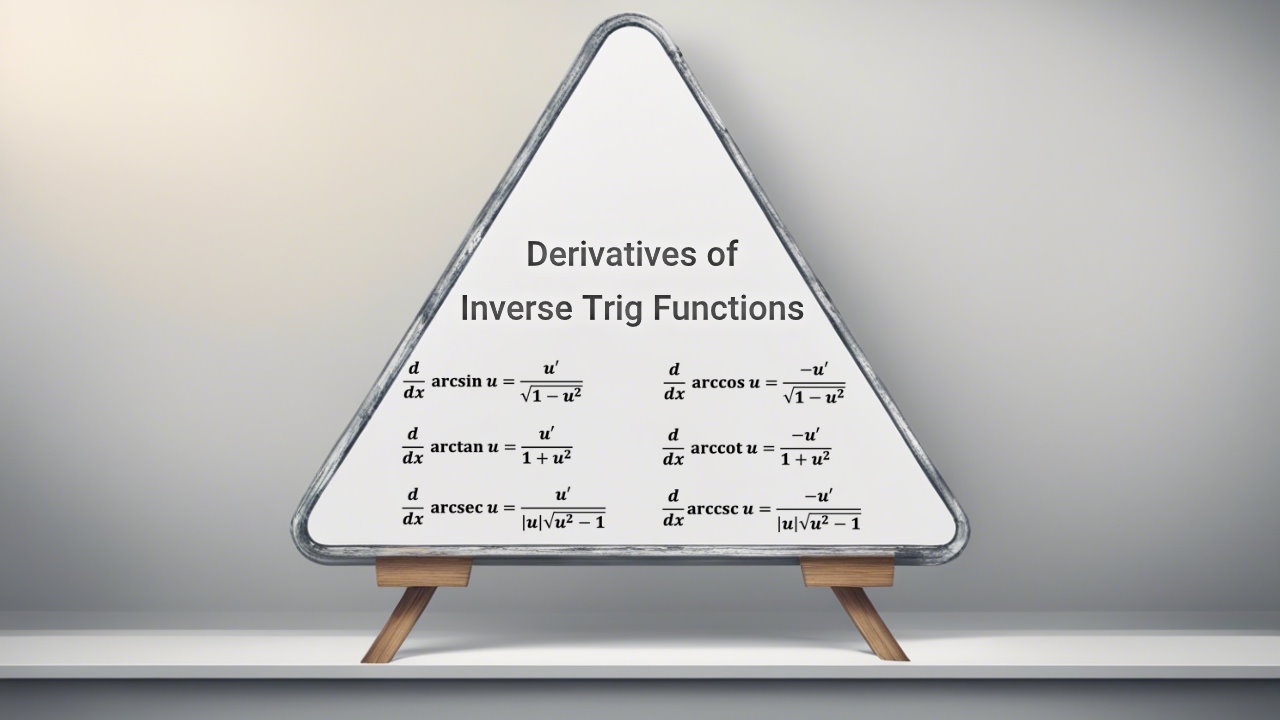
پیش‌تر در مطالب دایره مثلثاتی و سینوس، کسینوس و تانژانت یک زاویه، مفاهیم مرتبط با مثلثات را توضیح دادیم. در این قسمت، قصد داریم تا مشتق توابع معکوس مثلثاتی را ارائه دهیم. البته در صورتی که زمان کافی جهت مطالعه این مطلب ندارید، پیشنهاد می‌شود تا مطلب تقلب‌نامه مفاهیم و روابط مشتق را مطالعه فرمایید.

فرمول مشتق توابع معکوس

به منظور محاسبه مشتق توابع معکوس مثلثاتی ما نیاز داریم تا از رابطه‌ای استفاده کنیم که در بخش مشتق ضمنی ارائه شد. در مطلب مذکور رابطه‌ای عنوان شد که نحوه بدست آوردن مشتق معکوس یک تابع را بیان می‌کرد.

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

جهت یادآوری بایستی عنوان کنیم که اگر دو تابع (f(x و (g(x معکوس یکدیگر باشند، در این صورت رابطه‌ی زیر بین آن‌ها برقرار خواهد بود:

$$ \large g' \left ( x \right ) = \frac { 1 } { { f' \left ( { g \left ( x \right ) } \right ) } }$$

رابطه فوق از این مفهوم می‌آید که روابط $$  f \left ( { g \left ( x \right ) } \right ) = x $$ و $$ g \left ( { f \left ( x \right ) } \right ) = x $$ بین یک تابع و معکوسش برقرار هستند. در این قسمت مشتق توابع آرک سینوس، کسینوس و تانژانت را محاسبه کرده و مابقی را به خودتان واگذار می‌کنیم.

مشتق آرک سینوس

اجازه دهید نحوه بدست آوردن مشتق را با تابع آرک سینوس یا سینوس معکوس آغاز کنیم. تابع آرک سینوس به صورت زیر تعریف می‌شود.

$$ \large y = { \sin ^ { - 1 } } x \hspace {0.5in} \Leftrightarrow \hspace {0.5in} \sin y = x \hspace {0.25in} {\mbox{} }\,\,\,\,\,\,\,\,\,: \,\,\,\,\, - \frac { \pi } { 2 } \le y \le \frac { \pi } { 2 } $$

بنابراین تابع آرک سینوس ($$  y = { \sin ^ { - 1 } } x $$) معادل با این سوال است که به ازای قرار دادن چه زاویه‌ای (y) مقدار تابع سینوس برابر با x می‌شود. در رابطه فوق بازه‌ای برای y تعریف شده است. دلیل تعریف این بازه‌ این است که به ازای یک x ثابت می‌توان بینهایت مقدار برای y تعریف کرد.

توجه داشته باشید که با توجه به قرار داشتن تابع در بازه $$  - 1 < \sin ( y ) < + 1 $$ می‌توان نتیجه گرفت که x نیز بایستی در بازه $$  - 1 < x < + 1 $$ قرار داشته باشد. به‌ منظور درک مفهوم تابع آرک سینوس، به مثال زیر توجه فرمایید.

مثال ۱

مقدار تابع $$ \displaystyle { \sin ^ { - 1 } } \left ( { \frac { 1 } { 2 } } \right )$$ را بیابید.

پاسخ این مثال مقداری از y است که در رابطه $$ \sin \left ( y \right ) = \frac { 1 } { 2 } $$ صدق کند. البته همان‌طور که در بالا نیز عنوان شد این مقدار بایستی در بازه $$ - \frac { \pi } { 2 } \le y \le \frac { \pi } { 2 } $$ قرار داشته باشد. بدیهی است که مقدار $$ \sin \frac { \pi } { 6 } = \frac {1 } { 2 } $$ است، لذا پاسخ این سوال برابر با $$ y = \frac { \pi } { 6 } $$ است.

با توجه به مثال ارائه شده در بالا و مفاهیم تابع معکوس، رابطه زیر را می‌توان برای این تابع بیان کرد:

$$\large \sin \left ( { { { \sin } ^ { - 1 } } x } \right ) = x \enspace \enspace \ \ \Leftrightarrow \hspace { 0.5in } { \sin ^ { - 1 } } \left ( { \sin x } \right ) = x $$

با نامگذاری (f(x و (g(x به صورت زیر می‌توان مشتق تابع معکوس را نیز بدست آورد.

$$ \large f \left ( x \right ) = \sin x \hspace { 0.5in } g \left ( x \right ) = { \sin ^ { - 1 } } x $$

با استفاده از مفهوم مشتق‌ِ تابع معکوس، رابطه زیر بدست خواهد آمد.

$$\large g ^ { \prime } \left( x \right) = \frac{1}{{f ^ { \prime } \left ( { g \left ( x \right ) } \right ) } } = \frac { 1 } { { \cos \left ( { { { \sin } ^ { - 1 } } x } \right ) } } $$

رابطه ۱

عبارت فوق، نمی‌تواند رابطه مفیدی باشد. هنوز می‌توان آن‌ را ساده‌تر کرد. برای انجام این کار می‌توان از مفهوم تابع معکوس به صورت زیر استفاده کرد.

$$ \large y = { \sin ^ { - 1 } } \left ( x \right ) \hspace { 0.5in } \Rightarrow \hspace { 0.5in } x = \sin \left ( y \right ) $$

اگر از طرفین رابطه بالا cos گرفته شود، مخرجِ کسرِ ارائه شده در رابطه ۱ بدست خواهد آمد.

$$ \large \cos \left ( { { { \sin } ^ { - 1 } } x } \right ) = \cos \left ( y \right ) $$

می‌دانیم که $$ \cos y = \sqrt { 1 - { { \sin } ^ 2 } y } $$ است، لذا با جایگذاری آن در رابطه بالا داریم:

$$\large \cos \left ( { { { \sin } ^ { - 1 } } x } \right ) = \cos \left ( y \right ) = \sqrt { 1 - { { \sin } ^ 2 } y } $$

با جایگذاری $$ x = \sin y  $$ در رابطه بالا، داریم:

$$ \large \cos \left ( { { { \sin } ^ { - 1 } } x } \right ) = \sqrt { 1 - { { \sin } ^ 2 } y } = \sqrt { 1 - { x ^ 2 } } $$

در نتیجه مشتق تابع معکوس سینوس برابر است با:

$$\boxed { \large \frac { d } { { d x } } \left ( { { { \sin } ^ { - 1 } } x } \right ) = \frac { 1 } { { \sqrt { 1 - { x ^ 2 } } } } }$$

دقیقا مشتق تابعِ معکوسِ هر تابعی را می‌توان با استفاده از همین روش بدست آورد.

مشتق آرک کسینوس

تابع آرک کسینوس یا کسینوس معکوس به صورت زیر بیان می‌شود:

$$ \large y = { \cos ^ { - 1 } } x \hspace { 0.5in } \Leftrightarrow \hspace { 0.5in } \cos y = x \hspace { 0.25in } { \mbox { : } } \, \, \, \, \, \, \, \, \,0 \le y \le \pi $$

مشابه با تابع آرک سینوس، در این تابع نیز بازه‌ای برای خروجیِ y در نظر گرفته شده است.

فیلم آموزش ریاضی عمومی ۲ – مرور و حل تمرین در فرادرس

کلیک کنید

مثال ۲

مقدار تابع معکوسِ $$ \displaystyle { \cos ^ { - 1 } } \left ( { - \frac { { \sqrt 2 } } { 2 } } \right ) $$ را بیابید.

در ابتدا از خود سوال کنید کسینوس چه زاویه‌ای برابر با $$ { - \frac { { \sqrt 2 } } { 2 } } $$ می‌شود؟ می‌دانید که $$ \cos \frac { 3 \pi } { 4 } \ = { - \frac { { \sqrt 2 } } { 2 } } $$ است؛ لذا پاسخ سوال برابر با $$ y = \frac { 3 \pi } { 4 } $$ است.

در این حالت نیز برای بدست آوردن مشتق معکوس تابع، در ابتدا توابع f و g را به شکل زیر در نظر بگیرید.

$$\large f \left ( x \right ) = \cos x \hspace { 0.2in }  \hspace { 0.2in } g \left ( x \right ) = { \cos ^ { - 1 } } x $$

با مشتق‌گیری از طرفین رابطه بالا، عبارت زیر بدست خواهد آمد.

$$\large g ^ {\prime} \left( x \right) = \frac { 1 } { { f ^ { \prime } \left ( { g \left ( x \right ) } \right ) } } = \frac{1}{{ - \sin \left ( { { { \cos } ^ { - 1 } } x } \right) } } $$

روش بدست آوردن مخرج رابطه بالا نیز دقیقا مشابه با روشی است که برای مشتق‌گیری از تابع معکوس سینوس استفاده شده است. با استفاده از روش مذکور، مشتق تابع معکوس برابر با رابطه زیر بدست می‌آید.

$$ \large \frac { d } { { d x } } \left ( { { { \cos } ^ { - 1 } } x } \right ) = - \frac { 1 } { { \sqrt { 1 - { x ^ 2 } } } } $$

همان‌طور که از رابطه فوق بر می‌آید، تنها تفاوت میان مشتق معکوس تابع سینوس و کسینوس در علامت آن‌ها است. توجه داشته باشید که بدست آوردن مشتق معکوس تابع تانژانت، اندکی متفاوت است. در ادامه مشتق تانژانت را نیز بدست خواهیم آورد.

در صورت علاقه به یادگیری روش‌های تعیین مشتق توابع مختلف، مطالعه مطلب «فرمول‌های مشتق مهم + سوال با جواب و دانلود PDF» را به شما پیشنهاد می‌کنیم.

مشتق آرک تانژانت

در ادامه تعریف آرک تانژانت ارائه شده است.

$$ \large y = { \tan ^ { - 1 } } x \hspace { 0.5in } \Leftrightarrow \hspace { 0.5in } \tan y = x \hspace { 0.25in }{ \mbox { : } } \, \, \, \, \, \, \, \, \, - \frac { \pi } { 2 } < y < \frac { \pi } { 2 } $$

برای نمونه می‌دانیم که تانژانت زاویه ۴۵ درجه یا $$ \frac { \pi } { 4 } $$ برابر با ۱ است؛ بنابراین رابطه زیر را می‌توان بیان کرد:

$$\large { \tan ^ { - 1 } } 1 = \frac { \pi }{ 4 } $$

فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

حال مشابه با حالت‌ آرک سینوس و آرک کسینوس، به منظور یافتن مشتق تابع آرک تانژانت، در ابتدا f و g به صورت زیر تعریف می‌شوند.

$$ \large f \left ( x \right ) = \tan x \hspace { 0.5in } g \left ( x \right ) = { \tan ^ { - 1 } } x $$

با مشتق‌گیری از طرفین آن داریم:

$$ \large g ^ { \prime } \left ( x \right ) = \frac { 1 } { { f ^ { \prime } \left ( { g \left ( x \right ) } \right ) } } = \frac { 1 } { { { { \sec } ^ 2 } \left ( { { { \tan } ^ { - 1 } } x } \right ) } } $$

برای بدست آوردن مخرج عبارت فوق، می‌دانیم:

$$ \large y = { \tan ^ { - 1 } } x \hspace { 0.5in } \Rightarrow \hspace { 0.5in } \tan y = x $$

با گرفتن توان دوم سکانت از رابطه فوق داریم:

$$ \large { \sec ^ 2 } \left ( { { { \tan } ^ { - 1 } } x } \right ) = { \sec ^ 2 } y $$

حال رابطه زیر را در نظر بگیرید:

$$ \large { \cos ^ 2 } y + { \sin ^ 2 } y = 1 $$

با تقسیم کردن طرفین رابطه بالا به $$ \cos ^ 2 y $$ داریم:

$$\large 1 + { \tan ^ 2 } y = { \sec ^ 2 } y $$

بنابراین مخرج مد نظر برابر است با:

$$ \large { \sec ^ 2 } \left ( { { { \tan } ^ { - 1 } } x } \right ) = { \sec ^ 2 } y = 1 + { \tan ^ 2 } y $$

از طرفی با توجه رابطه $$ \tan y = x $$ رابطه فوق را می‌توان به صورت $$ { \sec ^ 2 } \left ( { { { \tan } ^ { - 1 } } x } \right ) = 1 + { \tan ^ 2 } y = 1 + { x ^ 2 } $$ بازنویسی کرد. بنابراین مشتق تابع آرک تانژانت برابر است با:

$$ \large \frac { d } { { d x } } \left ( { { { \tan } ^ { - 1 } } x } \right ) = \frac { 1 } { { 1 + { x ^ 2 } } } $$

 مشتق دیگر توابع معکوس مثلثاتی را نیز می‌توان با استفاده از روش‌های ارائه شده در بالا بدست آورد. اما سه مورد عنوان شده، بیشترین استفاده را دارند.

مثال ۳

مشتق توابع زیر را بدست آورید.

1. $$ f \left ( t \right ) = 4 { \cos ^ { - 1 } } \left ( t \right ) - 1 0 { \tan ^ { - 1 } } \left ( t \right ) $$
2. $$ y = \sqrt z \, { \sin ^ { - 1 } } \left ( z \right ) $$

در مورد تابع a، کافی است از آرک کسینوس و آرک تانژانت به صورت جداگانه مشتق گرفته شده و به صورت زیر نوشته شود. در نتیجه این کار داریم:

$$\large f ^ { \prime } \left ( t \right ) = - \frac { 4 } { { \sqrt { 1 - { t ^ 2 } } } } - \frac { { 1 0 } } { { 1 +
{ t ^ 2 } } } $$

مشتق تابع b را نیز می‌توان با استفاده از قانون مشتق ضرب توابع بدست آورد.

$$ \large y ^ {\prime} = \frac {1 } { 2 } { z ^ { - \frac { 1 } { 2 } } } { \sin ^ { - 1 } } \left ( z \right ) + \frac { { \sqrt z } } { { \sqrt { 1 - { z ^ 2 } } } } $$