اکسترمم محلی تابع — از صفر تا صد (+ دانلود فیلم آموزش رایگان)

پیش‌تر، در مجموعه‌ آموزش‌های ریاضی مجله فرادرس، با اکسترمم مطلق تابع و روش به دست آوردن آن آشنا شدیم. در این آموزش، با اکسترمم محلی تابع آشنا می‌شویم و چند مثال را درباره این موضوع حل خواهیم کرد.

تعریف ماکزیمم محلی و مینیمم محلی

فرض کنید تابع $$ y = f ( x ) $$ در همسایگی $$ \delta $$ از نقطه $$ x _ 0 $$ تعریف شده است ($$ \delta > 0 $$). تابع $$ f ( x ) $$ دارای یک ماکزیمم محلی (یا نسبی) در نقطه $$ x _ 0 $$ است اگر برای همه $$x \neq x _ 0 $$ متعلق به همسایگی $$ \left( {{x_0} – \delta ,{x_0} + \delta } \right) $$ نامساوی زیر برقرار باشد:

$$ \large f \left ( x \right ) \le f \left ( { { x _ 0 } } \right ) . $$

اگر این نامساوی برای همه نقاط $$ x \ne {x_0} $$ در همسایگی $$ x _ 0 $$ اکید باشد:

$$ \large f ( x ) < f  ( x _ 0 ) , $$

آنگاه $$ x _ 0 $$ یک نقطه ماکزیمم محلی اکید است.

به طور مشابه، فرض کنید تابع $$ y = f ( x ) $$ در همسایگی $$ \delta $$ از نقطه $$ x _ 0 $$ تعریف شده است ($$ \delta > 0 $$). تابع $$ f ( x ) $$ دارای یک مینیمم محلی (یا نسبی) در نقطه $$ x _ 0 $$ است اگر برای همه $$ x \neq x _ 0 $$ متعلق به همسایگی $$ \left( {{x_0} – \delta ,{x_0} + \delta } \right) $$ نامساوی زیر برقرار باشد:

$$ \large f \left ( x \right ) \ge f \left ( { { x _ 0 } } \right ) . $$

اگر این نامساوی برای همه نقاط $$ x \ne {x_0} $$ در همسایگی $$ x _ 0 $$ اکید باشد:

$$ \large f ( x ) > f  ( x _ 0 ) , $$

آنگاه $$ x _ 0 $$ یک نقطه مینیمم محلی اکید است.

مفاهیم ماکزیمم محلی و مینیمم محلی تحت عبارت عمومی اکسترمم محلی شناخته می‌شوند. واژه «محلی» اغلب برای سادگی حذف می‌شود.

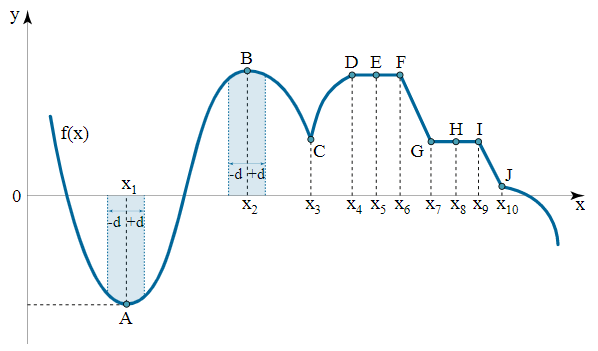
شکل ۱ نقاط اکسترمم مختلف را به صورت شماتیکی نشان می‌دهد. نقطه $$ A ( x _ 1 ) $$ یک نقطه مینیمم محلی اکید است، زیرا یک $$ \delta $$ در همسایگی $$\left( {{x_1} – \delta ,{x_1} + \delta } \right) $$ وجود دارد که در آن، نامساوی زیر برقرار است:

$$ \large { f \left ( x \right ) > f \left ( { { x _ 1 } } \right ) \; } \kern0pt { \forall \; x \in \left ( { { x _ 1 } – \delta , { x _ 1 } + \delta } \right ) . } $$

به طور مشابه، نقطه $$ B ( x _ 2 ) $$ یک نقطه ماکزیمم محلی اکید است. در این نقطه، نامساوی زیر را داریم:

$$ \large { f \left ( x \right ) < f \left ( { { x _ 2 } } \right ) \; } \kern0pt { \forall \; x \in \left ( { { x _ 2 } – \delta , { x _ 2 } + \delta } \right ) . } $$

درباره سایر نقاط نیز می‌توان موارد زیر را بیان کرد:

• $$ x _ 3 $$ یک نقطه مینیمم اکید است.
• $$ x _ 4 $$ یک نقطه ماکزیمم غیراکید است.
• $$ x _ 5 $$ یک نقطه ماکزیمم یا مینیمم غیراکید است.
• $$ x _ 6 $$ یک نقطه ماکزیمم غیراکید است.
• $$ x _ 7 $$ یک نقطه مینیمم غیراکید است.
• $$ x _ 8 $$ یک نقطه ماکزیمم یا مینیمم غیراکید است.
• $$ x _ 9 $$ یک نقطه ماکزیمم غیراکید است.
• $$ x _ {10} $$ اکسترمم نیست.

شرایط لازم و کافی وجود اکسترمم محلی

نقاطی که در آن‌ها مشتق تابع $$ f ( x ) $$ برابر با صفر است، نقاط مانا یا ثابت تابع نامیده می‌شوند. همچنین، نقاطی که در آن‌ها مشتق تابع $$ f ( x ) $$ برابر با صفر است یا در آن وجود ندارد، نقاط بحرانی تابع نامیده می‌شوند. در نتیجه، نقاط مانا زیرمجموعه نقاط بحرانی هستند.

یک شرط لازم برای وجود اکسترمم این‌گونه بیان می‌شود: اگر نقطه $$ x _ 0 $$ یک نقطه اکسترمم از تابع $$ f ( x ) $$ باشد، آنگاه مشتق در این نقطه یا صفر است یا وجود ندارد. به عبارت دیگر، اکسترمم‌های یک تابع از نقاط بحرانی آن هستند. اثبات شرط لازم با استفاده از «قضیه فرما» (Fermat’s Theorem) انجام می‌شود.

توجه کنید که شرایط لازم وجود اکسترمم را تضمین نمی‌کند. به عنوان مثال، تابع $$ f ( x ) = x ^ 3 $$ را در نظر بگیرید. علی‌رغم اینکه مشتق تابع در نقطه $$ x = 0 $$ صفر است ($$ f' ( x = 0 ) = 0 $$)، این نقطه یک اکسترمم نیست.

اکسترمم محلی توابع مشتق‌پذیر زمانی وجود دارد که شرایط کافی برقرار باشد. این شرایط بر اساس مشتق‌های مرتبه اول، دوم و سوم هستند. اکنون به فرمول‌بندی و اثبات این شرایط می‌پردازیم.

آزمون مشتق اول

فرض کنید تابع $$  f ( x ) $$ در همسایگی نقطه $$ x _ 0 $$ مشتق‌پذیر باشد، شاید به جز در خود $$ x _ 0 $$ که تابع پیوسته است. بنابراین:

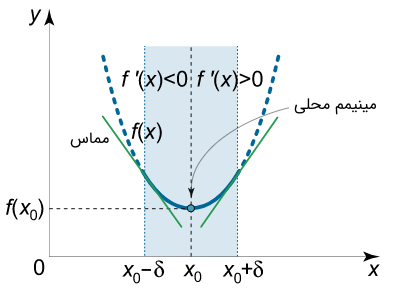
• اگر با عبور از نقطه $$ x _ 0 $$ (از چپ به راست) علامت مشتق $$ f' ( x ) $$ از منفی به مثبت تغییر کند، آنگاه $$ x _ 0 $$ یک نقطه مینیمم اکید است (شکل ۲). به عبارت دیگر، در این حالت، عدد $$ \delta > 0 $$ به گونه‌ای وجود دارد که

$$ \large { \forall \; x \in \left ( { { x _ 0 } – \delta , { x _ 0 } } \right ) } \Rightarrow { f’ \left ( x \right ) \lt 0 , } $$

$$ \large { \forall \; x \in \left ( { { x _ 0 } , { x _ 0 } + \delta } \right ) } \Rightarrow { f’ \left ( x \right ) \gt 0 . } $$

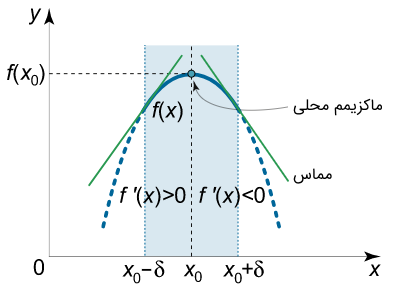
• اگر با عبور از نقطه $$ x _ 0 $$ (از چپ به راست) علامت مشتق $$ f' ( x ) $$ از مثبت به منفی تغییر کند، آنگاه $$ x _ 0 $$ یک نقطه ماکزیمم اکید است (شکل ۳). به عبارت دیگر، در این حالت، عدد $$ \delta > 0 $$ به گونه‌ای وجود دارد که

$$ \large { \forall \; x \in \left ( { { x _ 0 } – \delta , { x _ 0 } } \right ) } \Rightarrow { f’ \left ( x \right ) \gt 0 , } $$

$$ \large { \forall \; x \in \left ( { { x _ 0 } , { x _ 0 } + \delta } \right ) } \Rightarrow { f’ \left ( x \right ) \lt 0 . } $$

اثبات: برای اثبات،‌ مورد مینیمم را بررسی می‌کنیم. اثبات ماکزیمم مشابه است. فرض کنید علامت مشتق $$ f' ( x ) $$ هنگام عبور نقطه $$ x _ 0 $$ از منفی به مثبت تغییر می‌کند. در سمت چپ $$ x _ 0 $$ شرط زیر برقرار است:

$$ \large { \forall \; x \in \left ( { { x _ 0 } – \delta , { x _ 0 } } \right ) } \Rightarrow { f’ \left ( x \right ) < 0 . } $$

که در آن، نقطه $$ c $$ در بازه $$ \left( {{x_0} – \delta ,{x_0}} \right) $$ قرار دارد. در این نقطه مشتق منفی است، یعنی $$ f' ( c ) < 0 $$ است. از آنجا که $$ x - x _ 0 < 0 $$‌ را در سمت چپ نقطه $$ x _ 0 $$ داریم، آنگاه:

$$ \large \forall x \in \left( {{x_0} – \delta ,{x_0}} \right) \Rightarrow {f\left( x \right) – f\left( {{x_0}} \right) > 0} $$

به طور مشابه، در سمت راست نقطه $$ x _ 0 $$ داریم:

$$ \large \forall x \in \left ( { { x _ 0 } , { x _ 0 } + \delta } \right ) \Rightarrow { f \left ( x \right ) – f \left ( { { x _ 0 } } \right ) > 0 } . $$

بر اساس این تعریف، نتیجه می‌گیریم که $$ x _ 0 $$ یک نقطه مینیمم اکید از تابع $$ f ( x ) $$ است.

به طور مشابه، می‌توانیم آزمون مشتق اول را برای یک ماکزیمم اثبات کنیم.

توجه کنید که در آزمون مشتق اول نیازی نیست تابع در $$ x _ 0 $$ مشتق‌پذیر باشد. اگر مشتق در این نقطه بینهایت باشد یا وجود نداشته باشد (یعنی نقطه $$ x _ 0 $$ بحرانی باشد، اما مانا نباشد)، آزمون مشتق اول را هنوز می‌توان برای اکسترمم محلی تابع به کار برد.

آزمون مشتق دوم

فرض کنید مشتق اول تابع $$ f ( x ) $$ در نقطه $$ x _ 0 $$ برابر با صفر باشد ($$ f' ( x _ 0 ) = 0 $$) که یعنی $$ x _ 0 $$ یک نقطه مانا از $$ f ( x ) $$ است. همچنین فرض کنید مشتق دوم $$ f ^ {\prime \prime } ( x _ 0 ) $$ در این نقطه وجود داشته باشد. در نتیجه:

• اگر $$ f ^ {\prime \prime } ( x _ 0 ) > 0 $$ باشد، آنگاه $$ x _ 0 $$ یک نقطه مینیمم اکید تابع $$ f ( x) $$ است.
• اگر $$ f ^ {\prime \prime } ( x _ 0 ) < 0 $$ باشد، آنگاه $$ x _ 0 $$ یک نقطه ماکزیمم اکید تابع $$ f ( x) $$ است.

اثبات: در حالت یک مینیمم اکید، $$ f ^ {\prime \prime } ( x _ 0 ) > 0 $$ است. در نتیجه، مشتق اول یک تابع صعودی در نقطه $$ x _ 0 $$ است. بنابراین، عدد $$ \delta > 0 $$ به گونه‌ای وجود دارد که

$$ \large { \forall \; x \in \left ( { { x _ 0 } – \delta , { x _ 0 } } \right ) } \Rightarrow { f’ \left ( x \right ) \lt f’ \left ( { { x _ 0 } } \right ) , } $$

$$ \large { \forall \; x \in \left ( { { x _ 0 } , { x _ 0 } + \delta } \right ) } \Rightarrow { f’ \left ( x \right ) \gt f’ \left ( { { x _ 0 } } \right ) . } $$

از آنجا که $$ f ^ {\prime \prime } ( x _ 0 ) = 0 $$ (زیرا $$ x _ 0 $$ یک نقطه مانا است)، مشتق اول در همسایگی $$ \delta $$ در سمت چپ نقطه $$ x _ 0 $$ منفی و در سمت راست آن مثبت است؛ یعنی علامت مشتق هنگام عبور از نقطه $$ x _ 0 $$، از منفی به مثبت تغییر می‌کند. با استفاده از آزمون مشتق اول، این یعنی $$ x _ 0 $$ یک نقطه مینیمم اکید است.

حالت ماکزیمم را نیز می‌توان به طور مشابه بررسی کرد.

وقتی محاسبه مشتق اول در همسایگی یک نقطه مانا مشکل باشد، بهتر است از آزمون مشتق دوم استفاده کنیم. از طرف دیگر، از آزمون دوم تنها می‌توان برای نقاط مانا استفاده کرد (که در آن‌ها مشتق اول صفر است)، برخلاف آزمون مشتق اول که به هر نقطه بحرانی قابل اعمال است.

آزمون مشتق سوم

فرض کنید تابع $$ f ( x ) $$ در نقطه $$ x _ 0 $$ دارای مشتق تا مرتبه $$ n$$ باشد. بنابراین، اگر

$$ \large { f’ \left ( { { x _ 0 } } \right ) } = { f ^ { \prime \prime } \left ( { { x _ 0 } } \right ) = \ldots } = { { f ^ { \left ( { n – 1 } \right ) } } \left ( { { x _ 0 } } \right ) = 0 \; \; \; } \kern-0.3pt { \text{, } \; \; { f ^ { \left ( n \right ) } } \left ( { { x _ 0 } } \right ) \ne 0 , } $$

نقطه $$ x _ 0 $$ برای $$ n $$ زوج:

• یک نقطه مینیمم اکید است اگر $$ {f^{\left( n \right)}}\left( {{x_0}} \right) \gt 0 $$ و
• یک نقطه ماکزیمم اکید است اگر $$ {f^{\left( n \right)}}\left( {{x_0}} \right) \lt 0 $$.

برای $$ n $$ فرد، در $$ x_ 0 $$ اکسترمم وجود ندارد.

واضح است که برای $$ n = 2 $$، یک حالت خاص آزمون مشتق دوم برای اکسترمم محلی است. به همین دلیل آزمون مشتق سوم را برای $$ n > 2 $$ می‌نویسیم.

اثبات: بسط تابع $$ f ( x ) $$ در نقطه $$ x _ 0 $$ به صورت سری تیلور زیر است:‌

$$ \large \begin {align*} f \left ( x \right ) & = f \left ( { { x _ 0 } } \right )
+ { \frac { { f’ \left ( { { x _ 0 } } \right ) } } { { 1 ! } } \left ( { x – { x _ 0 } } \right ) }
+ { \frac { { f ^ { \prime \prime } \left ( { { x _ 0 } } \right ) } } { { 2 ! } } { \left ( { x – { x _ 0 } } \right ) ^ 2 } + \ldots } \\ & \; \; \; \;
+ { \frac { { { f ^ { \left ( { n – 1 } \right ) } } \left ( { { x _ 0 } } \right ) } } { { \left ( { n – 1 } \right ) ! } } { \left ( { x – { x _ 0 } } \right ) ^ { n – 1 } } }
+ { \frac { { { f ^ { \left ( n \right ) } } \left ( { { x _ 0 } } \right ) } } { { n ! } } { \left ( { x – { x _ 0 } } \right ) ^ n } }
+ { \omicron \left ( { { { \left ( { x – { x _ 0 } } \right ) } ^ n } } \right ) . } \end {align*} $$

از آنجا که طبق فرض، همه مشتق‌های اول تا $$ (n - 1 )$$اُم برابر با صفر هستند، خواهیم داشت:

$$ \large { f \left ( x \right ) – f \left ( { { x _ 0 } } \right ) } = { \frac { { { f ^ { \left ( n \right ) } } \left ( { { x _ 0 } } \right ) } } { { n ! } } { \left ( { x – { x _ 0 } } \right ) ^ n } } + { \omicron \left ( { { { \left ( { x – { x _ 0 } } \right ) } ^ n } } \right ) , } $$

که در آن، باقیمانده $$ \omicron\left( {{{\left( {x – {x_0}} \right)}^n}} \right) $$ درجه‌ای بزرگ‌تر از $$ n $$ دارد. در نتیجه، علامت تفاضل $$ f ( x ) - f ( x _ 0 ) $$ در همسایگی $$ \delta $$ نقطه $$ x _ 0 $$ با علامت جمله $$ n$$اُم در سری تیلور مشخص شده است:

$$ \large { \text {sign} \left [ { f \left ( x \right ) – f \left ( { { x _ 0 } } \right ) } \right] } = { \text {sign} \left [ { \frac { { { f ^ { \left ( n \right ) } } \left ( { { x _ 0 } } \right ) } } { { n ! } } { { \left ( { x – { x _ 0 } } \right ) } ^ n } } \right] } $$

یا

$$ \large { \text {sign} \left [ { f \left ( x \right ) – f \left ( { { x _ 0 } } \right ) } \right ] } = { \text {sign} \left [ { { f ^ { \left ( n \right ) } } \left ( { { x _ 0 } } \right ) { { \left ( { x – { x _ 0 } } \right ) } ^ n } } \right ] . } $$

اگر $$ n $$ یک عدد زوج باشد ($$ n = 2 k $$)، آنگاه:

$$ \large { \forall \; x \in \left ( { { x _ 0 } – \delta , { x _ 0 } + \delta } \right ) }\Rightarrow { { \left ( { x – { x _ 0 } } \right ) ^ { 2 k } } > 0 . } $$

در نتیجه، در این حالت داریم:

$$ \large { \text {sign} \left [ { f \left ( x \right ) – f \left ( { { x _ 0 } } \right ) } \right ] } = { \text {sign} { f ^ { \left ( n \right ) } } \left ( { { x _ 0 } } \right ) . } $$

اگر در همسایگی $$ \delta $$ نقطه $$ x _ 0 $$ نامساوی $$ {f^{\left( n \right)}}\left( {{x_0}} \right) \gt 0 $$ برقرار باشد، آنگاه خواهیم داشت:

$$ \large { f \left ( x \right ) – f \left ( { { x _ 0 } } \right ) } \gt 0 . $$

طبق تعریف، این بدین معنی است که $$ x _ 0 $$ یک نقطه مینیمم اکید از تابع $$ f ( x ) $$ است.

به طور مشابه، اگر در همسایگی $$ \delta $$ نقطه $$ x _ 0 $$ نامساوی $$ {f^{\left( n \right)}}\left( {{x_0}} \right) \lt 0 $$ برقرار باشد، آنگاه خواهیم داشت:

$$ \large {f\left( x \right) – f\left( {{x_0}} \right)} \lt 0, $$

که متناظر با یک نقطه ماکزیمم اکید است.

اگر $$ n $$ یک عدد فرد باشد ($$ n = 2 k + 1 $$)، وقتی از نقطه $$ x _ 0 $$ عبور می‌کنیم، درجه $$ {\left( {x – {x_0}} \right)^{2k + 1}} $$ تغییر خواهد کرد. در نتیجه، فرمول زیر را خواهیم داشت:

$$ \large { \text {sign} \left [ { f \left ( x \right ) – f \left ( { { x _ 0 } } \right ) } \right ] } = { \text {sign} \left [ { { f ^ { \left ( n \right ) } } \left ( { { x _ 0 } } \right ) { { \left ( { x – { x _ 0 } } \right ) } ^ { 2 k + 1 } } } \right ] } $$

که علامت تفاضل $$ f ( x ) - f ( x _ 0 ) $$ هنگام گذر از $$ x _ 0 $$ تغییر می‌کند. در این حالت، اکسترمم در نقطه $$ x _ 0 $$ وجود ندارد.

مثال‌های اکسترمم محلی

در این بخش، چند مثال را بررسی می‌کنیم.

مثال ۱

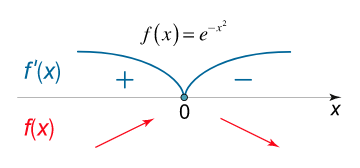
اکسترمم‌های نسبی تابع $$ f\left( x \right) = {e^{ – {x^2}}} $$ را بیابید.

حل: تابع برای همه $$ x \in \mathbb{R} $$ مشتق‌پذیر است. از آزمون مشتق اول استفاده می‌کنیم. مشتق تابع به صورت زیر است:

$$ \large { f ^ \prime \left ( x \right ) = \left ( { { e ^ { – { x ^ 2 } } } } \right ) ^ \prime } = { { e ^ { – { x ^ 2 } } } \cdot \left ( { – { x ^ 2 } } \right ) ^ \prime } = { – 2 x { e ^ { – { x ^ 2 } } } . } $$

در نتیجه، خواهیم داشت:

$$ \large { f ^ \prime \left ( x \right ) = 0 , } \; \; \Rightarrow { - 2 x { e ^ { – { x ^ 2 } } } = 0 , } \; \; \Rightarrow { x = 0 . } $$

همان‌طور که در شکل زیر نیز مشخص است، علامت مشتق تغییر می‌کند و بنابراین، تابع دارای یک ماکزیمم در $$ x = 0 $$ است. مقدار این ماکزیمم برابر است با:

$$ \large { { f _ { \max } } = f \left ( 0 \right ) } = { { e ^ { – { 0 ^ 2 } } } } = { { e ^ 0 } = 1 . } $$

مثال ۲

اکسترمم محلی (نسبی) تابع زیر را تعیین کنید.

$$ \large f \left ( x \right ) = – { x ^ 2 } + 4 x – 3 . $$

حل: این تابع در کل مجموعه اعداد حقیقی $$ \mathbb{R}$$ مشتق‌پذیر است. در نتیجه، اکسترمم‌های تابع در نقاط مانا قرار دارند. با حل معادله $$f’\left( x \right) = 0$$، داریم:

$$ \large { f’ \left ( x \right ) = { \left ( { – { x ^ 2 } + 4 x – 3} \right ) ^ \prime } } = { - 2 x + 4 , } $$

$$ \large { f’ \left ( x \right ) = 0 , \; \; } \Rightarrow { - 2 x + 4 = 0 , \; \; } \Rightarrow { x = 2 . } $$

تابع در نقطه $$ x = 2 $$ دارای نقطه مانا است. اکنون علامت مشتق را در سمت چپ و راست این نقطه تعیین می‌کنیم. مشتق برای $$ x<2 $$ مثبت و به ازای $$ x > 2 $$ منفی است. بنابراین، وقتی از نقطه $$ x = 2 $$ عبور می‌کنبم، مشتق از مثبت به منفی تغییر علامت می‌دهد. با استفاده از آزمون مشتق اول، می‌توان گفت $$ x = 2 $$ یک نقطه ماکزیمم است.

مقدار ماکزیمم تابع در نقطه مورد نظر، برابر است با:‌

$$ \large { { f _ { \max } } = f \left ( 2 \right ) } = { – { 2 ^ 2 } + 4 \cdot 2 – 3 = 1 . } $$

مثال ۳

اکسترمم‌های محلی تابع $$ f\left( x \right) = {x^3} – 12x $$ را بیابید.

حل:‌ ابتدا نقاط بحرانی را محاسبه می‌کنیم. مشتق اول به صورت زیر محاسبه می‌شود:

$$ \large { f ^ \prime \left ( x \right ) = \left ( { { x ^ 3 } – 1 2 x } \right ) ^ \prime } = { 3 { x ^ 2 } – 1 2 . } $$

مشتق در نقاط زیر برابر با صفر است:

$$ \large { f ^ \prime \left ( x \right ) = 0 , } \; \; \Rightarrow { 3 { x ^ 2 } – 1 2 = 0 , } \; \; \Rightarrow { { x ^ 2 } = 4 , } \;\; \Rightarrow { { x _ 1 } = – 2 , { x _ 2 } = 2 . } $$

این دو نقطه بحرانی هستند، زیرا تابع در $$ \mathbb { R} $$ تعریف شده و پیوسته است. مشتق نیز در $$ \mathbb { R} $$ وجود دارد، بنابراین، نقاط بحرانی دیگری وجود ندارند.

از آزمون مشتق دوم استفاده می‌کنیم:

$$ \large \begin {align*} f^{\prime\prime}\left( x \right) & = \left( {3{x^2} – 12} \right)^\prime ={ 6x,} \\ \large
f ^ { \prime \prime } \left ( { – 2 } \right ) & = 6 \cdot \left ( { – 2 } \right ) = { - 1 2 \lt 0 , } \\ f ^ { \prime \prime } \left ( { 2 } \right ) & = 6 \cdot 2 = { 1 2 \gt 0 . }
\end {align*} $$

بنابراین، $$ x = - 2 $$ یک نقطه ماکزیمم محلی است و $$ x = 2 $$ یک نقطه مینیمم محلی است.

مقادیر $$ y $$ در این نقاط به صورت زیر هستند:

$$ \large \begin {align*} { f _ { \max } } & = f \left ( { – 2 } \right ) = { { \left ( { – 2 } \right ) ^ 3 } – 1 2 \cdot \left ( { – 2 } \right ) } = { 1 6 , } \\
{ f _ { \min } } & = f \left ( 2 \right ) = { { 2 ^ 3 } – 1 2 \cdot 2 } = { – 1 6 . } \end {align*} $$

مثال ۴

نقاط اکسترمم تابع درجه سوم زیر را بیابید:

$$ \large f \left ( x \right ) = { x ^ 3 } – 3 { x ^ 2 } – 9 x + 2 . $$

حل: تابع در مجموعه اعداد حقیقی مشتق‌پذیر است. بنابراین، نقاط اکسترمم در نقاط مانا قرار دارند که در آن‌ها مشتق صفر است.

این نقاط به صورت زیر به دست می‌آیند:

$$ \large \begin {align*} & f’ \left ( x \right) = 0 , \; \; \Rightarrow { \left ( { { x ^ 3 } – 3 { x ^ 2 } – 9 x + 2 } \right )^\prime = 0 , \; \; } \\ & \Rightarrow { 3 { x ^ 2 } – 6 x – 9 = 0 , \; \; } \Rightarrow { { x ^ 2 } – 2 x – 3 = 0 , \; \; } \\ & \Rightarrow { { x _ 1 } = – 1 , \; { x _ 2 } = 3 . } \end {align*} $$

با جایگذاری نقاط آزمون $$ x $$، مشتق $$f’\left( x \right) = 3{x^2} – 6x – 9$$ را در بازه‌های مربوطه تعیین علامت می‌کنیم (شکل ۵).

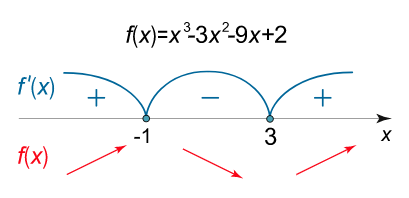
همان‌طور که می‌بینیم، وقتی از نقطه $$ x = - 1 $$ عبور می‌کنیم، علامت مشتق از مثبت به منفی تغییر می‌کند. با کمک آزمون مشتق اول، در می‌یابیم که این نقطه یک نقطه ماکزیمم محلی است. به طور مشابه، می‌توان دریافت که $$ x = 3 $$ یک نقطه مینیمم محلی است.

اکنون مقادیر ماکزیمم و مینیمم تابع را به دست می‌آوریم:

$$ \large \begin {align*} f _ { \max } & = f \left ( { – 1 } \right ) = { { \left ( { – 1 } \right ) ^ 3 } – 3 \cdot { \left ( { – 1 } \right ) ^ 2 } – 9 \cdot \left ( { – 1 } \right ) + 2 = 7 , } \\
{ f _ { \min } } & = f \left ( 3 \right ) = { { 3 ^ 3 } – 3 \cdot { 3 ^ 2 } – 9 \cdot 3 + 2 = – 2 5 . }
\end {align*} $$

مثال ۵

با استفاده از آزمون مشتق دوم، اکسترمم‌های محلی تابع زیر را محاسبه کنید:

$$ \large f \left ( x \right ) = { x ^ 3 } – 9 { x ^ 2} + 2 4 x – 7 . $$

حل: تابع برای همه $$x$$ها تعریف شده است. ابتدا مشتق اول را محاسبه کرده و نقاط بحرانی را به دست می‌آوریم:

$$ \large \begin {align*} f ^ \prime \left ( x \right ) & = { \left ( { { x ^ 3 } – 9 { x ^ 2 } + 2 4 x – 7 } \right ) ^ \prime } = { 3 { x ^ 2 } – 1 8 x + 2 4 . } \\
f ^ \prime \left ( x \right ) & = 0 , \; \; \Rightarrow { 3 { x ^ 2 } – 1 8 x + 2 4 = 0 , } \; \; \Rightarrow { 3 \left ( { { x ^ 2 } – 6 x + 8 } \right ) = 0 , } \; \; \\ & \Rightarrow { 3 \left ( { x – 2 } \right ) \left ( { x – 4 } \right ) = 0 , } \; \; \Rightarrow { { x _ 1 } = 2 , { x_ 2 } = 4 . }
\end {align*} $$

مشتق دوم نیز به صورت زیر محاسبه می‌شود:

$$ \large { f ^ { \prime \prime } \left ( x \right ) = \left ( { 3 { x ^ 2 } – 1 8 x + 2 4 } \right ) ^ \prime } = { 6 x – 1 8 . } $$

با تعیین علامت مشتق دوم در نقاط بحرانی، داریم:

$$ \large \begin {align*} f ^ { \prime \prime } \left ( { { x _ 1 } } \right ) & = { f ^ { \prime \prime } \left ( 2 \right ) } = { 6 \cdot 2 – 1 8 } = { – 6 \lt 0 . } \\
{ f ^ { \prime \prime } \left ( { { x _ 2 } } \right ) } & = { f ^ { \prime \prime } \left ( 4 \right ) } = { 6 \cdot 4 – 1 8 } = { 6 \gt 0 . }
\end {align*} $$

بنابراین، $$ x _ 1 = 2 $$ یک ماکزیمم محلی و $$ x _ 2 = 4 $$ یک مینیمم محلی است. مقادیر تابع در این نقاط به صورت زیر محاسبه می‌شود:

$$ \large \begin {align*}
{ f \left ( { { x _ 1 } } \right ) } & = { { 2 ^ 3 } – 9 \cdot { 2 ^ 2 } + 2 4 \cdot 2 – 7 } = { 1 3 , } \\
{ f \left ( { { x _ 2 } } \right ) } & = { { 4 ^ 3 } – 9 \cdot { 4 ^ 2 } + 2 4 \cdot 4 – 7 } = { 9 . }
\end {align*} $$

بنابراین، ماکزیمم محلی $$ \left( {2,13} \right) $$ و مینیمم محلی $$\left( {4,9} \right)$$ است.

مثال ۶

مینیمم تابع $$ y = {x^{\sqrt x }} $$ را محاسبه کنید.

حل: این تابع در $$ x > 0 $$ تعریف شده است. با استفاده از مشتق‌گیری لگاریتمی، از تابع مشتق می‌گیریم:

$$ \large \begin {align*} & y = { x ^ { \sqrt x } } , \; \; \Rightarrow {\ln y = \ln \left ( { { x ^ { \sqrt x } } } \right ) , } \; \; \Rightarrow { \ln y = \sqrt x \ln x , } \; \; \\ & \Rightarrow { \left ( { \ln y } \right ) ^ \prime = \left ( { \sqrt x \ln x } \right ) ^ \prime , } \Rightarrow { \frac { { y ^ \prime } } { y } = \left ( { \sqrt x } \right ) ^ \prime \cdot \ln x + \sqrt x \cdot \left ( { \ln x } \right ) ^ \prime , } \\ & \Rightarrow { \frac { { y ^ \prime } } { y } = \frac { 1 } { { 2 \sqrt x } } \cdot \ln x + \sqrt x \cdot \frac { 1 } { x } , } \; \; \Rightarrow { \frac { { y ^ \prime } } { y } = \frac { { \ln x } } { { 2 \sqrt x } } + \frac { 1 } { { \sqrt x } } , } \; \; \\ & \Rightarrow { \frac { { y ^ \prime } } { y } = \frac { { \ln x + 2 } } { { 2 \sqrt x } } , } \; \; \Rightarrow { y ^ \prime = \frac { { \ln x + 2 } } { { 2 \sqrt x } } { x ^ { \sqrt x } } . } \end {align*} $$

نقاط بحرانی را روی $$\left( {0, + \infty } \right)$$ پیدا می‌کنیم:

$$ \large { y ^ \prime = 0 , } \; \; \Rightarrow { \frac { { \ln x + 2 } } { { 2 \sqrt x } } { x ^ { \sqrt x } } = 0 , } \; \; \Rightarrow { \left \{ { \begin {array} { * { 2 0 } { l } }
{ \ln x + 2 = 0 } \\
{ x \ne 0 }
\end {array} } \right . , } \; \; \\ \large \Rightarrow { \ln x = – 2 , } \; \; \Rightarrow { x = { e ^ { – 2 } } = \frac { 1 } { {{ e ^ 2 } } } . } $$

همان‌طور که در شکل زیر نیز می‌بینیم، تابع در نقطه $$ x = {\frac{1}{{{e^2}}}} $$ دارای یک مینیمم محلی است.

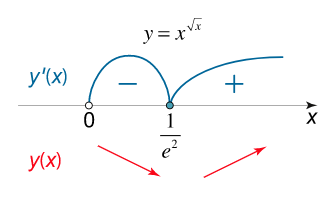
مقدار $$ y $$ در این نقطه به صورت زیر محاسبه می‌شود:

$$ \large \begin {align*} { y _ { \min } } & = y \left ( { \frac { 1 } { { { e ^ 2 } } } } \right ) = { { \left ( { \frac { 1 }{ { { e ^ 2 } } } } \right ) ^ { \sqrt { \frac { 1 } { { { e ^ 2 } } } } } } } = { { \left ( { \frac { 1 } { { { e ^ 2 } } } } \right ) ^ { \frac { 1 } { e } } } } \\ & = { { \left ( { { e ^ { – 2 } } } \right ) ^ { \frac { 1 } { e } } } = { e ^ { – \frac { 2 } { e } } } } = { \frac { 1 } { { { e ^ { \frac { 2 }{ e } } } } } \approx 0 . 4 8 } \end {align*} $$

مثال ۷

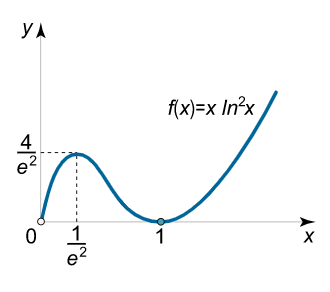
اکسترمم‌های محلی تابع $$ f\left( x \right) = x\,{\ln ^2}x $$ را بیابید.

حل: این تابع در $$ x > 0 $$ تعریف شده و مشتق‌پذیر است:

$$ \large \begin {align*} f’ \left ( x \right ) & = { \left ( { x { { \ln } ^ 2 } x } \right ) ^ \prime } = { { \left ( x \right ) ^ \prime } { \ln ^ 2 } x + x { \left ( { { { \ln } ^ 2 } x } \right ) ^ \prime } } \\ & = { { \ln ^ 2 } x + x \cdot 2 \ln x \cdot \frac { 1 } { x } } \\ & = { { \ln ^ 2 } x + 2 \ln x } = { \ln x \left ( { \ln x + 2 } \right ) ; } \end {align*} $$

$$ \large { f’ \left ( x \right ) = 0 , \; \; } \Rightarrow { \ln x \left ( { \ln x + 2 } \right ) = 0 . } $$

معادله دو جواب دارد:

$$ \large { \ln x = 0 , \; \; } \Rightarrow { { x _ 1 } = 1 ; } $$

و

$$ \large { \ln x + 2 = 0 , \; \; } \Rightarrow { { x _ 2 } = { e ^ { – 2 } } } = { \frac { 1 } { { { e ^ 2 } } } \approx 0.1 3 5 . } $$

برای تعیین نوع اکسترمم نقاط مانا، از آزمون مشتق دوم استفاده می‌کنیم. مشتق دوم تابع به صورت زیر محاسبه می‌شود:

$$ \large { f ^ { \prime \prime } \left ( x \right ) = { \left ( { { { \ln } ^ 2 } x + 2 \ln x } \right ) ^ \prime } } = { 2 \ln x \cdot \frac { 1 } { x } + \frac { 2 } { x } } = { \frac { 2 } { x } \left ( { \ln x + 1 } \right ) . } $$

در $$ x = 1 $$ و $$ x = \frac{1}{{{e^2}}} $$، مشتق دوم دارای مقادیر زیر است:

$$ \large \begin {align*} f ^ { \prime \prime } \left ( 1 \right ) & = { \frac { 2 } { 1 } \left ( { \ln 1 + 1 } \right ) = 2 \gt 0 , } \\
{ f ^ { \prime \prime } \left ( { \frac { 1 } { { { e ^ 2 } } } } \right ) } & = { \frac { 2 } { { \frac { 1 } { { { e ^ 2 }} } } } \left ( { \ln \frac { 1 } { { { e ^ 2 } } } + 1 } \right ) } = { 2 { e ^ 2 } \left ( { – 2 + 1 } \right ) } = { - 2 { e ^ 2 } \lt 0 . }
\end {align*} $$

بنابراین، تابع یک مینیمم محلی در $$ x = 1 $$ و یک ماکزیمم محلی در $$ x = {\large\frac{1}{{{e^2}}}\normalsize} $$ دارد. مقدار تابع در این نقاط برابر است با:

$$ \large \begin {align*} { f _ { \min } } & = f \left ( 1 \right ) = { 1 \cdot { \ln ^ 2 } 1 = 0 , } \\
{ f _ { \max } } & = f \left ( { \frac { 1 } { { { e ^ 2 } } } } \right ) = { \frac { 1 } {{ { e ^ 2 } } } { \ln ^ 2 } \left ( { \frac { 1 } { { { e ^ 2 } } } } \right ) } = { \frac { 4 } { { { e ^ 2 } } } \approx 0.541 . }
\end {align*} $$

این تابع در شکل ۷ نمایش داده شده است.

مثال ۸

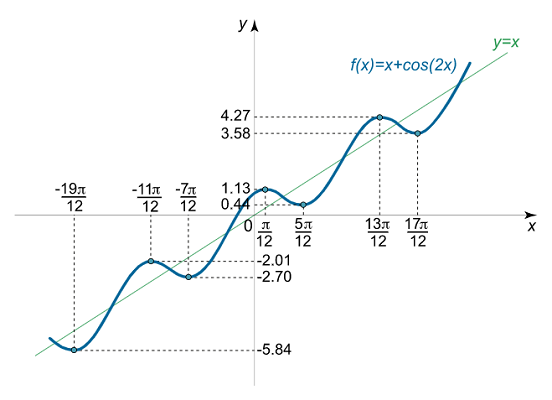
اکسترمم‌های تابع $$ f\left( x \right) = x + \cos 2x $$ را بیابید.

حل: تابع در کل مجموعه اعداد حقیقی مشتق‌پذیر است. ابتدا مشتق اول را برای به دست آوردن نقاط مانا حساب می‌کنیم:

$$ \large \begin {align*} f’ \left ( x \right ) & = { \left ( { x + \cos 2 x } \right ) ^ \prime } = { 1 – 2 \sin 2 x , } \\
f’ \left ( x \right ) & = 0 , \; \; \Rightarrow { 1 – 2 \sin 2 x = 0 , \; \; } \Rightarrow { \sin 2 x = \frac { 1 } { 2 } . }
\end {align*} $$

معادله مثلثاتی دو دسته جواب دارد:

$$ \large { 2 x = { \frac { \pi } { 6 } } + 2 \pi n , } \Rightarrow { x _ 1 } = { \frac { \pi } { { 1 2 } } } + \pi n , n \in \mathbb{Z};$$

و

$$ \large { 2 x = { \frac { 5 \pi } { 6 } } + 2 \pi k , } \Rightarrow { x _ 2 } = { \frac { 5 \pi } { { 1 2 } } } + \pi k , k \in \mathbb { Z } . $$

برای تعیین نوع اکسترمم، از آزمون مشتق دوم استفاده می‌کنیم. مشتق دوم به صورت زیر محاسبه می‌شود:

$$ \large { f ^ { \prime \prime } \left ( x \right ) = { \left ( { 1 – 2 \sin 2 x } \right ) ^ \prime } } = { – 4 \cos 2 x . } $$

برای دسته اول جواب‌های $$ \left ( { 2 x = { \frac { \pi } { 6 } } + 2 \pi n , \, n \in \mathbb { Z } } \right ) $$، مشتق دوم منفی است. بنابراین، این مجموعه متناظر با یک نقطه ماکزیمم است. دسته دوم جواب‌ها $$ ( { 2 x = { \frac { 5 \pi } { 6 } } + 2 \pi k , } { k \in \mathbb { Z } } ) $$ متناظر با مشتق دوم مثبت است. در اینجا یک نقطه مینیمم داریم. مقادیر تابع در نقاط مینیمم و ماکزیمم به صورت زیر محاسبه می‌شوند:

$$ \large \begin {align*} { f _ { \max } } & = f \left ( { \frac { \pi } { { 1 2 } } + \pi n } \right ) = { \frac { \pi } { { 1 2 } } + \pi n + \cos \left [ { 2 \left ( { \frac { \pi } { { 1 2 } } + \pi n } \right ) } \right ] } \\ & = { \frac { \pi } { { 1 2 } } + \pi n + \cos \left ( { \frac { \pi } { 6 } + 2 \pi n } \right ) } = { \frac { \pi } { { 1 2 } } + \frac { { \sqrt 3 } } { 2 } + \pi n \; } \\ & \approx { 1 , 1 3 + 3 , 1 4 n , \; \; n \in Z ; } \end {align*} $$

$$ \large \begin {align*} { f _ { \min } } & = f \left ( { \frac { 5 \pi } { { 1 2 } } + \pi k } \right ) = { \frac { 5 \pi } { { 1 2 } } + \pi k + \cos \left [ { 2 \left ( { \frac { 5 \pi } { { 1 2 } } + \pi k } \right ) } \right ] } \\ & = { \frac { 5 \pi } { { 1 2 } } + \pi k + \cos \left ( { \frac { 5 \pi } { 6 } + 2 \pi k } \right ) } = { \frac { 5 \pi } { { 1 2 } } – \frac { { \sqrt 3 } }{ 2 } + \pi k \; } \\ & \approx { 0 . 4 4 + 3 . 1 4 k, \; \; k \in Z . } \end {align*} $$

تابع این مثال، مجموع یک تابع خطی و یک تابع کسینوس است. نتیجه چنین ترکیبی این است که ماکزیمم و مینیمم به صورت خطی با افزایش تعداد $$ n $$ و $$k$$ زیاد می‌شوند. شکل زیر این مورد را به خوبی نشان می‌دهد.

مثال ۹

اکسترمم‌های محلی تابع زیر را به دست آورید.

$$ \large f \left ( x \right ) = \frac { x } { 2 } – \arctan x . $$

حل: تابع در کل مجموعه اعداد حقیقی تعریف شده و مشتق‌پذیر است. ابتدا نقاط مانا را می‌یابیم:‌

$$ \large { f’ \left ( x \right ) = { \left ( { \frac { x } { 2 } – \arctan x } \right ) ^ \prime } } = { \frac { 1 } { 2 } – \frac { 1 } { { 1 + { x ^ 2 } } } } = { \frac { { 1 + { x ^ 2 } – 2 } } { { 2 \left ( { 1 + { x ^ 2 } } \right ) } } } = { \frac { { { x ^ 2 } – 1 } } { { 2 \left ( { 1 + { x ^ 2 } } \right ) } } ; } $$

$$ \large { f’ \left ( x \right ) = 0 , \; \; } \Rightarrow
{ \frac { { { x ^ 2 } – 1 } } { { 2 \left ( { 1 + { x ^ 2 } } \right ) } } = 0 , \; \; } \Rightarrow
{ \left \{ { \begin {array} { * { 2 0 } { l } }
{ { x ^ 2 } – 1 = 0 } \\
{ 2 \left ( { 1 + { x ^ 2 } } \right ) \ne 0 }
\end {array} } \right . , \; \; } \Rightarrow
{ { x _ { 1 , 2 } } = \pm 1 . } $$

برای تعیین نوع اکسترمم این نقاط، از آزمون مشتق دوم استفاده می‌کنیم. مشتق دوم تابع به صورت زیر محاسبه می‌شود:

$$ \large \require {cancel} \begin {align*} f ^ { \prime \prime } \left ( x \right ) & = { \left ( { \frac { { { x ^ 2 } – 1 } } { { 2 + 2 { x ^ 2 } } } } \right ) ^ \prime } = { \frac { { 2 x \left ( { 2 + 2 { x ^ 2 } } \right ) – 4 x \left ( { { x ^ 2 } – 1 } \right ) } } { { { { \left ( { 2 + 2 { x ^ 2 } } \right ) } ^ 2 } } } } \\ & = { \frac { { \color {red} { 4 x } + \cancel { \color {blue} { 4 { x ^ 3 } } } – \cancel { \color {blue} { 4 { x ^ 3 } } } + \color {red} { 4 x } }} { { 4 { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } } } } = { \frac { { 2 x } } { { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } } } . } \end {align*} $$

با جایگذاری نقاط مانای $$ x = - 1 $$ و $$ x = 1 $$، داریم:

$$ \large { f ^ { \prime \prime } \left ( { – 1 } \right ) = – \frac { 1 } { 2 } \lt 0 , } \; \; \; \kern-0.3pt { f ^ { \prime \prime } \left ( 1 \right ) = \frac { 1 } { 2 } > 0 . } $$

بنابراین، $$ x = - 1 $$ یک نقطه ماکزیمم محلی و $$ x = 1 $$ مینیمم محلی است. مقادیر تابع در این نقاط به صورت زیر است:

$$ \large \begin {align*} { f _ { \max } } & = f \left ( { – 1 } \right ) = { – \frac { 1 } { 2 } – \arctan \left ( { – 1 } \right ) } = { – \frac { 1 } { 2 } + \arctan 1 } = { \frac { \pi } { 4 } – \frac { 1 } { 2 } \approx 0.29 ; } \\
{ f _ { \min } } & = f \left ( 1 \right ) = { \frac { 1 } { 2 } – \arctan 1 } = { – \left ( { \frac { \pi } { 4 } – \frac { 1 } { 2 } } \right ) \approx – 0.2 9 . }
\end {align*} $$

مثال ۱۰

نقاط اکسترمم تابع ضمنی زیر را محاسبه کنید.

$$ \large {x^2} + {y^2} – 3xy + 5 = 0. $$

حل: تحلیل را با مشتق‌گیری از تابع ضمنی آغاز می‌کنیم. با مشتق‌گیری از هر دو طرف معادله نسبت به $$ x $$، داریم:

$$ \large \begin{align*} & { \left ( { { x ^ 2 } + { y ^ 2 } – 3 x y + 5 } \right ) _ x } ^ \prime = 0 , \; \; \Rightarrow { 2 x + 2 y y’ – 3 y – 3 x y’ = 0 , \; \; } \\ &\Rightarrow { 2 x – 3 y + y’ \left ( { 2 y – 3 x } \right ) = 0 , \; } \Rightarrow { y’ = – \frac { { 2 x – 3 y } } { { 2 y – 3 x } } = \frac { { 2 x – 3 y } } { { 3 x – 2 y } } } \end {align*} $$

همان‌طور که می‌بینیم، وقتی $$3x – 2y = 0$$ باشد، یعنی $$y = {\large\frac{3x}{2}\normalsize}$$، مشتق بینهایت می‌شود. این مورد در نقاط بحرانی زیر رخ می‌دهد:

$$ \large \begin{align*} & { x ^ 2 } + { \left ( { \frac { { 3 x } }{ 2 } } \right ) ^ 2 } – 3 x \cdot \frac { { 3 x } } { 2 } + 5 = 0 , \; \; \Rightarrow { { x ^ 2 } + \frac { { 9 { x ^ 2 } } } { 4 } – \frac { { 9 { x ^ 2 } } } { 2 } + 5 = 0 , \; \; } \\ & \Rightarrow { – \frac { { 5 { x ^ 2 } } } { 4 } + 5 = 0 , \; \; } \Rightarrow { { x ^ 2 } = 4 , \; \; } \Rightarrow { x = \pm 2 . } \end {align*} $$

اکنون دامنه تابع $$ y = f ( x ) $$ را تعیین می‌کنیم. برای این کار، تابع را به فرم زیر می‌نویسیم:

$$ \large { y ^ 2 } – 3 x y + { x ^ 2 } + 5 = 0 . $$

برای به دست آوردن عبارت صریح $$ y ( x ) $$، باید معادله درجه دوم را حل کنیم. مبیّن این معادله به صورت زیر است:

$$ \large { D = { \left ( { – 3 x } \right ) ^ 2 } – 4 \left ( { { x ^ 2 } + 5 } \right ) } = { 9 { x ^ 2 } – 4 { x ^ 2 } – 2 0 } = { 5 { x ^ 2 } – 2 0 } = { 5 \left ( { { x ^ 2 } – 4 } \right ) . } $$

واضح است که تابع $$ y ( x ) $$ در صورتی وجود دارد که $${x^2} \ge 4$$ باشد. نقاط بحرانی $$ x = \pm 2$$ روی مرز دامنه $$ y ( x ) $$ هستند و طبق تعریف نمی‌توانند اکسترمم محلی باشند.

اکنون نقاط مانای درون دامنه تابع را مشخص می‌کنیم که در آن‌ها $$ y’\left( x \right) $$ صفر است:

$$ \large { y’ = \frac { { 2 x – 3 y } } { { 3 x – 2 y } } = 0 , \; \; } \Rightarrow
{ \left \{ { \begin {array} { * { 2 0 } { l } }
{ 2 x – 3 y = 0 } \\
{ 3 x – 2 y \ne 0 }
\end {array} } \right . , \; \; } \Rightarrow
{ \left \{ { \begin {array} { * { 2 0 } { l } }
{ y = \frac { 2 } { 3 } x } \\
{ y \ne \frac { 3 } { 2 } x }
\end {array}} \right . . } $$

با جایگذاری $$ y $$ در معادله اصلی، خواهیم داشت:

$$ \large \begin {align*} & { { x ^ 2 } + { \left ( { \frac { 2 } { 3 } x } \right ) ^ 2 } – 3 x \cdot \frac { 2 } { 3 } x + 5 = 0 , \; \; } \Rightarrow { { x ^ 2 } + \frac { { 4 { x ^ 2 } } } { 9 } – 2 { x ^ 2 } + 5 = 0 , \; \; }\\ & \Rightarrow { – \frac { { 5 { x ^ 2 } } } { 9 } + 5 = 0 , \; \; } \Rightarrow { { x ^ 2 } = 9 , \; \; } \Rightarrow { { x _ { 1 , 2 } } = \pm 3 . } \end {align*} $$

بنابراین، دو نقطه مانا داریم:

$$ \large { x _ 1 } = - 3 , \; \; y \left ( { – 3 } \right ) = – 2 ; \\ \large
{ x _ 2 } = 3 , \; \; y \left ( { 3 } \right ) = 2 . $$

برای تعیین نوع نقاط اکسترمم، از آزمون مشتق دوم استفاده می‌کنیم. مشتق دوم تابع به صورت زیر است:

$$ \large { y ^ { \prime \prime } = { \left ( { \frac { { 2 x – 3 y } } { { 3 x – 2 y } } } \right ) ^ \prime } } = { \frac { { { 5 y } – { 5 x y’ } } } { { { { \left ( { 3 x – 2 y } \right ) } ^ 2 } } } . } $$

با جایگذاری مختصات نقاط مانا، خواهیم داشت:

$$ \large { y ^ { \prime \prime } \left ( { – 3 , – 2 } \right ) } = { \frac { { 5 \cdot \left ( { – 2 } \right ) – 5 \cdot \left ( { – 3 } \right ) \cdot 0 } } { { { { \left ( { 3 \cdot \left ( { – 3 } \right ) – 2 \cdot \left ( { – 2 } \right ) } \right ) } ^ 2 } } } } = { – \frac { 2 } { 5 } \lt 0 , } $$

$$ \large { y ^ { \prime \prime } \left ( { 3 , 2 } \right ) } = { \frac { { 5 \cdot 2 – 5 \cdot 3 \cdot 0 } } { { { { \left ( { 3 \cdot 3 – 2 \cdot 2 } \right ) } ^ 2 } } } } = { \frac { 2 } { 5 } > 0 . } $$

بنابراین، نقطه $$\left( { – 3, – 2} \right)$$ یک ماکزیمم محلی از تابع ضمنی و نقطه $$\left( { 3, 2} \right) $$ یک مینیمم محلی است. تابع یک هذلولوی است که در شکل زیر نشان داده شده است.

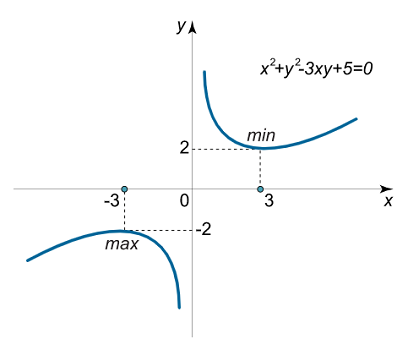
اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس ریاضیات
• آموزش جامع ریاضی دبیرستان – ریاضی و فیزیک
• مجموعه آموزش‌های دروس دبیرستان و پیش‌دانشگاهی
• آموزش ریاضیات عمومی 1
• مشتق جزئی — به زبان ساده
• ماکزیمم و مینیمم تابع — به زبان ساده
• ماکزیمم و مینیمم نسبی تابع دو متغیره — به زبان ساده

^^