سینوس و کسینوس جمع دو زاویه — به زبان ساده
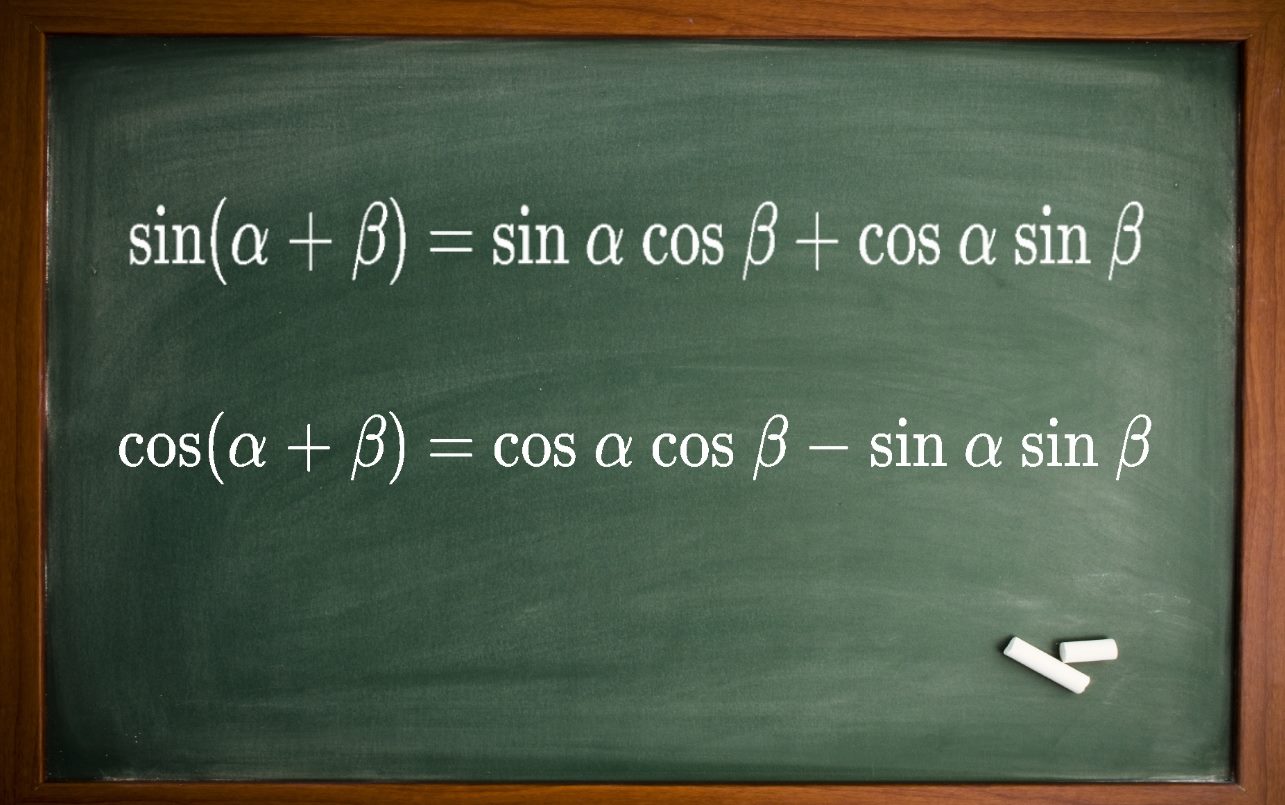
از فرمولهای پرکابرد در مثلثات، رابطه سینوس و کسینوس جمع دو زاویه است. معمولا این دو رابطه بهصورت هندسی اثبات شده و دیگر روابط مثلثاتی نیز با استفاده از این دو رابطه بدست میآیند.
سینوس و کسینوس جمع دو زاویه
در این مطلب قصد داریم تا رابطهای را اثبات کنیم که با استفاده از آن میتوان سینوس و کسینوسِ مجموع دو زاویه را بدست آورد. در ادامه رابطه مربوط به سینوس و کسینوس جمعِ دو زاویه ارائه شدهاند.
$$ \large \sin ( \alpha + \beta ) = \sin \alpha \, \cos \beta + \cos \alpha \, \sin \beta $$
$$ \large \cos ( \alpha + \beta) = \cos \alpha \, \cos \beta - \sin \alpha \, \sin \beta $$
به منظور اثبات روابط فوق، در ابتدا شکل زیر را در نظر بگیرید.
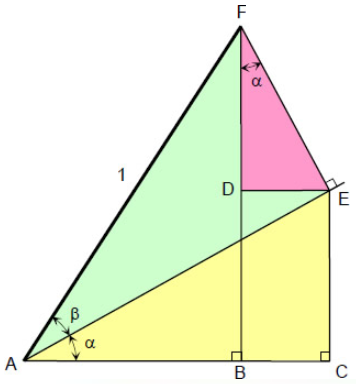
با توجه به مثلث $$ A E F $$، میتوان سینوس و کسینوسِ $$ \beta $$ را بهصورت زیر بیان کرد:
$$ \large \cos \beta = \dfrac { \overline { A E } } { 1 } ; \,\, \overline { A E } = \cos \beta $$
$$ \large \sin \beta = \dfrac { \overline { E F } } { 1 } ; \,\, \overline { E F } = \sin \beta $$
با در نظر گرفتن مثلثِ $$ E D F $$ نیز میتوان سینوس زاویه $$ \alpha $$ را مطابق با رابطه زیر بدست آورد.
$$ \large \sin \alpha = \dfrac { \overline { D E } } { \overline { E F } } $$
$$ \large \sin \alpha = \dfrac { \overline { D E } } { \sin \beta } $$
در نتیجه طول $$ D E $$ را میتوان بهصورت زیر بیان کرد:
$$ \large \overline { D E } = \sin \alpha \, \sin \beta $$
همچنین مقادیر کسینوس $$ \alpha $$ نیز برابرند با:
$$ \large \cos \alpha = \dfrac { \overline { D F } } { \overline { E F } } $$
$$ \large \cos \alpha = \dfrac { \overline { D F } } { \sin \beta } $$
در نتیجه طولهای $$ D F $$ و $$ B C $$ برابرند با:
$$ \large \overline { D F } = \cos \alpha \, \sin \beta $$
$$ \large \overline { B C } = \overline { D E } = \sin \alpha \, \sin \beta $$
با توجه به مثلثِ $$ A C E $$ نیز میتوان سینوس $$ \alpha $$ را به روشی متفاوت، همانطور که در ادامه آمده بازنویسی کرد:
$$ \large \sin \alpha = \dfrac { \overline { C E } } { \overline { A E } } $$
$$ \large \sin \alpha = \dfrac { \overline { C E } } { \cos \beta } $$
در نتیجه طولِ $$ C E $$ برابر است با:
$$ \large \overline { C E } = \sin \alpha \, \cos \beta $$
با توجه به مثلثِ $$ A C E $$، کسینوس زاویه $$\alpha$$ نیز همچون سینوس، بهصورت زیر قابل بازنویسی است.
$$ \large \cos \alpha = \dfrac { \overline { A C } } { \overline { A E } } $$
$$ \large \cos \alpha = \dfrac { \overline { A C } } { \cos \beta } $$
نهایتا طولهای $$ A C $$ و $$ B D $$ برابر با عبارات زیر بدست خواهند آمد.
$$ \large \overline { A C } = \cos \alpha \, \cos \beta $$
$$ \large \overline { B D } = \overline { C E } = \sin \alpha \, \cos \beta $$
در شکل زیر طولها بر حسب مقادیر مثلثاتی زوایا نشان داده شدهاند.
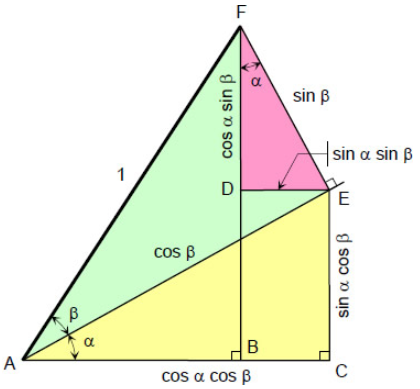
در قدم آخر، مثلثِ $$ A B F $$ را در نظر بگیرید. با توجه به این مثلث، سینوس زاویه $$ \alpha + \beta $$ برابر میشود با:
$$ \large \sin ( \alpha + \beta ) = \overline { B D } + \overline { D F } $$
حال کافی است بهجای طولهای $$ B D $$ و $$ D F $$، رابطه بدست آمده برای آنها را جایگزین کنیم. در نتیجه نهایتا سینوس مجموعِ دو زاویه، برابر با عبارت زیر بدست خواهد آمد.
$$ \boxed {\large \sin ( \alpha + \beta ) = \sin \alpha \, \cos \beta + \cos \alpha \, \sin \beta } $$
با توجه به طولهای محاسبه شده، مقدار کسینوس مجموع دو زاویه نیز برابر است با:
$$\boxed { \large \cos ( \alpha + \beta ) = \cos \alpha \, \cos \beta - \sin \alpha \, \sin \beta } $$
با بدست آمدن سینوس و کسینوس مجموع زوایا، تانژانت $$ \alpha + \beta $$ نیز بهصورت زیر بدست میآید.
$$ \large \tan ( \alpha + \beta ) = \dfrac { \sin ( \alpha + \beta ) } { \cos ( \alpha + \beta ) } $$
$$ \large \tan ( \alpha + \beta ) = \dfrac { \sin \alpha \, \cos \beta + \cos \alpha \, \sin \beta } { \cos \alpha \, \cos \beta - \sin \alpha \, \sin \beta } $$
$$ \large \tan ( \alpha + \beta ) = \dfrac { \dfrac { \sin \alpha \, \cos \beta }{ \cos \alpha \, \cos \beta } + \dfrac { \cos \alpha \, \sin \beta } { \cos \alpha \, \cos \beta } } { \dfrac { \cos \alpha \, \cos \beta } { \cos \alpha \, \cos \beta } - \dfrac { \sin \alpha \, \sin \beta } { \cos \alpha \, \cos \beta } } $$
$$ \large \tan (\alpha + \beta) = \dfrac { \dfrac { \sin \alpha } { \cos \alpha} + \dfrac { \sin \beta } { \cos \beta } } { 1 - \dfrac { \sin \alpha } { \cos \alpha} \, \dfrac { \sin \beta } { \cos \beta } } $$
در نتیجه نهایتا مقدار تانژانت مجموع دو زاویه برابر میشود با:
$$ \large \tan ( \alpha + \beta ) = \dfrac { \tan \alpha + \tan \beta } { 1 - \tan \alpha \, \tan \beta } $$
حال بهمنظور بدست آوردن رابطه مربوط به اختلاف دو زاویه، کافی است تا $$ \sin ( \alpha + \beta ) $$ را بهصورت زیر بیان کنیم:
$$ \large \sin [ \, \alpha + ( - \beta ) \, ] = \sin \alpha \, \cos ( - \beta ) + \cos \alpha \, \sin ( - \beta ) $$
توجه داشته باشید که رابطه زیر نیز برای سینوس منفیِ یک زاویه برقرار است.
$$ \large \sin ( - \beta ) = - \sin ( \beta ) $$
بنابراین با توجه به دو رابطه فوق، سینوس اختلاف دو زاویه مطابق با رابطه زیر بدست میآید.
$$ \large \sin ( \alpha - \beta ) = \sin \alpha \, \cos \beta - \cos \alpha \, \sin \beta $$
به همین ترتیب کسینوس نیز مطابق با رابطه زیر بدست میآید.
$$ \large \cos ( \alpha - \beta ) = \cos \alpha \, \cos \beta + \sin \alpha \, \sin \beta $$
نهایتا تانژانتِ اختلافِ دو زاویه نیز برابر با عبارت زیر بدست میآید.
$$ \large \tan [ \, \alpha + ( - \beta ) \, ] = \dfrac { \tan \alpha + \tan ( -\beta ) } { 1 - \tan \alpha \, \tan ( - \beta ) } $$
$$ \large \tan ( \alpha - \beta ) = \dfrac { \tan \alpha - \tan \beta } { 1 + \tan \alpha \, \tan \beta } $$
در صورت علاقهمندی به مباحث مرتبط در زمینه ریاضی، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضیات
- مجموعه آموزشهای ریاضی و فیزیک
- سینوس، کسینوس و تانژانت یک زاویه -- به زبان ساده
- بردار چیست -- به زبان ساده
- قانون سینوسها (Law of Sines) — به زبان ساده
^^











عالی ، بی نظیر . یعنی هرچقدر ازت تشکر کنیم بازم کمه . فوق العاده
عالی
درود بر شما ، بررسی ها واضح و روشن بود . بسیار ممنونم
ممنون عالی بود
توضیحات عالی بود
عالی بود ، با تشکر فراوان از شما❤
فوق العاده