نرمال سازی داده ها در SPSS | راهنمای گام به گام

در مدلهای رگرسیونی و نمایش همبستگی بین متغیر وابسته و مستقل، فرض نرمال بودن خطا یا متغیر وابسته، وجود دارد. به همین دلیل، زمانی که یک مدل رگرسیونی را برازش میکنیم، باید نرمال بودن جمله خطا یا متغیر وابسته را مورد بررسی قرار داد. ولی اگر با استفاده از آزمونهای نرمالیتی، نتوان نرمال بودن را اثبات کرد، یکی از راهحلها، نرمال سازی دادهها براساس تبدیل روی متغیر وابسته است. از آنجایی که نرمافزار SPSS، در بین کاربران محوبیت خاصی دارد، در این فرادرس به شیوه نرمال سازی داده ها در SPSS پرداخته و به کمک مثالی، گام به گام، مراحل اجرای عملیات نرمالسازی را بازگو خواهیم کرد.
برای آشنایی با نحوه ورود دادهها و پنجرههای مختلف نرمافزار SPSS، پیشنهاد میکنیم که مطالب پنجره ویرایشگر داده (Data Editor) در SPSS — راهنمای کاربردی و پنجره خروجی SPSS یا Output — راهنمای کاربردی را مطالعه کنید. همچنین خواندن نوشتارهای روشهای استاندارد سازی دادهها و نرمال سازی داده ها در خوشه بندی — به زبان ساده نیز خالی از لطف نیست.
نرمال سازی داده ها در SPSS
روشهای تجزیه و تحلیل در آمار پارامتری، وابسته به مشخص بودن توزیع جامعه آماری است. در اغلب موارد برای چنین جامعهای، «توزیع نرمال» (Normal Distribution) در نظر گرفته میشود. آزمونهایی که براساس جامعه با توزیع نرمال صورت میگیرد، نسبت به روشهای ناپارامتری مشابه، دارای «توان» (Power) بیشتری هستند. بنابراین اگر بتوانیم با دستکاری متغیرها (تبدیل- Transformation) توزیع آنها را به نرمال تغییر دهیم، نتایج حاصل از تجزیه و تحلیل آماری صورت گرفته دارای توان بیشتر و در نتیجه قدرت تعمیم بیشتری خواهد بود.
در این نوشتار از «تبدیل کاکس باکس» (Cox Box Transformation) استفاده خواهیم کرد به نحوی که در مدلهای رگرسیونی به نرمال بودن عبارت خطا یا همان متغیر پاسخ برسیم. برای به کارگیری این تبدیل نیز از نرمافزار SPSS کمک خواهیم گرفت. به یاد داشته باشید که این تبدیل، شامل چندین شیوه تغییر متغیر یا تبدیل است که با تغییر پارامتر آن، نوع تبدیل، متفاوت خواهد شد. تعیین این پارامتر نیز البته باید به شیوهای انجام شود که بهترین نتیجه حاصل گردد. در ادامه به بررسی این موضوع نیز خواهیم پرداخت.
در ادامه متن و در بخش انتهایی، بعد از پیدا کردن تبدیل مناسب باکس باکس، به کمک روشهای آزمون نرمالیتی، مانند آزمون «کولموگروف-اسمیرنف» (Kolmogorov-Smirnov)، وضعیت نرمال بودن توزیع دادهها را هم در محیط SPSS، بررسی خواهیم کرد.
تبدیل کاکس باکس برای نرمال سازی داده ها در SPSS
نرمال سازی با «تبدیل باکس کاکس» (Box-Cox Transformation)، به منظور تبدیل متغیرهای وابسته غیرنرمال به نرمال صورت میگیرد. داشتن توزیع نرمال برای متغیر وابسته یا عبارت خطا، فرض مهمی در تکنیک رگرسیون OLS محسوب میشود. اگر این دادهها، دارای توزیع نرمال نباشند، با استفاده از نرمال سازی با تبدیل باکس کاکس (Box-Cox) میتوان توزیع احتمال آنها را به نرمال نزدیک کرد. البته ممکن است همیشه این کار چاره ساز نباشد، بخصوص در مواقعی که چولگی شدید در توزیع دادهها وجود داشته باشد.
تبدیل باکس کاکس، متعلق به گروه «تبدیلهای توانی» (Power Transformation) است که توسط دو آمارشناس انگلیسی به نامهای «جورج باکس» (George Edward Pelham Box) و «دیوید کاکس» (Sir David Roxbee Cox) در سال 1964 معرفی و مورد بررسی قرار گرفت. به کمک این تبدیل میتوان توزیع دادهها را به نرمال تبدیل یا نزدیک کرد. فرم کلی برای تبدیلهای توانی مطابق با رابطه ۱ نوشته میشود.
رابطه ۱
در رابطه بالا، همان میانگین هندسی (Geometric Mean) مقادیر است. واضح است که روش محاسبه میانگین هندسی برای این مقادیر به صورت زیر است.
از آن جایی که این تبدیلها به صورت یک تابع توانی نوشته میشوند، آنها را تبدیلهای توانی میگویند.
نکته: از آنجایی که در ضابطه اول از میانگین هندسی و در ضابطه دوم از لگاریتم طبیعی مقادیر استفاده شده، باید فرض کنیم که مقادیر ، همگی مثبت هستند. البته اگر این امر محقق نشده باشد، کافی است با یک تغییر مبداء، به همه مقادیر مقدار ثابتی را اضافه کرده تا هیچ مقدار منفی برای متغیر وجود نداشته باشید.
حال فرض کنید که برای مقداری مثل ، معکوس ضربی یعنی نیز وجود داشته باشد یا اجرای عملیات ضرب روی ها، نتیجهای برابر با ۱ داشته باشند. این امر باعث میشود که میانگین هندسی برابر با یک شده () و رابطه ۱ به شکل سادهتری مانند رابطه ۲ نمایش داده شود.
رابطه ۲
رابطه ۲ را تبدیل کاکس باکس تک پارامتری میگویند. مشخص است که پارامتر این تبدیل همان است که باید با توجه به شکل تغییرات متغیر ، تعیین شود. پارامتر ، در حقیقت توان تبدیل توانی را مشخص میکند. بعضی از این تبدیلها را به ازاء مقدار در جدول ۱ مشاهده میکنید.
| نام تبدیل یا تابع | مقدار پارامتر | تبدیل |
| توان منفی سه | ||
| توان منفی دو | ||
| توان منفی یک | ||
| توان منفی نیم | ||
| توان صفر (لگاریتم) | ||
| توان نیم (ریشه دوم) | ||
| توان یک (بدون تغییر) | ||
| توان دو (مربع) | ||
| توان سه (مکعب) |
فرم دیگری نیز از تبدیل باکس کاکس که در SPSS مورد استفاده قرار میگیرد، فرم دو پارامتری است که به و وابسته است. فرمول مربوط به این تبدیل در رابطه ۳ قابل مشاهده است.
رابطه ۳
در ادامه براساس یک فایل داده، به مثالی خواهیم پرداخت که در آن نیاز است دادههای مربوط به متغیر وابسته به کمک تبدیل کاکس باکس دارای توزیع نرمال شده و در مدل رگرسیونی به کار روند. در مثال مربوط به نرمال سازی داده ها در SPSS از رابطه ۳ استفاده شده و تبدیل کاکس باکس دو پارامتری به کار گرفته میشود. مشخص است که این تبدیل، به کمک پارامتر دوم، یک جابجایی (تغییر مکان) برای مقادیر نیز به همراه دارد.
مراحل اجرای نرمال سازی داده ها در SPSS با تبدیل کاکس باکس
فرض کنید دادههای مطابق با تصویر ۱ در پنجره ویرایشگر داده نرمافزار SPSS قرار گرفته است. قرار است بین متغیر x به عنوان متغیر مستقل و متغیر y به عنوان متغیر وابسته، یک رابطه رگرسیونی ایجاد کنیم. به نظر میرسد که رابطه بین این دو متغیر، خطی نیست.
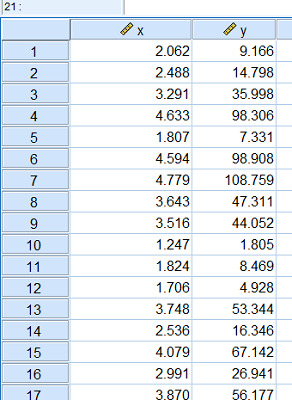
برای دسترسی به فایل اطلاعاتی مربوط به این مثال، کافی است اینجا کلیک کنید. البته فایل دریافتی با نام Normalize data.zip به صورت فشرده است. کافی است پس از خارج کردن آن از حالت فشرده، در محیط SPSS، آن را بارگذاری کنید. تصویر ۲، نمودار نقطهای و پراکندگی برای این دو متغیر را نشان میدهد. وجود یک رابطه سهمی شکل (نه خطی) بین دو متغیر به خوبی دیده میشود.
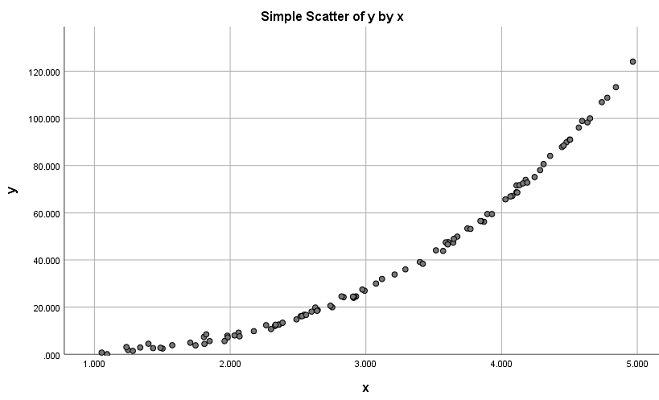
این نمودار را به کمک دستور رسم نمودار Scatter/Dot در SPSS رسم کردهایم. در اینجا لازم است به این نکته اشاره کنیم که برای آشنایی با نحوه ترسیم نمودار در SPSS، میتوانید مطلب رسم نمودار در SPSS — راهنمای کاربردی را مطالعه کنید.
کد دستوری برای انجام این کار در ادامه دیده میشود.
1DATASET ACTIVATE DataSet2.
2* Chart Builder.
3GGRAPH
4 /GRAPHDATASET NAME="graphdataset" VARIABLES=x y MISSING=LISTWISE REPORTMISSING=NO
5 /GRAPHSPEC SOURCE=INLINE
6 /FITLINE TOTAL=NO.
7BEGIN GPL
8 SOURCE: s=userSource(id("graphdataset"))
9 DATA: x=col(source(s), name("x"))
10 DATA: y=col(source(s), name("y"))
11 GUIDE: axis(dim(1), label("x"))
12 GUIDE: axis(dim(2), label("y"))
13 GUIDE: text.title(label("Simple Scatter of y by x"))
14 ELEMENT: point(position(x*y))
15END GPL.حال به نرمال سازی داده ها در SPSS به کمک تبدیل کاکس باکس میپردازیم. از آنجایی که پیدا کردن بهترین مقدار برای ها احتیاج به تکرار عملیات تبدیل دارد، از SPSS میخواهیم بهترین برآورد را برای پارامترهای و در تبدیل کاکس باکس، پیدا کند. گامهای پیش رو، مراحل انجام این عملیات را مشخص کردهاند.
- گام اول: اجرای دستور Prepare Data for Modeling از فهرست Transform.
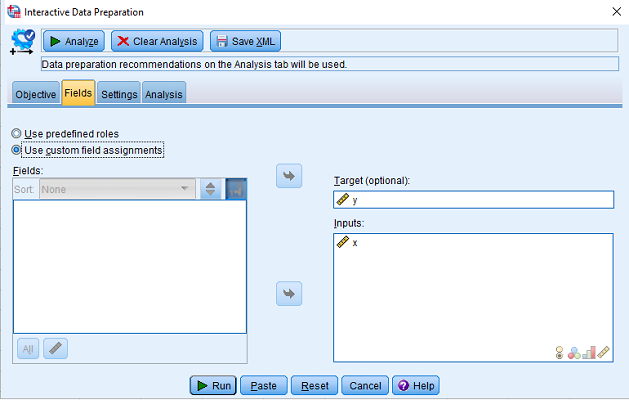
- گام دوم: انتخاب متغیرهای دخیل در مدل آماری در برگه Fields. در اینجا متغیر y در کادر Target و متغیر x در کادر Inputs قرار میگیرد. به تصویر ۳ توجه کنید. واضح است که y، نقش متغیر وابسته و x، متغیر مستقل (توصیفی- رگرسور) است.
- گام سوم: اجرای تبدیل کاکس باکس برای متغیرهای مدل در برگه Settings و بخش Rescale Fields. طبق تصویر ۴.
- گام چهارم: اجرای تبدیل با استفاده از دکمه Run و مشاهده متغیرهای جدید تولید شده در پنجره ویرایشگر داده (Data Editor).
توجه داشته باشید که تغییر متغیر روی متغیر مستقل که در بخش Inputs معرفی کردید، فقط به صورت استاندارد سازی خواهد بود و تبدیل نرمال روی آن اجرا نخواهد شد. بنابراین باید حتما یک متغیر وابسته در مدل برای ایجاد متغیر نرمال به کار برده باشید.
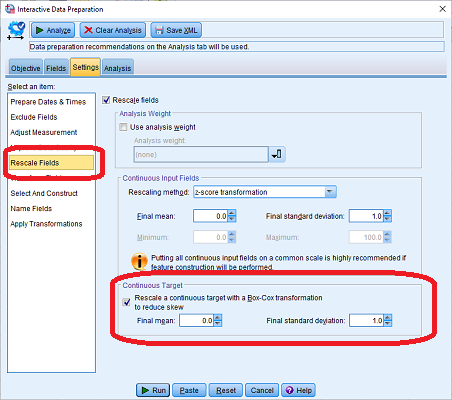
همانطور که در شکل ۴، مشاهده میکنید، پس از انتخاب گزینه ...Rescale a cont، میانگین نهایی دادهها (Final mean) در توزیع نرمال برابر با صفر و واریانس یا انحراف استاندارد (Final standard deviation) برابر با ۱ منظور شده است.
نکته: بهتر است برای افزایش سرعت در عملیات، گزینههای دیگر از کادر Select an item را انتخاب و هر یک را غیرفعال کنید.
کد دستوری برای اجرای این دستور در ادامه قابل مشاهده است.
1Interactive Data Preparation.
2COMPUTE x_transformed = (((1/1.0703390112737)*(x-3.07138825))+0).
3COMPUTE y_transformed = (((1/5.46021529521483)*(((((y-(-0.96967641))**0.5)-1)/0.5)-9.47091826523941)
4 )+0).
5VARIABLE ROLE
6 /NONE x y
7 /TARGET y_transformed
8 /INPUT x_transformed.
9EXECUTE.همانطور که در کد بالا میبینید، تبدیلهای صورت گرفته برای متغیر مستقل، محاسبه Z-score با میانگین ۳٫07138 و انحراف معیار 1٫07033 بوده و برای متغیر وابسته، تبدیل کاکس باکس با پارامترهای برآورد شده و طبق رابطه ۳، مورد استفاده قرار گرفته است.
اگر میخواهید در مورد تبدیلهای اجرا شده و متغیرهای جدیدی که تولید شدهاند، اطلاعات بیشتری دریافت کنید، قبل از اجرا و کلیک کردن روی دکمه Run، دکمه Analyze را از بالای پنجره، کلیک کرده، سپس برگه Analyze را مشاهده کنید. بسیاری از اطلاعات، نظیر توزیع دادههای اصلی و تبدیل یافته در این بخش قابل مشاهده است. قسمتهای مهم برای این پنجره در تصویر ۵ متمایز شدهاند.
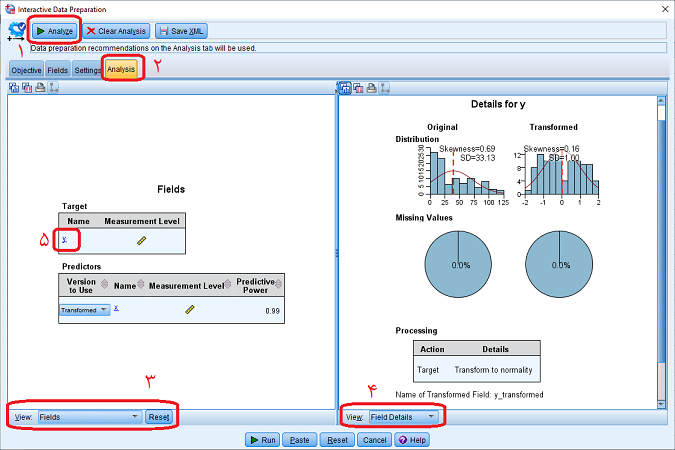
البته توجه داشته باشید که باید نوع نمایش برای هر یک از قابها در قسمت (View) از حالت اولیه تغییر دهید. برای مثال کادر سمت چپ باید در قسمت View، با گزینه Fields تنظیم شده باشد. همچنین کادر سمت راست نیز Field Details در قسمت View فعال باشد.
همانطور که در کادر سمت راست و روی نمودارهای ستونی پنجره مربوط به تصویر ۵ مشاهده میکنید، «میزان چولگی» (Skewness) متغیر اصلی (متغیر وابسته) بسیار زیاد (۰٫۶۹) است در حالیکه پس از تبدیل میزان چولگی به ۰٫۱۶ کاهش یافته است.
حال به نموداری که در تصویر ۶، براساس متغیرهای تبدیل یافته برای نمایش ارتباط بین آنها ایجاد کردهایم، توجه کنید. این نمودار نقطهای (Scatter/Dot)، به خوبی نمایانگر «رابطه خطی» (Linear Relation) مناسب بین دو متغیر است.
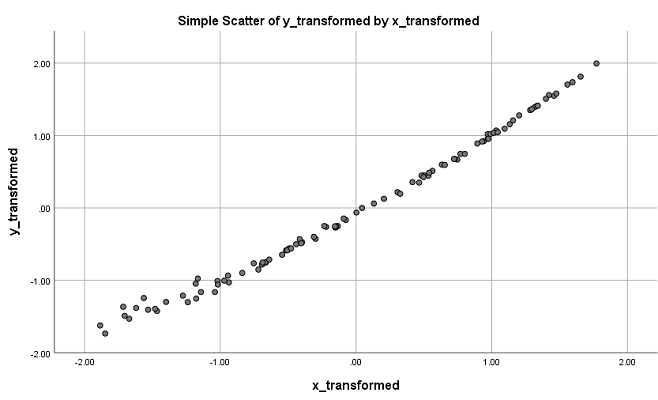
حال میتوانید یک مدل رگرسیونی بین متغیرهای تبدیل یافته به کمک نرمال سازی داده ها در SPSS اجرا کنید. به این ترتیب قادر به پیشگویی متغیر وابسته برحسب مقادیر مختلف متغیر مستقل تبدیل یافته، خواهید بود. البته اگر این مدل را برای پیشبینی به کار بردید، باید پس از محاسبه مقدار متغیر وابسته، با تبدیل عکس، متغیر وابسته واقعی را برآورد کنید.
بررسی نرمال بودن متغیر تبدیل یافته
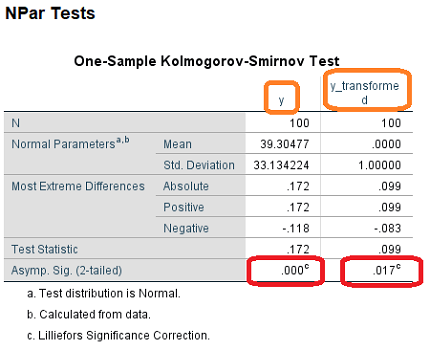
این بار میخواهیم به کمک آزمون «کولموگروف-اسمیرنف» (Kolmogorov-Smirnov)، در SPSS، به بررسی نرمال بودن دادههای مربوط به متغیرهای و $$\text{y_transformed}$$
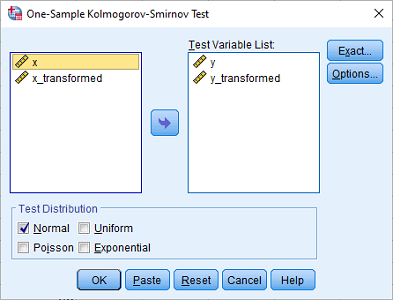
به این منظور، از فهرست Analyze گزینه Nonparametric Tests را انتخاب و از فهرست ظاهر شده، گزینه Legacy Dialogs، سپس را اجرا میکنیم. تنظیمات پنجره را مطابق با تصویر 8 انجام داده و دکمه OK را کلیک میکنیم.
خروجیها مطابق با تصویر ۹ ظاهر میشوند. همانطور که در جدول One-Sample Kolmogrov-Smirnov Test دیده میشود، در سطح خطای ۰٫۰۱، فرض نرمال بودن متغیر $$\text{y_transformed}$$
خلاصه و جمعبندی
همانطور که در این متن خواندید، نرمال سازی داده ها در SPSS به طور خودکار صورت میگیرد و پارامتر مربوط به تبدیل کاکس باکس محاسبه و به کار گرفته میشود. به این ترتیب بهترین تبدیل برای نرمال سازی متغیر وابسته در مدل رگرسیونی ساخته شده و پیشبینی براساس آن صورت میگیرد. البته توجه داشته باشید که در این حالت، برای پیشبینی مقدار واقعی باید دادههای حاصل از متغیر وابسته را با یکی تبدیل معکوس به صورت عادی درآورید تا بتوان پیشبینیها را براساس متغیرهای وابسته و مستقل اصلی، بدست آورد.
همانطور که دیدید، تبدیلهای مربوط به نرمال سازی داده ها در SPSS براساس محاسبات توانی صورت میگیرد. به همین دلیل اغلب گفته میشود که با تبدیلات لگاریتمی، جذر، توان رساندن و ... میتوان توزیع احتمالی دادههایی که نرمال نبوده یا چولگی دارند، به توزیع نرمال نزدیک کرد.













سلام. عالی بود
آیا آزمون ks به صورت پیشفرض در سطح اطمینان 5% صورت نمیگیرد؟ چطور میتوانیم به 1% ارجاع دهیم.
سوال بسیار مهم دیگر در مورد علامت c بالای نتایج آزمون ks میشه توضیح بدید؟