نرمال سازی داده ها در خوشه بندی — به زبان ساده

«خوشهبندی» (Clustering) به عنوان یکی از روشهای «یادگیری ماشین غیرنظارتی» (Unsupervised Machine Learning) در حل مسائل دستهبندی و طبقهبندی مشاهدات بسیار به کار میرود. این کار بوسیله بررسی و محاسبه «توابع فاصله» (Distance Function) براساس ویژگیهای (Attributes) مشاهدات، انجام شده و نقاط با کمترین میزان فاصله در یک گروه قرار میگیرند. مسئله مهمی که در این رابطه بوجود میآید، نرمال سازی داده ها در خوشه بندی است زیرا باید ویژگیها در محاسبه فاصله بدون مقیاس باشند تا بزرگی واحد اندازهگیری هر بُعد باعث اریبی مقدار تابع فاصله به سمت یک ویژگی نشود.
در این نوشتار به شیوههای مختلف نرمال سازی داده ها در خوشه بندی بخصوص خوشهبندی k-میانگین (K-means Clustering) اشاره خواهیم داشت. به عنوان مقدمه بهتر است مطلبهای آشنایی با خوشهبندی (Clustering) و شیوههای مختلف آن و استاندارد سازی و نرمال سازی داده ها در پایتون — راهنمای کاربردی را مطالعه کنید. همچنین خواندن نوشتار روش های ارزیابی نتایج خوشه بندی (Clustering Performance) — معیارهای درونی (Internal Index) و روش های ارزیابی نتایج خوشه بندی (Clustering Performance) — معیارهای بیرونی (External Index) نیز خالی از لطف نیست.
نرمال سازی داده ها در خوشه بندی
در فرآیند و مراحل دستهبندی، نرمال سازی داده ها در خوشه بندی (Data Normalization)، یکی از اجزای مهم به شمار میآید. شیوههای مختلفی برای نرمال سازی و استاندارد سازی وجود دارد که در مرحله «آمادهسازی دادهها» (Data Preparation) به کار میروند. در این نوشتار به بررسی سه شیوه اصلی و پر کاربرد در نرمالسازی میپردازیم که در تکنیکهای خوشهبندی به کار میروند. از آنجایی که دامنه تغییرات (Range) و مقیاس اندازهگیری هر یک از ویژگیهای مشاهدات با یکدیگر متفاوت هستند، نرمالسازی اهمیت زیادی پیدا میکند زیرا این کار باعث میشود که تابع فاصله به سمت ویژگی یا متغیر با مقیاس بزرگتر منحرف یا اریب (Basie) نشود.
در الگوریتمهای خوشهبندی تفکیکی بخصوص خوشهبندی k-میانگین از «تابع فاصله اقلیدسی» (Euclidean Distance Function) استفاده میشود. برای اندازهگیری فاصله اقلیدسی بین دو نقطه و از فرمول زیر استفاده میکنیم.
در این رابطه، نقطههای و دارای بُعد هستند و مثلا نشانگر مقدار ویژگی نقطه در بُعد ام است. در ادامه با سه شیوه نرمالسازی آشنا میشویم که اغلب در الگوریتمهای خوشهبندی با تابع فاصله اقلیدسی استفاده میشوند.
روش های نرمال سازی داده ها
همانطور که بیان شد، محاسبه فاصله باید براساس دادههای «بدون مقیاس» (Scale Free) صورت بگیرد تا ویژگی یا متغیرهای خاص با واحد اندازهگیری بزرگ، باعث اریبی در مقدار فاصله بین نقطهها نشود، در غیر این صورت ممکن است نتایج خوشهبندی بستگی زیادی به متغیری داشته باشد که دارای مقدارهای بزرگتر و در نتیجه واریانس بزرگتری است. در این نوشتار به بررسی سه روش نرمالسازی دادهها میپردازیم که در فهرست زیر معرفی شدهاند. این روشهای نرمالسازی بیشتر در هنگام استفاده از الگوریتم خوشهبندی k-میانگین به کار گرفته میشوند.
نمره استاندارد (Z-score): اگر متغیر تصادفی با توزیع نرمال با میانگین و واریانس باشد، آنگاه که به صورت زیر معرفی میشود دارای توزیع نرمال با میانگین صفر و واریانس ۱ است. در این حالت میگوییم Z دارای توزیع نرمال استاندارد است. به همین دلیل مقدارهای حاصل از محاسبه Z را «نمره استاندارد» یا گاهی «نمره Z» میگویند. در این صورت اکثر مقدارهای در فاصله ۳- تا ۳ قرار گرفته و فقط حدود 0.2% آنها در خارج از این فاصله هستند.
مقدار حداکثر-حداقل (Minimum- Maximum): فرض کنید که حداقل مقدارهای در بُعد ام را با نشان دهیم. همچنین حداکثر مقدارها را در بُعد را با نماد معرفی کنیم، در این صورت اگر این شیوه محاسبه را با علامت نشان دهیم، رابطه زیر را خواهیم داشت. مشخص است که برای دادههای نامنفی، مقدار حداکثر برابر با ۱ و حداقل صفر خواهد بود.
حال اگر مقداری بعدی باشد، محاسبه را برای هر بُعد انجام داده و بردار بعدی را براساس مقدار استاندارد شده حداکثر-حداقل مولفهها میسازیم.
رتبه (Rank): شیوه دیگر حذف مقیاس برای ویژگیهای مختلف یک مشاهده، استفاده از رتبه است. به این ترتیب مولفههای مربوط به هر ویژگی براساس رتبه آن ویژگی نسبت به مقدارهای دیگر مشخص میشوند. بنابراین اگر را تابع رتبه در نظر بگیریم، مقدار را به صوت زیر برای نرمالسازی مولفه ام به کار میبریم.
مشخص است که منظور از مقدار بُعد ام از مشاهده ام است. به این ترتیب متغیر بُعدی به یک متغیر بُعدی از رتبهها تبدیل میشود.
نکته: برای مقدارهای نرمال شده به شیوه و روش محاسباتی ، میانگین و واریانس همه مولفهها یا ویژگیها ثابت و یکسان است. یعنی در بُعد ام میانگین صفر و واریانس ۱ است. در حالیکه اگر نرمال سازی با شیوه و نحوه محاسبه صورت بگیرد، هر یک از ابعاد دارای میانگین و واریانس متفاوتی خواهند بود. متاسفانه هر دو شیوه نرمالسازی دادههای و نسبت به دادههای پرت حساس هستند و با وجود چنین مقدارهایی، تغییرات شدیدی پیدا میکنند، در حالیکه روش نرمالسازی به دلیل استفاده از رتبهها، تحت تاثیر نقاط پرت نیست.
خوشهبندی k-میانگین
یکی از روشهای معمول برای خوشهبندی دادهها، الگوریتم «k-میانگین» (k-means) است. در این الگوریتم به کمک تکرار مراحل الگوریتم، دادهها و مشاهدات به دسته یا گروههایی مجزا، تفکیک یا افراز میشوند. به همین دلیل خوشهبندی k-میانگین را در گروه «روشهای خوشهبندی تفکیکی» (Partitional Clustering Methods) قرار دادهاند. الگوریتم خوشهبندی k-میانگین در سال ۱۹65 توسط «مک کوئین» (McQueen) توسعه داده شد و تا به امروز گونههای مختلفی از آن نیز ایجاد شده است. میتوان این الگوریتم را برمبنای تابع زیان مشخص کرد. بنابراین، اگر تابع زیان را به صورت زیر مشخص کنیم، باید خوشهبندی و نقاط مرکزی (میانگین) هر خوشه به شکلی انتخاب شوند که این تابع زیان کمینه شود.
در اینجا منظور از همان فاصله اقلیدسی است که در بخش ابتدای نوشتار به آن اشاره شد. از طرفی نیز میانگین یا مرکز برای خوشه ام است. در نتیجه تعیین نقاط مرکزی برای هر خوشه، معرف خوشهها خواهد بود. به همین دلیل گاهی خوشهبندی k-میانگین را در گروه روشهای خوشهبندی Prototype قرار میدهند. الگوریتم مربوط به این روش خوشهبندی در ادامه قابل مشاهده است. در اینجا فرض میکنیم که نقاط مرکزی یا میانگینها برای اجرای الگوریتم از قبل معرفی شدهاند.
- بخش مقدار دهی: هر مشاهده یا شی را به نزدیکترین خوشه با کمترین فاصله اقلیدسی از مراکز، نسبت میدهیم. به این ترتیب آن مشاهده عضو خوشهای خواهد شد که کمترین فاصله اقلیدسی را با مرکز آن داشته باشد.
- بخش به روز رسانی: میانگین خوشههای جدید محاسبه میشود.
- تکرار مرحله ۱ و ۲ تا زمانی که تغییر زیادی در مقدار میانگین هر خوشه رخ ندهد.
واضح است که در مراحل این الگوریتم، تعداد خوشهها توسط بردار اولیه از میانگینها، تعیین شده است. یکی از ضعفهای خوشهبندی k-میانگین نیز تعیین تعداد خوشهها و وابستگی زیاد نتایج به میانگینها یا خوشههای تصادفی است که در ابتدا به الگوریتم داده میشود. بنابراین اگر نقاط اولیه را تغییر دهیم، ممکن است نتایج خوشهبندی تغییر کند.
ارزیابی نتایج خوشهبندی
برای ارزیابی نتایج خوشهبندی، معیارهای مختلفی مانند معیارهای ارزیابی درونی و بیرونی (Internal and External Criteria) وجود دارد. در این نوشتار برای اندازهگیری کارایی روش خوشهبندی از معیار ارزیابی بیرونی به نام ARI که مخفف (Adjusted Rand index) است و به معنی معیار ارزیابی رند اصلاح شده است، استفاده میکنیم. این شیوه ارزیابی، با مقایسههای دوتایی بین برچسبهای حاصل از خوشه و برچسبهای واقعی (کلاس) مشاهدات، عمل ارزیابی را انجام میدهد.
فرض کنید در اینجا تعداد عناصر مشترک در کلاس i و خوشه j باشد. همچنین نیز مجموع مقدارهای برای سطر iام و نیز جمع مقدارهای در ستون jام باشد. جدول متقاطع زیر تعداد عناصر مشترک در بین دستهها و خوشهها را نشان میدهد. منظور از Cها، خوشه و Sها نیز بیانگر کلاسها هستند. البته در اینجا فرض بر این است که ممکن است نتایج خوشهبندی k دسته و کلاسها دارای l گروه باشند.
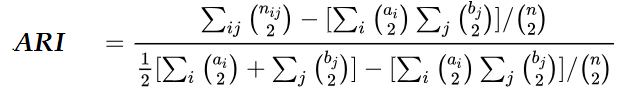

تحلیل روی دادههای واقعی
در این قسمت براساس دادههای واقعی مرسوم به iris که مربوط به خصوصیات سه نوع گل زنبق است، عمل خوشهبندی k-میانگین را انجام میدهیم. هر مشاهده از پنج ویژگی تشکیل شده است. طول و عرض کاسبرگ و گلبرگ متغیرهایی هستند که برای خوشهبندی به کار میبریم. همچنین نوع گل، خصوصیت پنجم این مجموعه محسوب میشود و دارای سه دسته مختلف است که در حقیقت کلاس یا گروههای واقعی را نشان میدهد. به منظور کسب اطلاعات بیشتر در مورد این مجموعه داده، مطلب توابع Apply در زبان برنامه نویسی R — راهنمای کاربردی را مطالعه کنید.
در کد زیر برمبنای خوشهبندی k-میانگین (kmeans) و با استفاده از متغیرهایی از ستون اول تا چهارم مجموعه داده iris که ویژگیهای گلها را نشان میدهند، عمل خوشهبندی را انجام دادهایم. نتایج برچسبگذاری خوشهبندی را با برچسبهای واقعی توسط معیار ارزیابی ARI مقایسه کردهایم. هر چه مقدار ARI بیشتر باشد، موفقیت و کارایی الگوریتم خوشهبندی بیشتر است. در اینجا با توجه به سه روش نرمالسازی دادهها (Z1, Z2 ,Z3)، عملیات خوشهبندی را انجام دادهایم و نتایج ارزیابی ARI را با هم مقایسه کردهایم.
نکته: برای محاسبه معیار ارزیابی ARI باید بسته یا کتابخانه flexclust را نصب کرده باشید. همچنین توجه داشته باشید که برای خوشهبندی k-میانگین از الگوریتم مککوئین استفاده کردهایم.
1# Flexclust library to compute Adjusted rand Index
2library(flexclust)
3# Initialization and extract data
4iter=10000
5randz1=randz2=randz3=rep(0,iter)
6mydata=iris[,1:4]
7S=as.numeric(iris[,5])
8# re-scale and data Normalization
9z1=scale(mydata) # zscore normalization
10
11maxmin=function(x) (x-min(x))/(max(x)-min(x))
12
13z2=apply(mydata,2,maxmin) # min max normalization
14
15z3=apply(mydata,2,rank,ties.method="random") # Ranking normalization
16
17#Iteration for clustering with random centers- MaxQueen k means clustering method
18
19for (i in 1:iter)
20{
21randz1[i]=randIndex(kmeans(z1,3,algorithm = "MacQueen")$cluster,S,correct = TRUE)
22randz2[i]=randIndex(kmeans(z2,3,algorithm = "MacQueen")$cluster,S,correct = TRUE)
23randz3[i]=randIndex(kmeans(z3,3,algorithm = "MacQueen")$cluster,S,correct = TRUE)
24}
25# extract mean and standatd deviation of Adjusted Rand Index
26meanrandz1=mean(randz1)
27stdrandz1=sd(randz1)
28meanrandz2=mean(randz2)
29stdrandz2=sd(randz2)
30meanrandz3=mean(randz3)
31stdrandz3=sd(randz3)
32# Comparing with Boxplot for Adjusted Rand Index
33par(mfrow=c(1,3))
34boxplot(randz1,sub="Z1 normalization method",ylim=c(0.4,0.85))
35boxplot(randz2,sub="Z2 Normalization method",ylim=c(0.4,0.85))
36boxplot(randz3,sub="Z3 Normalization method",ylim=c(0.4,0.85))
37mtext("Comparing ARI for three Nomalization Methods\n", side=3,cex = 1,adj=3)جدول زیر به مقایسه میانگین و انحراف معیار معیار ارزیابی ARI پرداخته است.
| ردیف | روش نرمال سازی | میانگین ARI | انحراف معیار ARI |
| 1 | Z-score (Z1) | 0.5842 | 0.0726 |
| 2 | Min-Max (Z2) | 0.6550 | 0.1123 |
| 3 | Rank (Z3) | 0.6462 | 0.0158 |
در انتها نیز با استفاده از سه نمودار جعبهای (Boxplot) نتایج را با هم مقایسه کردهایم. همانطور که دیده میشود در مجموعه داده iris، نرمالسازی Z2 دارای عملکرد بهتری نسبت به بقیه روشها است.
نکته: محاسبات مربوط به میانگین و انحراف معیار معیار ارزیابی خوشهبندی ARI براساس ده هزار بار تکرار الگوریتم k-میانگین بدست آمده است.

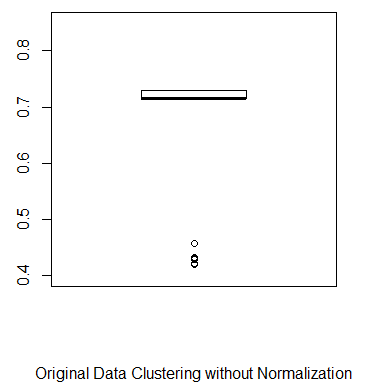
در این مرحله بد نیست به خوشهبندی روی دادههای اصلی بدون در نظر گرفتن هیچ گونه تبدیل یا نرمالسازی هم نگاهی بیاندازیم. کد زیر به این منظور نوشته شده است. باز هم به تعداد ده هزار بار مراحل خوشهبندی k-میانگین تکرار و نتیجه مربوط به معیار ارزیابی ARI مشخص شده است.
1par(mfrow=c(1,1))
2randorigin=rep(0,iter)
3for (i in 1 : iter)
4randorigin[i]=randIndex(kmeans(mydata,3,algorithm = "MacQueen")$cluster,S,correct = TRUE)
5
6meanrandorigin=mean(randorigin)
7stdrandorigin=sd(randorigin)
8boxplot(randorigin,sub="Original Data Clustering without Normalization",ylim=c(0.4,0.85))
9
10print(meanrandorigin)
11print(stdrandorigin)با کمال تعجب مشاهده میکنیم که مقدار معیار ارزیابی ARI در این حالت نسبت به حالتی که از دادههای نرمالشده استفاده کردیم، بیشتر است. جدول زیر این مطلب را نشان میدهد.
| ردیف | روش نرمال سازی | میانگین ARI | انحراف معیار ARI |
| 1 | دادههای اصلی | 0.6627 | 0.1197 |
نموداری که بوسیله کد ترسیم شده است نیز بیانگر این موضوع است که نرمالسازی برای بالا بردن کارایی روش خوشهبندی مجموعه داده iris تاثیر چندانی نداشته است.
البته علت را میتوان ناشی از آن دانست که واحد اندازهگیری همه متغیرها یکسان است و براساس واحد سنجش طول یعنی سانتیمتر است و انحراف معیار آنها تفاوت خیلی زیادی با یکدیگر ندارند. جدول زیر این میانگین و واریانس را برای این ویژگیها نشان میدهد.
| معیار | Sepal.Length | Sepal.Width | Petal.Length | Petal.Width |
| میانگین | 5.8433 | 3.0573 | 3.7580 | 1.1993 |
| انحراف معیار | 0.8281 | 0.4359 | 1.7653 | 0.7622 |
جمعبندی و نتیجهگیری
به نظر میرسد، استفاده از شیوههای نرمالسازی دادهها بسیار بستگی به نوع تابع فاصله به کار رفته در خوشهبندی و همچنین رفتار تصادفی و توزیع دادهها داشته باشد. از آنجایی که در خوشهبندی، اصل بر توصیفپذیری خروجیها است، باید روشی را برای نرمالسازی انتخاب کرد که بهترین نتیجه را با اساس تفسیرپذیر بودن دادهها داشته باشد. هر چند در مثال گفته شده، نرمالسازی موثر واقع نشد ولی در بیشتر مواقع با مواردی برخورد داریم که واحدها و مقیاسهای اندازهگیری متغیرها یا ویژگیها بسیار متفاوت هستند و تنها راهی که برای از بین بردن اثر مقیاس اندازهگیری وجود دارد، از بین بردن واحد یا هم واحد کردن متغیرها است تا نتایج خوشهبندی قابل استناد باشد.
اگر به یادگیری مباحث مشابه این مطلب علاقهمند هستید، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دادهکاوی و یادگیری ماشین
- آموزش خوشه بندی K میانگین (K-Means) با نرم افزار SPSS
- مجموعه آموزشهای آمار، احتمالات
- آموزش خوشه بندی تفکیکی با نرم افزار R
- آموزش خوشهبندی سلسله مراتبی با SPSS
- آشنایی با خوشهبندی (Clustering) و شیوههای مختلف آن
- فاصله اقلیدسی، منهتن و مینکوفسکی ــ معرفی و کاربردها در دادهکاوی
^^













تو مقالات نوروساينس روش هاي مختلفي از نرمالايز ديتا رو ديدم….
باندهاي فركانسي در مغز جونده ها به اين صورته:
دلتا(٠.١-٣هرتز)،تتا(٣-١٢هرتز)،بتا (١٢-٣٥هرتز)و گاما(٣٥-١٦٠هرتز)
حالا ما ميايم براي بررسي اكتيويتي مغز تو شرايط مختلف مثلن هنگام ترس، پاور (توان) اين باندهاي فركانسي رو حساب ميكنيم.
فيچر هاي مختلفي براي نرمالايز كردن ديدم
-معمول ترين روش z-score بود(منهاي ميانگين تقسيم بر انحراف معيار)
-relative power=
كه پاور هر باند فركانسي رو تقسيم بر مجموع كرده بود كه خب بيشترين ميشد يك و بقيه ضريبي از اون كه احتمالا خواسته اسكيل ها يكي بشه و اعداد بزرگ و كوچك كنار هم بهتر نمايش داده بشن
-يك روش هم اومده پاور مثلن دلتا رو تقسيم بر ميانگين پاور بين صفر تا ١٦٠هرتز كرده
ميخواستم ببينم هدف از نرمالايز به خصص تو روش اخر چي هستش