در آموزشهای قبلی مجله فرادس ، با مفاهیم مشتق و روشهای مشتقگیری آشنا شدیم. همچنین، مباحثی مانند مشتق لگاریتم و تابع نمایی ، مشتق ضمنی ، مشتق جزئی ، مشتق زنجیرهای ، مشتق توابع معکوس ، مشتق توابع کسری و مشتق جهتی را توضیح دادیم. در این آموزش، با مشتق رادیکال و توابع رادیکالی آشنا میشویم.
مشتق رادیکال
یک راه ساده برای محاسبه مشتق رادیکال این است که تابع رادیکالی را به صورت یک تابع توانی بنویسیم و با استفاده از قواعد مشتقگیری توابع توانی، مشتق رادیکال را محاسبه کنیم. اگر f ( x ) = x p f \left ( x \right ) = { x ^ p } f ( x ) = x p p p p عدد حقیقی است، آنگاه داریم:
( x p ) ′ = p x p – 1 . \large { \left ( { { x ^ p } } \right ) ^ \prime } = p { x ^ { p – 1 } } . ( x p ) ′ = p x p –1 .
اگر توان عددی منفی باشد، یعنی f ( x ) = x – p f \left ( x \right ) = { x ^ { – p } } f ( x ) = x – p p > 0 p>0 p > 0
( x – p ) ′ = – p x – p – 1 = – p x p + 1 . \large { \left ( { { x ^ { – p } } } \right ) ^ \prime } = { – p { x ^ { – p – 1 } } } = { – \frac { p } { { { x ^ { p + 1 } } } } . } ( x – p ) ′ = – p x – p –1 = – x p + 1 p .
اگر f ( x ) = x m f \left ( x \right ) = \sqrt [ \large m \normalsize ] { x } f ( x ) = m x 1 m \frac 1 m m 1
f ’ ( x ) = ( x m ) ′ = 1 m x m – 1 m . \large { f’ \left ( x \right ) } = { \left ( { \sqrt [ \large m \normalsize ] { x } } \right ) ^ \prime } = { \frac { 1 } { { m \sqrt [ \large m \normalsize ] { { { x ^ { m – 1 } } } } } } . } f ’ ( x ) = ( m x ) ′ = m m x m –1 1 .
به طور خاص، مشتق رادیکال فرجه دو (ریشه دوم) به شکل زیر است:
f ’ ( x ) = ( x ) ′ = 1 2 x . \large { f’ \left ( x \right ) } = { \left ( { \sqrt x } \right ) ^ \prime } = { \frac { 1 } { { 2 \sqrt x } } . } f ’ ( x ) = ( x ) ′ = 2 x 1 .
به همین ترتیب، مشتق رادیکال فرجه سه به صورت زیر به دست میآید:
f ’ ( x ) = ( x 3 ) ′ = 1 3 x 2 3 . \large { f’ \left ( x \right ) } = { \left ( { \sqrt [ \large 3 \normalsize ] { x } } \right ) ^ \prime } = { \frac { 1 }{ { 3 \sqrt [ \large 3 \normalsize ] { { { x ^ 2 } } } } } . } f ’ ( x ) = ( 3 x ) ′ = 3 3 x 2 1 .
حال اگر عبارت زیر رادیکال، خود یک تابع باشد، میتوانیم از قاعده زنجیرهای برای مشتقگیری استفاده کنیم طبق قاعده زنجیرهای اگر g ( x ) g(x) g ( x ) f ( x ) f(x) f ( x ) g ( x ) g(x) g ( x ) y = f ( g ( x ) ) y=f(g(x)) y = f ( g ( x )) u = g ( x ) u=g(x) u = g ( x )
d y d x = d y d u ⋅ d u d x \large \frac { d y } { d x } = \frac { d y } { d u } \cdot \frac { d u } { d x } d x d y = d u d y ⋅ d x d u
یا با یک نمادگذاری دیگر:
d d x [ f ( g ( x ) ) ] = f ′ ( g ( x ) ) g ′ ( x ) , d d x [ f ( u ) ] = f ′ ( u ) d u d x . \large \begin {align*} \frac { d } { d x } [ f ( g ( x ) ) ] & = f' (g(x)) g' (x ) , \\
\frac { d } { d x } [f ( u ) ] & = f' ( u ) \frac { d u } { d x } .
\end {align*} d x d [ f ( g ( x ))] d x d [ f ( u )] = f ′ ( g ( x )) g ′ ( x ) , = f ′ ( u ) d x d u .
به طور خاص، برای رادیکال فرجه ۲ تابع f ( x ) = u f ( x ) = u f ( x ) = u
f ( x ) = u \large f ( x ) = \sqrt {u} f ( x ) = u
f ′ ( x ) = u ′ 2 u \large f' (x) = \frac {u'}{2\sqrt {u}} f ′ ( x ) = 2 u u ′
مثالهای مشتق رادیکال
در این بخش، مثالهای متنوعی را از مشتق رادیکال حل میکنیم.
مثال ۱: مشتق تابع رادیکالی زیر را محاسبه کنید:
y = 7 3 x + 3 7 y = \sqrt [ \large 3 \normalsize ] { 7 } x + \sqrt [ \large 7 \normalsize ] { 3 } y = 3 7 x + 7 3
حل: مشتق رادیکال اینگونه به دست میآید:
y ’ ( x ) = ( 7 3 x + 3 7 ) ′ = ( 7 3 x ) ′ + ( 3 7 ) ′ = 7 3 ⋅ 1 + 0 = 7 3 . \large { y’ \left ( x \right ) = { \left ( { \sqrt [ \large 3 \normalsize ] { 7 } x + \sqrt [ \large 7 \normalsize ] { 3 } } \right ) ^ \prime } } = { { \left ( { \sqrt [ \large 3 \normalsize ] { 7 } x } \right ) ^ \prime } + { \left ( { \sqrt [ \large 7 \normalsize ] { 3 } } \right ) ^ \prime } } = { \sqrt [ \large 3 \normalsize ] { 7 } \cdot 1 + 0 = \sqrt [ \large 3 \normalsize ]{ 7 } . } y ’ ( x ) = ( 3 7 x + 7 3 ) ′ = ( 3 7 x ) ′ + ( 7 3 ) ′ = 3 7 ⋅ 1 + 0 = 3 7 .
مثال ۲: مشتق رادیکال زیر را به دست آورید:
y = x 3 4 . y = \large \sqrt [ 4 ] { { \small { x ^ 3 } } } . y = 4 x 3 .
حل: این مشتق رادیکال به صورت زیر به دست میآید:
y ’ ( x ) = ( x 3 4 ) ′ = ( x 3 4 ) ′ = 3 4 x 3 4 – 1 = 3 4 x – 1 4 = 3 4 x 4 . \large { y’ \left ( x \right ) = { \left ( { \sqrt [ 4 ] { { \small{ x ^ 3 } } } } \right ) ^ \prime } } = { { \left ( { { x ^ { \large \frac { 3 } { 4 } \normalsize } } } \right ) ^ \prime } } = { \frac { 3 } { 4 } { x ^ { \large \frac { 3 }{ 4 } \normalsize – 1 } } } = { \frac { 3 } { 4 } { x ^ { – \large \frac { 1 } { 4 } \normalsize } } } = { \frac { 3 } { { 4 \sqrt [ \large 4 \normalsize ] { x } } } . } y ’ ( x ) = ( 4 x 3 ) ′ = ( x 4 3 ) ′ = 4 3 x 4 3 –1 = 4 3 x – 4 1 = 4 4 x 3 .
مثال ۳: مشتق رادیکال زیر را به دست آورید.
y = 2 x 2 3 \large y = \sqrt [ 3 ] { {\small {2 x ^ 2 } } } y = 3 2 x 2
حل: مشتق رادیکال را به صورت زیر محاسبه میکنیم:
y = 2 x 2 3 = 2 3 ⋅ x 2 3 = 2 3 x 2 3 . \large { y = \sqrt [ 3 ] { \small{ 2 { x ^ 2 } } } } = { \sqrt [ 3 ] { 2 } \cdot \sqrt [ 3 ] { { \small { x ^ 2 } } } } = { \sqrt [ 3 ] { 2 }{ x ^ { \frac { 2 } { 3 } } } . } y = 3 2 x 2 = 3 2 ⋅ 3 x 2 = 3 2 x 3 2 .
y ′ = ( 2 3 x 2 3 ) ′ = 2 3 ( x 2 3 ) ′ = 2 3 ⋅ 2 3 x 2 3 – 1 = 2 3 ⋅ 2 3 x – 1 3 = 2 3 ⋅ ( 2 x ) 1 3 = 2 3 2 / x 3 . \large \begin {align*} y ^ \prime & = \left ( { \sqrt [ 3 ] { 2 } { x ^ { \frac { 2 } { 3 } } } } \right ) ^ \prime = { \sqrt [ 3 ] { 2 } \left ( { { x ^ { \frac { 2 } { 3 } } } } \right ) ^ \prime } = { \sqrt [ 3 ] { 2 } \cdot \frac { 2 } { 3 } { x ^ { \frac { 2 } { 3 } – 1 } } } \\&= { \sqrt [ 3 ] { 2 } \cdot \frac { 2 } { 3 } { x ^ { – \frac { 1 } { 3 } } } } = { \frac { 2 } { 3 } \cdot { \left ( { \frac { 2 } { x } } \right ) ^ { \frac { 1 } { 3 } } } } = { \frac { 2 } { 3 } \sqrt [ 3 ] { \small{ 2 } / { x } }} . \end {align*} y ′ = ( 3 2 x 3 2 ) ′ = 3 2 ( x 3 2 ) ′ = 3 2 ⋅ 3 2 x 3 2 –1 = 3 2 ⋅ 3 2 x – 3 1 = 3 2 ⋅ ( x 2 ) 3 1 = 3 2 3 2 / x .
مثال ۴: مشتق رادیکال x n m { \sqrt [ \large m \normalsize ] { { { x ^ n } } } } m x n
حل: این مشتق رادیکال به صورت زیر به دست میآید:
y ’ ( x ) = ( x n m ) ′ = ( x n m ) ′ = n m x n – m m = n m x – m – n m = n m x m – n m = n m x m – n m . \large \begin {align*} y’ \left ( x \right ) & = { \left ( { \sqrt [ \large m \normalsize ] { { { x ^ n } } } } \right ) ^ \prime } = { { \left ( { { x ^ { \large \frac { n } { m } \normalsize } } } \right ) ^ \prime } } = { \frac { n } { m } { x ^ { \large \frac { { n – m } } { m } \normalsize } } } \\ &= { \frac { n } { m } { x ^ { – \large \frac { { m – n } } { m } \normalsize } } } = { \frac { n } { { m { x ^ { \large \frac { { m – n } } { m } \normalsize } } } } } = { \frac { n } { { m \sqrt [ \large m \normalsize ]{ { { x ^ { m – n } } } } } } . } \end {align*} y ’ ( x ) = ( m x n ) ′ = ( x m n ) ′ = m n x m n – m = m n x – m m – n = m x m m – n n = m m x m – n n .
مثال ۵: مشتق رادیکال x 2 π { \sqrt [ \large \pi \normalsize ] { \small{ x ^ 2 } } } π x 2
حل:
y ’ ( x ) = ( x 2 π ) ′ = ( x 2 π ) ′ = 2 π x 2 π – 1 = 2 π x 2 – π π = 2 π x – π – 2 π = 2 π x π – 2 π . \large \begin {align*} y’ \left ( x \right ) & = { \left ( { \sqrt [ \large \pi \normalsize ] { \small { x ^ 2 } } } \right ) ^ \prime } = { { \left ( { { x ^ { \large \frac { 2 } { \pi } \normalsize } } } \right ) ^ \prime } } = { \frac { 2 } { \pi } { x ^ { \large \frac { 2 } { \pi } \normalsize – 1 } } }\\ & = { \frac { 2 } { \pi }{ x ^ { \large \frac { { 2 – \pi } } { \pi } \normalsize }} } = { \frac { 2 } { \pi } { x ^ { – \large \frac { { \pi – 2 } } { \pi } \normalsize } } } = { \frac { 2 } { { \pi \sqrt [ \large \pi \normalsize ] { { { x ^ { \pi – 2 } } } } } } . } \end {align*} y ’ ( x ) = ( π x 2 ) ′ = ( x π 2 ) ′ = π 2 x π 2 –1 = π 2 x π 2– π = π 2 x – π π –2 = π π x π –2 2 .
مثال ۶: مشتق تابع رادیکالی زیر را به دست آورید.
y = x 5 + 5 x y = \sqrt { \large \frac { x } { 5 } \normalsize } + \sqrt { \large \frac { 5 } { x } \normalsize } y = 5 x + x 5
حل: تابع را به صورت زیر مینویسیم:
y ( x ) = x 5 + 5 x = 1 5 ⋅ x + 5 ⋅ 1 x . \large { y \left ( x \right ) } = { \sqrt {\small \frac { x } { 5 } } + \sqrt { \small \frac { 5 } { x } } } = { \frac { 1 } { { \sqrt 5 } } \cdot \sqrt x + \sqrt 5 \cdot \frac { 1 } { { \sqrt x } } . } y ( x ) = 5 x + x 5 = 5 1 ⋅ x + 5 ⋅ x 1 .
طبق قاعده جمع، مشتق به صورت زیر نوشته میشود:
y ’ ( x ) = ( 1 5 ⋅ x + 5 ⋅ 1 x ) ′ = ( 1 5 ⋅ x ) ′ + ( 5 ⋅ 1 x ) ′ . \large { y’ \left ( x \right ) } = { { \left ( { \frac { 1 } { { \sqrt 5 } } \cdot \sqrt x + \sqrt 5 \cdot \frac { 1 } { { \sqrt x } } } \right ) ^ \prime } } = { { \left ( { \frac { 1 } { { \sqrt 5 } } \cdot \sqrt x } \right ) ^ \prime } + { \left ( { \sqrt 5 \cdot \frac { 1 } { { \sqrt x } } } \right ) ^ \prime } . } y ’ ( x ) = ( 5 1 ⋅ x + 5 ⋅ x 1 ) ′ = ( 5 1 ⋅ x ) ′ + ( 5 ⋅ x 1 ) ′ .
مشتق نیز به شکل زیر به دست میآید:
y ’ ( x ) = ( 1 5 ⋅ x ) ′ + ( 5 ⋅ 1 x ) ′ = 1 5 ( x ) ′ + 5 ( 1 x ) ′ = 1 5 ( x ) ′ + 5 ( x – 1 2 ) ′ = 1 5 ⋅ 1 2 x + 5 ⋅ ( – 1 2 ) x – 1 2 – 1 = 1 2 5 x – 5 2 x – 3 2 . \large \begin {align*} y’ \left ( x \right ) & = { { \left ( { \frac { 1 } { { \sqrt 5 } } \cdot \sqrt x } \right ) ^ \prime } + { \left ( { \sqrt 5 \cdot \frac { 1 } { { \sqrt x } } } \right ) ^ \prime } } = { \frac { 1 } { { \sqrt 5 } } { \left ( { \sqrt x } \right ) ^ \prime } + \sqrt 5 { \left ( { \frac { 1 } { { \sqrt x } } } \right ) ^ \prime } } \\ & = { \frac { 1 } { { \sqrt 5 } } { \left ( { \sqrt x } \right ) ^ \prime } + \sqrt 5 { \left ( { { x ^ { – \large \frac { 1 } { 2 } \normalsize } } } \right ) ^ \prime } } = { \frac { 1 } { { \sqrt 5 } } \cdot \frac { 1 } { { 2 \sqrt x } } + \sqrt 5 \cdot \left ( { – \frac { 1 } { 2 } } \right ) { x ^ { – \large \frac { 1 } { 2 } \normalsize – 1 } } } \\ & = { \frac { 1 }{ { 2 \sqrt 5 \sqrt x } } – \frac { { \sqrt 5 } } { 2 } { x ^ { – \large \frac { 3 } { 2 } \normalsize } } . } \end {align*} y ’ ( x ) = ( 5 1 ⋅ x ) ′ + ( 5 ⋅ x 1 ) ′ = 5 1 ( x ) ′ + 5 ( x 1 ) ′ = 5 1 ( x ) ′ + 5 ( x – 2 1 ) ′ = 5 1 ⋅ 2 x 1 + 5 ⋅ ( – 2 1 ) x – 2 1 –1 = 2 5 x 1 – 2 5 x – 2 3 .
در این مسئله، از تساوی ( x ) ′ = ( x 1 2 ) ′ = 1 2 x – 1 2 = 1 2 x { \left ( {\sqrt x } \right ) ^ \prime } = { \left ( { { x ^ { \large \frac { 1 } { 2 } \normalsize } } } \right ) ^ \prime } = { \large \frac { 1 } { 2 } \normalsize } { x ^ { – { \large \frac { 1 } { 2 } \normalsize } } } = { \large \frac { 1 } { { 2 \sqrt x } } \normalsize } ( x ) ′ = ( x 2 1 ) ′ = 2 1 x – 2 1 = 2 x 1
و با سادهسازی آن، خواهیم داشت:
y ’ ( x ) = 1 2 5 x – 5 2 x – 3 2 = 1 2 5 x – 5 2 x 3 2 = 1 ⋅ x 2 5 x ⋅ x – 5 ⋅ 5 2 x 3 2 ⋅ 5 = x – 5 2 5 x 3 2 = x – 5 2 5 x 3 . \large \begin {align*} { y’ \left ( x \right ) } & = { \frac { 1 } { { 2 \sqrt 5 \sqrt x } } – \frac { { \sqrt 5 } } { 2 } { x ^ { – \large \frac { 3 } { 2 } \normalsize } } } = { \frac { 1 } { { 2 \sqrt 5 \sqrt x } } – \frac { { \sqrt 5 } } { { 2 { x ^ { \large \frac { 3 } { 2 } \normalsize } } } } } \\ & = { \frac { { 1 \cdot x } } { { 2 \sqrt 5 \sqrt x \cdot x } } – \frac { { \sqrt 5 \cdot \sqrt 5 } } { { 2 { x ^ { \large \frac { 3 } { 2 } \normalsize } } \cdot \sqrt 5 } } } = { \frac { { x – 5 } } { { 2 \sqrt 5 { x ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { { x – 5 } } { { 2 \sqrt { 5 { x ^ 3 } } } } . } \end {align*} y ’ ( x ) = 2 5 x 1 – 2 5 x – 2 3 = 2 5 x 1 – 2 x 2 3 5 = 2 5 x ⋅ x 1 ⋅ x – 2 x 2 3 ⋅ 5 5 ⋅ 5 = 2 5 x 2 3 x –5 = 2 5 x 3 x –5 .
مثال ۷: مشتق تابع y = x 3 – 1 x 3 y = \sqrt [ \large 3 \normalsize ] { x } – { \large \frac { 1 }{ { \sqrt [ 3 ] { x } } } \normalsize } y = 3 x – 3 x 1
حل: تابع را به شکل توانی زیر مینویسیم:
y = x 3 – 1 x 3 = x 1 3 – x – 1 3 . \large { y = \sqrt [ \large 3 \normalsize ] { x } – \frac { 1 }{ { \sqrt [ \large 3 \normalsize ] { x } } } } = { { x ^ { \large \frac { 1 } { 3 } \normalsize } } – { x ^ { – \large \frac { 1 }{ 3 } \normalsize } } . } y = 3 x – 3 x 1 = x 3 1 – x – 3 1 .
اکنون از آن مشتق میگیریم:
y ’ ( x ) = ( x 1 3 – x – 1 3 ) ′ = ( x 1 3 ) ′ – ( x – 1 3 ) ′ . \large { y’ \left ( x \right ) } = { { \left ( { { x ^ { \large \frac { 1 } { 3 } \normalsize } } – { x ^ { – \large \frac { 1 }{ 3 } \normalsize } } } \right ) ^ \prime } } = { { \left ( { { x^ { \large \frac { 1 } { 3 } \normalsize } } } \right ) ^ \prime } – { \left ( { { x ^ { – \large \frac { 1 } { 3 } \normalsize } } } \right ) ^ \prime } . } y ’ ( x ) = ( x 3 1 – x – 3 1 ) ′ = ( x 3 1 ) ′ – ( x – 3 1 ) ′ .
و جواب به صورت زیر محاسبه میشود:
y ’ ( x ) = 1 3 x 1 3 – 1 – ( – 1 3 ) x – 1 3 – 1 = 1 3 x – 2 3 + 1 3 x – 4 3 = 1 3 ( x – 2 3 + x – 4 3 ) = 1 3 ( 1 x 2 3 + 1 x 4 3 ) = 1 3 ( 1 x 2 3 + 1 x 4 3 ) . \large \begin {align*} y’ \left ( x \right ) & = { \frac { 1 } { 3 }{ x ^ { \large \frac { 1 } { 3 } \normalsize – 1 } } – \left ( { – \frac { 1 } { 3 } } \right ) { x ^ { – \large \frac { 1 }{ 3 } \normalsize – 1 } } } = { \frac { 1} { 3 } { x ^ { – \large \frac { 2 } { 3 } \normalsize } } + \frac { 1 } { 3 } { x ^ { – \large \frac { 4 } { 3 } \normalsize } } } \\ & = { \frac { 1 } { 3 } \left ( { { x ^ { – \large \frac { 2 } { 3 } \normalsize } } + { x ^ { – \large \frac { 4 } { 3 } \normalsize } } } \right ) } = { \frac { 1 } { 3 } \left ( { \frac { 1 } { { { x ^ { \large \frac { 2 } { 3 } \normalsize } } } } + \frac { 1 } { { { x ^ { \large \frac { 4 } { 3 } \normalsize } } } } } \right ) } \\ &= { \frac { 1 }{ 3 } \left ( { \frac { 1 } { { \sqrt [ \large 3 \normalsize ]{ { { x ^ 2 } } } } } + \frac { 1 } { { \sqrt [ \large 3 \normalsize ]{ { { x ^ 4 } } } } } } \right ) . } \end {align*} y ’ ( x ) = 3 1 x 3 1 –1 – ( – 3 1 ) x – 3 1 –1 = 3 1 x – 3 2 + 3 1 x – 3 4 = 3 1 ( x – 3 2 + x – 3 4 ) = 3 1 x 3 2 1 + x 3 4 1 = 3 1 3 x 2 1 + 3 x 4 1 .
مثال ۸: مشتق تابع زیر را به دست آورید.
y = 1 x 4 – 1 x 5 y = \large { \frac { 1 } { { \sqrt [ 4 ] { x } } } } \normalsize – \large { \frac { 1 } { { \sqrt [ 5 ] { x } } } } \normalsize y = 4 x 1 – 5 x 1
حل: ابتدا توابع رادیکالی را به صورت تابع توانی مینویسیم:
1 x 4 = 1 x 1 4 = x – 1 4 ; 1 x 5 = 1 x 1 5 = x – 1 5 . \large \begin {align*} \frac { 1 } { { \sqrt [ 4 ] { x } } } & = \frac { 1 } { { { x ^ { \frac { 1 } { 4 } } } } } = { x ^ { – \frac { 1 } { 4 } } } ; \\
\frac { 1 } { { \sqrt [5] { x } } } & = \frac { 1 } { { { x ^ { \frac { 1 } { 5 } }} } } = { x ^ { – \frac { 1 } { 5 } } } . \end {align*} 4 x 1 5 x 1 = x 4 1 1 = x – 4 1 ; = x 5 1 1 = x – 5 1 .
در نهایت، مشتق به صورت زیر محاسبه میشود:
y ′ = ( x – 1 4 – x – 1 5 ) ′ = ( x – 1 4 ) ′ – ( x – 1 5 ) ′ = – 1 4 x – 1 4 – 1 – ( – 1 5 ) x – 1 5 – 1 = – 1 4 x – 5 4 + 1 5 x – 6 5 = 1 5 x 6 5 – 1 4 x 5 4 = 1 5 x 6 5 – 1 4 x 5 4 . \large \begin {align*}
y ^ \prime & = \left ( { { x ^ { – \frac { 1 } { 4 } } } – { x ^ { – \frac { 1 } { 5 } } } } \right ) ^ \prime = { \left ( { { x ^ { – \frac { 1 } { 4 } } } } \right ) ^ \prime – \left ( { { x ^ { – \frac { 1 } { 5 } } } } \right ) ^ \prime } = { – \frac { 1 } { 4 } { x ^ { – \frac { 1 } { 4 } – 1 } } – \left ( { – \frac { 1 }{ 5 } } \right ) { x ^ { – \frac { 1 } { 5 } – 1 } } } \\ & = { – \frac { 1 } { 4 } { x ^ { – \frac { 5 } { 4 } } } + \frac { 1 } { 5 } { x ^ { – \frac { 6 } { 5 } } } } = { \frac { 1 }{ { 5 { x ^ { \frac { 6 } { 5 } } } } } – \frac { 1 } { { 4 { x ^ { \frac { 5 } { 4 } } } } } } = { \frac { 1 } { { 5 \sqrt [ 5 ] { { { x ^ 6 } } } } } – \frac { 1 } { { 4 \sqrt [ 4 ]{ { { x ^ 5 } } } } } . } \end {align*} y ′ = ( x – 4 1 – x – 5 1 ) ′ = ( x – 4 1 ) ′ – ( x – 5 1 ) ′ = – 4 1 x – 4 1 –1 – ( – 5 1 ) x – 5 1 –1 = – 4 1 x – 4 5 + 5 1 x – 5 6 = 5 x 5 6 1 – 4 x 4 5 1 = 5 5 x 6 1 – 4 4 x 5 1 .
مثال ۹: مشتق تابع y = 5 x 3 + 3 – 2 x 3 + x 5 3 y = 5 { x ^ 3 } + 3 – { \frac { 2 } { { { x ^ 3 } } } } + \sqrt [ 3 ] { { \small { x ^ 5 } } } y = 5 x 3 + 3– x 3 2 + 3 x 5
حل: ابتدا تابع را به فرم توانی مینویسیم:
y = 5 x 3 + 3 – 2 x – 3 + x 5 3 . \large y = 5 { x ^ 3 } + 3 – 2 { x ^ { – 3 } } + { x ^ { \large \frac { 5 } { 3 } \normalsize } } . y = 5 x 3 + 3–2 x –3 + x 3 5 .
و مشتق آن به شکل زیر محاسبه میشود:
y ’ ( x ) = ( 5 x 3 + 3 – 2 x – 3 + x 5 3 ) ′ = ( 5 x 3 ) ′ + 3 ′– ( 2 x – 3 ) ′ + ( x 5 3 ) ′ = 5 ⋅ 3 x 2 + 0 – 2 ⋅ ( – 3 ) x – 3 – 1 + 5 3 x 5 3 – 1 = 15 x 2 + 6 x – 4 + 5 3 x 2 3 = 15 x 2 + 6 x 4 + 5 x 2 3 3 . \large \begin {align*} { y’ \left ( x \right ) } & = { { \left ( { 5 { x ^ 3 } + 3 – 2 { x ^ { – 3 } } + { x ^ { \large \frac { 5 }{ 3 } \normalsize } } } \right ) ^ \prime } } = { { \left ( { 5 { x ^ 3 } } \right ) ^ \prime } + 3′ – { \left ( { 2 { x ^ { – 3 } } } \right ) ^ \prime } + { \left ( { { x ^ { \large \frac { 5 }{ 3 } \normalsize } } } \right ) ^ \prime } } \\ & = { 5 \cdot 3 { x ^ 2 } + 0 – 2 \cdot \left ( { – 3 } \right ) { x ^ { – 3 – 1 } } + \frac { 5 } { 3 } { x ^ { \large \frac { 5 } { 3 } \normalsize – 1 } } } = { 1 5 { x ^ 2 } + 6 { x ^ { – 4 } } + \frac { 5 } { 3 }{ x ^ { \large \frac { 2 } { 3 } \normalsize } } } \\ & = { 1 5 { x ^ 2 } + \frac { 6 } { { { x ^ 4 } } } + \frac { { 5 \sqrt [ \large 3 \normalsize ] { { { x ^ 2 } } } } } { 3 } . } \end {align*} y ’ ( x ) = ( 5 x 3 + 3–2 x –3 + x 3 5 ) ′ = ( 5 x 3 ) ′ + 3′– ( 2 x –3 ) ′ + ( x 3 5 ) ′ = 5 ⋅ 3 x 2 + 0–2 ⋅ ( –3 ) x –3–1 + 3 5 x 3 5 –1 = 15 x 2 + 6 x –4 + 3 5 x 3 2 = 15 x 2 + x 4 6 + 3 5 3 x 2 .
مثال ۱۰: مشتق تابع y = 1 x + 1 x + 1 x 3 y = { \large \frac { 1 } { x } \normalsize } + { \large \frac { 1 } { { \sqrt x } } \normalsize } + { \large \frac { 1 } { { \sqrt [ 3 ] { x } } } \normalsize } y = x 1 + x 1 + 3 x 1
حل: این مشتق رادیکال به صورت زیر محاسبه میشود:
y ’ ( x ) = ( 1 x + 1 x + 1 x 3 ) ′ = ( 1 x ) ′ + ( 1 x ) ′ + ( 1 x 3 ) ′ = − 1 x 2 – 1 2 x – 1 2 – 1 – 1 3 x – 1 3 – 1 = – 1 x 2 – 1 2 x – 3 2 – 1 3 x – 4 3 = – 1 x 2 – 1 2 x 3 – 1 3 x 4 3 . \large \begin {align*} { y’ \left ( x \right ) } & = { { \left ( { \frac { 1 } { x } + \frac { 1 } { { \sqrt x } } + \frac { 1 }{ { \sqrt [ \large 3 \normalsize ] { x } } } } \right ) ^ \prime } } = { { \left ( { \frac { 1 } { x } } \right ) ^ \prime } + { \left ( { \frac { 1 } { { \sqrt x } } } \right ) ^ \prime } + { \left ( { \frac { 1 } { { \sqrt [ \large 3 \normalsize ] { x } } } } \right ) ^ \prime } } \\ & = { - \frac { 1 } { { { x ^ 2 } } } – \frac { 1 } { 2 } { x ^ { – \large \frac { 1 } { 2 } \normalsize – 1 } } – \frac { 1 } { 3 } { x ^ { – \large \frac { 1 } { 3 } \normalsize – 1 } } } = { – \frac { 1 } { { { x ^ 2 } } } – \frac { 1 } { 2 } { x ^ { – \large \frac { 3 } { 2 } \normalsize } } – \frac { 1 } { 3 } { x ^ { – \large \frac { 4 }{ 3 } \normalsize } } } \\ & = { – \frac { 1 } { { { x ^ 2 } } } – \frac { 1 } { { 2 \sqrt { { x ^ 3 } } } } – \frac { 1 } { { 3 \sqrt [ \large 3 \normalsize ] { { { x ^ 4 } } } } } . } \end {align*} y ’ ( x ) = ( x 1 + x 1 + 3 x 1 ) ′ = ( x 1 ) ′ + ( x 1 ) ′ + ( 3 x 1 ) ′ = − x 2 1 – 2 1 x – 2 1 –1 – 3 1 x – 3 1 –1 = – x 2 1 – 2 1 x – 2 3 – 3 1 x – 3 4 = – x 2 1 – 2 x 3 1 – 3 3 x 4 1 .
مثال ۱۱: مشتق تابع y = 2 x + 3 x 3 y = { \large \frac { 2 } { { \sqrt x } } \normalsize } + 3 \sqrt [ \large 3 \normalsize ] { x } y = x 2 + 3 3 x
حل: این مشتق رادیکال به صورت زیر به دست میآید:
y ’ ( x ) = ( 2 x + 3 x 3 ) ′ = ( 2 x – 1 2 + 3 x 1 3 ) ′ = ( 2 x – 1 2 ) ′ + ( 3 x 1 3 ) ′ = 2 ( x – 1 2 ) ′ + 3 ( x 1 3 ) ′ = 2 ⋅ ( – 1 2 ) x – 1 2 – 1 + 3 ⋅ 1 3 x 1 3 – 1 = – x – 3 2 + x – 2 3 = 1 x 2 3 – 1 x 3 . \large \begin {align*} { y’ \left ( x \right ) } & = { { \left ( { \frac { 2 } { { \sqrt x } } + 3 \sqrt [ \large 3 \normalsize ] { x } } \right ) ^ \prime } } = { { \left ( { 2 { x ^ { – \large \frac { 1 } { 2 } \normalsize } } + 3 { x ^ { \large \frac { 1 } { 3 } \normalsize } } } \right ) ^ \prime } } = { { \left ( { 2 { x ^ { – \large \frac { 1 } { 2 } \normalsize } } } \right ) ^ \prime } + { \left ( { 3 { x ^ { \large \frac { 1 } { 3 } \normalsize } } } \right ) ^ \prime } } \\ & = { 2 { \left ( { { x ^ { – \large \frac { 1 } { 2 } \normalsize } } } \right ) ^ \prime } + 3 { \left ( { { x ^ { \large \frac { 1 } { 3 } \normalsize } } } \right ) ^ \prime } } = { 2 \cdot \left ( { – \frac { 1 } { 2 } } \right ) { x ^ { – \large \frac { 1 } { 2 } \normalsize – 1 } } + 3 \cdot \frac { 1 } { 3 } { x ^ { \large \frac { 1 } { 3 } \normalsize – 1 } } } \\ & = { – { x ^ { – \large \frac { 3 } { 2 } \normalsize } } + { x ^ { – \large \frac { 2 } { 3 } \normalsize } } } = { \frac { 1 } { { \sqrt [ \large 3 \normalsize ] { { { x ^ 2 } } } } } – \frac { 1 } { { \sqrt { { x ^ 3 } } } } . } \end {align*} y ’ ( x ) = ( x 2 + 3 3 x ) ′ = ( 2 x – 2 1 + 3 x 3 1 ) ′ = ( 2 x – 2 1 ) ′ + ( 3 x 3 1 ) ′ = 2 ( x – 2 1 ) ′ + 3 ( x 3 1 ) ′ = 2 ⋅ ( – 2 1 ) x – 2 1 –1 + 3 ⋅ 3 1 x 3 1 –1 = – x – 2 3 + x – 3 2 = 3 x 2 1 – x 3 1 .
مثال ۱۲: مشتق تابع y = x – x 3 y = \sqrt x – \sqrt [ 3] { x } y = x – 3 x
حل: ابتدا تابع را به صورت توانی مینویسیم:
x = x 1 2 , x 3 = x 1 3 . \large { \sqrt x = { x ^ { \frac { 1 }{ 2 } } } , \; \; } \kern0pt { \sqrt [ 3 ] { x } = { x ^ { \frac { 1 } { 3 } } } . } x = x 2 1 , 3 x = x 3 1 .
و در ادامه، مشتق رادیکال را محاسبه میکنیم:
y ′ = ( x 1 2 – x 1 3 ) ′ = ( x 1 2 ) ′ – ( x 1 3 ) ′ = 1 2 x 1 2 – 1 – 1 3 x 1 3 – 1 = 1 2 x – 1 2 – 1 3 x – 2 3 = 1 2 x 1 2 – 1 3 x 2 3 = 1 2 x – 1 3 x 2 3 . \large \begin {align*} y ^ \prime & = \left ( { { x ^ { \frac { 1 } { 2 } } } – { x ^ { \frac { 1 } { 3 } } } } \right ) ^ \prime = { \left ( { { x ^ { \frac { 1 } { 2 } } } } \right ) ^ \prime – \left ( { { x ^ { \frac { 1 } { 3 } } } } \right ) ^ \prime } = { \frac { 1 } { 2 } { x ^ { \frac { 1 } { 2 } – 1 } } – \frac { 1 } { 3 } { x ^ { \frac { 1 } {3 } – 1 } } } \\ &= { \frac { 1 } { 2 } { x ^ { – \frac { 1 } { 2 } } } – \frac { 1 } { 3 } { x ^ { – \frac { 2 } { 3 } } } } = { \frac { 1 } { { 2 { x ^ { \frac { 1 } { 2 } } } } } – \frac { 1 } { { 3 { x ^ { \frac { 2 }{ 3 } } } } } } = { \frac { 1 } { { 2 \sqrt x } } – \frac { 1 } { { 3 \sqrt [ 3 ] { { { x ^ 2 } } } } } . } \end {align*} y ′ = ( x 2 1 – x 3 1 ) ′ = ( x 2 1 ) ′ – ( x 3 1 ) ′ = 2 1 x 2 1 –1 – 3 1 x 3 1 –1 = 2 1 x – 2 1 – 3 1 x – 3 2 = 2 x 2 1 1 – 3 x 3 2 1 = 2 x 1 – 3 3 x 2 1 .
مثال ۱۳: حاصل مشتق رادیکال y = x x y = \sqrt { x \sqrt x } y = x x
حل:
y ’ ( x ) = ( x x ) ′ = ( x ⋅ x 1 2 ) ′ = ( x 3 2 ) ′ = ( ( x 3 2 ) 1 2 ) ′ = ( x 3 4 ) ′ = 3 4 x 3 4 – 1 = 3 4 x – 1 4 = 3 4 x 4 . \large \begin {align*}
y’ \left ( x \right ) & = { \left ( { \sqrt { x \sqrt x } } \right ) ^ \prime } = { { \left ( { \sqrt { x \cdot { x ^ { \large \frac { 1 }{ 2 } \normalsize } } } } \right ) ^ \prime } } = { { \left ( { \sqrt { { x ^ { \large \frac { 3 } { 2 } \normalsize } } } } \right ) ^ \prime } } \\ & = { { \left ( { { { \left ( { { x ^ { \large \frac { 3 } { 2 } \normalsize } } } \right ) } ^ { \large \frac { 1 }{ 2 } \normalsize } } } \right ) ^ \prime } } = { { \left ( { { x ^ { \large \frac { 3 } { 4 } \normalsize } } } \right ) ^ \prime } } = { \frac { 3 } { 4 } { x ^ { \large \frac { 3 } { 4 } \normalsize – 1 } } } = { \frac { 3 } { 4 } { x ^ { – \large \frac { 1 } { 4 } \normalsize } } } = { \frac { 3 } { { 4 \sqrt [ \large 4 \normalsize ] { x } } } . } \end {align*} y ’ ( x ) = ( x x ) ′ = x ⋅ x 2 1 ′ = x 2 3 ′ = ( x 2 3 ) 2 1 ′ = ( x 4 3 ) ′ = 4 3 x 4 3 –1 = 4 3 x – 4 1 = 4 4 x 3 .
مثال ۱۴: مشتق تابع y = x 2 x { y = \sqrt { { x ^ 2 } \sqrt x } } y = x 2 x
حل: ابتدا تابع را به یک تابع توانی تبدیل میکنیم و سپس مشتق رادیکال را به دست میآوریم:
y ( x ) = x 2 x = x 2 ⋅ x 1 2 = x 2 + 1 2 = x 5 2 = ( x 5 2 ) 1 2 = x 5 2 ⋅ 1 2 = x 5 4 . \large \begin {align*} y \left ( x \right ) & = \sqrt { { x ^ 2 } \sqrt x } = \sqrt { { x ^ 2 } \cdot { x ^ { \frac { 1 } { 2 } } } } = { \sqrt { { x ^ { 2 + \frac { 1 } { 2 } } } } } \\ & = { \sqrt { { x ^ { \frac { 5 } { 2 } } } } } = { { \left ( { { x ^ { \frac { 5 } { 2 } } } } \right ) ^ { \frac { 1 } { 2 } } } } ={ { x ^ { \frac { 5 } { 2 } \cdot \frac { 1 } { 2 } } } } = { { x ^ { \frac { 5 } { 4 } } } . } \end {align*} y ( x ) = x 2 x = x 2 ⋅ x 2 1 = x 2 + 2 1 = x 2 5 = ( x 2 5 ) 2 1 = x 2 5 ⋅ 2 1 = x 4 5 .
مثال ۱۵: مشتق رادیکال زیر را به دست آورید.
حل: مشابه مثال قبل، برای محاسبه مشتق رادیکال داریم:
مثال ۱۶: مشتق تابع y = 3 2 x x 3 y = { \large \frac { 3 } { 2 } \normalsize } x \sqrt [ \large 3 \normalsize ] { x } y = 2 3 x 3 x
حل: از تابع به عنوان یک تابع توانی مشتق میگیریم و مشتق رادیکال را خواهیم داشت:
y ’ ( x ) = ( 3 2 x x 3 ) ′ = ( 3 2 x ⋅ x 1 3 ) ′ = 3 2 ( x 1 + 1 3 ) ′ = 3 2 ( x 4 3 ) ′ = 3 2 ⋅ 4 3 x 4 3 – 1 = 2 x 1 3 = 2 x 3 . \large \begin {align*}
y’ \left ( x \right ) & = { \left ( { \frac { 3 } { 2 } x \sqrt [ \large 3 \normalsize ] { x } } \right ) ^ \prime } = { { \left ( { \frac { 3 } { 2 } x \cdot { x ^ { \large \frac { 1 }{ 3 } \normalsize } } } \right ) ^ \prime } } = { \frac { 3 } { 2 }{ \left ( { { x ^ { 1 + \large \frac { 1 } { 3 } \normalsize } } } \right ) ^ \prime } } \\ & = { \frac { 3 } { 2 } { \left ( { { x ^ { \large \frac { 4 } { 3 } \normalsize } } } \right ) ^ \prime } } = { \frac { 3 } { 2 } \cdot \frac { 4 } { 3 } { x ^ { \large \frac { 4 } { 3 } \normalsize – 1 } } } = { 2 { x ^ { \large \frac { 1 } { 3 } \normalsize } } = 2 \sqrt [ \large 3 \normalsize ] { x } . }
\end {align*} y ’ ( x ) = ( 2 3 x 3 x ) ′ = ( 2 3 x ⋅ x 3 1 ) ′ = 2 3 ( x 1 + 3 1 ) ′ = 2 3 ( x 3 4 ) ′ = 2 3 ⋅ 3 4 x 3 4 –1 = 2 x 3 1 = 2 3 x .
مثال ۱۷: مشتق رادیکال f ( x ) = 2 x 2 − 5 f ( x ) = \sqrt { 2 x ^ { 2 } -5 } f ( x ) = 2 x 2 − 5
حل: رادیکال را به صورت توانی زیر مینویسیم:
f ( x ) = ( 2 x 2 − 5 ) 1 / 2 \large f ( x ) = \left ( 2 x ^ { 2 } - 5 \right ) ^ { 1 / 2 } f ( x ) = ( 2 x 2 − 5 ) 1/2
و طبق قانون مشتق توابع توانی، مشتق رادیکال را داریم:
d y d x = 1 2 ( 2 x 2 − 5 ) ( 1 / 2 ) − 1 ( 4 x ) = 1 2 ( 2 x 2 − 5 ) − 1 / 2 ( 4 x ) = 2 x ( 2 x 2 − 5 ) − 1 / 2 = 2 x 2 x 2 − 5 = 2 x 2 x 2 − 5 2 x 2 − 5 \large \begin {aligned}
\frac { d y } { d x } & = \frac { 1 } { 2 } \left ( 2 x ^ { 2 } - 5 \right ) ^ { ( 1 / 2 ) - 1 } ( 4 x ) \\
& = \frac { 1 } { 2 } \left ( 2 x ^ { 2 } - 5 \right ) ^ { - 1 / 2 } ( 4 x ) \\
& = 2 x \left ( 2 x ^ { 2 } -5 \right ) ^ { - 1 / 2 } \\
& = \frac { 2 x } { \sqrt { 2 x ^ { 2 } - 5 } } \\
& = \frac { 2 x \sqrt { 2 x ^ { 2 } -5 } } { 2 x ^ { 2 } - 5 }
\end {aligned} d x d y = 2 1 ( 2 x 2 − 5 ) ( 1/2 ) − 1 ( 4 x ) = 2 1 ( 2 x 2 − 5 ) − 1/2 ( 4 x ) = 2 x ( 2 x 2 − 5 ) − 1/2 = 2 x 2 − 5 2 x = 2 x 2 − 5 2 x 2 x 2 − 5
مثال ۱۸: مشتق تابع f ( x ) = 2 x + 1 3 x 2 + 2 f ( x ) = \frac { 2 x + 1 } { \sqrt { 3 x ^ { 2 } + 2 } } f ( x ) = 3 x 2 + 2 2 x + 1
حل: رادیکال را با یک تابع توانی جایگزین میکنیم:
f ( x ) = 2 x + 1 ( 3 x 2 + 2 ) 1 / 2 \large f ( x ) = \frac { 2 x + 1 } { \left ( 3 x ^ { 2 } + 2 \right ) ^ { 1 / 2 } } f ( x ) = ( 3 x 2 + 2 ) 1/2 2 x + 1
با آوردن مخرج به صورت، توان منفی میشود و داریم:
f ( x ) = ( 2 x + 1 ) ( 3 x 2 + 2 ) − 1 / 2 \large f ( x ) = ( 2 x + 1 ) \left ( 3 x ^ { 2 } + 2 \right ) ^ { - 1 / 2 } f ( x ) = ( 2 x + 1 ) ( 3 x 2 + 2 ) − 1/2
دو مشتق زیر را داریم:
d d x ( 2 x + 1 ) = 2 \large \frac { d } { d x } ( 2 x + 1 ) = 2 d x d ( 2 x + 1 ) = 2
و
d d x ( 3 x 2 + 2 ) − 1 / 2 = − 1 / 2 ( 3 x 2 + 2 ) ( − 1 / 2 ) − 1 ( 6 x ) = − 3 x ( 3 x 2 + 2 ) − 3 / 2 \large \begin {aligned}
\frac { d } { d x } \left ( 3 x ^ { 2 } + 2 \right ) ^ { - 1 / 2 } & = - 1 / 2 \left (3 x ^ { 2 } + 2 \right ) ^ { ( - 1 / 2 ) - 1 } ( 6 x ) \\
& = - 3 x \left ( 3 x ^ { 2 } + 2 \right ) ^ { - 3 / 2 }
\end {aligned} d x d ( 3 x 2 + 2 ) − 1/2 = − 1/2 ( 3 x 2 + 2 ) ( − 1/2 ) − 1 ( 6 x ) = − 3 x ( 3 x 2 + 2 ) − 3/2
اکنون با استفاده از قاعده زنجیرهای مشتق، میتوانیم بنویسیم:
f ( x ) = ( 2 x + 1 ) [ − 3 x ( 3 x 2 + 2 ) − 3 / 2 ] + ( 3 x 2 + 2 ) − 1 / 2 ( 2 ) \large f ( x ) = ( 2 x + 1 ) \left [ - 3 x \left ( 3 x ^ { 2 } + 2 \right ) ^ { - 3 / 2 } \right ] + \left ( 3 x ^ { 2 } + 2 \right ) ^ { - 1 / 2 } ( 2 ) f ( x ) = ( 2 x + 1 ) [ − 3 x ( 3 x 2 + 2 ) − 3/2 ] + ( 3 x 2 + 2 ) − 1/2 ( 2 )
با ضرب طرفین در ( 3 x 2 + 2 ) 3 / 2 \left ( 3 x ^ { 2 } + 2 \right ) ^ { 3 / 2 } ( 3 x 2 + 2 ) 3/2
f ′ ( x ) = − 3 x ( 2 x + 1 ) + 2 ( 3 x 2 + 2 ) ( 3 x 2 + 2 ) 3 / 2 = − 6 x 2 − 3 x + 6 x 2 + 4 ( 3 x 2 + 2 ) 3 / 2 = 4 − 3 x ( 3 x 2 + 2 ) 3 / 2 \large \begin {aligned} f ^ { \prime } ( x ) & = \frac { - 3 x ( 2 x + 1 ) + 2 \left ( 3 x ^ { 2 } + 2 \right ) } { \left ( 3 x ^ { 2 } + 2 \right ) ^ { 3 / 2 } } \\ & = \frac { - 6 x ^ { 2 } - 3 x + 6 x ^ { 2 } + 4 } { \left ( 3 x ^ { 2 } + 2 \right ) ^ { 3 / 2 } } \\ & = \frac { 4 - 3 x } { \left ( 3 x ^ { 2 } + 2 \right ) ^ { 3 / 2 } } \end {aligned} f ′ ( x ) = ( 3 x 2 + 2 ) 3/2 − 3 x ( 2 x + 1 ) + 2 ( 3 x 2 + 2 ) = ( 3 x 2 + 2 ) 3/2 − 6 x 2 − 3 x + 6 x 2 + 4 = ( 3 x 2 + 2 ) 3/2 4 − 3 x
مثال ۱۹: مشتق تابع 625 − x 2 / x \sqrt { 6 2 5 - x ^ { 2 } } / \sqrt { x } 625 − x 2 / x
حل: به دو روش میتوان این مشتق رادیکال را حل کرد. اولی استفاده از قاعده خارج قسمت است:
d d x 625 − x 2 x = x ( − x / 625 − x 2 ) − 625 − x 2 ⋅ 1 / ( 2 x ) x \large \frac { d } { d x } \frac { \sqrt { 6 2 5 - x ^ { 2 } } } { \sqrt { x } } = \frac { \sqrt { x } ( - x / \sqrt { 6 2 5 - x ^ { 2 } } ) - \sqrt { 6 2 5 - x ^ { 2 } } \cdot 1 / ( 2 \sqrt { x } ) } { x } d x d x 625 − x 2 = x x ( − x / 625 − x 2 ) − 625 − x 2 ⋅ 1/ ( 2 x )
روش دوم نیز استفاده از قاعده مشتق ضرب دو تابع است:
d d x 625 − x 2 x − 1 / 2 = 625 − x 2 − 1 2 x − 3 / 2 + − x 625 − x 2 x − 1 / 2 \large \frac { d } { d x } \sqrt { 6 2 5 - x ^ { 2 } } x ^ { - 1 / 2 } = \sqrt { 6 2 5 - x ^ { 2 } } \frac { - 1 } { 2 } x ^ { - 3 / 2 } + \frac { - x } { \sqrt { 6 2 5 - x ^ { 2 } } } x ^ { - 1 / 2 } d x d 625 − x 2 x − 1/2 = 625 − x 2 2 − 1 x − 3/2 + 625 − x 2 − x x − 1/2
با کمی سادهسازی، جواب نهایی مشتق رادیکال برای دو روش به دست خواهد آمد:
− x 2 + 625 2 625 − x 2 x 3 / 2 \large - \frac { x ^ { 2 } + 6 2 5 } { 2 \sqrt { 6 2 5 - x ^ { 2 } } x ^ { 3 / 2 } } − 2 625 − x 2 x 3/2 x 2 + 625
مثال ۲۰: مشتق رادیکال 1 + 1 + x \sqrt { 1 + \sqrt { 1 + \sqrt { x } } } 1 + 1 + x
حل: دو تابع g ( x ) = 1 + 1 + x g ( x ) = 1 + \sqrt { 1 + \sqrt { x } } g ( x ) = 1 + 1 + x f ( x ) = x f ( x ) = \sqrt { x } f ( x ) = x
d d x 1 + 1 + x = 1 2 ( 1 + 1 + x ) − 1 / 2 d d x ( 1 + 1 + x ) \large \frac { d } { d x } \sqrt { 1 + \sqrt { 1 + \sqrt { x } } } = \frac { 1 } { 2 } ( 1 + \sqrt { 1 + \sqrt { x } } ) ^ { - 1 / 2 } \frac { d } { d x } ( 1 + \sqrt { 1 + \sqrt { x } } ) d x d 1 + 1 + x = 2 1 ( 1 + 1 + x ) − 1/2 d x d ( 1 + 1 + x )
اکنون باید مشتق 1 + x \sqrt{1+\sqrt{x}} 1 + x
d d x 1 + x = 1 2 ( 1 + x ) − 1 / 2 1 2 x − 1 / 2 \large \frac { d } { d x } \sqrt { 1 + \sqrt { x } } = \frac { 1 } { 2 } ( 1 + \sqrt { x } ) ^ { - 1 / 2 } \frac { 1 } { 2 } x ^ { - 1 / 2 } d x d 1 + x = 2 1 ( 1 + x ) − 1/2 2 1 x − 1/2
در نهایت، حاصل مشتق رادیکال اصلی به شکل زیر خواهد بود:
d d x 1 + 1 + x = 1 2 ( 1 + 1 + x ) − 1 / 2 1 2 ( 1 + x ) − 1 / 2 1 2 x − 1 / 2 = 1 8 x 1 + x 1 + 1 + x \large \begin {aligned}
\frac { d } { d x } \sqrt { 1 + \sqrt { 1 + \sqrt { x } } } & = \frac { 1 } { 2 } ( 1 + \sqrt { 1 + \sqrt { x } } ) ^ { - 1 / 2 } \frac { 1 } { 2 } ( 1 + \sqrt { x } ) ^ { - 1 / 2 } \frac { 1 } { 2 } x ^ { - 1 / 2 } \\
& = \frac { 1 } { 8 \sqrt { x } \sqrt { 1 + \sqrt { x } } \sqrt { 1 + \sqrt { 1 + \sqrt { x } } } }
\end {aligned} d x d 1 + 1 + x = 2 1 ( 1 + 1 + x ) − 1/2 2 1 ( 1 + x ) − 1/2 2 1 x − 1/2 = 8 x 1 + x 1 + 1 + x 1





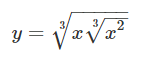
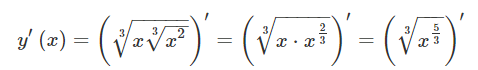
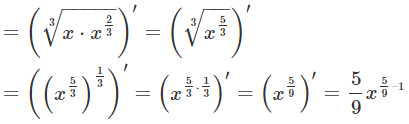
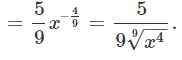














مطالب خیلی خوب و عالی بود ممنونم از شما❤
عالی بود خیلی ممنونم از مجله فرادرس❤