کاربرد‌ها، روش‌ های محاسبه و مفاهیم مشتق — مجموعه مقالات وبلاگ فرادرس

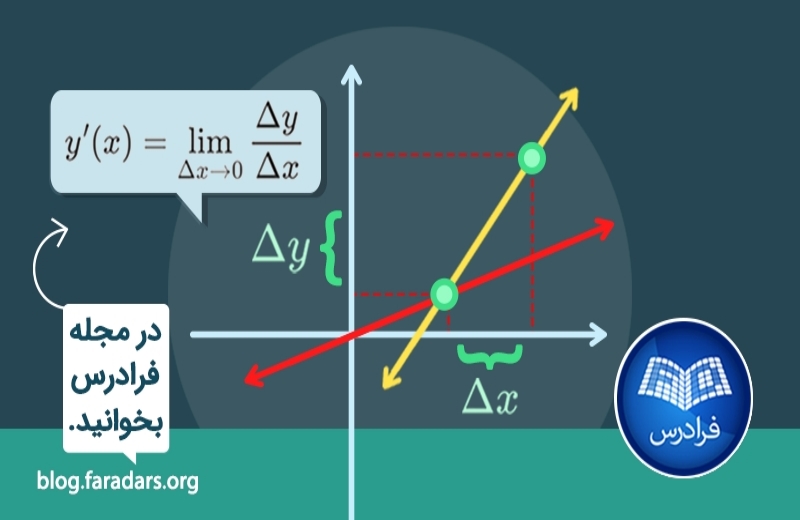
به جرأت می‌توان گفت که با ارائه مفهوم مشتق در ریاضی، نه تنها این علم بلکه تمامی علوم تحت تاثیر آن قرار گرفتند. معمولاً وقوع یک پدیده در طبیعت برخواسته از تغییرات مشخصه‌هایی از آن است. بنابراین به منظور مطالعه پدیده‌های تازه به وقع پیوسته نیازمند بررسی تغییرات مشخصه‌های عامل آن هستیم. تمامی این تغییرات با استفاده از مفاهیم مشتق مورد بررسی قرار می‌گیرند. در همین راستا و طی مقالات پیشین مجله فرادرس به جنبه‌های مختلف این مفهوم، یعنی مشتق پرداخته‌ایم و روش‌های محاسبه و کاربردهای آن را توضیح داده‌ایم. آنچه در ادامه آمده، جمع‌بندی و فهرستی از این مجموعه مقالات در رابطه با مشتق است.

مفاهیم مشتق

مشتق در حقیقت شیب نمودار تابع $$f ( x )$$ در یک نقطه است. در ابتدا دو نقطه از یک تابع را مطابق با شکل زیر در نظر بگیرید.

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

اگر این دو نقطه را به یکدیگر متصل کنیم، خطی حاصل می‌شود که دارای شیب مشخصی است. با ثابت نگه داشتن نقطه اول و نزدیک کردن تدریجی نقطه دوم به آن، شیب خط نیز تغییر می‌کند. اما شیب دقیق در نقطه $$x$$ زمانی بدست می‌آید که دو نقطه به فاصله بسیار اندکی از یکدیگر قرار گرفته باشند.

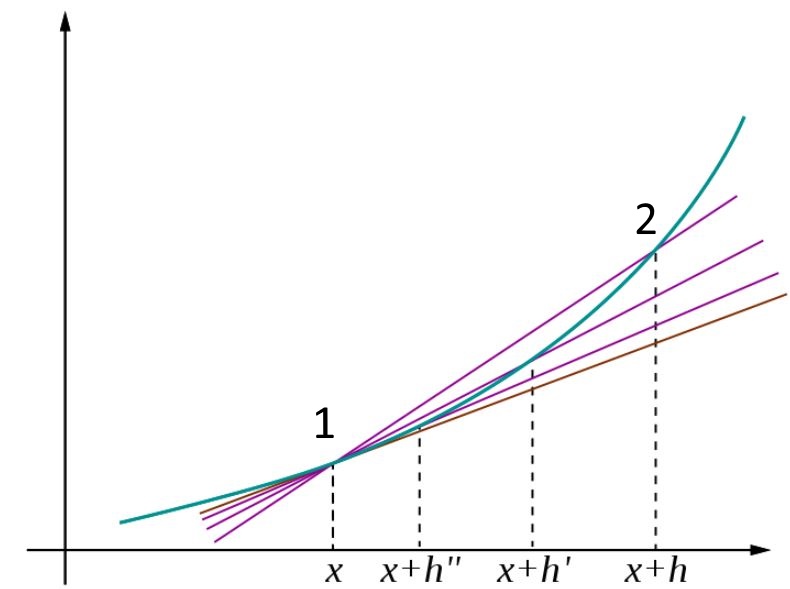
برای نمونه اندازه شیب بین دو نقطه ۱ و ۲ برابر است با:

$$\large m = \frac { f ( x + h ) - f ( x ) } { h }$$

حال اگر فاصله بین دو نقطه را بسیار اندک در نظر بگیریم، شیب دقیق در نقطه اول بدست می‌آید که برابر با همان مشتق در نقطه اول است. بنابراین مشتق تابع $$f(x)$$ در نقطه اول (یا همان $$x$$) برابر است با:

$$\large f ^ { \prime } ( x ) =\lim _ { h \to 0 } \frac { f ( x + h ) - f ( x ) } { h }$$

عبارت فوق پایه‌ای‌ترین بیانِ مشتق محسوب می‌شود. اما این مفهوم برای توابع دومتغیره و دیگر توابع نیز قابل تعریف هستند. در ادامه مجموعه مقالات تهیه شده به‌منظور توضیح مفاهیم مرتبط با مشتق ارائه شده‌اند.

• مشتق — به زبان ساده
• مشتق ضمنی — به زبان ساده
• مشتق جزئی — به زبان ساده
• مشتق توابع پارامتری — از صفر تا صد
• مشتق در مختصات قطبی — به زبان ساده
• فرمول لایب نیتس برای مشتق — به زبان ساده

روش‌های محاسبه مشتق

توجه داشته باشید که تعریف کلی مشتق مطابق با رابطه فوق است. با این حال برای برخی از توابع، استفاده از تعریف به‌منظور محاسبه مشتق دشوار است.

فیلم آموزش ریاضی عمومی 2 – جامع و کاربردی در فرادرس

کلیک کنید

از این رو در ادامه مجموعه مقالات ارائه شده به‌منظور محاسبه مشتق توابع مختلف، آورده شده‌اند.

• روش‌های مشتق‌گیری — به همراه مثال
• مشتق زنجیره ای — به زبان ساده
• تقلب نامه (Cheat Sheet) فرمول‌ های مشتق گیری
• مشتق جهتی یا مشتق سویی — از صفر تا صد
• مشتق لگاریتم و تابع نمایی — از صفر تا صد
• مشتق توابع هذلولوی و معکوس آن‌ها — از صفر تا صد
• مشتق توابع معکوس مثلثاتی — به زبان ساده
• مشتق توابع معکوس — از صفر تا صد

کاربرد‌های مشتق

همان‌طور که در ادامه این مطلب نیز بیان شد، مفاهیم مشتق نقشی پررنگ را در بسیاری از علوم ایفا می‌کنند. حتی می‌توان علوم انسانی و اقتصاد را با استفاده از مفاهیم ریاضیاتی، فرمول‌بندی کرد.

فیلم آموزش ریاضی عمومی ۲ – مرور و حل تمرین در فرادرس

کلیک کنید

در ادامه مقالاتی ارائه شده که در آن‌ها مهم‌ترین کاربرد‌های مشتق ارائه شده‌اند.

• ماکزیمم و مینیمم تابع — به زبان ساده
• قاعده هوپیتال — به زبان ساده
• اکسترمم مطلق — به زبان ساده
• اثبات نامساوی با مشتق — به زبان ساده
• کاربرد مشتق — به زبان ساده
• نرخ تغییرات در ریاضی — به زبان ساده
• مشتق و انتگرال سری توانی — به زبان ساده
• دیفرانسیل تابع — به زبان ساده

احتمالا با توجه به زمان موجود، امکان توضیح تمامی مفاهیم مشتق وجود ندارد. با این حال تیم وبلاگ فرادرس در تلاش است تا بتواند گستره بیشتری از مطالب مرتبط با مشتق را پوشش دهد. لذا توجه داشته باشید که لیست‌های ارائه شده در این مطلب با گذشت زمان بروزرسانی خواهند شد.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضی و فیزیک
• مجموعه آموزش‌های دروس دبیرستان
• مفاهیم، روش‌های محاسبه و کاربردهای انتگرال -- مجموعه مقالات وبلاگ فرادرس
• فهرست مطالب ریاضی وبلاگ فرادرس
• مشتق - به زبان ساده

^^