قاعده مثلث چیست و چگونه بدست می آید؟ + تعریف و مثال

قاعده، ضلعی است که به منظور تعیین مساحت مثلث مورد استفاده قرار میگیرد. تعریف قاعده مثلث و روشهای محاسبه آن، به نوع مثلث (قائم الزاویه، متساوی الاضلاع، متساوی الساقین یا مختلف الاضلاع بودن مثلث) بستگی دارد. در این مقاله از مجله فرادرس، به معرفی قاعده در انواع مثلث و نحوه محاسبه آن با استفاده از ارتفاع، مساحت، محیط و روابط مثلثاتی میپردازیم.
مثلث چیست؟
مثلث، یکی از شکلهای هندسی پایه و از پرکاربردترین انواع چند ضلعی است. مثلثها از سه ضلع تشکیل میشوند. تصویر زیر، نمونهای از یک مثلث مختلف الاضلاع را نمایش میدهد.
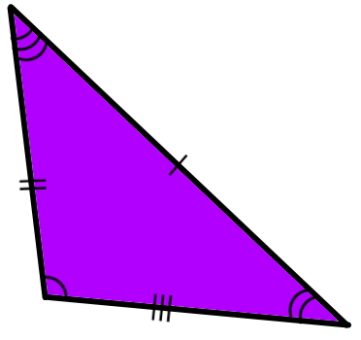
اجزای مثلث چه هستند؟
هر مثلث، از اجزای مختلفی مانند راس، ضلع، زاویه داخلی، زاویه خارجی و ارتفاع تشکیل میشود:
- راس: محل برخورد دو ضلع مثلث
- ضلع: پاره خط بین دو راس
- زاویه داخلی: زاویه بین دو ضلع مجاور
- زاویه خارجی: زاویه بین ضلع با امتداد ضلع مجاور (زاویه مکمل)
- ارتفاع: پاره خط عمود بر ضلع (فاصله عمودی از هر راس تا ضلع مقابل)
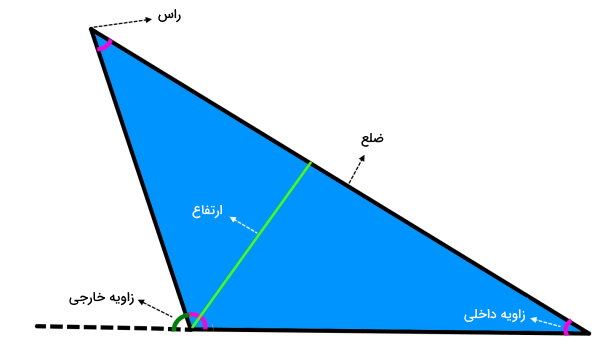
مثلثها، دارای سه ضلع، سه راس، سه زاویه داخلی، سه زاویه خارجی و سه ارتفاع هستند. ضلع و ارتفاع، معمولا به منظور محاسبه مساحت مثلث مورد استفاده قرار میگیرند. علاوه بر این، زوایای داخلی نیز کاربرد گستردهای در تعیین مساحت و اندازه ضلعها دارند.
قاعده در مثلث چیست ؟
قاعده (به انگلیسی Base)، یکی اجزای اشکال هندسی دو بعدی است که در اندازهگیریها و محاسبات این اشکال به کار برده میشود. قاعده در مثلث، همان ضلع مورد استفاده برای محاسبه مساحت است. تصویر زیر، قاعدههای یک مثلث مختلف الاضلاع را با حروف فارسی الف، ب و پ نمایش میدهد.
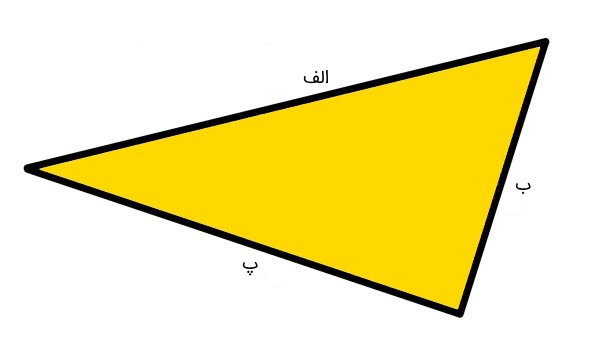
رابطه بین مساحت، ارتفاع و قاعده مثلث، به صورت زیر نوشته میشود:
۲ ÷ (قاعده ارتفاع) = مساحت مثلث
فرمول ریاضی مساحت مثلث، عبارت است از:
- A: مساحت
- h: ارتفاع
- b: قاعده نظیر ارتفاع
بر اساس فرمول بالا، هر سه ضلع مثلث را میتوان به عنوان قاعده در نظر گرفت. البته برای محاسبه مساحت، باید از ارتفاع نظیر آن قاعده استفاده کرد. به همین ترتیب، در صورت مشخص بودن مساحت و ارتفاع، امکان تعیین قاعده نظیر فراهم میشود.
قاعده نظیر مثلث چیست؟
به ضلعی که یکی از ارتفاعهای مثلث بر آن عمود میشود، قاعده نظیر آن ارتفاع میگویند. هر مثلث دارای سه جفت ارتفاع و قاعده است. عبارت «نظیر»، برای اشاره به هر یک از این جفتها مورد استفاده قرار میگیرد. به عنوان مثال، در تصویر زیر، ضلعها و خطچینهای هم رنگ، قاعده و ارتفاع نظیر یکدیگر هستند.
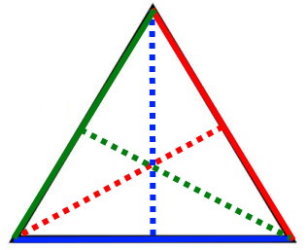
نحوه تعیین قاعده نظیر به نوع مثلث و اندازههای معلوم آن بستگی دارد. در ادامه به معرفی روشهای عمومی و اختصاصی برای محاسبه انواع مثلثها میپردازیم.
قاعده مثلث مختلف الاضلاع چگونه بدست می آید ؟
مثلث مختلف الاضلاع، مثلثی با سه ضلع متفاوت است. قاعده این مثلث با استفاده از فرمول کلی مساحت به دست میآید. مطابق با فرمول مساحت مثلث بر اساس ارتفاع و قاعده نظیر، داریم:
اگر فرمول بالا را بر حسب قاعده (b) بازنویسی کنیم، به فرمول قاعده بر اساس مساحت و ارتفاع میرسیم:
به این ترتیب، در صورت معلوم بودن مساحت و هر یک از ارتفاعهای مثلث، امکان تعیین مستقیم قاعده نظیر آن ارتفاع توسط فرمول بالا فراهم میشود.
مثال اول: محاسبه قاعده مثلث با ارتفاع و مساحت
مثلثی با مساحت 7 سانتیمتر مربع و ارتفاع 4 سانتیمتر را در نظر بگیرید. یکی از قاعدههای این مثلث را حساب کنید.
به دلیل مشخص بودن اندازه مساحت و یکی از ارتفاعهای مثلث، میتوان قاعده نظیر آن ارتفاع معلوم را با استفاده از رابطه زیر به دست آورد:
- b: قاعده نظیر ارتفاع معلوم
- A: مساحت مثلث برابر 7 سانتیمتر مربع
- h: ارتفاع نظیر قاعده برابر 4 سانتیمتر
اندازههای معلوم را درون فرمول بالا قرار میدهیم:
قاعده نظیر ارتفاع 4 سانتیمتری مثلث، برابر 3/5 سانتیمتر است. برای اطمینان از درست بودن نتیجه، این دو عدد را در یکدیگر ضرب و تقسیم بر دو کنید تا مساحت مثلث به دست بیاید.
قاعده در مثلث قائم الزاویه
مثلث قائم الزاویه، مثلثی با یک زاویه 90 درجه است. ضلعهای تشکیل دهنده زاویه قائمه، با عنوان «ساق» و ضلع سوم، با عنوان «وتر» شناخته میشود. به دلیل عمود بودن ساقها، این دو ضلع، قاعده و ارتفاع نظیر یکدیگر هستند.
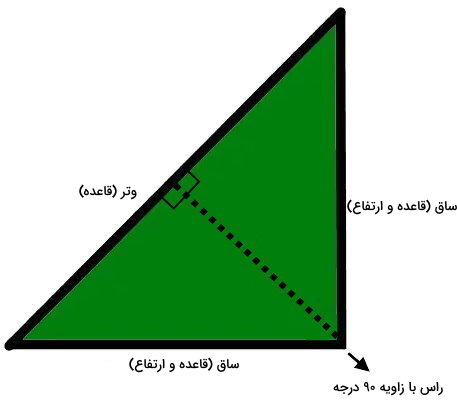
مثلثهای قائم الزاویه، از قضیه فیثاغورس پیروی میکنند. بر اساس این قضیه، رابطه زیر بین اندازه ضلعهای مثلث قائم الزاویه برقرار است:
- c: وتر مثلث قائم الزاویه
- a: یکی از ساقهای مثلث
- b: ساق دیگر مثلث
به این ترتیب، اگر دو قاعده مثلث قائم الزاویه معلوم باشد، قاعده سوم با استفاده از فرمول بالا به دست میآید.
مثال دوم: محاسبه هر سه قاعده مثلث قائم الزاویه با یک ضلع و مساحت
اندازه هر سه قاعده در مثلث قائم الزاویه زیر را حساب کنید.
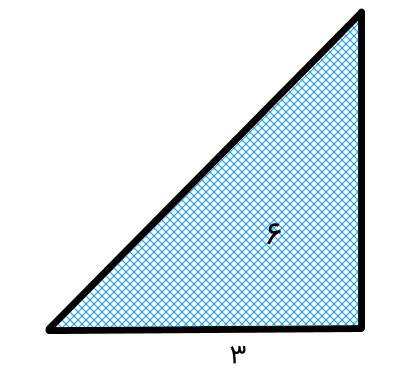
در مثلث قائم الزاویه بالا، اندازه یکی از ساقها و مساحت داده شده است. از آنجایی که ساقهای این مثلث، ارتفاع و قاعده نظیر یکدیگر هستند، فرمول کلی مساحت بر اساس اندازه ساقها را مینویسیم:
- A: مساحت مثلث برابر 6
- h: ارتفاع برابر 3 (اندازه یکی از ساقها)
- b: قاعده نظیر ارتفاع برابر اندازه ساق دیگر
فرمول کلی قاعده را مینویسیم و اندازههای معلوم را درون آن قرار میدهیم:
در نتیجه، اندازه ساق دیگر مثلث (یکی دیگر از قاعدهها)، برابر 4 است. اکنون، اندازه دو قاعده مثلث قائم الزاویه را داریم. به این ترتیب، اندازه قاعده سوم (وتر) را توسط قضیه فیثاغورس به دست میآوریم:
- c: وتر مثلث قائم الزاویه
- a: اندازه یکی از ساقها برابر 3
- b: اندازه ساق دیگر برابر 4
در نتیجه، اندازه قاعده سوم یا همان وتر مثلث برابر 5 است.
قاعده در مثلث متساوی الساقین
تعریف قاعده در مثلث متساوی الساقین با دیگر انواع مثلث کمی تفاوت دارد. مثلث متساوی الساقین، از دو ضلع و دو زاویه برابر تشکیل میشود. به ضلعهای برابر این مثلث، «ساق» میگویند. ضلع سوم، با عنوان «قاعده» شناخته میشود. به همین دلیل، منظور از ارتفاع مثلث متساوی الساقین، معمولا همان ارتفاع نظیر قاعده (ضلع سوم) است.
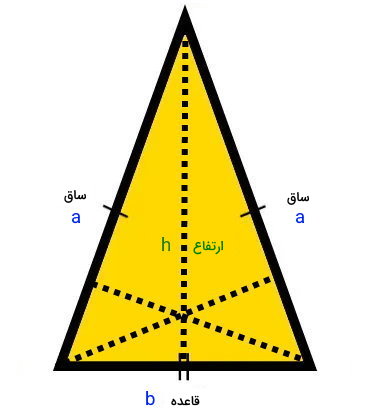
در صورت رسم ارتفاع، مثلث متساوی الساقین به دو مثلث قائم الزاویه تبدیل میشود. وتر این دو مثلث، برابر ساق مثلث متساوی الساقینها و ساق پایینی آنها، برابر نصف قاعده مثلث متساوی الساقین است. اگر قضیه فیثاغورس را برای یکی از مثلثهای قائم الزاویه بنویسیم و رابطه به دست آمده را بر حسب قاعده بازنویسی کنیم، به فرمول زیر میرسیم:
- b: قاعده مثلث متساوی الساقین
- a: ساق مثلث متساوی الساقین
- h: ارتفاع مثلث متساوی الساقین
فرمول بالا، به منظور محاسبه مستقیم قاعده مثلث متساوی الساقین بر اساس اندازه ساق و ارتفاع مورد استفاده قرار میگیرد.
قاعده در مثلث متساوی الساقین قائم الزاویه
یکی از حالتهای خاص مثلث متساوی الساقین، وجود زاویه 90 درجه بین دو ساق است. در این حالت، فقط با دانستن اندازه یکی از ضلعها یا مساحت، میتوان اندازه تمام قاعدهها را به دست آورد.

در مثلث بالا، رابطه بین ساق (a) و وتر (c) به صورت زیر است:
یا
در مثلث متساوی الساقین قائم الزاویه، رابطه بین اندازه ساق و مساحت (A) به صورت زیر نوشته میشود:
محاسبه اندازه وتر با استفاده از مساحت نیز توسط رابطه زیر انجام میگیرد:
مثال سوم: محاسبه قاعده مثلث متساوی الساقین با ساق و ارتفاع
قاعده مثلث متساوی الساقین با ساقهای 13 سانتیمتر و ارتفاع 12 سانتیمتر را حساب کنید.
مطابق با فرمول قاعده مثلثهای متساوی الساقین بر حسب ساق و ارتفاع، داریم:
- b: قاعده
- a: اندازه ساق برابر 13 سانتیمتر
- h: اندازه ارتفاع برابر 12 سانتیمتر
اندازه قاعده (ضلع سوم) مثلث برابر با 10 سانتیمتر است.
قاعده در مثلث متساوی الاضلاع
مثلث متساوی الاضلاع، مثلثی با سه ضلع برابر است. برابر بودن اندازه ضلعها، امکان محاسبه قاعدههای این مثلث را با استفاده از مساحت یا ارتفاع فراهم میکند.
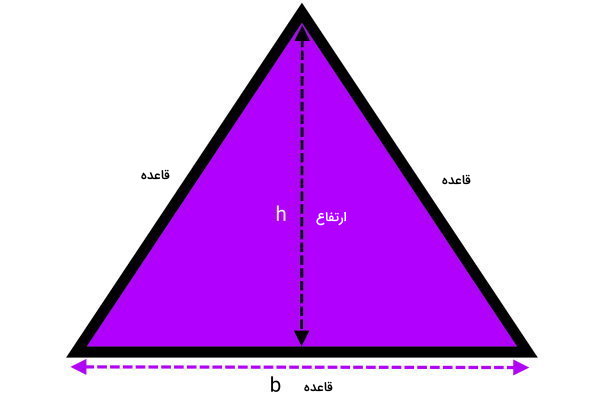
فرمول مساحت مثلث متساوی الاضلاع به صورت زیر نوشته میشود:
- A: مساحت مثلث
- a: اندازه ضلع مثلث
به این ترتیب، در صورت مشخص بودن مساحت، میتوان اندازه قاعده مثلث متساوی الاضلاع را با استفاده از فرمول زیر محاسبه کرد:
علاوه بر این، رابطه بین ارتفاع و ضلع مساحت مثلث متساوی الاضلاع عبارت است از:
- h: اندازه ارتفاع مثلث
- a: اندازه ضلع مثلث
با بازنویسی رابطه بالا بر حسب ضلع (a)، امکان تعیین قاعده مثلث متساوی الاضلاع بر اساس ارتفاع فراهم میشود:
قاعده در مثلث با زاویه باز
مثلث با زاویه باز یا مثلث منفرجه، دارای یک زاویه بزرگتر از 90 درجه است. به همین دلیل، دو ارتفاع این مثلث در خارج از محدوده ضلعها قرار میگیرند. مطابق با تصویر زیر، رسم دو ارتفاع خارجی در مثلث منفرجه، بر روی امتداد ضلعهای متصل به زاویه باز انجام میشود.
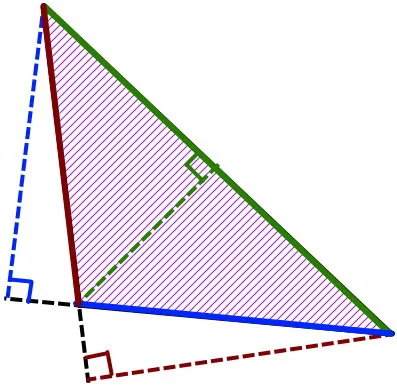
توجه داشته باشید که اندازه بخش امتداد یافته، هیچ تاثیری بر روی محاسبه مساحت مثلث ندارد. به عبارت دیگر، در این حالت نیز، اندازه ضلع همان اندازه قاعده است.
محاسبه قاعده مثلث با قانون سینوس ها
یکی از دیگر روشهای محاسبه قاعده انواع مثلثها، استفاده از اندازه زاویه راسها و روابط مثلثاتی، مخصوصا قانون سینوسها است. به منظور آشنایی با این روش، مثلث زیر را در نظر بگیرید.
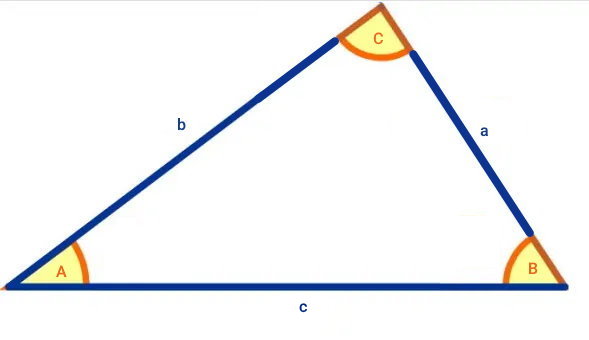
بین اندازه ضلعها و زوایای مثلث بالا، رابطه زیر برقرار است:
- a: طول ضلع BC
- b: طول ضلع AC
- c: طول ضلع AB
- A: زاویه راس A
- B: زاویه راس B
- C: زاویه راس C
به رابطه بالا، قانون سینوسها میگویند. به این ترتیب، اگر اندازه زوایای مثلث و یکی از قاعدههای آن مشخص باشد، اندازه دو قاعده دیگر با استفاده از این قانون به دست میآید.
محاسبه قاعده مثلث با مساحت و سینوس
در مثلثهایی با دو ضلع و زاویه بین معلوم، معمولا از فرمول زیر برای محاسبه مساحت استفاده میشود:
به فرمولهای بالا، فرمول مساحت مثلث با سینوس میگویند. از این فرمولها نیز میتوان در کنار قانون سینوسها برای محاسبه اندازه قاعدههای مثلث استفاده کرد. به عنوان مثال، اگر مساحت مثلث، قاعده b و زاویه C معلوم باشند، قاعده a از فرمول زیر به دست میآید:
- a: قاعده مجهول
- Area: مساحت مثلث
- b: قاعده معلوم
- C: زاویه بین قاعده معلوم و مجهول
مثال چهارم: محاسبه قاعده مثلث با دو زاویه و یک ضلع
در مثلث زیر، اندازه دو زاویه و ضلع بین آنها مشخص شده است. اندازه قاعدههای این مثلث را تعیین کنید. (سینوس زاویه 45 درجه را برابر 0/71، سینوس زاویه 60 درجه را برابر 0/87 و سینوس زاویه 75 درجه را برابر 0/97 در نظر بگیرید.)
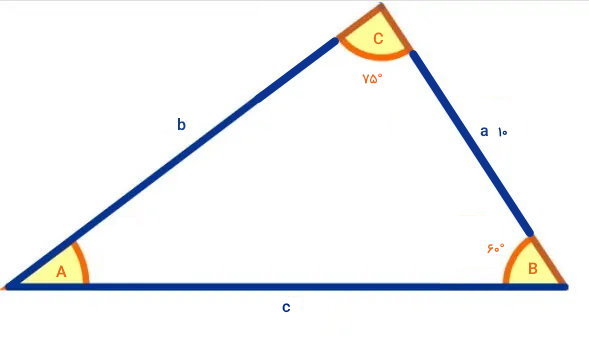
برای شروع حل مسئله، ابتدا قانون سینوسها را مینویسیم و اندازههای معلوم را درون آن قرار میدهیم:
- a: طول قاعده BC برابر 10
- b: طول قاعده AC
- c: طول قاعده AB
- A: زاویه راس A
- B: زاویه راس B برابر 60 درجه
- C: زاویه راس C برابر 75 درجه
همانطور که مشاهده میکنید، اطلاعات ما برای استفاده از قانون سینوسها کافی نیست. برای انجام ادامه محاسبات، به اندازه حداقل یک زاویه یا حداقل یک قاعده دیگر نیاز داریم. مطابق با اصل جمع زوایای داخلی، مجموع زوایای داخلی مثلثها باید برابر 180 درجه باشد. به این ترتیب، داریم:
زاویه سوم را به قانون سینوسها اضافه میکنیم:
اکنون میتوانیم اندازه دو قاعده دیگر را به دست بیاوریم:
اندازه قاعده AC یا b برابر است با:
اندازه قاعده AB یا c نیز به صورت زیر محاسبه میشود:
اندازه قاعده AB برابر 13/66، قاعده AC برابر 12/25 و قاعده BC برابر 10 است.
محاسبه قاعده مثلث با محیط
محیط مثلث، مجموع اندازه ضلعهای آن است. به همین دلیل، در صورت معلوم بودن محیط و اندازه دو قاعده، امکان تعیین قاعده سوم فراهم میشود. البته در مثلثهای خاص (قائم الزاویه، متساوی الساقین، متساوی الاضلاع)، اندازههای مورد نیاز برای تعیین قاعده مجهول کمتر هستند.
فرمول کلی محاسبه قاعده مثلث با محیط عبارت است از:
- P: محیط مثلث
- a: اندازه قاعده اول
- b: اندازه قاعده دوم
- c: اندازه قاعده سوم
قاعده مثلث متساوی الساقین با محیط و ارتفاع
در مثلثهای متساوی الساقین، در صورت مشخص بودن محیط و ارتفاع نظیر قاعده، میتوان اندازه ساقها را با استفاده از فرمول زیر محاسبه کرد:
- a: اندازه ساق
- P: محیط مثلث
- hb: ارتفاع نظیر قاعده
اگر اندازه محیط و قاعده معلوم باشند، فرمول زیر برای محاسبه دو قاعده دیگر مورد استفاده قرار میگیرد:
- a: اندازه ساقها
- P: محیط مثلث
- b: قاعده
قاعده مثلث قائم الزاویه با محیط و ساق
در صورت مشخص بودن محیط و اندازه یکی از ساقهای مثلث قائم الزاویه، اندازه ساق دوم توسط فرمول زیر به دست میآید:
- a: اندازه یکی از ساقها
- P: محیط مثلث
- b: اندازه ساق دیگر
با مشخص شدن اندازه ساق دوم، میتوان اندازه وتر (قاعده سوم) را نیز توسط قضیه فیثاغورس محاسبه کرد. اگر به جای محیط و ساق، محیط و وتر معلوم باشند، فرمولهای محاسبه دو قاعده دیگر، پیچیده میشوند. در بخش جدول فرمولهای قاعده مثلث، به این فرمولها اشاره میکنیم.
قاعده مثلث متساوی الاضلاع با محیط
در صورت مشخص بودن محیط مثلث متساوی الاضلاع، اندازه قاعدههای آن با تقسیم محیط بر سه تعیین میشود:
- a: اندازه قاعدهها
- P: محیط مثلث
مثال پنجم: محاسبه قاعده مثلث با محیط و ارتفاع
اگر محیط مثلث زیر برابر 30 سانتیمتر باشد، اندازه هر سه قاعده این مثلث را به دست بیاورید.
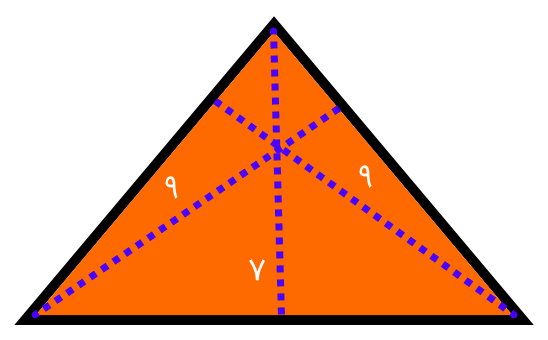
به دلیل هم اندازه بودن دو ارتفاع مثلث بالا، این مثلث از نوع متساوی الساقین است. در نتیجه، اندازه ساقهای این مثلث از رابطه زیر به دست میآید:
- a: اندازه ساق
- P: محیط مثلث برابر 30 سانتیمتر
- hb: ارتفاع نظیر قاعده برابر 7 سانتیمتر
به این ترتیب، اندازه دو قاعده مثلث برابر 9/13 سانتیمتر است. اندازه قاعده سوم، از رابطه کلی زیر به دست میآید:
- P: محیط مثلث برابر 30 سانتیمتر
- a: اندازه قاعده اول برابر 9/13 سانتیمتر
- b: اندازه قاعده دوم برابر 9/13 سانتیمتر
- c: اندازه قاعده سوم
در نتیجه، اندازه قاعده سوم مثلث برابر 11/74 سانتیمتر خواهد بود.
جدول فرمول قاعده مثلث
جدول زیر، برخی از فرمولهای مورد استفاده برای تعیین قاعده مثلث را بر اساس نوع مثلث و اندازههای معلوم نمایش میدهد.
| نوع مثلث | اندازههای معلوم | فرمول محاسبه قاعده مثلث |
| تمام مثلثها | مساحت (A) و ارتفاع (h) | |
| تمام مثلثها | سه زاویه (B ،A و C) و یک ضلع (b ،a یا c) | |
| تمام مثلثها | محیط (P) و اندازه دو ضلع (a و b) | |
| مثلث قائم الزاویه | اندازه دو ضلع (ساق a، ساق b و یا وتر c) | |
| محیط (P) و ساق (b) | ||
| محیط (P) و وتر (c) | ||
| مثلث متساوی الساقین | اندازه یکی از ساقها (a) و ارتفاع نظیر قاعده (hb) | |
| محیط (P) و ارتفاع نظیر قاعده (hb) | ||
| محیط (P) و قاعده (b) | ||
| مثلث متساوی الساقین قائم الزاویه | ساق (a) یا وتر (c) |
|
| مساحت (A) |
| |
| مثلث متساوی الاضلاع | مساحت (A) |
|
| ارتفاع (h) |
| |
| محیط (P) |
|
محاسبه آنلاین قاعده مثلث
یکی از روشهای پیدا کردن اندازه قاعده انواع مثلثها، استفاده ابزارهای اینترنتی و سایتهای تخصصی است. موتور جستجوی Google (+)، سایت Omni Calculator (+) و Calculator.net (+)، از شناخته شدهترین و کاربردیترین ابزارهای محاسبه آنلاین قاعده مثلث هستند.
تصویر زیر، ابزار موتور جستجوی گوگل برای محاسبه اندازهای مختلف یک مثلث نظیر مساحت، محیط، قاعده، ارتفاع و غیره را نمایش میدهد.
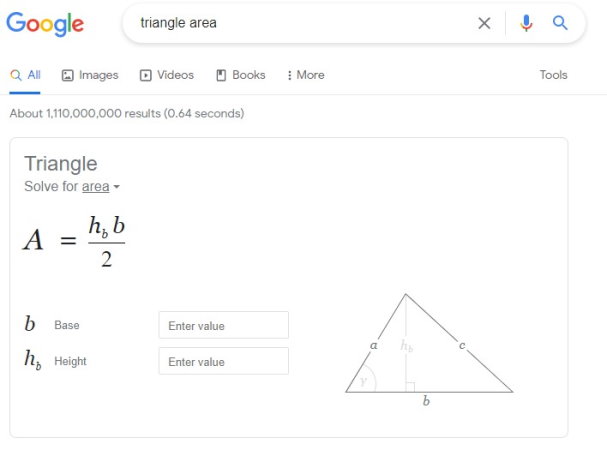
به منظور دسترسی به ماشین حساب مثلث در موتور جستجوی گوگل، عبارتهایی نظیر «triangle area» یا «triangle perimeter» را درون کادر جستجو تایپ کرده و کلید Enter را فشار دهید. با این کار، کادری مشابه تصویر بالا در ابتدای صفحه نتایج ظاهر میشود. با کلیک بر روی فلش رو به پایین در بخش «Solve for» میتوانید اندازه مورد نظر خود برای محاسبه را انتخاب کنید.
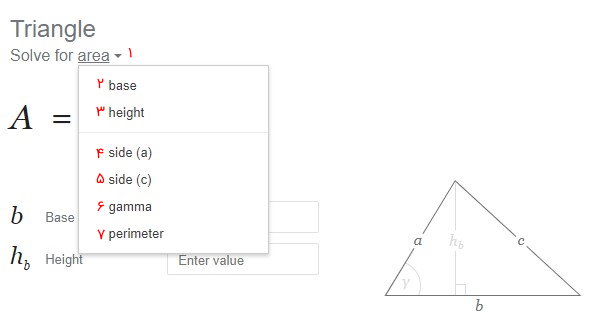
اعداد نمایش داده شده در تصویر بالا، گزینههای مرتبط با مثلث سمت راست هستند:
- Solve for: اندازه قابل محاسبه در این بخش نمایش داده میشود. در این مثال، ماشین حساب گوگل بر روی گزینه «area» برای محاسبه مساحت مثلث قرار دارد.
- base: قاعده
- height: ارتفاع نظیر ضلع یا قاعده b
- side (a): ضلع یا قاعده a
- side (c): ضلع یا قاعده c
- gamma: اندازه زاویه بین دو قاعده a و b
- perimeter: محیط
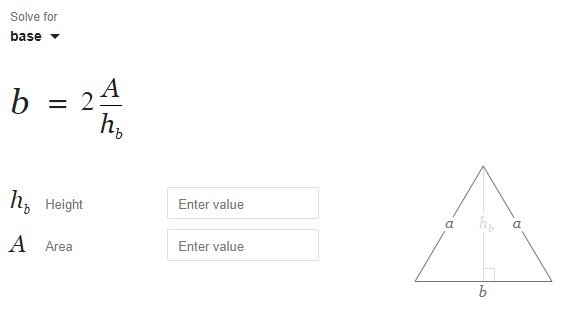
اندازههای بالای خط (base و height در تصویر بالا)، اندازههای مورد استفاده برای محاسبه مساحت هستند. با انتخاب هر یک از گزینههای بالا یا پایین خط، فرمول و کادرهای ورود اعداد در ماشین حساب گوگل، برای محاسبه اندازه مورد نظر تغییر میکنند. به عنوان مثال، اگر بر روی گزینه «base» کلیک کنیم، کادر محاسبات به شکل زیر نمایش داده میشود.
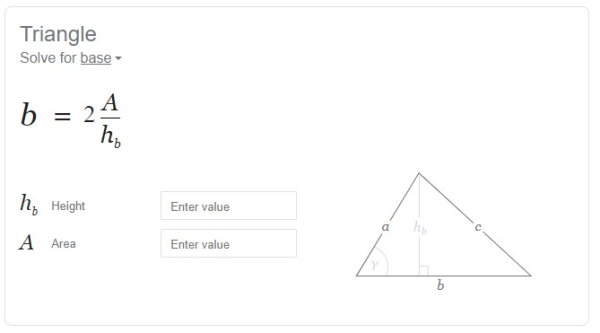
به منظور بررسی عملکرد این ابزار، مساحت و ارتفاع مثال اول مقاله را وارد میکنیم (مساحت 7 سانتیمتر و ارتفاع 4 سانتیمتر).
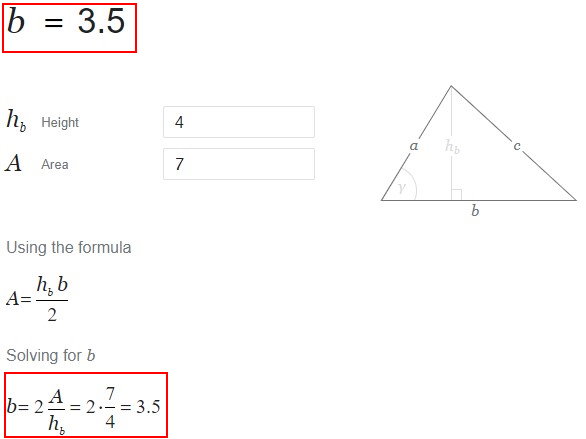
به این ترتیب، اندازه قاعده مثلث و روند محاسبه آن به نمایش در میآید. در صورت نیاز به محاسبه قاعده با سینوس، یکی از گزینههای side (a) یا side (b) را انتخاب کنید. با کلیک بر روی گزینه «perimeter» و انتخاب قاعده مورد نظر، امکان محاسبه قاعده بر اساس محیط فراهم میشود. گوگل، ابزارهای متنوعی برای انجام محاسبات انواع مثلث دارد. با جستجوی عبارتهای زیر، به این ابزارها دسترسی پیدا میکنید:
- isosceles triangle: محاسبه محیط، مساحت، قاعده و ارتفاع مثلثهای متساوی الساقین
- equilateral triangle: محاسبه محیط، مساحت و قاعده مثلثهای متساوی الاضلاع
- right triangle: محاسبه محیط، مساحت، ساق و وتر مثلثهای قائم الزاویه
سوالات متداول قاعده مثلث
در این مطلب از مجله فرادرس در مورد قاعده مثلث و نقش آن در محاسبه مساحت صحبت کردیم. در این بخش، به برخی از سوالات پرتکرار در زمینه قاعده انواع مثلث و نحوه پیدا کردن آنها پاسخ میدهیم.
تعریف قاعده مثلث چیست؟
به ضلع مورد استفاده برای محاسبه مساحت مثلث، قاعده مثلث میگویند. در برخی از موارد، به ضلع پایینی مثلث که یک ارتفاع بر آن عمود شده باشد، قاعده مثلث گفته میشود.
کاربرد قاعده در محاسبات مثلث چیست؟
با قرار دادن اندازه قاعده در فرمول قاعده ضربدر ارتفاع تقسیم بر دو، میتوان مساحت مثلث را به دست آورد.
خواص قاعده های مثلث چه هستند ؟
مجموع اندازه دو قاعده از اندازه قاعده سوم بیشتر است. به علاوه، اندازه قاعده رو به روی بزرگترین زاویه مثلث، بزرگترین اندازه را در میان قاعدههای مثلث دارد.
چگونه قاعده مثلث را پیدا کنیم؟
شما میتوانید قاعده مثلث را با استفاده فرمولهای مساحت مثلث، روابط مثلثاتی (مانند قانون سینوسها)، قضیه فیثاغورس، و فرمولهای محیط پیدا کنید. این مطالب به زبان ساده در مجله فرادرس توضیح داده شدهاند.
قاعده مثلث قائم الزاویه کجاست؟
ساقهای مثلث قائم الزاویه، دو قاعده این نوع مثلث هستند. وتر (ضلع مقابل زاویه 90 درجه)، به عنوان قاعده سوم در نظر گرفته میشود.
قاعده مثلث متساوی الساقین کجاست؟
در مثلثهای متساوی الساقین، ضلع میان زوایای هم اندازه، قاعده مثلث است.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت مثلث — انواع مثلث و تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- مثلث چیست ؟ — به زبان ساده (+ دانلود فیلم آموزش رایگان)
- مساحت انواع مثلث چگونه بدست می آید ؟ — حل تمرین و مثال های متنوع
- محیط مثلث چگونه بدست می آید؟ + فیلم آموزش رایگان
- چگونه مساحت مثلث را حساب کنیم؟ + فیلم آموزشی و تمرین با جواب
- محاسبه آنلاین مساحت مثلث — معرفی بهترین سایتها + مثال
- فرمول محیط مثلث چیست ؟ انواع فرمول ها + حل مثال های متنوع
- فرمول مساحت مثلث چیست ؟ — تمام فرمول ها + حل تمرین
- قاعده مثلث چیست و چگونه بدست می آید ؟ + تعریف و مثال(همین مطلب)
- ارتفاع مثلث چیست و چگونه رسم می شود ؟ — آموزش تصویری + حل تمرین
- محاسبه ارتفاع مثلث — تعریف، حل تمرین و مثال + جدول فرمول ها
- محیط مثلث مختلف الاضلاع — به زبان ساده + حل مثال های متنوع
- چگونه مساحت مثلث مختلف الاضلاع را حساب کنیم؟ + حل تمرین و مثال
- چگونه مساحت مثلث با سه ضلع معلوم را حساب کنیم؟ + حل تمرین و مثال
- فرمول هرون — به زبان ساده
- مساحت مثلث با سینوس چگونه محاسبه می شود ؟ + حل تمرین و جدول فرمول ها
- مثلث قائم الزاویه چیست ؟ — تعریف، ویژگی ها و محاسبات | به زبان ساده
- محیط مثلث قائم الزاویه — به زبان ساده + حل مثال های متنوع
- مساحت مثلث قائم الزاویه — حل تمرین و مثال های متنوع
- مثلث متساوی الساقین چیست ؟ | تعریف، ویژگی ها و محاسبات — به زبان ساده
- محیط مثلث متساوی الساقین — به زبان ساده و با حل مثال
- مساحت مثلث متساوی الساقین — حل تمرین و مثال های متنوع
- محیط مثلث متساوی الاضلاع چگونه بدست می آید؟ + حل مثال و تمرین
- مساحت مثلث متساوی الاضلاع — حل تمرین و مثال های متنوع












