گاز واقعی (حقیقی) — از صفر تا صد

به گازی که انحرافی از حالت ایدهآل داشته باشد، گاز واقعی میگویند. در حقیقت، گاز واقعی رفتاری متفاوت با گاز ایدهآل دارد. در این خصوص باید شرایطی را در نظر بگیریم تا بتوانیم رفتار یک گاز را به هنگام انحراف از حالت ایدهآل بیان کنیم. انحراف گازها از رفتار ایدهآل، از دو عامل ناشی میشود:
- نظریهای که فرض میکند، با افزایش فشار، حجم گاز، بسیار کم میشود و به صفر میرسد. اگرچه حجم گاز مقدار بسیار کمی خواهد شد اما مقدار آن به صفر نخواهد رسید چراکه مولکولها، فضا را اشغال میکنند و فشرده نمیشوند.
- نیروهای بین مولکولی در گازها نیز وجود دارند. این مورد به خصوص در دماهای پایین و به هنگام گاهش حرکات مولکولی، مهم جلوه میکند. البته در دماهای بالا و معمول، نیروهای بین مولکولی بسیار کوچک هستند و میتوان از آنها صرف نظر کرد.
مقدمه
درحالیکه نظریه جنبشی گازها (نظریه سینتیک-مولکولی)، توصیف مناسبی از گازها دارد، اما برخی خواص وجود دارند که این نظریه، خاصه در مورد گاز واقعی نمیتواند آنها را توصیف کند. در این نظریه، فرضیات زیر وجود دارند:
- برخورد بین مولکولهای گاز و دیواره ظرف، به صورت الاستیک رخ میدهد.
- ذرات گاز، حجمی ندارند.
- هیچ نیروی جاذبه و دافعهای بین مولکولها وجود ندارد.
فرضیات بالا در خصوص گازهای ایدهآل کاربرد دارند. با وجود اینکه به طور کلی، فرضیات بالا صحیح هستند اما در برخی موارد، انحرافی از این حالت ایدهآل رخ میدهد. تحت دو حالت مختلف، گازها، رفتاری ایدهآل از خود نشان میدهند:
- گازها در دماهای بالا، رفتار ایدهآل دارند چراکه در دمای زیاد، مولکولها با سرعت بسیار زیادی در حال حرکت هستند.
- در فشار کم نیز، گازها رفتاری ایدهآل دارند، زیرا در فشارهای پایین، حجم مولکولها در مقایسه با حجم کل گاز قابل صرف نظر است. این پدیده را میتوان با قانون بویل توضیح داد که بیان میکند فشار و دما به صورت معکوس با یکدیگر مرتبط هستند.
دو مورد اشاره شده در بالا، شرایط رفتار ایدهآل را بیان میکردند. حال این سوال پیش میآید که چه زمانی گازها رفتاری غیر ایدهآل دارند. گازها در دماهای پایین، رفتاری غیرایدهآل دارند زیرا در دماهای پایین، مولکولهای با سرعت بسیار کمی از کنار یکدیگر عبور میکنند و در اثر این اتفاق، نیروهای جاذبه و دافعه بین مولکولها و انحراف از رفتار ایدهآل رخ میدهد. گازها همچنین در فشارهای زیاد، غیرایدهآل رفتار میکنند چراکه در این حالت، حجم مولکولها قابل صرفنظر کردن نیست.
گاز واقعی و حجم مولی
برای نشان دادن اختلافهای جزئی بین خواص گاز واقعی و ایدهآل در فشار و دمای معمول، مثال زیر را در نظر بگیرید. لازم به ذکر است که برای محاسبه حجم مولی یک گاز ایدهآل در شرایط STP (فشار و دمای استاندارد)، از معادله گازهای ایدهآل استفاده کردهایم.
اگر چگالی یک گاز را در دما و فشار مشخص داشته باشیم، محاسبات حجم مولی بسیار ساده خواهد بود. به طور مثال، در دمای و فشار ۱ اتمسفر، چگالی هلیوم برابر با است. در حقیقت، مقدار هلیوم، در شرایط استاندارد، حجمی برابر با اشغال میکند. با دانستن این اطلاعات، مقدار حجم اشغال شده ۱ مول از مولکول نیز بدست میآید. با توجه به اینکه جرم ۱ مول از هلیوم با عدد اتمی ۴ در جدول تناوبی عناصر، ۴ گرم است، حجم اشغال کننده این گاز به صورت زیر محاسبه میشود:
این مقدار، با عدد ذکر شده برای گاز ایدهآل یکسان است و بیان میکند که هلیوم، در این شرایط، رفتاری همچون گازهای ایدهآل دارد. اگر این کار را برای نمونههای تصادفی از سایر گازها انجام دهید، در محاسبه حجم مولی در شرایط استاندارد، به اعداد مشابهی برمیخورید. جدول زیر، حجم مولی و چگالی را برای برخی گازها نشان میدهد:
| نوع گاز | چگالی | حجم مولی در شرایط استاندارد |
| 0/1785 | 22/4 | |
| 1/2506 | 22/4 | |
| 1/4290 | 22/4 | |
| 0/717 | 22/3 | |
| 1/977 | 22/3 | |
| 1/260 | 22/2 | |
| 0/769 | 22/1 | |
| 2/926 | 21/9 |
در نتیجه، به جهت سادگی در محاسبات، برای تمامی گازها در شرایط استاندارد، حجم را در نظر میگیریم. قابل مشاهده است که این مقادیر، به طور دقیق در همه شرایط، یکسان نیست. حتی در فشارها و دماهای معمول، انحرافی در رفتار گازهای حقیقی نسبت به ایدهآل دیده میشود. این انحراف، تحت شرایط غیر معمول بیشتر خواهد شد که در ادامه به آن خواهیم پرداخت.
ضریب تراکم پذیری
همانطور که میدانید، برای یک گاز ایدهآل، رابطه زیر برقرار است:
برای یک گاز واقعی، دو طرف معادله با یکدیگر مساوی نیستند. به همین منظور، ضریبی با عنوان «ضریب تراکمپذیری» (Compressibility Factor) یا فاکتور Z، طبق رابطه زیر تعریف میشود:
فاکتور Z، معیاری برای اندازهگیری انحراف یک گاز از حالت ایدهآل به شمار میآید. با کمی دقت متوجه میشویم که مقدار ضریب تراکمپذیری برای یک گاز کامل، طبق رابطه زیر، برابر با ۱ است.
در یک گاز واقعی، زمانی که فشار گاز افزایش پیدا کند، مقدار Z، عددی بزرگتر از ۱ خواهد شد که همان انحراف از رفتار ایدهآل را نشان میدهد. این روند را میتوان به هنگام کاهش دما نیز مشاهده کرد چراکه با رسیدن دما به مقداری کم، ضریب تراکمپذیری، بیشتر خواهد شد. همانطور که گفته شد، ضریب تراکمپذیری در گازهای ایدهآل، مقداری برابر با ۱ دارد اما نمودار زیر نشان میدهد که این مقدار با تغییرات زیادی برای یک گاز واقعی همراه است. در این نمودار، تغییرات ضریب تراکمپذیری را به هنگام تغییر فشار و دمای گاز نیتروژن مشاهده میکنید:
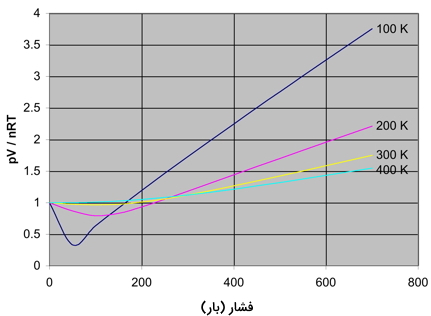
در خصوص نمودار بالا، نکات مهمی را باید در نظر گرفت که در ادامه آورده شده است:
- در فشارهایی کم و در حدود $$1 \bar$$، ضریب تراکمپذیری نزدیک به ۱ است. در چنین فشاری، نیتروژن، رفتاری ایدهآل از خود نشان میدهد.
- رفتار غیر ایدهآل گاز در دماهای پایین، بیشتر است. برای دماهای ۳۰۰-۴۰۰ کلوین، ضریب تراکمپذیری، حتی در فشارهای بالاتر، مقداری برابر با ۱ دارد.
- انحراف از رفتار ایدهآل، در فشارهای بالاتر، بیشتر میشود.
سایر گازها
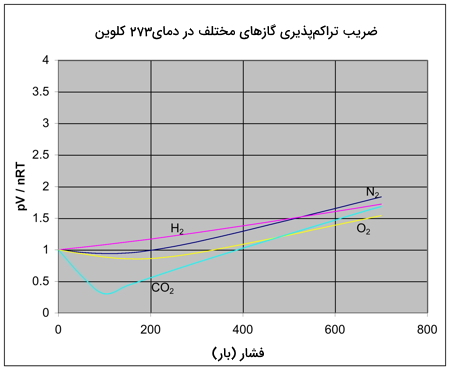
نمودار زیر، تغییرات Z را برای چند گاز دیگر در دمای ثابت نشان میدهد. اگر نموداری همچون نمودار بالا را بخواهیم برای این گازها رسم کنیم، دستهای از نمودارها پدید میآیند که همگی به نمودار نیتروژن شبیه هستند. اما آنچه که در این دسته از نمودارها عوض میشود، دمایی است که در آن، شکل نمودار تغییر میکند. به طور مثال، اگر به نمودار دیاکسید کربن در دمای نگاه کنید، شبیه به نمودار نیتروژن در است.
میتوان گفت که گازها در دماهای پایین، رفتاری غیر ایدهآل دارند اما این دمای پایین، برای هر گاز متفاوت است. با نزدیک شدن به دمای میعان گاز، انحراف از رفتار ایدهآل بیشتر خواهد شد. در حقیقت، هرقدر به این دما در گازی نزدیکتر شویم، تغییرات ضریب تراکمپذیری بیشتر خواهد بود.
علت رفتار غیر ایدهآل
در تعریف رابطه مربوط به Z، طرف راست معادله را میتوان به طور دقیق اندازهگیری کرد. البته این اندازهگیری دقیق را نمیتوان به راحتی برای دما و فشار انجام داد. در فرضیاتی که برای گاز ایدهآل مطرح کردیم، دو مورد ذکر شده بودند که در یک گاز واقعی صحت نداشتند و این دو مورد هر دو بر فشار و دما تاثیرگذار هستند.
مشکل حجم
نظریه جنبشی فرض میکند که در یک گاز ایدهآل، حجم اشغالی مولکولها در مقایسه با حجم ظرف قابل صرفنظر است. برای یک گاز واقعی نمیتوان چنین فرضی را صحیح دانست و مولکولهای گاز، نسبت به ظرف، حجمی را اشغال میکنند. در نتیجه، فضای موجود در ظرف، برای حرکت مولکولها، کمتر از مقدار اندازهگیری شده ظرف خواهد بود. تغییرات این مقدار را میتوان در تصویر زیر مشاهده کرد.
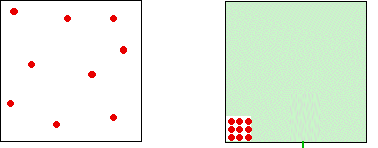
هرقدر گاز، متراکمتر شود، موضوع کاهش حجم بیشتر خود را نشان میدهد. اگر فشار، کم باشد، حجم اشغالی مولکولها در مقایسه با حجم ظرف، مقدار کمی دارد. اما هرقدر که گاز را متراکمتر میکنیم، نسبت حجم اشغالشده توسط مولکولها، بیشتر و بیشتر میشود. میتوان فرض کرد گاز را تا جایی متراکم کنیم که مولکولهای آن در تماس با یکدیگر باشند. در این نقطه، حجم در دسترس برای حرکت مولکولها به صفر میرسد.
فرض کنید که در فشار زیادی، حجم ظرف را اندازهگیری و مقداری برابر با برای آن ذکر کرده باشید. همچنین، فرض کنید که مولکولها، حجمی به اندازه اشغال میکنند. اگر با فرض گازهای ایدهآل، ضریب تراکمپذیری را محاسبه کنید، مقدار حجمی که در محاسبه عبارت دخیل کردهاید، بیشتر از مقدار واقعی است چراکه در حالت واقعی، را باید برای حجم در نظر گرفت.
مشکل فشار
فرض دیگری که در نظریه جنبشی گازها مطرح میشود این است که هیچ نیروی بین مولکولی، بین مولکولهای یک گاز در ظرف وجود ندارد. این فرض نیز برای یک گاز واقعی صحیح نیست. اگر هیچ نیروی بین مولکولی وجود نداشت، آنگاه تبدیل یک گاز به مایع، غیر ممکن بود. حتی هلیوم که کمترین نیروهای بین مولکولی را دارد نیز با کاهش دما، به مایع تبدیل میشود.
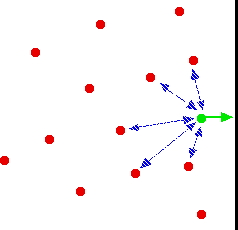
بنابراین، تاثیر نیروهای بین مولکولی چگونه است؟ اگر یک مولکول گاز را در میانه یک ظرف در نظر بگیریم، نیروهای بین مولکولی تاثیری نخواهند داشت چراکه نیروهای جاذبهای که از اطراف و مولکولهای دیگر به آن وارد میشوند، یکدیگر را خنثی میکنند.

میزان این نیروها برای مولکولی که در حال برخورد به دیواره ظرف باشد، متفاوت است. در این حالت، هیچ مولکول دیگری در مسیر آن وجود ندارد. اگر از سرعت آن کاسته شود، با شدت کمتری به دیواره برخورد و در نتیجه، فشار کمتری را به ظرف اعمال میکند. تاثیر کلی این روند را میتوان اینطور بیان کرد که فشار اندازهگیری شده، کمتر از مقدار مورد انتظار برای یک گاز ایدهآل است.
در حقیقت، اگر مقدار اندازهگیری شده فشار را در عبارت قرار دهید، مقدار ضریب تراکمپذیری، کمتر از مقدار آن برای یک گاز ایدهآل خواهد بود. به همین دلیل، تحت شرایطی، نمودار ضریب تراکمپذیری، مقداری کمتر از ۱ دارد و این مورد را میتوان به صورت یک علامت در نمودار مربوطه، مشاهده کرد.
این اثر، اهمیت ویژهای در دماهای پایین دارد زیرا در دماهای پایینتر، سرعت حرکت مولکولها به طور متوسط، آهستهتر است. در دماهای بالاتر، جایی که مولکولها با سرعت بیشتری حرکت میکنند، هر نوع کششی که از مولکولهای اطراف وارد شود، با قدرت کمتری حس خواهد شد. به همین دلیل در دماهای بالا، اثر نیروهای بینمولکولی قابل صرفنظر کردن است.
عامل دیگری هم در خصوص نیروهای بینمولکولی وجود دارد که به خوبی مشخص نیست. با افزایش فشار، مولکولها، بیشتر به یکدیگر فشرده میشوند. زمانی که این مولکولها به یکدیگر نزدیکتر میشوند، نیروهای بینمولکولی اهمیت بیشتری پیدا میکنند. در نتیجه، با افزایش فشار در اثر این تراکم، انتظار داریم که مقدار ضریب تراکمپذیری، نسبت به گاز ایدهآل، کاهش بیشتری پیدا کند. در این خصوص، مولکولهایی که در نزدیکی ظرف قرار دارند، تاثیر بیشتری خواهند داشت.
بهتر است دوباره نگاهی به نمودار نیتروژن در بیاندازیم. همزمان با افزایش فشار، به یکباره مقدار ضریب تراکمپذیری کاهش پیدا میکند اما خیلی زود این مقدار دوباره افزایش مییابد زیرا در این حالت، اهمیت اندازه مولکولها بیشتر خواهد شد و با افزایش بیشتر فشار، سایر اثرات بر فرآیند، حاکم میشوند.
ایدهآلترین گاز
با توجه به فرضیاتی که در خصوص یک گاز ایدهآل مطرح شد، باید گفت که گازی با کوچکترین اندازه مولکولی و کمترین نیروی بین مولکولی را میتوان ایدهآلترین گاز دانست. گاز هلیوم چنین ویژگی دارد. یک مولکول هلیوم شامل یک اتم تنهاست و نیروی واندروالس، در کمترین حالت خود قرار دارند. همانند هلیوم، مولکول هیدروژن (به صورت دواتمی) نیز دو الکترون دارد و نیروهای بین مولکولی در آن، پایین است.
در یک مولکول هیدروژن، دو اتم داریم که میتوان بار الکتریکی را بین آندو توزیع کرد. هر قدر مولکول، بزرگتر شود، نیروهای پراکندگی افزایش مییابند و نیروهای دیگری همچون جاذبه دوقطبی-دوقطبی نیز به آن اضافه میشوند. گازهایی که از چنین مولکولهایی تشکیل شده باشند، انحراف بیشتری از حالت ایدهآل خواهند داشت.
معادلات مختلف برای توصیف رفتار گاز واقعی
در ادامه قصد داریم تا روابط و مدلهای ریاضی مختلفی که برای توصیف رفتار گاز واقعی ارائه شدهاند را بررسی کنیم.
معادله واندروالس
معادلات مختلفی برای توصیف رفتار گاز واقعی ارائه شدهاند که از میان آنها، سادهترین معادله، رابطه واندروالس است و به صورت زیر تعریف میشود:
- : فشار
- : حجم (لیتر)
- : تعداد مول
- : ثابت گازها با مقدار
- : دمای مطلق (کلوین)
با کمی دقت درمییابیم که این معادله، شباهت بسیاری به رابطه دارد. سمت راست معادله، دقیقا با معادله گازهای ایدهآل برابر است. تنها تصحیحاتی که دیده میشود، در خصوص فشار و دما است تا بتوانند نیروهای بین مولکولی و حجم مولکولهای گاز را توصیف کنند.
عبارت ، به فشار اضافه شده است تا تصحیحی برای جاذبه نیروهای بین مولکولی باشد. در این رابطه، ، میزان جاذبه بین هر ذره را توصیف میکند. مقدار کلی نیروهای جاذبه است و به مقدار گاز موجود بستگی دارد. در ادامه، این عبارت را بر تقسیم و به فشار اضافه میکنند چراکه فشار اندازهگیری شده، کمتر از مقدار مورد انتظار است.
عدد ، حجم حذف شده در هر مول به شمار میآید و با حجم مولهای گاز مرتبط است. این مقدار را به این دلیل اضافه میکنند زیرا مولکولهای گاز، حجم دارند. در نتیجه، حجم اندازهگیری شده، شامل حجم مولکولها نیز میشود. برای اینکه رابطه دقیقی بدست بیاید، حجم هر مول را از حجم اندازهگیری شده کم میکنند تا حجم در دسترس گاز بدست آید.
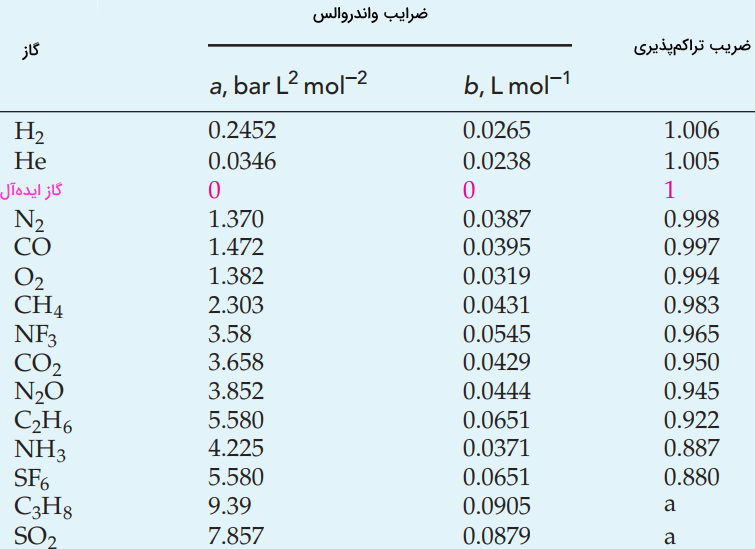
توجه داشته باشید که مقادیر a و b، برای یک گاز، اعداد ثابتی هستند و در اثر دما و فشار، تغییر بسیار کمی دارند. اما این مقدار در هر گاز متفاوت است. جدول زیر، مقادیر ثابتهای معادله واندروالس را به همراه ضریب تراکمپذیری در فشار $$10 \bar$$
مثال
با استفاده از معادله واندروالس، فشار اعمال شده توسط ۱ مول گاز محبوس در محفظهای به حجم ۲ لیتر و دمای را حساب کنید. ثابتهای معادله واندروالس در زیر آورده شدهاند:
$$a=6.34 \text { \bar } \mathrm{L}^{2} \mathrm{mol}^{-2}$$
به نوع تبدیل واحدها در حل این مساله توجه داشته باشید و به هنگام حل، از واحدهای صحیح استفاده کنید.
حل معادله واندروالس برای فشار به صورت زیر خواهد بود:
با جایگذاری مقادیر مورد نظر در معادله خواهیم داشت:
$$\begin{aligned}<br /\> n &\;=1.00 \mathrm{mol} \; V=2.00 \mathrm{L} \; T=273 \mathrm{K} \; R=0.08314 \text { \bar } \mathrm{L} \mathrm{mol}^{-1} \mathrm{K}^{-1} \<br /\> n^{2} a &\;=(1.00)^{2} \mathrm{mol}^{2} \times 6.34 \frac{\mathrm{\bar} \mathrm{L}^{2}}{\mathrm{mol}^{2}}=6.34 \mathrm{\bar} \mathrm{L}^{2} \<br /\> n b &\;=1.00 \mathrm{mol} \times 0.0542 \mathrm{L} \mathrm{mol}^{-1}=0.0542 \mathrm{L} \<br /\> P &\;=\frac{1.00 \mathrm{mol} \times 0.08314 \mathrm{\bar} \mathrm{L} \mathrm{mol}^{-1} \mathrm{K}^{-1} \times 273 \mathrm{K}}{(2.0542) \mathrm{L}}-frac{6.34 \mathrm{\bar} \mathrm{L}^{2}}{(2.00)^{2} \mathrm{L}^{2}} \<br /\> P &\;=11.7 \mathrm{\bar}-1.6 \mathrm{\bar}=10.1 \mathrm{\bar}<br /\> \end{aligned}$$
اگر با استفاده از دادههای بالا و حل آن به کمک معادله گازهای ایدهآل، فشار را محاسبه کنیم، به عدد $$11.3 \bar$$
لازم به ذکر است، مقادیر تجربی و ثابت a و b را میتوان به کمک دمای بحرانی و فشار بحرانی و با استفاده از روابط زیر تخمین زد:
$${\displaystyle {\begin{aligned}a&\;={\frac {27R^{2}T_{\text{c}}^{2}}{64p_{\text{c}}}}\b&\;={\frac {RT_{\text{c}}}{8p_{\text{c}}}}\end{aligned}}}$$
همچنین، با استفاده از روابط مربوط به فشار، حجم و دمای کاهش یافته، معادله را میتوان بر اساس «فشار کاهشیافته» (Reduced Pressure) به صورت زیر نوشت:
معادله ردلیش کوانگ
«معادله ردلیش-کوانگ» (Redlich-Kwong Model)، نوع دیگری از معادلات ۲ پارامتری است که برای مدلسازی گازهای حقیقی بکار میرود. این رابطه، همواره دقیقتر از معادله واندروالس است. در مواردی حتی این معادله، از سایر معادلات با بیش از دو پارامتر نیز دقت بیشتری دارد. رابطه ردلیش-کوانگ را به صورت زیر نشان میدهند:
$${\displaystyle RT=\left(p+{\frac {a}{{\sqrt {T}}V_{\text{m}}\left(V_{\text{m}}+bright)}}\right)\left(V_{\text{m}}-bright)}$$
با حل معادله برای فشار خواهیم داشت:
$${\displaystyle p={\frac {RT}{V_{\text{m}}-b}}-{\frac {a}{{\sqrt {T}}V_{\text{m}}\left(V_{\text{m}}+bright)}}}$$
توجه داشته باشید که مقادیر تجربی a و b در معادله بالا، با مقادیر رابطه واندروالس یکسان نیستند و به کمک روابط زیر میتوان آنها را محاسبه کرد:
$${\displaystyle {\begin{aligned}a&\;=0.42748\,{\frac {R^{2}{T_{\text{c}}}^{\frac {5}{2}}}{p_{\text{c}}}}\b&\;=0.08664\,{\frac {RT_{\text{c}}}{p_{\text{c}}}}\end{aligned}}}$$
شکل کاهش یافته معادله ردلیش-کوانگ را به صورت زیر نشان میدهند:
$${\displaystyle p_{r}={\frac {3T_{r}}{V_{r}-b'}}-{\frac {1}{b'{\sqrt {T_{r}}}V_{r}\left(V_{r}+b'right)}}}$$

معادلات بارتلت
معادله دیگر در شبیهسازی رفتار گاز واقعی، «رابطه بارتلت» (Berthelot Equation) است که به صورت زیر تعریف میشود:
البته مدل «بهبود یافته» (Modified) معادله بارتلت، دقت بیشتری دارد و به شکل زیر است:
معادله دیتریچی
استفاده از «رابطه دیتریچی» (Dieterici Model) در سالهای اخیر کاهش پیدا کرده است. روابط آن به صورت زیر تعریف میشوند:
معادله کلازیوس
این معادله، از جمله سادهترین معادلات ۳ پارامتری محسوب میشود که به کمک آن میتوان رفتار یک گاز واقعی را مدلسازی کرد. رابطه اصلی آن را به صورت زیر نشان میدهند:
$${\displaystyle RT=\left(p+{\frac {a}{T(V_{\text{m}}+c)^{2}}}\right)\left(V_{\text{m}}-bright)}$$
با حل معادله برای فشار خواهیم داشت:
$${\displaystyle {\begin{aligned}a&\;={\frac {27R^{2}T_{\text{c}}^{3}}{64p_{\text{c}}}}\b&\;=V_{\text{c}}-{\frac {RT_{\text{c}}}{4p_{\text{c}}}}\c&\;={\frac {3RT_{\text{c}}}{8p_{\text{c}}}}-V_{\text{c}}\end{aligned}}}$$

معادله ویریال
از «مدل ویریال» (Virial Model) نیز بمنظور توصیف رفتار گاز واقعی بهره میگیریم و رابطه آن به صورت زیر بیان میشود.
در این رابطه، ضرایب A، B، C، ، و ، ثابتهای وابسته به دما هستند.
$${\displaystyle pV_{\text{m}}=RTleft[1+{\frac {B(T)}{V_{\text{m}}}}+{\frac {C(T)}{V_{\text{m}}^{2}}}+{\frac {D(T)}{V_{\text{m}}^{3}}}+ldots \right]}$$
نوع دیگر این رابطه به صورت زیر است:
$${\displaystyle pV_{\text{m}}=RTleft[1+B'(T)p+C'(T)p^{2}+D'(T)p^{3}\ldots \right]}$$
معادله پنگ-رابینسون
معادله حالت پنگ-رابینسون را در مدلسازی گاز واقعی و برخی مایعات نیز میتوان بکار برد:
$${\displaystyle p={\frac {RT}{V_{\text{m}}-b}}-{\frac {a(T)}{V_{\text{m}}\left(V_{\text{m}}+bright)+bleft(V_{\text{m}}-bright)}}}$$
این رابطه را به صورت زیر نیز نشان میدهند:
در رابطه بالا، را «ضریب بیمرکزی» (Acentric Factor) مینامند. همچنین با در نظر گرفتن رابطه ، معادله پنگ-رابینسون را میتوان به صورت یک چندجملهای نوشت:
$${\displaystyle Z^{3}-(1-B)Z^{2}+left(A-2B-3B^{2}\right)Z-left(AB-B^{2}-B^{3}\right)=0}$$
مدلها و روابط دیگری هم برای توصیف رفتار یک گاز واقعی توسعه داده شدهاند اما موارد پرکاربرد آن را در این آموزش بررسی کردیم.
اگر این مطلب برای شما مفید بوده است، آموزشها و مطالب زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس شیمی
- مجموعه آموزشهای مهندسی شیمی
- آموزش ترمودینامیک مهندسی شیمی
- فوگاسیته چیست؟ — به زبان ساده
- تعادل شیمیایی — از صفر تا صد
^^