فرادرس
انتگرال عددی — به زبان ساده (+ دانلود فیلم آموزش رایگان)
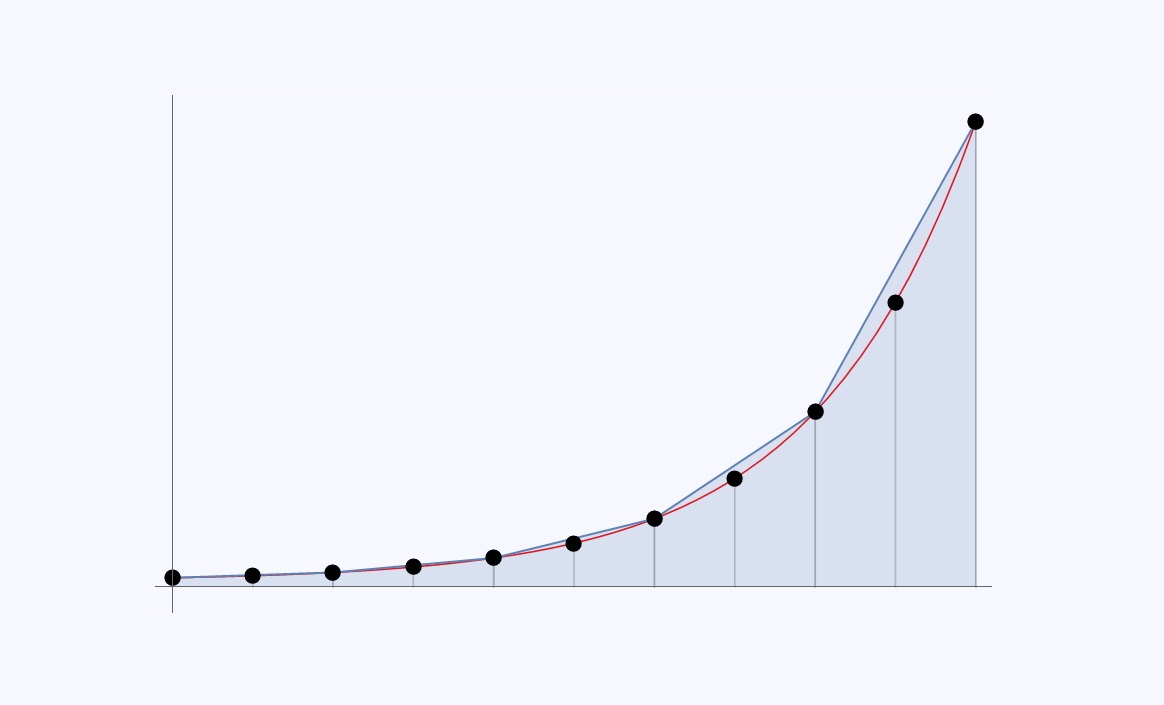
در آموزش‌های پیشین مجله فرادرس با مفهوم انتگرال و روش محاسبه انتگرال برخی از توابع مهم، مانند مثلثاتی، هیپربولیک، نمایی، کسری و گنگ آشنا شدیم. برخی توابع هستند که محاسبه مستقیم پادمشتق و انتگرال آن‌ها دشوار است. در چنین مواردی، اگر بخواهیم مقدار یک انتگرال معین را محاسبه کنیم، باید مقدار آن را تقریب بزنیم و انتگرال عددی را به دست آوریم. دو روش بسیار ساده برای این کار وجود دارد که در ادامه آن‌ها را توضیح می‌دهیم. در برخی موارد نیز ناچار به استفاده از روش‌های پیچیده‌تری هستیم.
اگر انتگرال را به عنوان محاسبه مساحت در نظر بگیریم، می‌توان گفت که با جمع مساحت چندین مستطیل مقدار تقریبی انتگرال به دست می‌آید. هرچند این روش برای محاسبه انتگرال عددی ساده است، اما برای آنکه دقت محاسبه مناسب باشد، به تعداد زیادی مستطیل نیاز داریم. یک راه مشابه و البته بهتر، این است که مساحت زیر منحنی را در یک بازه کوچک با مساحت یک ذوزنقه (روش ذوزنقه‌ای) تقریب بزنیم. شکل زیر نشان می‌دهد که با افزایش تعداد زیربازه‌ها دقت تقریب بیشتر شده است.
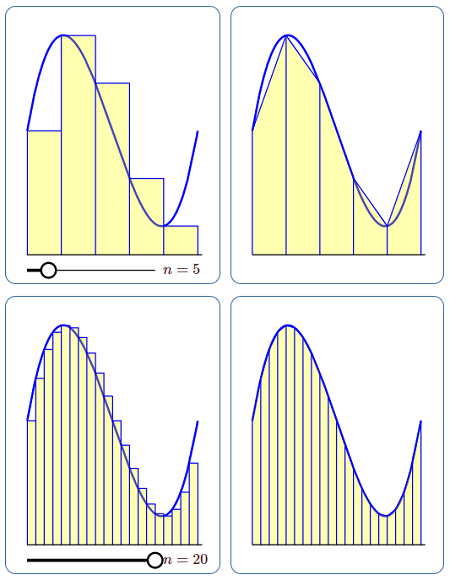
انتگرال عددی با قاعده ذوزنقه‌ای
برای استفاده از این روش، بازه انتگرال‌گیری را به $$n$$ زیربازه به طول $$\Delta x $$ تقسیم می‌کنیم. یک ذوزنقه معمولی در شکل ۲ نشان داده شده که مساحت آن برابر با $$ { f ( x _ i ) + f ( x _ { i + 1 } ) \over 2 } \Delta x $$ است. اگر مساحت کل ذوزنقه‌ها را با یکدیگر جمع کنیم، خواهیم داشت:
$$ \large \eqalign {
{ f ( x _ 0 ) + f ( x _ 1 ) \over 2 } \Delta x & +{ f ( x _ 1 ) + f ( x_ 2 ) \over 2 } \Delta x + \cdots +
{ f ( x _ { n - 1 } ) + f ( x _ n ) \over2 } \Delta x = \cr
& \left ( { f ( x _ 0 ) \over 2 } + f ( x _ 1 ) + f ( x _2 ) + \cdots + f ( x _ { n - 1 } ) + { f ( x _ n ) \over 2 } \right )
\Delta x . \cr } $$
این روش، معمولاً به نام قاعده ذوزنقه‌ای شناخته می‌شود. اگر تعداد زیربازه‌ها خیلی زیاد نباشد، محاسبات با ماشین‌حساب چندان دشوار نخواهد بود. یک کامپیوتر به سادگی برای زیربازه‌های بیشتر قادر به انجام محاسبات است.
در عمل، تقریب انتگرال تنها زمانی مفید است که اندازه دقت را بدانیم. برای مثال، ممکن است به دقتی به اندازه سه رقم اعشار نیاز داشته باشیم. وقتی تقریبی از یک انتگرال را محاسبه می‌کنیم، خطا برابر با اختلاف بین تقریب و مقدار واقعی انتگرال است. از هر روشی که برای انتگرال‌گیری عددی استفاده کنیم، باید یک تخمین خطا (Error Estimate) داشته باشیم. تخمین خطا مقداری است که تضمین شده بزرگ‌تر از خطای واقعی باشد. اگر $$A$$ یک تقریب و $$E$$ تخمین خطای مربوط به آن باشد، آنگاه می‌دانیم که مقدار انتگرال بین $$ A - E $$ و $$ A + E $$ است. در مورد خاص انتگرال‌گیری عددی، می‌خواهیم $$ E = E ( \Delta x ) $$ تابعی برحسب $$ \Delta x $$ باشد که با کوچک شدن $$ \Delta x $$، سریعاً کاهش یابد. خوشبختانه، برای بسیاری از توابع، چنین خطای تخمینی متناظر با تقریب ذوزنقه‌ای وجود دارد.
قضیه: فرض کنید $$ f $$ دارای مشتق دوم $$ f ^ {\prime \prime } $$ در کل بازه $$ [a,b]$$ باشد و برای همه $$x$$ها در این بازه، $$|f^{\prime \prime}(x)|\le M$$. با در نظر گرفتن بازه $$\Delta x= (b-a)/n$$، تخمین خطای تقریب ذوزنقه‌ای به صورت زیر خواهد بود:
$$ \large E ( \Delta x ) = { b - a \over 1 2 } M ( \Delta x ) ^ 2 = { ( b - a ) ^ 3 \over 1 2 n ^ 2 } M . $$
اما چگونه از این قضیه استفاده می‌کنیم؟ مثال زیر پاسخ این پرسش است.
مثال ۱
مقدار انتگرال عددی $$ \int _ 0 ^ 1 e ^ { - x ^ 2 } \, d x $$ را تا دو رقم اعشار بنویسید.
حل: مشتق دوم تابع $$ f=e^{-x^2}$$ برابر با $$ ( 4 x ^ 2 - 2 ) e ^ { - x ^ 2 } $$ است و در بازه $$[0,1]$$، نامساوی $$ | ( 4 x ^ 2 - 2 ) e ^ { - x ^ 2 } | \le 2 $$ را خواهیم داشت. با تخمین تعداد زیربازه‌هایی شروع می‌کنیم که به آن‌ها نیاز داریم. برای داشتن دو رقم اعشار، باید $$E(\Delta x)< 0.005$$ یا
$$ \large \eqalign {
{ 1 \over 1 2 } ( 2 ) { 1 \over n ^ 2 } & < 0 . 0 0 5 \cr
{ 1 \over 6 } ( 2 0 0) & < n ^ 2 \cr
5 . 7 7 \approx \sqrt { 1 0 0 \over 3 } & < n \cr } $$
با $$ n = 6 $$، تخمین خطا $$1/6^3< 0.0047$$ است. اکنون تقریب ذوزنقه‌ای را برای شش زیربازه می‌نویسیم:
$$\large \left ( { f ( 0 ) \over 2 } + f ( 1 / 6 ) + f ( 2 / 6 ) + \cdots + f ( 5 / 6 ) + { f ( 1 ) \over 2 } \right ) { 1 \over 6 }
\approx 0 . 7 4 5 1 2 . $$
بنابراین، مقدار واقعی انتگرال بین $$ 0.74512-0.0047=0.74042$$ و $$ 0.74512+0.0047=0.74982 $$ است. متأسفانه گرد شده مقدار اول $$0.74$$ و گرد شده مقدار دوم $$0.75$$ است. بنابراین، نمی‌توانیم از مقدار صحیح تنها با دو رقم اعشار مطمئن باشیم. در نتیجه، باید یک $$n$$ بزرگ‌تر انتخاب کنیم. همان‌طور که معلوم است، باید $$n=12$$ باشد تا دو محدوده مشابه برای اعشار مورد نظر داشته باشیم. این مقدار $$0.75$$ خواهد بود.
در عمل، معمولاً از مقادیر بهتری برای حداکثر خطای ممکن استفاده می‌شود؛ برای مثال، $$ E ( \Delta x ) < 0 . 0 0 1 $$ انتخاب رایجی است. در این صورت، خواهیم داشت:
$$ \large \eqalign {
{ 1 \over 1 2 } ( 2 ) { 1 \over n ^ 2 } & < 0 . 0 0 1 \cr
{ 1 \over 6 } ( 1 0 0 0 ) & < n ^ 2 \cr
1 2 . 9 1 \approx \sqrt { 5 0 0 \over 3 } & < n \cr } $$
با $$n = 13$$ به نتیجه مطلوب می‌رسیم.
انتگرال عددی با قاعده سیمپسون
تقریب ذوزنقه‌ای عملکرد مناسبی دارد، به ویژه در مقایسه با مستطیل‌ها؛ زیرا وقتی $$ \Delta x $$ به اندازه کافی کوچک باشد، قسمت فوقانی تقریب بهتری از منحنی را ارائه می‌کند. می‌توانیم این ایده را تعمیم دهیم: اگر بخواهیم تقریبمان دقیق‌تر باشد و به جای یک خط راست از چیز دیگری استفاده کنیم، چه اتفاقی می‌افتد؟ یک گزینه بدیهی برای این کار سهمی است. اگر بتوانیم تکه‌های منحنی را با یک سهمی با معادله $$ y=ax^2+bx+c $$ تقریب بزنیم، می‌توانیم به سادگی سطح زیر نمودار را محاسبه کنیم.
برای دو نقطه، تعداد سهمی‌هایی که می‌توان تعریف کرد، بینهایت است؛ اما اگر سه نقطه داشته باشیم، تنها یک سهمی وجود دارد که در آن‌ها صدق می‌کند. اگر بخواهیم یک سهمی را پیدا کنیم که از سه نقطه $$ (x_i,f(x_i)) $$، $$(x_{i+1},f(x_{i+1}))$$ و $$ (x_{i+2},f(x_{i+2})) $$ روی منحنی می‌گذرند، در کل بازه $$[x_i,x_{i+2}]$$ بسیار نزدیک به منحنی است. شکل ۳ این موضوع را به خوبی نشان می‌دهد.
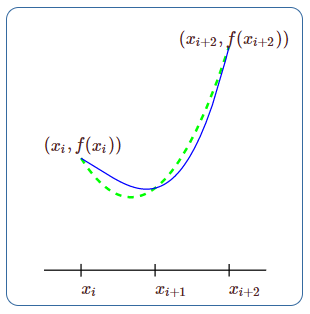
اگر بازه $$ [a , b ] $$ را به تعدادی زیربازه زوج تقسیم کنیم، آنگاه می‌توانیم منحنی را با دنباله‌ای از سهمی‌ها تقریب بزنیم که هر کدام دو زیربازه را پوشش می‌دهند. برای اینکه این کار عملی باشد، به فرمول ساده‌ای برای مساحت زیر یک سهمی گذرنده از $$ (x_i,f(x_i))$$، $$(x_{i+1},f(x_{i+1}))$$ و $$(x_{i+2},f(x_{i+2}))$$ نیاز داریم. یعنی باید سهمی را به صورت $$ y=ax^2+bx+c$$ بنویسیم که از این نقاط عبور کند و سپس از آن انتگرال بگیریم. اگرچه جبر مربوط به این کار پیچیده به نظر می‌رسد، اما انجام آن امکان‌پذیر است.
برای یافتن سهمی، سه معادله زیر را برای $$a$$، $$b$$ و $$ c $$ حل می‌کنیم:
$$ \large \eqalign {
f ( x _ i ) & = a ( x _ { i + 1 } - \Delta x ) ^ 2 + b ( x _ { i + 1 } - \Delta x ) + c \cr
f ( x _ { i + 1 } ) & = a ( x _ { i + 1 } ) ^ 2 + b ( x _ { i + 1 } ) + c \cr
f ( x _ { i + 2 } ) & = a ( x _ { i + 1 } + \Delta x ) ^ 2 + b ( x _{ i + 1 } + \Delta x ) + c \cr } $$
پیچیده بودن حل این معادلات غیرمنتظره نیست. با وجود این، می‌توان انتگرال عددی را محاسبه و ساده کرد:
$$ \large \int _ { x _ { i + 1 } - \Delta x } ^ { x _ { i + 1 } + \Delta x } a x ^ 2 + b x + c \, d x =
{ \Delta x \over 3 } ( f ( x _ i ) + 4 f ( x _ { i + 1 } ) + f ( x _ { i + 2 } ) ) . $$
مجموع سطح زیر همه سهمی‌ها برابر است با:
$$ \large \displaylines {
{ \Delta x \over 3 } (f ( x _ 0 ) + 4 f ( x _ { 1 } ) + f ( x _ { 2 } ) + f ( x _ 2 ) + 4 f ( x _ { 3 } ) + f ( x _ { 4 } ) + \cdots
+ f ( x _ { n - 2 } ) + 4 f ( x _ { n - 1 } ) + f ( x _ { n } ) ) = \cr
{ \Delta x \over 3 } ( f ( x _ 0 ) + 4 f ( x _ { 1 }) + 2 f ( x _ { 2 } ) + 4 f ( x _ { 3 } ) + 2 f ( x _ { 4 } ) + \cdots
+ 2 f ( x _ { n - 2 } ) + 4 f ( x _ { n -1 } ) + f ( x _ {n } ) ) . \cr } $$
این فرمول، تنها کمی پیچیده‌تر از فرمول ذوزنقه‌ها است. باید به خاطر داشته باشیم که ضرایب $$2$$ و $$4$$ را قرار دهیم. عدد $$n$$ نیز باید زوج باشد تا معنی داشته باشد. به این تکنیکِ تقریب، قاعده سیمپسون می‌گویند.
مشابه قاعده ذوزنقه‌ای، یک تخمین خطا برای قاعده سیمپسون نیز وجود دارد.
قضیه: فرض کنید $$f$$ دارای مشتق چهارم $$ f ^ {(4)}$$ در کل بازه $$[a,b]$$ بوده و برای همه $$x$$های این بازه، $$|f^{(4)}(x)|\le M$$. اگر $$\Delta x= (b-a)/n$$، یک تخمین خطا برای تقریب سیمپسون به صورت زیر خواهد بود:
$$ \large E ( \Delta x ) = { b - a \over 1 8 0 } M ( \Delta x ) ^ 4 ={ ( b - a ) ^ 5 \over 1 8 0 n ^ 4 } M . $$
مثال زیر، کاربرد این قضیه را نشان می‌دهد.
مثال ۲
انتگرال عددی $$ \int_0^1 e^{-x^2}\,dx $$ را تا دو رقم اعشار تقریب بزنید.
حل: مشتق چهارم $$ f=e^{-x^2}$$ برابر با $$(16x^2-48x^2+12)e^{-x^2}$$ بوده و روی بازه $$ [0,1]$$ حداکثر مقدار مطلق آن برابر با $$12$$ است. با تخمین تعداد زیربازه‌هایی که نیاز داریم شروع می‌کنیم. برای داشتن دقت دو رقم اعشار، باید $$ E(\Delta x)< 0.005 $$ را داشته باشیم. اما به توجه به مثال قبل، لازم است $$ E(\Delta x)< 0.001 $$ را داشته باشیم:
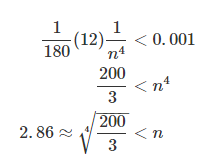
بنابرین، $$ n = 4 $$ را امتحان می‌کنیم، زیرا به تعداد زوجی زیربازه نیاز داریم. سپس تخمین خطا $$ 12/180/4^4< 0.0003 $$ خواهد بود و تقریب برابر است با:
$$ \large ( f ( 0 ) + 4 f ( 1 / 4 ) + 2 f ( 1 / 2) + 4 f ( 3 / 4 ) + f (1 ) ) { 1 \over 3 \cdot 4 }
\approx 0 . 7 4 6 8 5 5 . $$
بنابراین، مقدار واقعی انتگرال بین $$ 0.746855-0.0003=0.746555 $$ و $$ 0.746855+0.0003=0.7471555 $$ خواهد بود که هر دوی آن‌ها به $$ 0.75$$ گرد می‌شوند.
انتگرال عددی با قاعده سیمپسون در متلب
برنامه متلب قاعده سیمپسون نیز به صورت زیر است:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Simpson Rule (Version 1.0) %
% %
% Programmed By: MatlabSite.com Team. %
% Copyright 2009 %
% %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
! Copyright.pdf
clc;
clear;
x=sym('x');
disp('This program calculates integral of f(x) using Composite Simpson rule.');
f=input('Enter f(x) as a function of x: ');
disp(' ');
a=input('Enter the start of integration range: ');
b=input('Enter the end of integration range: ');
disp(' ');
xmin=min(a,b);
xmax=max(a,b);
a=xmin;
b=xmax;
n=input('Enter the number of subintervals (an even number): ');
disp(' ');
n=2*floor(n/2);
if(n<2)
n=2;
end
h=(b-a)/n;
S=0;
for i=1:n+1
xx=a+(i-1)*h;
ff=subs(f,xx);
if i==1 || i==n+1
S=S+ff;
else
if mod(i,2)==0
S=S+4*ff;
else
S=S+2*ff;
end
end
end
S=S*h/3;
disp(['Integral of ' char(f) ' in the range [' mat2str(a,4) ', ' mat2str(b,4) '] is:']);
disp(mat2str(S,10));
disp(' ');
انتگرال عددی با قاعده ذوزنقه‌ای در متلب
برنامه متلب قاعده ذوزنقه‌ای نیز به صورت زیر است:
function I = trapezoidal_f1 ( f )
% for calculating integrals using trapezoidal rule when function is known
%asking for the range and desired accuracy
R= input( ' Enter the limits of integrations [ x_min, x_max] :\n');
tol = input(' Error allowed in the final answer should be of an order : \n');
a= R(1,1); b = R(1,2);
%initial h and n
n = 100;
h = (b -a )/100;
%for calculating maximum of h^2 *f''(x) in the given region
for k = 0:100
x( 1, k+1 ) = a + k*h ;
y2 ( 1, k+1) = feval ( f, x(1,k+1) + 2*h ) - 2*feval( f, x(1,k+1) + h ) + feval( f, x(k+1) );
end
[ y i ] = max( y2);
x_opt = x(1,i);
% for calculating the desired value of h
m=0;
while abs((feval ( f, x_opt + 2*h ) - 2*feval(f, x_opt+ h) + feval(f, x_opt)) * ( b-a)/12) > tol % Global error for trapezoidal rule
m = m +1;
h = h * 10^-m;
end
%calculating n
n = ceil( (b-a)/h );
h = ( b-a )/ n;
% forming matrix X
for k = 1:(n+1)
X(k,1) = a + (k-1)*h;
X(k,2) = feval( f, X(k,1));
end
% trapezoidal formula
I = h/2 * (2*sum( X(:,2))- X(1,2)- X( n,2));
% displaying final result
h
n
disp(sprintf(' The area under this curve in the interval ( %10f , %10f ) is %10.6f .',a,b,I))
اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزش‌های دروس ریاضیات
- آموزش محاسبات عددی با MATLAB
- مجموعه آموزش‌های محاسبات عددی
- آموزش ریاضی پایه دانشگاهی
- روش نیوتن — به زبان ساده
- دستگاه معادلات خطی — به زبان ساده
- جذر یا محاسبه ریشه دوم عدد — به زبان ساده
^^
فیلم های آموزش انتگرال عددی — به زبان ساده (+ دانلود فیلم آموزش رایگان)
فیلم آموزشی انتگرال عددی با قاعده ذوزنقه‌ای
فیلم آموزشی حل مثال از انتگرال عددی با قاعده ذوزنقه‌ای
فیلم آموزشی انتگرال عددی با قاعده سیمپسون
فیلم آموزشی حل مثال از انتگرال عددی با قاعده سیمپسون
فیلم آموزشی خطا در انتگرال عددی
فیلم آموزشی پیاده‌سازی قاعده ذوزنقه‌ای در متلب
فیلم آموزشی کدنویسی الگوریتم سیمپسون در نرم افزار متلب
