انتگرال معین و محاسبه آن — از صفر تا صد
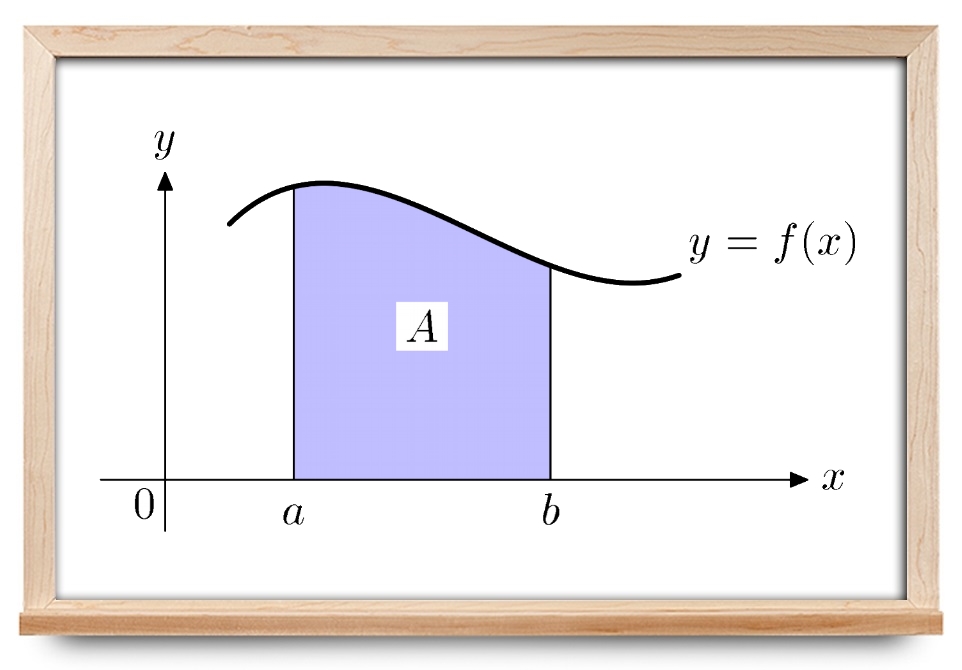
در آموزشهای قبلی مجله فرادرس، روشهای مختلف انتگرالگیری نامعین را معرفی کردیم. همچنین با روشهای عددی انتگرالگیری مانند قاعده سیمپپسون و قاعده ذوزنقهای آشنا شدیم. از انتگرالگیری میتوان برای محاسبه مساحتها، نقاط مرکزی و بسیاری کاربردهای دیگر استفاده کرد. در این آموزش، «انتگرال معین» (Definite Integral) را معرفی و بسیاری از ویژگیهای آن را بیان میکنیم.
تعریف
فرض کنید تابع $$ f\left( x \right) $$ را که در بازه $$ \left[ {a,b} \right] $$ پیوسته است، به $$n$$ زیربازه مساوی به عرض $$ \Delta x $$ تقسیم کرده و از هر زیربازه، نقطه $$ x_i^* $$ را انتخاب میکنیم. آنگاه انتگرال معین تابع $$ f ( x ) $$ از $$a $$ تا $$ b $$ برابر است با:
$$ \large \int _ { { \, a } } ^ { { \, b } } { { f \left ( x \right ) \, d x } } = \mathop { \lim } \limits _ { n \to \infty } \sum \limits _ { i = 1 } ^ n { f \left ( { x _ i ^ * } \right ) \Delta x } $$
عدد پایین نماد انتگرال، یعنی $$a $$، حد پایین و $$b$$ حد بالای انتگرال نامیده میشود. همچنین هیچ اجباری وجود ندارد که $$a $$ کوچکتر از $$b$$ باشد. $$a $$ و $$b $$ بازه انتگرالگیری نامیده میشوند.
در اینجا مثالی با استفاده از سریها مقدار یک انتگرال معین را حساب میکنیم.
مثال ۱
با استفاده از تعریف انتگرال معین، مقدار انتگرال زیر را حساب کنید:
$$ \large \int _ { { \, 0 } } ^ { { \, 2 } } { { { x ^2 } + 1 \, d x } } $$
حل: برای آنکه از تعریف بالا استفاده کنیم، ابتدا باید برای هر بازه، نقاط $$ x_i^* $$ را تعیین کنیم. برای سادگی، نقاط انتهایی هر بازه را در نظر میگیریم. اگر تعداد زیربازهها را $$n$$ فرض کنیم، اندازه هر زیربازه برابر است با:
$$ \large \Delta x = \frac { { 2 - 0 } } { n } = \frac { 2 } { n } $$
در نتیجه، زیربازهها به صورت زیر هستند:
$$ \large \left [ { 0 , \frac { 2 } { n } } \right ] \, , \, \, \, \left [ { \frac { 2 } { n } , \frac { 4 } { n } } \right ] , \, \, \, \left [ { \frac { 4 } { n } , \frac { 6 } { n } } \right ] , \, \, \ldots \, \, , \, \, \left [ { \frac { { 2 \left ( { i - 1 } \right ) } } { n } , \frac { { 2 i } } { n } } \right ] , \, \, \ldots \, \, , \, \, \left [ { \frac { { 2 \left ( { n - 1 } \right ) } } { n } , 2 } \right ] $$
همانطور که میبینیم، نقطه انتهایی زیربازه $$i$$اُم برابر است با:
$$ \large x _ i ^ * = \frac { { 2 i } } { n } $$
در نتیجه، سری موجود در تعریف انتگرال معین، به صورت زیر خواهد بود:
$$ \large \begin {align*} \sum \limits _ { i = 1 } ^ n { f \left ( { x _ i ^ * } \right ) \Delta x } & = \sum \limits _ { i = 1 } ^ n { f \left ( { \frac { { 2 i } } { n } } \right ) \left ( { \frac { 2 } { n } } \right ) } \\ & = \sum \limits _ { i = 1 } ^ n { \left ( { { { \left ( { \frac { { 2 i } } { n } } \right ) } ^ 2 } + 1 } \right ) \left ( { \frac { 2 } { n } } \right ) } \\ & = \sum \limits _ { i = 1 } ^ n { \left ( { \frac { { 8 { i ^ 2 } } } { { { n ^ 3 } } } + \frac { 2 } { n } } \right ) } \end {align*} $$
اکنون باید حد عبارت بالا را محاسبه کنیم. به عبارت دیگر، باید از فرمولهای مربوط به سریها کمک گرفته و فرمولی را برحسب $$n$$ برای حد سری ارائه دهیم.
برای این کار، سری را به صورت زیر مینویسیم:
$$ \large \begin {align*} \sum \limits _ { i = 1 } ^ n { f \left ( { x _ i ^ * } \right ) \Delta x } & = \sum \limits _ { i = 1 } ^ n { \frac { { 8 { i ^ 2 } } } { { { n ^ 3 } } } } + \sum \limits _ { i = 1 } ^ n { \frac { 2 } { n } } \\ & = \frac { 8 } { { { n ^ 3} } } \sum \limits _ { i = 1 } ^ n { { i ^ 2 } } + \frac { 1 } { n } \sum \limits _ { i = 1 } ^ n 2 \\ & = \frac { 8 }{ { { n ^ 3 } } } \left ( { \frac { { n \left ( { n + 1 } \right ) \left ( { 2 n + 1 } \right ) } } { 6 } } \right ) + \frac { 1 } { n }\left ( { 2 n } \right ) \\ & = \frac { { 4 \left ( { n + 1 } \right ) \left ( { 2 n + 1 } \right ) } } { { 3 { n ^ 2 } } } + 2 \\ & = \frac { { 1 4 { n ^ 2 } + 1 2 n + 4 } } { { 3 { n ^ 2 } } } \end {align*} $$
اکنون میتوانیم انتگرال معین را حساب کنیم:
$$ \large \begin {align*} \int _ { { \, 0 } } ^ { { \, 2 } } { { { x ^ 2 } + 1 \, d x } } & = \mathop { \lim } \limits _ { n \to \infty } \sum \limits _ { i = 1 } ^ n { f \left ( { x _ i ^ * } \right ) \Delta x } \\ & = \mathop { \lim } \limits _ { n \to \infty } \frac { { 1 4{ n ^ 2 } + 1 2 n + 4 } } { { 3 { n ^ 2 } } } \\ & = \frac { { 1 4 } } { 3 } \end {align*} $$
برای محاسبه حد سری فوق، روشهای زیادی وجود دارد؛ برای مثال میتوانید آموزش حد در بینهایت را ببینید.
همانطور که دیدیم، اگر از تعریف انتگرال معین استفاده کنیم، یافتن انتگرال معین یک تابع ساده هم به محاسبات زیادی نیاز دارد. راه سادهتری برای محاسبه انتگرال معین وجود دارد که در ادامه آن را معرفی میکنیم. هدف اصلی این بخش، ارائه خصوصیات اصلی انتگرال معین و استفاده از آنها برای محاسبه حاصل انتگرال است.
ابتدا برخی ویژگیهای انتگرال معین را بیان میکنیم.
ویژگیهای انتگرال معین
۱. میتوانیم حدود هر انتگرال معینی را تعویض کرده و در ازای آن، علامت انتگرال را تغییر دهیم:
$$ \large \displaystyle \int _ { { \, a } } ^{ { \, b } } { { f \left ( x \right ) \, d x } } = - \int _ { { \, b } } ^ { { \, a } } { { f \left ( x \right ) \, d x } } $$
۲. اگر حدود بالا و پایین انتگرال برابر باشند، حاصل انتگرال صفر خواهد بود:
$$ \large \displaystyle \int _ { { \, a } } ^ { { \, a } } { { f \left ( x \right ) \, d x } } = 0 $$
۳. مشابه حد، مشتق و انتگرال نامعین، میتوان از یک عدد ثابت فاکتور گرفت:
$$ \large \displaystyle \int _ { { \, a } } ^ { { \, b } } { { c f \left ( x \right ) \, d x } } = c \int _ { { \, a } } ^ { { \, b } } { { f \left ( x \right ) \, d x } } $$
که در آن، $$c $$ یک عدد ثابت دلخواه است.
۴. میتوان انتگرال معین را به دو انتگرال معین دیگر شکست:
$$ \large \displaystyle \int _ { { \, a } } ^ { { \, b } } { { f \left ( x \right ) \pm g \left ( x \right) \, d x } } = \int _ { { \, a } } ^ { { \, b } } { { f \left ( x \right ) \, d x } } \pm \int _{ { \, a } } ^ { { \, b } } { { g \left ( x \right ) \, d x } } $$
۵. بازه انتگرلگیری را میتوان به دو زیربازه متصل به هم $$ \left[ {a,c} \right] $$ و $$ \left[ {c,b} \right] $$ شکست (لزومی ندارد $$c$$ حتماً بین $$a $$ و $$b $$ باشد):
$$ \large \displaystyle \int _ { { \, a } } ^ { { \, b } } { { f \left ( x \right ) \, d x } } = \int _ { { \, a } } ^ { { \, c } } { { f \left ( x \right ) \, d x } } + \int _ { { \, c } } ^ { { \, b } } { { f \left ( x \right ) \, d x } } $$
۶. متغیر انتگرالگیری را میتوان تغییر داد:
$$ \large \displaystyle \int _ { { \, a } } ^ { { \, b } } { { f \left ( x \right ) \, d x } } = \int _ { { \, a } } ^ { { \, b } } { { f \left ( t \right ) \, d t } } $$
۷. برای هر عدد $$c$$، داریم:
$$ \large \displaystyle \int _ { { \, a } } ^ { { \, b } } { { c \, d x } } = c \left ( { b - a } \right ) $$
۸. اگر برای $$ a \le x \le b $$، داشته باشیم: $$ f\left( x \right) \ge 0 $$، آنگاه:
$$ \large \displaystyle \int _ { { \, a } } ^ { { \, b } } { { f \left ( x \right ) \, d x } } \ge 0 $$
۹. اگر برای $$ a \le x \le b $$، داشته باشیم: $$ f\left( x \right) \ge g\left( x \right) $$، آنگاه:
$$ \large \displaystyle \int _ { { \, a } } ^ { { \, b } } { { f \left ( x \right ) \, d x } } \ge \int _ { { \, a } } ^ { { \, b } } { { g \left ( x \right ) \, d x } } $$
۱۰. اگر برای $$ a \le x \le b $$، داشته باشیم: $$ m \le f\left( x \right) \le M $$، آنگاه:
$$ \large m \left ( { b - a } \right ) \le \int _ { { \, a } } ^ { { \, b } } { { f \left ( x \right ) \, d x } } \le M \left ( { b - a } \right ) $$
۱۱. نامعادله زیر برای انتگرال معین برقرار است:
$$ \large \left | { \int _ { { \, a } } ^ { { \, b } } { { f \left ( x \right ) \, d x } } } \right | \le \int _ { { \, a } } ^ { { \, b } } { { \left | { f \left ( x \right ) \, } \right | d x } } $$
در ادامه چند مثال مربوط به این ویژگیها را بیان میکنیم.
مثال ۲
از تساوی زیر (نتیجه مثال قبل) برای محاسبه انتگرالهای زیر استفاده کنید:
$$ \large \int _ { { \, 0 } } ^ { { \, 2 } } { { { x ^ 2 } + 1 \, d x } } = \frac { { 1 4 } } { 3 } $$
(الف) $$ \large \displaystyle \int _ { { \, 2 } } ^ { { \, 0 } } {{ { x ^ 2 } + 1 \, d x } } $$
در این مثال، برای رسیدن به انتگرال مورد نظر، از ویژگی اول استفاده کرده و حدود انتگرال را جابهجا میکنیم. بنابراین، داریم:
$$ \large \begin {align*} \int _ { { \, 2 } } ^ { { \, 0 } } { { { x ^ 2 } + 1 \, d x } } & = - \int _ { { \, 0 } } ^ { { \, 2 } } { { { x ^ 2 } + 1 \, d x } } \\ & = - \frac { { 1 4 } } { 3 } \end {align*} $$
(ب) $$ \large \displaystyle \int _ { { \, 0 } } ^ { { \, 2 } } { { 1 0 { x ^ 2 } + 10 \, d x } } $$
برای حل این انتگرال، از عدد $$ 10 $$ فاکتور میگیریم:
$$ \large \begin {align*} \int _ { { \, 0 } } ^ { { \, 2 } } { { 1 0 { x ^ 2 } + 1 0 \, d x } } & = \int _ { { \, 0 } } ^ { { \, 2 } } { { 1 0 \left ( { { x ^ 2} + 1 } \right ) \, d x } } \\ & = 1 0 \int _ { { \, 0 } } ^ { { \, 2 } } { { { x ^ 2 } + 1 \, d x } } \\ & = 1 0 \left ( { \frac { { 1 4 } } { 3 } } \right ) \\ & = \frac { { 1 4 0 } } { 3 } \end {align*} $$
(ج) $$ \large \displaystyle \int _ { { \, 0 } } ^ { { \, 2 } } { { { t ^ 2 } + 1 \, d t } } $$
در این حالت، تنها متغیر انتگرالگیری تغییر کرده است؛ بنابراین، داریم:
$$ \large \int _ { { \, 0 } } ^ { { \, 2 } } { { { t ^ 2 } + 1 \, d t } } = \int _ { { \, 0 } } ^ { { \, 2 } } { { { x ^ 2 } + 1 \, d x } } = \frac { { 1 4 } } { 3 } $$
مثال ۳
حاصل انتگرال معین زیر را به دست آورید:
$$ \large \int _ { { 1 3 0 } } ^ { { \, 1 3 0 } } { { \frac { { { x ^ 3 } - x \sin \left ( x \right ) + \cos \left ( x \right ) } } { { { x ^ 2 } + 1 } } \, d x } } $$
حل: اگر به بازه انتگرالگیری این انتگرال توجه کنیم، میبینیم که نیازی به محاسبه آن نیست؛ زیرا حد بالا و پایین آن با هم برابر هستند و با توجه به ویژگی دوم، مقدار آن صفر خواهد بود:
$$ \large \int _ { { 1 3 0 } } ^ { { \, 1 3 0 } } { { \frac { { { x ^ 3 } - x \sin \left ( x \right ) + \cos \left ( x \right ) } } { {{ x ^ 2 } + 1 } } \, d x } } = 0 $$
مثال ۴
با فرض $$ \displaystyle \int _ { { \, 6 } } ^ { { \, - 1 0 } } { { f \left ( x \right ) \, d x } } = 2 3 $$ و $$ \displaystyle \int _ { { \, - 1 0 } } ^ { { \, 6 } } { { g \left ( x \right ) \, d x } } = - 9 $$، مقدار انتگرال زیر را به دست آورید:
$$ \large \int _ { { \, - 1 0 } } ^ { { \, 6 } } { { 2 f \left ( x \right ) \, - 1 0 g \left ( x \right ) d x } } $$
حل: در اینجا، باید با استفاده از ویژگی چهارم، انتگرال را به دو انتگرال بشکنیم و از ویژگی سوم استفاده کرده و از اعداد ثابت فاکتور بگیریم:
$$ \large \begin {align*} \int _ { { \, - 1 0 } } ^ { { \, 6 } } { { 2 f \left ( x \right ) \, - 1 0 g \left ( x \right ) d x } } & = \int _ { { \, - 1 0 } } ^ { { \, 6 } } { { 2 f \left ( x \right ) \, d x } } - \int _ { { \, - 1 0 } } ^ { { \, 6 } } { { 1 0 g \left ( x \right ) d x } } \\ & = 2 \int _ { { \, - 1 0 } } ^ { { \, 6 } } { { f \left ( x \right ) \, d x } } - 1 0 \int _ { { \, - 1 0 } } ^ { { \, 6 } } { { g \left ( x \right ) d x } } \end {align*} $$
اکنون از ویژگی نخست کمک میگیریم و حدود انتگرال با هم تعویض میکنیم. بنابراین، داریم:
$$ \large \begin {align*} \int _ { { \, - 1 0 } } ^ { { \, 6 } } { { 2 f \left ( x \right ) \, - 1 0 g \left ( x \right ) d x } } & = - 2 \int _ { { \, 6 } } ^ { { \, - 1 0 } } { { f \left ( x \right ) \, d x } } - 1 0 \int _ { { \, - 1 0 } } ^ {{ \, 6 } } { { g \left ( x \right ) d x } } \\ & = - 2 \left ( { 2 3 } \right ) - 1 0 \left ( { - 9 } \right )\\ & = 4 4 \end {align*} $$
مثال ۵
با استفاده از انتگرالهای $$ \displaystyle \int _ { { \, 1 2 } } ^ { { \, - 1 0 } } { { f \left ( x \right ) \, d x } } = 6 $$ و $$ \displaystyle \int _ { { \, 1 0 0 } } ^ { { \, - 1 0 } } { { f \left ( x \right ) \, d x } } = - 2 $$ و $$ \displaystyle \int _ { { \, 1 0 0 } } ^ { { \, - 5 } } { { f \left ( x \right ) \, d x } } = 4 $$ مقدار انتگرال زیر را حساب کنید:
$$ \large \displaystyle \int _ { { \, - 5 } } ^ { { \, 1 2 } } { { f \left ( x \right ) \, d x } } $$
حل: برای حل این مثال، از ویژگی پنجم و ویژگی اول استفاده میکنیم. طبق ویژگی پنجم میتوان انتگرال را به سه انتگرال زیر شکست:
$$ \large \int _ { { \, - 5 } } ^ { { \, 1 2 } } { { f \left ( x \right ) \, d x } } = \int _ { { \, - 5 } } ^ { { \, 1 0 0 } } { { f \left ( x \right ) \, d x } } + \int _ { { \, 1 0 0 } }^ { { \, - 1 0 } } { { f \left ( x \right ) \, d x } } + \int _ { { \, - 1 0 } } ^ { { \, 1 2 } } { { f \left ( x \right ) \, d x } } $$
در ادامه، لازم است از ویژگی اول استفاده کرده و حدود بالا و پایین دو انتگرال را تغییر دهیم. بنابراین، حاصل انتگرال این مثال را میتوان به صورت زیر نوشت:
$$ \large \begin {align*} \int _ { { \, - 5 } } ^ { { \, 1 2 } } { { f \left ( x \right ) \, d x } } & = - \int _ { { \, 1 0 0 } } ^ { { \, - 5 } } { { f \left ( x \right ) \, d x } } + \int _ { { \, 100 } } ^ { { \, - 1 0 } } { { f \left ( x \right ) \, d x } } - \int _ { { \, 1 2 } } ^ { { \, - 1 0 } } { { f \left ( x \right ) \, d x } } \\ & = - 4 - 2 - 6 \\ & = - 1 2 \end {align*} $$
تفسیر انتگرال معین
دو تفسیر برای انتگرال معین وجود دارد که در اینجا آنها را بیان میکنیم.
طبق تفسیر اول، انتگرال معین، همان مساحت خالص بین منحنی $$f(x) $$ و محور $$x$$ در بازه $$ \left[ {a,b} \right] $$ است. مثلاً مساحت بین منحنی $$ f\left( x \right) = {x^2} + 1 $$ و محور $$x$$ در بازه $$ \left[ {0,2} \right] $$ برابر است با:
$$ \large \int _ { { \, 0 } } ^ { { \, 2 } } { { { x ^ 2} + 1 \, d x } } = \frac { { 1 4 } } { 3 } $$
یک تفسیر دیگر وجود دارد که گاهی «قضیه تغییر خالص» (Net Change Theorem) نامیده میشود. این تفسیر میگوید که اگر $$f(x) $$ یک کمیت باشد، آنگاه $$ f'\left( x \right) $$ نرخ تغییرات $$ f(x ) $$ است. در نتیجه، انتگرالِ
$$ \large \int _ { { \, a } } ^ { { \, b } } { { f ^ \prime \left ( x \right ) \, d x } } = f \left ( b \right ) - f \left ( a \right ) $$
مجموع تغییرات خالص $$f(x) $$ در بازه $$ \left[ {a,b} \right] $$ است. به عبارت دیگر، برای به دست آوردن تغییرات خالص یک کمیت، انتگرال معین نرخ تغییر را حساب میکنیم. میتوان مشاهده کرد که مقدار انتگرال معین، یعنی $$ f\left( b \right) - f\left( a \right) $$، در حقیقت تغییر خالص $$f(x) $$ را به ما میدهد. به عنوان یک مثال ساده، اگر $$ V\left( t \right) $$ حجم آب درون یک مخزن باشد، آنگاه انتگرالِ
$$ \large \int _ { { \, { t _ 1 } } } ^ { { \, { t _ 2} } } { { V ^ \prime \left ( t \right ) \, d t } } = V \left ( { { t _ 2 } } \right ) - V \left ( { { t _ 1 } } \right ) $$
تغییرات خالص حجم از لحظه $$t_1 $$ تا $$t_2 $$ است.
به طریق مشابه، میدانیم اگر $$ s(t)$$ تابع موقعیت یک جسم در زمان $$t$$ باشد، سرعت آن $$ v\left( t \right) = s'\left( t \right) $$ خواهد بود. بنابراین، جابهجایی جسم بین زمانهای $$t_1 $$ و $$t_2$$ برابر است با:
$$ \large \int _ { { \, { t _ 1 } } } ^ { { \, { t _ 2 } } } { { v \left ( t \right ) \, d t } } = s \left ( { { t _ 2 } } \right ) - s \left ( { { t _ 1 } } \right ) $$
در این حالت، اگر $$v(t)$$ هم مثبت و هم منفی باشد (یعنی جسم در هر دو جهت حرکت کند)، انتگرال بالا، مقدار کل مسافت طی شده را به دست نخواهد داد و فقط جابهجایی خالص را میدهد. برای آنکه کل مسافت طی شده را به دست آوریم، باید انتگرال زیر را محاسبه کنیم:
$$ \large \int _ { { \, { t _ 1 } } } ^ { { \, { t _ 2 } } } { { \left | { v \left ( t \right ) } \right | \, d t } } $$
بخش اول قضیه اساسی حسابان
در اینجا، بخش اول قضیه اساسی حسابان را بیان میکنیم. بخش اول قضیه حسابان بیان میکند که چگونه باید از انواع مشخص انتگرال معین، مشتق گرفت. این قضیه به این صورت بیان میشود که اگر $$ f(x ) $$ در بازه $$ \left[ {a,b} \right] $$ پیوسته باشد، آنگاه، تابعِ
$$ \large g \left ( x \right ) = \int _ { { \, a } } ^ { { \, x } } { { f \left ( t \right ) \, \, d t } } $$\
در بازه $$ \left[ {a,b} \right] $$ پیوسته و در $$ \left( {a,b} \right) $$ مشتقپذیر است و داریم:
$$ \large g ' \left ( x \right ) = f \left ( x \right ) $$
یک نوشتار جایگزین برای بخش مشتق، به صورت زیر است:
$$ \large \frac { d } { { d x } } \int _ { { \, a } } ^ { { \, x } } { { f \left ( t \right ) \, d t } } = f \left ( x \right ) $$
مثال ۶
مشتق هریک از توابع زیر را محاسبه کنید:
(الف) $$ \large \displaystyle g \left ( x \right ) = \int _ { { \, - 4 } } ^ { { \, x } } { { { { \bf { e } } ^ { 2 t } } { { \cos } ^ 2 } \left ( { 1 - 5 t } \right ) \, d t } } $$
با استفاده از قضیه اساسی حسابان میتوان نوشت:
$$ \large g ' \left ( x \right ) = { { \bf { e } } ^ { 2 x } } { \cos ^ 2 } \left ( { 1 - 5 x } \right ) $$
(ب) $$ \large \displaystyle \int _ { { \, { x ^ 2 } } } ^ { { \, 1 } } { { \frac { { { t ^ 4 } + 1 } } { { { t ^ 2 } + 1 } } \, d t } } $$
قبل از به کار بردن قضیه اساسی حسابان، باید مقداری عملیات ریاضی انجام دهیم. اولین کار این است که حد پایین انتگرال را به یک عدد ثابت و حد بالا را به یک متغیر تبدیل کنیم. بنابراین، با استفاده از قضایایی که در بالا بیان کردیم، داریم:
$$ \large \frac { d } { { d x } } \int _ { { \, { x ^ 2 } } } ^ { { \, 1 } } { { \frac { { { t ^ 4 } + 1 } } { { { t ^ 2 } + 1 } } \, d t } } = \frac { d } { { d x } } \left ( { - \int _ { { \, 1 } } ^ { { \,{ x ^ 2 } } } { { \frac { { { t ^ 4 } + 1 } } { { { t ^ 2 } + 1 } } \, d t } } } \right ) = - \frac { d } { { d x } } \int _ { { \, 1 } } ^ { { \, { x ^ 2 } } } { { \frac { { { t ^ 4 } + 1 } } { { { t ^ 2 } + 1 } } \, d t } } $$
اکنون باید حد بالایی انتگرال را به $$x$$ تبدیل کنیم و پس از آن از قضیه اساسی حسابان استفاده کنیم. این کار را با استفاده از قاعده زنجیرهای انجام میدهیم:
$$ \large \frac { d } { { d x } } \left ( { g \left ( u \right ) } \right ) = \frac { d } { { d u } } \left ( { g \left ( u \right ) } \right ) \, \, \frac { { d u } } { { d x } } { \mbox{ , }}\hspace {0.3in}u = f \left ( x \right ) $$
اگر تساوی $$ u = x ^ 2 $$ را در نظر بگیریم، با استفاده از قاعده زنجیرهای، داریم:
$$ \large \begin {align*} \frac { d } { { d x } } \int _ { { \, { x ^ 2 } } } ^ { { \, 1 } } { { \frac { { { t ^ 4 } + 1 } } { { { t ^ 2 } + 1 } } \, d t } } & = - \frac { d } { { d x } } \int _ { { \, 1 } } ^ { { \, { x ^ 2 } } } { { \frac { { { t ^ 4 } + 1 } } { { { t ^ 2 } + 1 } } \, d t } } \\ & = - \frac { d } { { d u } } \int _ { { \, 1 } } ^ { { \, u } } { { \frac { { { t ^ 4 } + 1 } } { { { t ^ 2 } + 1 } } \, d t } } \, \, \, \frac { { d u } } { { d x} } { \mbox { , }} \hspace {0.5in} u = { x ^ 2 } \\ & = - \frac { { { u ^ 4 } + 1 } } { { { u ^ 2 } + 1 } } \left ( { 2 x } \right ) \\ & = - 2 x \frac { { { u ^ 4 } + 1 } } { { { u ^ 2 } + 1 } } \end {align*} $$
گام آخر، نوشتن عبارت بر حسب $$x $$ است:
$$ \large \begin {align*} \frac { d } { { d x } } \int _ { { \, { x ^ 2 } } } ^ { { \, 1 } } { { \frac { { { t ^ 4 } + 1 } } { { { t ^ 2 } + 1 } } \, d t } } & = - 2 x \frac { { { { \left ( { { x ^ 2 } } \right ) } ^ 4 } + 1 } } { { { { \left ( { { x ^ 2 } } \right ) } ^ 2 } + 1 } } \\ & = - 2 x \frac { { { x ^ 8 } + 1 } } { { { x ^ 4 } + 1 } } \end {align*} $$
قاعده زنجیرهای
با استفاده از قاعده زنجیرهای میتوانیم چند فرمول کلی را برای مسائل پیچیده استخراج کنیم. عبارت زیر، قاعده زنجیرهای برای دستهای از مسائل است:
$$ \large \frac { d } { { d x } } \int _ { { \, a } } ^ { { \, u \left ( x \right ) } } { { f \left ( t \right ) \, d t } } = u ^ \prime \left ( x \right ) f \left ( { u \left ( x \right ) } \right ) $$
همچنین، میتوان فرمولی برای انتگرالهایی نوشت که حد بالای آنها یک عدد ثابت و حد پایین آنها تابعی از $$x $$ است. برای این کار میتوان حدود انتگرال بالا را جابهجا، و با قرار دادن یک منفی، اثر آن را خنثی کرد:
$$ \large \frac { d } { { d x } } \int _ { { \, v \left ( x \right ) } } ^ { { \, b } } { { f \left ( t \right ) \, d t } } = - \frac { d } { { d x } } \int _ { { \, b } } ^ { { \, v \left ( x \right ) } } { { f \left ( t \right ) \, d t } } = - v ^ \prime \left ( x \right ) f \left ( { v \left ( x \right ) } \right ) $$
در نهایت، میتوان حالتی را بیان کرد که هر دو حد بالا و پایین انتگرال، تابعی از $$ x $$ باشند:
$$ \large \int _ { { \, v \left ( x \right ) } } ^ { { \, u \left ( x \right ) } } { { f \left ( t \right ) \, d t } } = \int _ { { \, v \left ( x \right ) } } ^ { { \, a } } { { f \left ( t \right ) \, d t } } + \int _ { { \, a } } ^ { { \, u \left ( x \right ) } } { { f \left ( t \right ) \, d t } } $$
به ازای هر مقداری از $$a $$ میتوانیم انتگرال را بشکنیم. تنها لازم است توجه کنیم که $$f(a) $$ وجود داشته باشد. بنابراین، با فرض وجود $$f(a) $$، بعد از شکستن انتگرال، میتوانیم به صورت زیر از آن انتگرال بگیریم:
$$ \large \begin {align*} \frac { d } { { d x } } \int _ { { \, v \left ( x \right ) } } ^ { { \, u \left ( x \right ) } } { { f \left ( t \right ) \, d t } } & = \frac { d } { { d x } } \left ( { \int _ { { \, v \left ( x \right ) } } ^ { { \, a } } { { f \left ( t \right ) \, d t } } + \int _ { { \, a } } ^ { { \, u \left ( x \right ) } } { { f \left ( t \right ) \, d t } } } \right ) \\ & = - v ^ \prime \left ( x \right ) f \left ( { v \left ( x \right ) } \right ) + u ^ \prime \left ( x \right ) f \left ( { u \left ( x \right ) } \right ) \end {align*} $$
مثال ۷
مشتق انتگرال زیر را محاسبه کنید:
$$ \large \int _ { { \, \sqrt x } } ^ { { \, 3 x } } { { { t ^ 2 } \sin \left ( { 1 + { t ^ 2 } } \right ) \, d t } } $$
حل: از فرمول زیر برای مشتقگیری از انتگرال بالا استفاده میکنیم:
$$ \large \begin {align*} \frac { d } { { d x } } \int _ { { \, \sqrt x } } ^ { { \, 3 x } } { { { t ^ 2 } \sin \left ( { 1 + { t ^ 2 } } \right ) \, d t } } & = - \frac { 1 } { 2 } { x ^ { - \frac { 1 }{ 2 } } } { \left ( { \sqrt x } \right ) ^ 2 } \sin \left ( { 1 + { { \left ( { \sqrt x } \right ) } ^ 2 } } \right ) + \left ( 3 \right ){ \left ( { 3 x } \right ) ^ 2 } \sin \left ( { 1 + { { \left ( { 3 x } \right ) } ^ 2 } } \right ) \\ & = - \frac { 1 } { 2 } \sqrt x \sin \left ( { 1 + x } \right ) + 27 { x ^ 2 } \sin \left ( { 1 + 9 { x ^ 2 } } \right ) \end {align*} $$
بخش دوم قضیه اساسی حسابان
فرض کنید $$ f (x ) $$ در بازه $$ \left[ {a,b} \right] $$ تابعی پیوسته، و $$ F (x ) $$ پادمشتق $$f (x ) $$ باشد. آنگاه، تساوی زیر برقرار است:
$$ \large \int _ { { \, a } } ^ { { \, b } } { { f \left ( x \right ) d x } } = \left . { F \left ( x \right ) } \right | _ a ^ b = F \left ( b \right ) - F \left ( a \right ) $$
اثبات فرمول بالا، در آموزش قضیه اساسی حسابان به طور کامل ارائه شده است.
در ادامه، چند مثال را از کاربرد این قضیه برای محاسبه انتگرال معین بررسی میکنیم.
مثال ۸
حاصل انتگرال زیر را به دست آورید:
$$ \large \displaystyle \int _ { { - 3 } } ^ { 1 } { { 6 { x ^ 2 } - 5 x + 2 \, d x } } $$
حل: با استفاده از فرمول اخیر، به سادگی داریم:
$$ \large \begin{align*} \int _ { { - 3 } } ^ { 1 } { { 6 { x ^ 2 } - 5 x + 2 \, d x } } & = \left . { \left ( { 2 { x ^ 3 } - \frac { 5 } { 2 } { x ^ 2 } + 2 x } \right ) } \right | _ { - 3 } ^ 1 \\ & = \left ( { 2 - \frac { 5 } { 2 } + 2 } \right ) - \left ( { - 5 4 - \frac { { 4 5 } } { 2 } - 6 } \right ) \\ & = 8 4 \end {align*} $$
مثال ۹
انتگرال زیر را محاسبه کنید:
$$ \large \displaystyle \int _ { { \, 1 } } ^ { { \, 2 } } { { \frac { { 2 { w ^ 5 } - w + 3 } } { { { w ^ 2 } } } \, d w } } $$
حل: با استفاده از قضیه اساسی حسابان، میتوان نوشت:
$$ \large \begin {align*} \int _ { { \, 1 } } ^ { { \, 2 } } { { \frac { { 2 { w ^ 5 } - w + 3 } } { { { w ^ 2 } } } \, d w } } & = \int _ { { \, 1 } } ^ { { \, 2 } } { { \, 2 { w ^ 3 } - \frac { 1 } { w } + 3 { w ^ { - 2 } } d w } } \\ & = \left . { \left ( { \frac { 1 } { 2 } { w ^ 4 } - \ln \left | w \right | - \frac { 3 } { w } } \right ) } \right | _ 1 ^ 2 \\ & = \left ( { 8 - \ln 2 - \frac { 3 } { 2 } } \right ) - \left ( { \frac { 1 } {2 } - \ln 1 - 3 } \right ) \\ & = 9 - \ln 2 \end {align*} $$
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:











بازه انتگرلگیری را میتوان به دو زیربازه متصل به هم
[
a
,
c
]
و
[
c
,
b
]
شکست (لزومی ندارد
c
حتماً بین
a
و
b
باشد)
سلام وقتتون بخیر چطوری میتونه بینشون نباشه؟ اگه اینجوری باشه نباید کم کنیمشون از هم؟
ممنونم از لطفتون
عالی بود .مرسی.