انتگرال توابع نمایی – از صفر تا صد

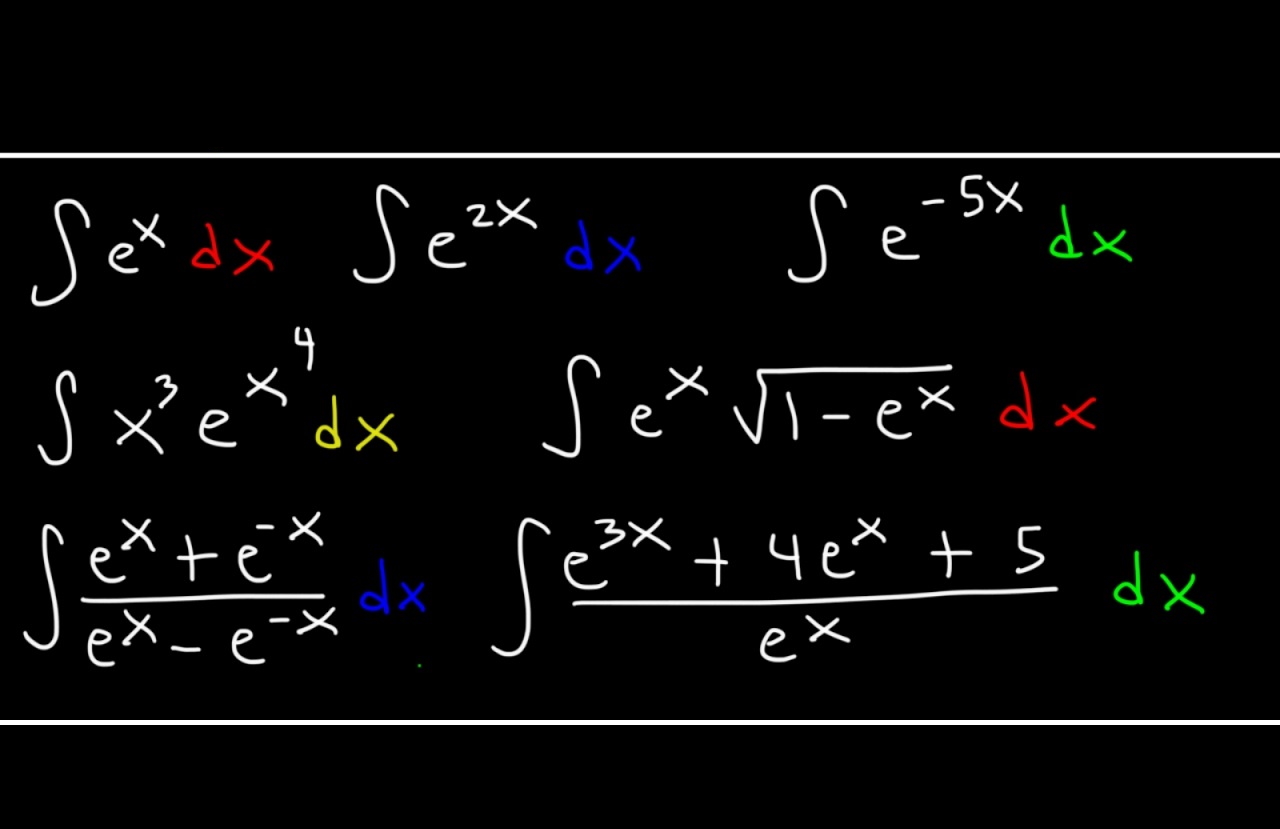
پیش‌تر در مجموعه آموزش‌های ریاضی مجله فرادرس، با مفهوم انتگرال آشنا شدیم. همچنین، مباحثی مانند انتگرال توابع مثلثاتی، انتگرال توابع لگاریتمی و انتگرال توابع رادیکالی را ارائه کردیم. در این آموزش، درباره انتگرال توابع نمایی بحث خواهیم کرد.

توابع نمایی و لگاریتمی در مواردی مانند مدلسازی رشد جمعیت، رشد سلول، رشد اقتصادی، توصیف فروپاشی رادیواکتیو، مصرف منابع و چندین مورد دیگر کاربرد فراوانی دارند.

انتگرال توابع نمایی

تابع نمایی یکی از توابع مهم است که در عملیات‌های ریاضی بسیار با آن سر و کار داریم. مشتق و انتگرال تابع نمایی $$y = e ^ x$$ برابر با خودش است.

با استفاده از فرمول‌های زیر می‌توان از توابع نمایی انتگرال گرفت:

$$\large ∫ e ^ x \, d x = e ^ x + C$$

$$\large ∫ a ^ x \, d x = \dfrac { a ^ x } { \ln a } + C$$

مثال ۱

پادمشتق تابع نمایی $$e^{−x}$$ را بیابید.

حل: از تغییر متغیر $$u = - x$$ استفاده می‌کنیم. در نتیجه، عبارت $$d u = - 1 d x$$ را داریم. با ضرب معادله $$du$$ در $$-1$$ تساوی $$-du=dx$$ را خواهیم داشت. در نتیجه، پادمشتق به صورت زیر محاسبه می‌شود:

$$\large ∫ e ^ { − x } \, d x = − ∫ e ^ u \, d u = − e ^ u + C = − e ^ { − x } + C . \nonumber$$

یک اشتباه رایج در هنگام محاسبات مربوط به نمایی‌ها این است که با نمایی $$e$$ همان‌طور رفتار کنیم که با عبارات چندجمله‌ای رفتار می‌کنیم. نمی‌توانیم از قانون توان برای نمایی $$e$$ استفاده کنیم. این موضوع زمانی که هم نمایی و هم چندجمله‌ای در یک عبارت داشته باشیم، کمی باعث سردرگمی خواهد شد. در این مورد، همیشه باید با دقت محاسبات را بررسی کنیم.

مثال ۲

پادمشتق تابع نمایی $$e^x\sqrt{1+e^x}$$ را محاسبه کنید.

حل: ابتدا توان را به صورت یک عدد گویا می‌نویسیم:

$$\large ∫ e ^ x \sqrt { 1 + e ^ x } \, d x = ∫ e ^ x ( 1 + e ^ x ) ^ { 1 / 2 } \, d x . \nonumber$$

با استفاده از تغییر متغیر $$u=1+e^x$$ و در نتیجه $$du=e^x\,dx$$، داریم:

$$\large ∫ e ^ x ( 1 + e ^ x ) ^ { 1 / 2 } \, d x = ∫ u ^ { 1 / 2 } \, d u . \nonumber$$

در نتیجه:

$$\large ∫ u ^ { 1 / 2 } \, d u = \dfrac { u ^ { 3 / 2 } }{ 3 / 2 } + C = \dfrac { 2 } { 3 } u ^ { 3 / 2 } + C = \dfrac { 2 } { 3 } ( 1 + e ^ x ) ^ { 3 / 2 } + C \nonumber$$

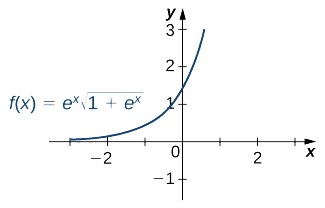
مثال ۳

حاصل انتگرال $$\displaystyle ∫3x^2e^{2x^3}\,dx$$ را به دست آورید.

حل: توان تابع نمایی را به عنوان $$u=2x^3$$ در نظر می‌گیریم و بنابراین تساوی دیفرانسیلی $$du=6x^2\,dx$$ را داریم. تابع اصلی شامل عامل $$3 x ^ 2$$ و نه $$6 x ^ 2$$ است. با ضرب دو طرف معادله در $$\dfrac{1}{2}$$، انتگرالده برحسب $$u$$ معادل با انتگرالده برحسب $$x$$ خواهد بود. بنابراین:

$$\large ∫ 3 x ^ 2 e ^ { 2 x ^ 3 } \, d x = \frac { 1 } { 2 }∫ e ^ u \, d u .$$

با انتگرال‌گیری از عبارت برحسب $$u$$ و جایگذاری جملات برحسب $$x$$، خواهیم داشت:

$$\large \frac { 1 } { 2 } ∫ e ^ u \, d u = \frac { 1 } { 2 } e ^ u + C = \frac { 1 } { 2 } e ^ 2 x ^ 3+ C .$$

مثال ۴

انتگرال معین زیر را با استفاده از تغییر متغیر حل کنید:

$$\large ∫ ^ 2 _ 1 \dfrac { e ^ { 1 / x } } { x ^ 2 } \, d x . \nonumber$$

حل: باید مسئله را بازنویسی کنیم. ابتدا نمایی را طوری می‌نویسیم که $$x$$ در توان آن وجود داشته باشد. عبارت $$x ^ 2$$ را با منفی کردن توان آن از مخرج به صورت می‌آوریم:

$$\large ∫ ^ 2 _ 1 \dfrac { e ^ { 1 / x } }{ x ^ 2 } \, \, d x = ∫^ 2 _ 1 e ^ { x ^ { − 1 } } x ^ { − 2 } \, d x . \nonumber$$

توان نمایی را $$u=x^{−1}$$ در نظر می‌گیریم. بنابراین، داریم:‌

$$\large d u = − x ^ { −2 } \, d x \nonumber$$

$$\large − d u = x ^ { − 2 } \, d x . \nonumber$$

با بیرون آوردن علامت منفی، مسئله به صورت زیر خواهد بود:‌

$$\large − ∫ e ^ u \, d u . \nonumber$$

بنابراین، حدود انتگرال به صورت زیر تغییر خواهند کرد:‌

$$\large u = ( 1 ) ^ { − 1 } = 1 \nonumber$$

$$\large u = ( 2 ) ^ { − 1 } = \dfrac { 1 } { 2 } . \nonumber$$

در نهایت، انتگرال به صورت زیر محاسبه می‌شود:‌

$$\large − ∫ ^ { 1 / 2 } _ 1 e ^ u \, d u = ∫ ^ 1 _ { 1 / 2 } e ^ u \, du = e ^ u \big | ^ 1 _ { 1 / 2 } = e − e ^ { 1 /2 } = e − \sqrt { e } . \nonumber$$

انتگرال‌هایی با لگاریتم طبیعی

انتگرال‌گیری از توابعی به فرم $$f(x)=\dfrac{1}{x}$$ و $$f(x) = x^{−1}$$ منجر به لگاریتم طبیعی قدر مطلق $$x$$ می‌شود. در واقع، می‌توان از فرمول زیر برای انتگرال‌هایی که توان $$-1$$ دارند استفاده کرد:

$$\large ∫ \frac { 1 } { x } \, d x = \ln | x | + C$$

در حقیقت، می‌توانیم این فرمول را برای انتگرالده‌های کسری که در آن‌ها صورت مشتق مخرج است تعمیم دهیم. در واقع، با استفاده از قاعده زنجیره‌ای می‌توانیم مشتق $$y = \ln[u(x)]$$ را به صورت زیر محاسبه کنیم:

$$\large \frac { d } {d x} \left ( \ln [ u ( x ) ] \right ) = \frac { 1 } { u ( x ) } \cdot u' ( x ) = \frac { u' ( x ) } { u (x ) }$$

بنابراین، فرمول زیر یک فرمول بسیار مهم و کاربردی در حل انتگرال است:

$$\large ∫ \frac { u' ( x ) } { u ( x ) } \, d x =\ln | u ( x ) | + C$$

مثال ۵

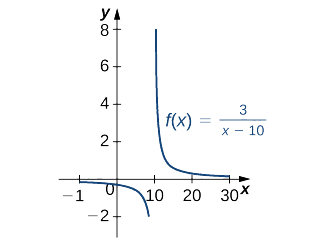
پادمشتق تابع $$\dfrac { 3 } { x − 1 0 }$$ را به دست آورید.

حل: ابتدا ضریب $$3$$ را از انتگرال بیرون آورده، سپس از قانون $$u'/u$$ استفاده می‌کنیم:

$$\large ∫ \dfrac { 3 } { x − 10 } \, d x = 3 ∫ \dfrac { 1 } { x − 1 0 } \, d x = 3 ∫ \dfrac { d u } { u } = 3 \ln | u | + C = 3 \ln | x − 1 0 | + C , \quad x ≠ 1 0 . \nonumber$$

شکل زیر نمودار تابع را نشان می‌دهد.

مثال ۶

پادمشتق تابع زیر را به دست آورید:

$$\large \dfrac { 2 x ^ 3 + 3 x } { x ^ 4 + 3 x ^ 2 } . \nonumber$$

حل: از تغییر متغیر استفاده می‌کنیم. متغیر $$u=x^4+3x^2$$ را در نظر می‌گیریم که در نتیجه آن، $$du=(4x^3+6x)\,dx$$. در رابطه $$du$$ از $$2$$ فاکتور می‌گیریم. بنابراین، داریم:

$$\large d u = ( 4 x ^ 3 + 6 x ) \, d x = 2 ( 2 x ^ 3 + 3 x ) \, d x \nonumber$$

$$\large \dfrac { 1 } { 2 } \, d u = ( 2 x ^ 3 + 3 x ) \, d x . \nonumber$$

انتگرالده را برحسب $$u$$ می‌نویسیم:

$$\large ∫ \frac { 2 x ^ 3 + 3 x } { x ^ 4 + 3 x ^ 2 } \, d x = \dfrac { 1 } { 2 } ∫ \frac { 1 } { u } \, d u . \nonumber$$

بنابراین، خواهیم داشت:‌

$$\large \dfrac { 1 } { 2 } ∫ \frac { 1 } { u } \, d u = \dfrac { 1 } { 2 } \ln | u | + C = \dfrac { 1 } { 2 } \ln ∣ x ^ 4 + 3x ^ 2 ∣ + C . \nonumber$$

مثال ۷

حاصل انتگرال معین زیر را به دست آورید:

$$\large ∫ ^ { \pi / 2 } _ 0 \dfrac { \sin x } { 1 + \cos x } \, d x . \nonumber$$

حل: برای حل این مثال، از تغییر متغیر $$u=1+\cos x$$ و در نتیجه $$du=−\sin x\,\,dx$$ استفاده می‌کنیم. انتگرال را بر حسب متغیر جدید $$u$$ بازنویسی می‌کنیم. حدود انتگرال‌گیری جدید به صورت زیر خواهند بود:

$$\large u = 1 + \cos ( 0 ) = 2$$

$$\large u = 1 + \cos ( \dfrac { π } { 2 } ) = 1 .$$

در نتیجه، خواهیم داشت:

$$\large \begin {align*} ∫ ^ { \pi / 2 } _ 0 \dfrac { \sin x }{ 1 + \cos x } & = − ∫ ^ 1 _ 2 \frac { 1 } { u } \, d u = ∫ ^ 2 _ 1 \frac { 1 } { u } \, d u \\ & = \ln | u | \, \bigg | ^ 2 _ 1 = [ \ln 2 − \ln 1 ] = \ln 2 \end {align*}$$

مثال ۸

حاصل انتگرال $${ \int _{ { - { 1 } } } ^ { { 1 } } } \frac { { { \left . { d } { x } \right . } } } { { { e } ^ { { { 2 } - { 3 } { x } } } } }$$ را محاسبه کنید.

حل: از آنجایی که $$-(2-3x)=2x-2$$، می‌توانیم مخرج را به صورت آورده و انتگرال را به صورت زیر بنویسیم:

$$\large { \int _ { { - { 1 } } } ^ { {1 }} } { e } ^ { {- { \left ( { 2 } -{ 3 } {x } \right ) } } } { \left . { d } { x } \right . } = { \int _ { - { { 1 } } } ^ { { 1 } } } { e } ^ { { { 3 } { x } - { 2 } } } { \left . { d } { x } \right . }$$

با استفاده از تغییر متغیر $$u=3x-2$$ و در نتیجه، $$du=3dx$$، داریم:

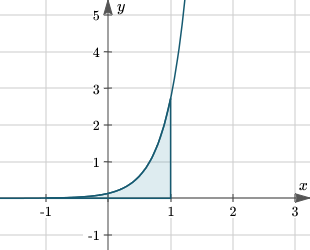
$$\large { \int _ { - { { 1 } } } ^ { { 1} } } { e } ^ { { { 3 }{ x } - { 2 } } } { \left . { d } { x } \right . } = \frac { 1 } {{ 3 } } { { \left [ { e } ^ { { { 3 } { x } - { 2 } } } \right ] } _ { - { { 1 } } } ^ { { 1 } } } = \frac { 1 } { { 3 } } { \left [ { e } ^ { 1 } -{ e } ^ { - { { 5 } } } \right ] } = { 0 . 9 0 3 8 }$$

نمودار منحنی $${ y } = \frac { 1 } { { e } ^ { { { 2 } - { 3 } { x } } } }$$ در شکل زیر نشان داده شده است.

حالت‌های خاص

در این بخش، چند حالت خاص مربوط به محاسبه انتگرال توابع نمایی را بررسی می‌کنیم.

• حالت خاص ۱: اگر انتگرال به صورت $$\int e ^ x \big ( f ( x ) + f' ( x ) \big ) \, d x$$ باشد، حاصل آن برابر با $$e ^ x f ( x ) + C$$ است.
• حالت خاص ۲: اگر انتگرال به صورت $$I = \int e ^ { a x } \cos ( b x + c )$$ باشد، حاصل آن به صورت زیر خواهد بود:

$$\large I = \dfrac { e ^ { a x } \big ( a \cos ( b x + c ) + b \sin ( b x + c ) \big ) } { a ^ 2 + b ^ 2 } .$$

برای اثبات این رابطه، می‌توان نوشت:

$$\large \begin {aligned} I & = \int e ^ { a x } \cos ( b x + c ) d x \\ & = \cos ( b x + c ) \frac { e ^ { a x } } { a } + \frac { b } { a } \int e ^ { a x } \sin ( b x + c ) d x \\ & = \cos ( b x + c ) \frac { e ^ { a x } } { a } + \frac { b } { a } \left ( \frac { e ^ { a x } } { a } \sin ( b x + c ) - \frac { b } { a } \int e ^ { a x } \cos ( b x + c ) \right ) d x \\ & = \frac { e ^ { a x } ( a \cos ( b x + c ) + b \sin ( b x + c ) ) } { a ^ { 2 } } - \frac { b ^ { 2 } } { a ^{ 2 } } I \end {aligned}$$

بنابراین:

$$\large \begin {aligned} I \left ( 1 + \frac { b ^ 2 } { a ^ 2 } \right ) & = \frac { e ^ { a x } \big ( a \cos ( b x + c ) + b \sin ( b x + c ) \big ) } { a ^ 2 } \\ \Rightarrow I & = \frac { e ^ { a x } \big ( a \cos ( b x + c ) + b \sin ( b x + c ) \big ) } { a ^ 2 + b ^ 2 } . \end{aligned}$$

انتگرال $$I = \int e ^ { a x } \sin ( b x + c )$$ به روش مشابه حل می‌شود.

• حالت خاص ۳: انتگرالی به فرم $$\int \frac { a e ^ x + b e ^ { - x } } { p e ^ x + q e ^ { - x } } d x$$ که در حقیقت به شکل $$\text {(NUM)} = \alpha \text {(DEN)} + \beta \frac { d } { dx } \text {(DEN)}$$ است ($$\text {(NUM)}$$ نشان‌ دهنده صورت و $$\text {(DEN)}$$ نشان دهنده مخرج انتگرالده است)، به صورت عادی محاسبه می‌شود.

مثال ۹

حاصل انتگرال نامعین زیر را به دست آورید.

$$\large \int e ^ x \big ( \sin ( x ) + \cos ( x ) \big ) \, d x$$

حل: همان‌طور که می‌بینیم، این انتگرال به فرم $$\int e ^ x \big ( f ( x ) + f' ( x ) \big ) \, d x$$ است که در آن، $$f(x)=\sin (x)$$. بنابراین، حاصل این انتگرال برابر است با:

$$\large e ^ x \sin ( x ) + C .$$

مثال ۱۰

انتگرال زیر را محاسبه کنید.

$$\large \int e ^ { 2 x } \cos ( 5 x + 3 ) \, d x$$

حل: طبق رابطه‌ای که در بالا آن را معرفی کردیم، حاصل انتگرال برابر است با:

$$\large \frac { e ^ { 2 x } \big ( 2 \cos ( 5 x + 3) + 5 \sin ( 5 x + 3 ) \big ) } {2 9 } + C .$$

مثال ۱۱

حاصل انتگرال نامعین زیر را به دست آورید.

$$\large \int \frac { 2 e ^ x + 3 e ^ { - x } } { e ^ x - 5 e ^ { -x } } \, d x$$

حل: می‌توانیم تساوی زیر را بنویسیم:

$$\large 2 e ^ x + 3 e ^ { - x } = \alpha ( e ^ x - 5 e ^ { - x } ) + \beta ( e ^ x + 5 e ^ { - x } )$$

با مقایسه ضرایب $$e^x$$ و $$e^{-x}$$، به معادلات $$\alpha + \beta = 2$$ و $$\alpha - \beta = - \frac{3}{5}$$ می‌رسیم که $$\alpha = \frac{7}{10}$$ و $$\beta = \frac{13}{10}$$ را نتیجه می‌دهند. بنابراین، می‌توان نوشت:

$$\large \int \frac { 2 e ^ x + 3 e ^ { - x } } { e ^ x - 5 e ^ { - x } } d x = \alpha \int d x + \beta \int \frac { e ^ x + 5 e ^ { - x } } {e ^ x - 5 e ^ { - x } } d x . \qquad (*)$$

با در نظر گرفتن $$e ^ x - 5 e ^ {-x} = t$$ و در نتیجه، $$( e ^ x + 5 e ^ { - x } ) d x = d t$$، خواهیم داشت:‌

$$\large \begin {aligned} ( * ) & = \frac 7 { 1 0 } \int d x + \frac { 1 3 } { 1 0 } \int \frac { d t } { t } \\ & = \frac { 7 x } { 1 0 } + \frac { 1 3 } { 1 0 } \ln | t | + C \\ & = \frac { 7 x } { 1 0 } + \frac { 1 3 } { 1 0 } \ln \big | e ^ x – 5 e ^ { – x } \big | + C \end {aligned}$$

که در آن، $$C$$ ثابت انتگرال‌گیری است.

فهرست انتگرال‌های نمایی

در این بخش، فهرستی از انتگرال‌های توابع نمایی مختلف را ارائه می‌کنیم.

انتگرال نامعین

انتگرال‌های نامعین، توابع پادمشتق هستند و یک عدد ثابت (ثابت انتگرال‌گیری) به سمت راست فرمول آن‌ها افزوده می‌شود. برای سادگی، ثابت انتگرال‌گیری را در فرمول‌ها نیاورده‌ایم.

انتگرال‌هایی که چندجمله‌ای دارند

$$\large \int x e ^ { c x } \, d x = e ^ { c x } \left ( \frac { c x - 1 }{ c ^ { 2 } } \right )$$

$$\large \int x ^ 2 e ^ { c x } \, d x = e ^ { c x } \left ( \frac { x ^2 } {c } - \frac { 2 x } { c ^ 2 } + \frac { 2 } { c ^ 3 } \right )$$

$$\large \begin {align} \int x ^ n e ^ { c x } \, d x & = \frac { 1 } { c } x ^ n e ^ { c x } - \frac { n } { c } \int x ^ { n - 1 } e ^ { c x } \, d x \\ & = \left ( \frac { \partial } { \partial c } \right ) ^ n \frac { e ^ { c x } } { c } \\ & = e ^ { c x } \sum _ { i = 0 } ^ n ( - 1 ) ^ i \frac { n ! }{ ( n - i ) ! c ^ { i +1 } }x ^ { n - i } \\ & = e ^ { c x } \sum _ { i = 0 } ^ n ( - 1 ) ^ { n - i } \frac { n ! } { i! c ^ { n - i + 1} } x^ i \end {align}$$

$$\large \int \frac { e ^ { c x } } { x } \, d x = \ln | x | + \sum _ { n = 1 } ^ \infty \frac { ( c x ) ^ n } { n \cdot n ! }$$

$$\large \int \frac { e ^ { c x } } { x ^ n } \, d x = \frac { 1 } { n- 1 } \left ( - \frac { e ^ { c x } } {x ^ { n - 1 } } + c \int \frac { e ^{ c x } } { x ^ { n - 1} } \, d x \right ) \qquad \text{(for } n \neq 1 \text {)}$$

انتگرال‌هایی که فقط تابع نمایی دارند

$$\large \int f' ( x ) e ^ { f ( x ) } \, d x = e ^ { f ( x ) }$$

$$\large \int e ^ { c x } \, d x = \frac { 1 } { c } e ^ { c x }$$

$$\large \int a ^ { c x } \, d x = \frac { 1 } { c \cdot \ln a } a ^ { c x } \qquad \text{ for } a > 0 , \ a \ne 1$$

انتگرال‌هایی که توابع نمایی و مثلثاتی دارند

$$\large \begin {align} \int e ^ { c x } \sin b x \, d x & = \frac { e ^ { c x } } { c^ 2 + b ^ 2 } ( c \sin b x - b \cos b x ) \\ & = \frac { e ^ { c x} } { \sqrt { c ^ 2 + b ^ 2 } } \sin ( b x -\phi ) \qquad \text {where } \cos ( \phi ) = \frac { c } { \sqrt { c ^ 2 + b ^ 2 } } \end {align}$$

$$\large \begin {align} \int e ^ { c x } \cos b x \, d x & = \frac { e ^ { c x} } { c ^ 2 + b ^2 } ( c \cos b x + b \sin b x ) \\ & = \frac { e ^ { c x } } { \sqrt { c ^ 2+ b ^ 2 } } \cos ( b x -\phi ) \qquad \text {where } \cos ( \phi ) = \frac { c } { \sqrt { c ^ 2 + b^ 2 }} \end {align}$$

$$\large \int e ^ { c x } \sin ^ n x \, d x = \frac { e ^ { c x } \sin ^ { n - 1 } x } { c ^ 2 + n ^ 2 } ( c \sin x - n \cos x) + \frac { n ( n - 1 ) } { c ^ 2 + n ^ 2 } \int e ^ { c x } \sin ^ { n - 2 } x \, d x$$

$$\large \int e ^ { c x } \cos ^ n x \, d x = \frac { e ^ { c x } \cos ^ { n - 1 } x} { c ^ 2 + n ^ 2 } ( c \cos x + n \sin x ) + \frac { n ( n - 1 ) } { c ^ 2 + n ^ 2 } \int e ^ { c x } \cos ^ { n - 2 } x \, d x$$

انتگرال‌هایی که تابع خطا دارند

در فرمول‌های زیر، $$\text{erf}$$ تابع خطا و $$\text{Ei}$$ انتگرال نمایی است.

$$\large \int e ^ { c x } \ln x \, d x = \frac { 1 }{ c } \left ( e ^ { c x } \ln | x | - \operatorname { E i } ( c x ) \right )$$

$$\large \int x e ^ { c x ^ 2 } \, d x = \frac { 1 } { 2 c } e ^ { c x ^ 2 }$$

$$\large \int e ^ { - c x ^ 2 } \, d x = \sqrt { \frac { \pi } { 4 c } } \operatorname {erf} ( \sqrt { c } x )$$

$$\large \int x e ^ { - c x ^ 2 } \, d x = - \frac { 1 } { 2 c } e ^ { - c x ^ 2 }$$

$$\large \int \frac { e ^ {- x^ 2 } } { x ^ 2 } \, d x = -\frac { e ^ {- x ^ 2 } } {x } - \sqrt { \pi } \operatorname {erf} ( x )$$

$$\large \int { \frac { 1 } { \sigma \sqrt { 2 \pi } } e ^ { -\frac { 1 } { 2 } \left ( \frac { x - \mu } { \sigma } \right ) ^ 2 }} \ , d x = \frac { 1 } {2 } \operatorname {erf} \left ( \frac { x - \mu }{ \sigma \sqrt { 2 } } \right )$$

سایر انتگرال‌ها

$$\large \int e ^ { x ^ 2 } \, d x = e ^ { x ^ 2 } \left ( \sum _ { j = 0 } ^ { n - 1 } c _ { 2 j } \frac { 1 } { x ^ { 2 j + 1 } } \right ) + ( 2 n - 1 ) c _ { 2 n- 2 } \int \frac { e ^{ x ^ 2 } } { x ^ {2 n }} \, d x \quad \text {valid for any } n > 0 ,$$

که در آن، $$c _ { 2 j } = \frac { 1 \cdot 3 \cdot 5 \cdots ( 2 j - 1) }{ 2 ^ { j + 1 } } = \frac { ( 2 j ) ! } {j ! 2 ^ { 2 j + 1 } }$$.

$$\large { \int \underbrace { x ^ { x ^ { \cdot ^ { \cdot ^ { x } } } }} _ m d x = \sum _ { n = 0 } ^ m \frac { ( - 1) ^ n ( n + 1 ) ^{ n - 1 } }{ n ! } \Gamma ( n + 1 , - \ln x ) + \sum _ { n = m + 1 } ^ \infty ( - 1) ^ n a _ { m n } \Gamma ( n + 1 , - \ln x ) \qquad \text{(for }x> 0\text{)}}$$

که در آن،

$$\large a _ { m n } = \begin {cases} 1 & \text {if } n = 0, \\ \\ \dfrac { 1 } { n ! } & \text {if } m = 1 , \\ \\ \dfrac { 1 } { n } \sum _ { j = 1 } ^ { n } j a _ { m , n -j } a _ {m - 1 , j - 1 } & \text {otherwise} \end{cases}$$

و $$\Gamma(x,y)$$ تابع گاما است.

$$\large \int \frac { 1 } { a e ^ { \lambda x } + b } \, d x = \frac { x } { b } - \frac { 1 } { b \lambda } \ln \left ( a e ^ { \lambda x } + b \right )$$

$$\large \int \frac { e ^ { 2 \lambda x } } { a e ^ { \lambda x } + b } \, d x = \frac { 1 } { a ^ 2 \lambda } \left [ a e ^ { \lambda x } + b - b \ln\left ( a e ^ {\lambda x} + b \right) \right]$$

$$\large \int \frac { a e ^ { c x} - 1 } { b e ^ { c x } - 1 } \, d x = \frac { ( a - b ) \log ( 1 - b e^ { c x} ) } { b c} + x .$$

انتگرال‌های معین

$$\large \begin {align} \int _ 0 ^ 1 e ^ { x \cdot \ln a + ( 1 - x ) \cdot \ln b } \, dx & = \int_0^1 \left ( \frac { a } { b } \right ) ^ { x} \cdot b\,dx \\ & = \int _ 0 ^ 1 a ^ { x} \cdot b ^ { 1 - x } \, d x \\ & = \frac { a - b } { \ln a - \ln b } \qquad\text{for } a > 0,\ b > 0,\ a \neq b \end{align}$$

$$\large \int _ 0 ^ { \infty } e ^ { - a x } \, d x = \frac { 1 } { a } \quad ( \operatorname { R e } ( a ) > 0 )$$

$$\large \int _ 0 ^ { \infty } e ^ { - a x ^ 2 } \, d x = \frac { 1 } { 2 } \sqrt { \pi \over a } \quad (a>0)$$

$$\large \int _ { - \infty } ^ { \infty } e ^ { - a x ^ 2 } \, d x = \sqrt { \pi \over a } \quad ( a > 0 )$$

$$\large \int _ { - \infty } ^ { \infty } e ^ { - a x ^ 2 + b x } \, d x = \sqrt { \pi \over a } e^ { \tfrac { b ^ 2 } { 4a } } \quad(a > 0)$$

$$\large \int _ { - \infty } ^ { \infty } e ^ { - a x ^ 2 } e ^ { - 2b x } \, d x = \sqrt { \frac { \pi } { a } } e ^ { \frac { b ^2 } { a } } \quad ( a > 0 )$$

$$\large \int _ { - \infty } ^ { \infty } x e ^ { - a ( x - b ) ^ 2 } \, d x = b \sqrt { \frac { \pi } { a } } \quad ( \operatorname { R e } ( a ) >0 )$$

$$\large \int _ { - \infty } ^ { \infty } x e ^ { - a x ^2 + b x } \, d x = \frac { \sqrt { \pi } b } { 2 a^ { 3 / 2 } } e ^ { \frac { b ^ 2 } { 4 a } } \quad ( \operatorname { R e } ( a ) > 0 )$$

$$\large \int _ { - \infty } ^ { \infty} x ^ 2 e ^ { - a x ^ 2 } \, d x = \frac { 1 } { 2 } \sqrt { \pi \over a ^ 3 } \quad ( a > 0 )$$

$$\large \int _ { - \infty } ^ { \infty } x ^ 2 e ^ { - a x ^ 2 + b x } \, d x = \frac { \sqrt { \pi } ( 2a + b ^ 2) }{ 4 a^ { 5 / 2} } e ^ { \frac { b ^ 2 }{ 4a } } \quad ( \operatorname{Re}(a)>0)$$

$$\large \int _ { - \infty } ^ { \infty } x ^ 3 e ^ { - a x ^ 2 + b x } \, d x = \frac { \sqrt { \pi } ( 6 a + b ^2 ) b} { 8 a ^ {7 / 2} } e ^ { \frac { b ^ 2 } { 4a } } \quad (\operatorname{Re}(a)>0)$$

$$\large \int _ 0 ^ { \infty } x ^ { n } e ^ {- a x ^ 2 } \, d x = \begin {cases} \dfrac { \Gamma \left ( \frac { n + 1 } { 2 } \right ) }{ 2 \left ( a ^ \frac { n + 1 } { 2 } \right ) } & ( n >- 1 , \ a > 0) \\ \\ \dfrac { ( 2 k - 1 ) ! ! } {2 ^ { k +1 } a ^ k } \sqrt { \dfrac { \pi } { a } } & ( n = 2 k , \ k \text { integer} , \ a > 0 ) \ \text {(!! is the double factorial)} \\ \\ \dfrac{k!}{2(a^{k+1})} & (n=2k+1,\ k \text{ integer},\ a>0) \end{cases}$$

$$\large \int _ 0 ^ { \infty } x ^ n e ^ { - a x } \, d x = \begin {cases} \dfrac { \Gamma ( n + 1 )} { a ^ { n+ 1 } } & ( n > - 1 , \ a > 0 ) \\ \\ \dfrac { n ! } { a ^ { n + 1 }} & (n = 0 , 1 , 2 ,\ldots,\ a>0) \end{cases}$$

$$\large \int _ 0 ^ { 1 } x ^n e ^ {- a x } \, d x = \frac { n ! }{ a ^{ n + 1 } } \left[ 1 - e^ { - a } \sum _ { i = 0 } ^{ n } \frac{a^i}{i!} \right]$$

$$\large \int _ 0 ^ \infty e ^ { - a x ^ b } d x = \frac { 1 } {b } \ a ^ { - \frac { 1 } { b } } \Gamma \left ( \frac { 1 } { b } \right )$$

$$\large \int _ 0 ^ \infty x ^ n e ^ { -ax ^ b } d x = \frac { 1 } {b } \ a ^ { - \frac { n +1 } { b} } \Gamma \left ( \frac { n +1 } { b } \right )$$

$$\large \int_0^{\infty} e^{-ax}\sin bx\,dx = \frac{b}{a^2+b^2} \quad (a>0)$$

$$\large \int _ 0 ^ { \infty } e ^ { - a x } \cos b x \, d x = \frac { a } {a ^ 2 + b ^2 } \quad ( a > 0 )$$

$$\large \int _ 0 ^ { \infty } x e ^ { - a x } \sin b x \, d x = \frac { 2 ab } { ( a ^ 2 + b ^2 ) ^ 2} \quad ( a > 0 )$$

$$\large \int _ 0 ^ { \infty } x e ^ { - a x } \cos b x \, d x = \frac { a ^2 - b ^ 2 }{ ( a^ 2 + b ^ 2 ) ^ 2 } \quad (a>0)$$

$$\large \int _ 0 ^ { 2 \pi } e ^ { x \cos \theta } d \theta = 2 \pi I_0(x)$$

$$\large \int _ 0 ^ { 2 \pi } e ^ { x \cos \theta + y \sin \theta} d \theta = 2 \pi I _ 0 \left( \sqrt{x^2 + y^2} \right)$$

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• انتگرال گاوسی — از صفر تا صد
• انتگرال دوگانه — به زبان ساده
• تقلب نامه (Cheat Sheet) فرمول های انتگرال

^^