کسینوس چیست و چگونه محاسبه می شود؟ – به زبان ساده
در مطالب دیگر از مجله فرادرس با کسینوس و سینوس به عنوان توابع مثلثاتی آشنا شدهاید. کسینوس به همراه بقیه توابع مثلثاتی در ریاضیات به نسبتهای مثلثاتی شهرت دارند. در این نوشتار به طور اختصاصی به تابع یا نسبت مثلثاتی کسینوس میپردازیم و خصوصیات آن را مورد بررسی قرار میدهیم. البته میدانید که سینوس و کسینوس هر دو با یکدیگر، به صورت اجتناب ناپذیری در ارتباط هستند. به این معنی که با دانستن هر یک از این مقادیر برای یک زاویه، میتوانیم دیگری را بدست آوریم. در مباحث ریاضی دبیرستان با سینوس و کسینوس آشنا شدهاید ولی تا آخرین گامهای تحصیلی در دانشگاه نیز با این گونه توابع بخصوص در زمانی که با نوسان و تناوب سروکار داشته باشید، مواجه خواهید شد. در فیزیک و مکانیک، شیمی و حتی علوم اقتصادی نیز ردپایی از این توابع پیدا خواهید کرد.

به عنوان پیشزمینه در معرفی توابع مثلثاتی بهتر است نوشتارهای جدول دایره مثلثاتی چیست؟ – روش محاسبه + حل مثال و تانژانت و کتانژانت — نسبتهای مثلثاتی به زبان ساده را مطالعه کنید. همچنین خواندن مطالب سینوس، کسینوس و تانژانت یک زاویه — به زبان ساده و روابط مثلثاتی — فرمول های مثلثاتی و روابط مهم | به زبان ساده نیز خالی از لطف نیست.
نسبت مثلثاتی کسینوس
از این جهت کسینوس و سینوس را به عنوان نسبتهای مثلثاتی میشناسیم که برپایه مثلث و زاویههای آن ساخته شدهاند. همانطور که میدانید، هر مثلث سه ضلع دارد که از برخورد این اضلاع، سه زاویه نیز پدید میآیند. مثلث، شکلی ساده بوده و پایهای برای ایجاد شکلهای هندسی دیگر است. شاید بتوان به گفت که به کمک مثلثها، میتوان هر شکل محدب دیگر را ساخت.
پایه و اساس مثلثات، «مثلث قائمالزاویه» (Right-angled Triangle)، است. در تصویر زیر یک مثلث قائمالزاویه را میبینید که زاویه قائمه آن به صورت یک مربع () دیده میشود که محل تقاطع دو ضلع BC و AC است. به یاد داشته باشید که مجموع زاویههای داخلی یک مثلث ۱۸۰ درجه است. پس میتوان نتیجه گرفت مجموع دو زاویه B و A در شکل پایین با زاویه C برابر است. در تصویر زیر، اسامی راسها را با زاویهها، یکسان در نظر گرفتهایم.
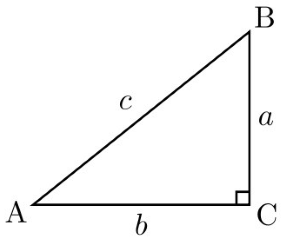
نکته: همانطور که میدانید، توابع یا نسبتهای مثلثاتی مانند سینوس و کسینوس یا تانژانت و کتانژانت، برای زاویهها (نه برای راسها) تعریف شده و به کار میروند. ولی جالب است که محاسبه این نسبتها براساس طول اضلاع مثلث مربوط به زاویه صورت میگیرد.
کسینوس یک زاویه در مثلث قائم الزاویه براساس اندازه ضلع مجاور به زاویه و طول وتر آن نوشته میشود. به یاد دارید که به طولانیترین ضلع مثلث قائم الزاویه، وتر گفته میشود. اگر زاویه را با نماد نشان دهیم، تابع کسینوس به صورت زیر نوشته شده و با عبارت «کسینوس زاویه تتا»، خوانده میشود.
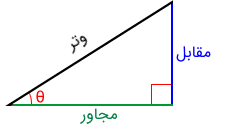
در تصویر بالا، اضلاع مثلث را برحسب محل قرارگیری آنها با زاویه تِتا () مشخص کردهایم. به این ترتیب عبارتهای زیر را برایشان در نظر میگیریم.
- ضلع رو به رو به زاویه که از این به بعد آن را ضلع مقابل مینامیم.
- طولانی ترین طول از اضلاع مثلث که آن را در این متن، وتر مثلث قائمالزاویه نامگذاری خواهیم کرد. این ضلع مجاور به زاویه نیز هست.
- ضلعی که یکی از بازوهای زاویه را میسازد و مجاور به آن زاویه نیز هست و به همین دلیل نیز ضلع مجاور نامیده میشود.
به کمک این اضلاع، مقدار کسینوس زاویه به شکل زیر قابل محاسبه است.
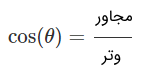
نکته: به جز زاویه قائمه، وتر به عنوان یکی از اضلاع دو زاویه دیگر محسوب میشود.
توابع مثلثاتی دیگر زاویه را میتوان به همین ترتیب نیز تعریف کرد. به عنوان مثال، سینوس زاویه نسبت بین ضلع مقابل به وتر خواهد بود. از طرفی تانژانت این زاویه همان نسبت بین دو ضلع مقابل و مجاور به زاویه در مثلث قائمالزاویه محسوب میشود.
در بخش بعدی تعریف توابع مثلثاتی، مانند کسینوس یا سینوس زاویه، از دایره مثلثاتی کمک میگیریم. پس بهتر است ابتدا با دایره مثلثاتی آشنا شده و ویژگیهای آن را بشناسیم. کار با دایره مثلثاتی، تناوب و همچنین ارتباط بین نسبتهای مثلثاتی و زاویه را بهتر نشان میدهد.
تعریف دایره مثلثاتی
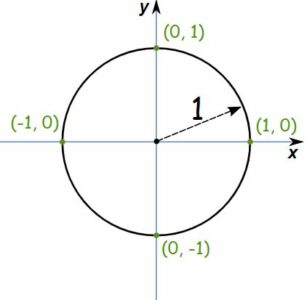
یک دایره با مرکز (0 ، 0) و شعاع یک (یک واحد) را در نظر بگیرید. در تصویر زیر چنین دایرهای قابل مشاهده است.
شعاع این دایره ممکن است یک متر، یک کیلومتر و ... باشد ولی آنچه اهمیت دارد، نسبتهایی است که در این دایره وجود دارد. از آنجایی که نسبت مانند درصد، بدون واحد است، بزرگی یا کوچکی دایره (واحد اندازهگیری آن) در اندازه نسبتهای مثلثاتی، تاثیری ندارد.
پاره خطی را در نظر بگیرید که از مبدا دایره مثلثاتی شروع شده و با دایره برخورد کرده است. این خط، نسبت به محور افقی، یک زاویه ایجاد خواهد کرد که آن را مینامیم. براساس همین پاره خط و دایره مثلثاتی، همه نسبت مثلثاتی مانند کسینوس تعریف میشوند. همانطور که میدانید، دایره مثلثاتی براساس تقسیمبندی که روی محورها ایجاد میشود به چهار بخش یا چهار ربع، تقسیم میشود. در ادامه این بخشبندیها را معرفی و براساس محل قرارگیری زاویه در هر یک از این ربعها، ویژگیهای نسبتهای مثلثاتی را بازگو خواهیم کرد.
به تصویر زیر دقت کنید که در آن طولهایی را مشخص کردهایم که براساس آن، سینوس و کسینوس زاویهها تعیین و تعریف میشوند. البته محورهای مختصات نیز در این تصویر به خوبی مشخص شده است. محور افقی با و محور عمودی با حرف دیده میشود. میدانید که در مختصات دکارتی، محورها بر هم عمود هستند. بنابراین شکلی که از زاویهای تشکیل شده در دایره مثلثاتی ساخته میشود، یک مثلث قائمالزاویه است.
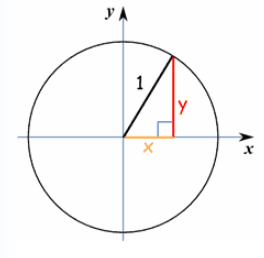
فاصله محل برخورد این خط روی محور افقی تا مبدا مختصات را x نامیده، همینطور فاصله این نقطه تا مبدا را روی محور عمودی y نامگذاری کردهایم. در دایره مثلثاتی، کسینوس زاویه را برابر با x و سینوس آن را y در نظر گرفته و تعریف میکنند. اگر از قضیه فیثاغورس به دنباله یک رابطه بین x و y در مثلث قائمالزاویه ساخته شده برگردیم، به تساوی زیر خواهیم رسید.
طرف راست تساوی بالا، همان مربع طول وتر مثلث قائمالزاویه یا شعاع دایره مثلثاتی است. حال x را با و y را با جایگزین میکنیم. به این ترتیب، مهمترین اتحاد مثلثاتی ساخته میشود.
پس اگر لازم باشد میتوان سینوس یک زاویه را برحسب کسینوس آن، یا برعکس بدست آورد. به رابطه زیر دقت کنید.
توجه داشته باشید حداکثر مقدار سینوس و کسینوس یک زاویه، با توجه به روابط بالا، هرگز بزرگتر از ۱ نخواهد بود. همچنین برای زاویه صفر درجه، مقدار کسینوس حداکثر یعنی ۱ بوده و برای زاویه ۹۰ درجه، مقدار کسینوس صفر است. برای سینوس این مقادیر برعکس هستند. یعنی برای زاویه صفر درجه، سینوس صفر و برای زاویه ۹۰ درجه، سینوس برابر با ۱ خواهد بود.
در تصویر زیر، موقعیت هر زاویه و همچنین علامت نسبتهای مثلثاتی سینوس و کسینوس را مشاهده و مقایسه کردهایم. بخشهای رنگی در تصویر زیر، ربعهای مثلثاتی هستند. قسمت صورتی رنگ (سمت راست بالا)، ربع اول، سبز رنگ (سمت چپ بالا)، ربع دوم، آبی کمرنگ (سمت چپ پایین)، ربع سوم و آبی پررنگ (سمت راست پایین)، ربع چهارم را تشکیل میدهند.
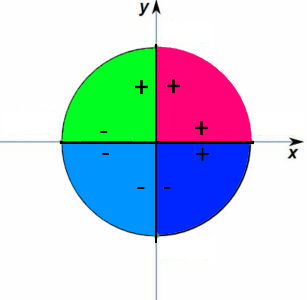
به این ترتیب مشخص است که یک دایره مثلثاتی، دارای چهار ربع یا بخش است. علامتهای + و - که در کنار محورهای سینوس و کسینوس در تصویر بالا دیده میشوند، نواحی مختلف با علامت هر یک از نسبتهای سینوس و کسینوس را مشخص کرده است. برای مثال، ناحیه اول که با رنگ صورتی مشخص شده، دارای مقدار مثبت برای هر دو نسبت مثلثاتی سینوس و کسینوس است. از طرفی ناحیه دوم یا سبز رنگ، دارای مقادیر سینوس مثبت ولی کسینوس منفی برای زاویههای این ناحیه است. در ناحیه آبی کمرنگ، برای همه زاویهها، هر دو نسبت مثلثاتی سینوس و کسینوس، منفی بوده ولی در قسمت آبی پرنگ، برای زوایا، سینوس منفی و کسینوس مثبت بوجود میآید.
دقت داشته باشید که علامت + و - که در کنار محور افقی (کسینوس) کشیده شده، علامت کسینوس و علامتهایی که در کنار محور عمودی (سینوس) قرار دارند، علامت سینوس را مشخص کردهاند. در ادامه مقدار سینوس زاویههای معروف و پر کاربرد را مشاهده میکنید.
نکته: جهت شمارهگذاری این بخشها در دایره مثلثاتی، پادساعتگرد یا برعکس حرکت عقربههای ساعت است. در بیشتر مواقع، جهت پادساعتگرد در ریاضیات برای توابع متناوب در نظر گرفته میشود. البته به راحتی میتوان جهت را برعکس در نظر گرفت و شبیه همان محاسبات را به کار برد.
تابع کسینوس به عنوان یک تابع تناوبی
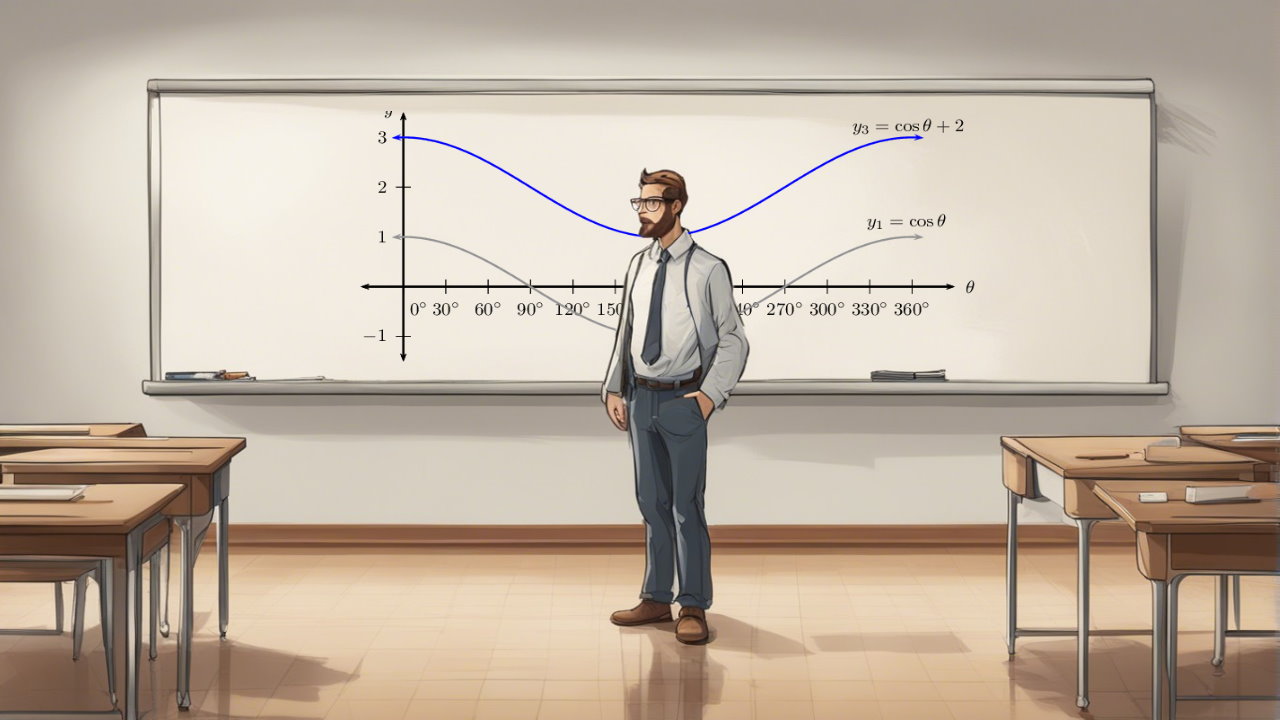
با توجه به تناوبی بودن تابع سینوس و کسینوس، میتوان یک نمودار برای آنها در مختصات دکارتی رسم کرده و متناسب با آن زاویه و نسبتهای مثلثاتی را روی دایره مثلثاتی مشاهده کرد. در تصویر زیر این کار صورت گرفته است.

با توجه به پویانمایی ارائه شده، تناوبی بودن تابع سینوس به خوبی نمایش داده شده.
همانطور که در تصویر متحرک پایین میبینید، تابع کسینوس با رنگ آبی ترسیم شده. در پایین آن نیز تابع سینوس با رنگ قرمز مشخص است.
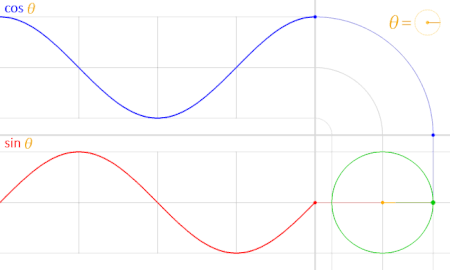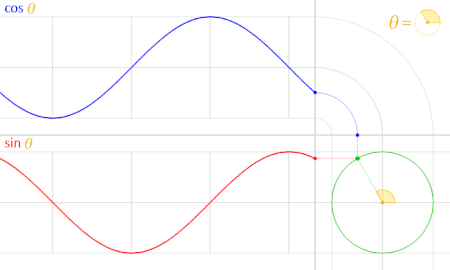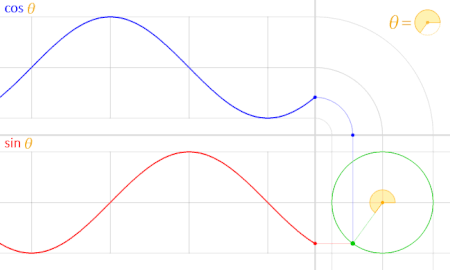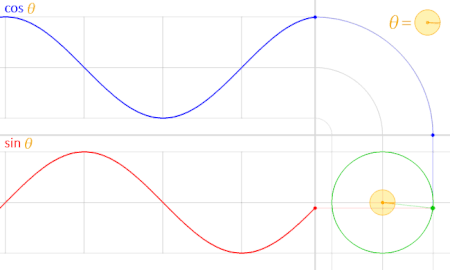
در تصویر بالا، دایره مثلثاتی در سمت راست، نیز با رنگ سبز مشخص شده و نقطهای که به رنگ سبز درون دایره چرخش دارد، زاویه را نشان میدهد. رنگ زرد نیز برای نمایش زاویه مورد نظر (با نماد ) به کار رفته و مقدار هر دو نسبت مثلثاتی سینوس و کسینوس در نمودار به صورت متناوب قابل مشاهدهاند. منظورمان از تناوب این است که اگر بیش از یک بار پیرامون دایره مثلثاتی بچرخیم، مقدار سینوس یا کسینوس زاویهها، تکرار شده و با هر بار گردش، به همان مقادیر قبلی خواهیم رسید.
با توجه به تصویر بالا، مشخص است که اختلاف فاز یا جابجایی زاویه برای نسبتهای مثلثاتی سینوس و کسینوس، ۹۰ درجه است. به این معنی که مقدار سینوس یک زاویه، با مقدار کسینوس آن زاویه بعلاوه ۹۰ درجه (یا همان ) برابر است. به تساویهای زیر توجه کنید.
همچنین برای سینوس نیز به همین شکل خواهیم داشت، البته باید به علامت سینوس و کسینوس در هر یک از ربعها نیز دقت داشت.
نکته: حرکت پاندول و آونگ، به عنوان یک حرکت متناوب شناخته شده که مکان هندسی محل آونگ برحسب توابع مثلثاتی مشخص میشود.
جدول مقدار کسینوس برای زاویههای پرکاربرد
در این قسمت میخواهیم مقدار سینوس و کسینوس زاویههای پرکاربرد را مشخص کنیم. همانطور که در تصویر زیر مشاهده میکنید زاویهها روی دایره مثلثاتی برحسب «عدد پی» () قابل مشاهدهاند. مختصاتی که روی محیط دایره ظاهر شدهاند، با دو مولفه قابل تشخیص هستند. مولفه اول که طول نقطه را نشان میدهد، همان مقدار کسینوس زاویه است و مولفه دوم نیز سینوس آن را تعیین میکند.

به یاد دارید که در مختصات دکارتی، هر نقطه در فضای دو بُعدی، با دو مولفه معرفی میشود. مولفه اول را طول و مولفه دوم را عرض آن نقطه مینامند. چنین حالتی را به صورت نشان میدهند. واضح است که طول و ، عرض نقطه است.
همانطور که در تصویر بالا میبینید، با افزایش مقدار زاویه در ربع اول، کسینوس کاهش یافته ولی سینوس افزایش مییابد. برای زاویه (یا همان ۹۰ درجه) به بعد یعنی ربع دوم، این وضعیت برعکس شده و سینوس کاهشی بوده و قدر مطلق کسینوس افزایشی میشود.
برای سادگی درک این موضوع، جدول سینوس کسینوس زیر را هم تهیه کردهایم که به مقایسه مقدار سینوس و کسینوس زاویههای مهم (برحسب درجه و رادیان) میپردازد. میدانید که درجه و رادیان و همچنین گراد، سه یکا برای اندازهگیری زاویه هستند. از طرفی باید بدانیم که مقدار سینوس یا کسینوس و هر نسبت مثلثاتی، از آنجایی که براساس تقسیم دو مقدار طول اضلاع ساخته میشود، بدون واحد است.
جدول مقایسه مقادیر سینوس و کسینوس زاویهها به همراه معکوس مقدار کسینوس (سکانت-sec)
| Radian | Degree | sin | cos | sec |
|---|---|---|---|---|
| 0 | 0° | |||
| π/12 | 15° | |||
| π/10 | 18° | |||
| π/8 | 22.5° | |||
| π/6 | 30° | |||
| π/5 | 36° | |||
| π/4 | 45° | |||
| 3π/10 | 54° | |||
| π/3 | 60° | |||
| 3π/8 | 67.5° | |||
| 2π/5 | 72° | |||
| 5π/12 | 75° | |||
| π/2 | 90° |
ستون آخر جدول بالا، به معکوس مقدار کسینوس زاویهها اشاره دارد که به آن سکانت (Sec) میگویند. مقایسه ستون چهارم و پنجم، این موضوع را به خوبی نشان میدهد. رابطه بین سینوس و کسینوس نیز در ستون سوم و چهارم قابل تحقیق است.
در ربع سوم یا (زاویه ۱۸۰ درجه) به بعد، باز هم قدر مطلق سینوس، افزایشی ولی قدر مطلق کسینوس کاهشی است. در زاویه (270 درجه) به بعد یا همان ربع چهار، قدر مطلق سینوس کاهشی ولی کسینوس افزایشی خواهد بود.
نکته: معکوس نسبت کسینوس را سکانت (Secant) و معکوس تابع سینوس را کسکانت (Cosecant) مینامند.
خلاصه و جمعبندی
سینوس و کسینوس که به عنوان توابع مثلثاتی پایه شناخته میشوند، موضوع اصلی این متن از مجله فرادرس میباشد. محاسبه نسبتهای مثلثاتی برحسب زاویههای مختلف طبق جدولهایی ارائه شد و خوانندگان با بعضی از اتحادهای مثلثاتی نیز آشنا شدند. مهم است که بدانید تعاریف اولیه برحسب نیاز ایجاد شدهاند تا بتوان به کمک آنها مسائل دنیایی واقعی را حل کرد. توابع مثلثاتی نیز از این قاعده مستثنی نیستند و به همین جهت، برای اندازهگیری و همچنین تعیین طول اضلاع شکلهای هندسی ابداع شدند. از طرفی کاربردهای وسیعی نیز در علوم مختلف بخصوص مهندسی مکانیک، عمران، برق و حتی فیزیک و شیمی دارند.
در این بین نمودار مقایسه سینوس و کسینوس را به عنوان توابع تناوبی در ریاضیات را مشخص و جدولی نیز برای نمایش کسینوس زاویههای مختلف ارائه کردیم. در نوشتارهای دیگر مجله فرادرس، مطلب زیادی در مورد توابع مثلثاتی پیدا خواهید کرد.













تابع مثلثات چرا با سینوس کسینوس شناخته میشوند؟
با سلام و عرض ادب
4 تا سوال از شما داشتم لطفا جواب بدید با سپاس فراوان:
اولیش اینکه ایا سایت شما تمام علم ریاضی-فیزیک-شیمی-زیست رو جمع کرده و اموزش داده یا اینکه ناقصه؟
دومیش اینکه با توجه به اینکه مطالب یک علم مثل ریاضی به هم پیوسته و ترکیبی هستش
من موندم که مقاله های ریاضی سایتتون رو به چه ترتیبی بخونم؟در مورد شیمی و فیزیک و زیست چطور؟
سومیش اینکه ایا سایت شما تو زمینه زمین شناسی اموزش داره ایا؟
و سوال اخرم اینکه من خیلی دوست دارم دانشمند بشم و موندم که چه رشته ای رو بخونم به نظر شما کدوم علم{شیمی-ریاضی-فیزیک-زیست-فیزیک فضا-فیزیک کوانتم و …} جذابه و تو دل برو هستش؟؟؟؟یکیشو بگید لطفا دلیلتون رو هم بگید
من میدونم که انتخاب بر اساس سلیقه و علاقه صورت میگیره ولی با این حال دوست دارم نظر شما رو هم بدونم 🙂
فیزیک کوانتوم بهترینشه چون به کشف و درک راز های هستی میپردازد
سلام، وقت شما بخیر؛
مجله فرادرس تا به امروز گستره وسیعی از مباحثی که شما سئوال کردید را پوشش داده است، در رابطه با ریاضیات میتوانید از فهرستی که در این پست تهیه و تدوین شده است استفاده کنید.