کسر مسلسل — به زبان ساده
تاریخچه کسرهای مسلسل به بیش از دو هزار سال قبل بر میگردد. یکی از اولین مطالعات در این زمینه، توسط اقلیدس و در حدود ۳۰۰ سال قبل از میلاد مسیح، در کتاب اصول هندسه اقلیدس ثبت شد. در آن هنگام، اقلیدس از کسر مسلسل برای یافتن بزرگترین مقسوم علیه مشترک دو عدد صحیح (آنچه امروز آن را الگوریتم اقلیدس مینامیم) استفاده کرد.
از آن زمان، کسرهای مسلسل (Continued Fractions) در موارد مختلفی مورد استفاده قرار گرفتهاند. برخی از این زمینهها، عبارتند از:
- تقریب گویای اعداد حقیقی
- حل معادلات دیوفانتین خطی
- حل معادله پِل
- تقریب عدد $$\pi$$
در ادامه، بیشتر درباره کسرهای مسلسل بحث خواهیم کرد.
انواع کسرهای مسلسل
دو نوع کسر مسلسل وجود دارد:
- کسر مسلسل متناهی (Finite Continued Fraction)
- کسر مسلسل نامتناهی (Infinite Continued Fraction)
یک کسر مسلسل متناهی نمایشی عمومی از عدد حقیقی $$ x $$ به فرم زیر است:
$$ \large
a _ { 0 } + \cfrac { b _ { 1 } } { a _ { 1 } + \cfrac { b _ { 2 } } { a _ 2 + \cfrac { b _ { 3 } } { a _ { 3 } + \cfrac { b _ { 4 } } { \ddots + \frac { b _ n } { a _ n } } } } } $$
که در آن، $$ a _ 0 $$، $$ a_ 1 $$ و... و $$b _ 1$$، $$ b _ 2 $$ و... اعدادی صحیح هستند و $$ n \ge 1 $$.
یک کسر مسلسل نامتناهی نمایشی عمومی از عدد صحیح $$ x $$ به فرم زیر است:
$$ \large a _ { 0 } + \cfrac { b _ { 1 } } { a _ { 1 } + \cfrac { b _ { 2 } } { a _ 2 + \cfrac { b _ { 3 } } { a _ { 3 } + \cfrac { b _ { 4 } } { a _ { 4 } + \ddots } } } } $$
که در آن، $$ a _ 0 $$، $$ a_ 1 $$ و... و $$b _ 1$$، $$ b _ 2 $$ و... اعدادی صحیح هستند.
یک نمایش کسر مسلسل نامتناهی از یک عدد حقیقی، به نوعی، مشابه با بسط عدد اعشاری آن است. به عنوان مثال، معادله $$\frac { 2 } { 11} = 0.181818...$$ به این معنی است که دنباله اعداد اعشاری $$ 0.1$$، $$0.18$$، $$0.181$$ و... به $$\frac { 2 }{11}$$ همگرا میشود. به طور مشابه، کسر مسلسل نامتناهیِ
$$ \large a _ { 0 } + \cfrac { b _ { 1 } } { a _ { 1 } + \cfrac { b _ { 2 } } { a _ 2 + \cfrac { b _ { 3 } } { a _ { 3 } + \cfrac { b _ { 4 } } { a _ { 4 } + \ddots } } } } $$
برابر با حد (درصورت وجود) دنباله کسرهای مسلسل بریده شده زیر است:
$$ \large a _ 0 , \ \ a _ 0 + \cfrac { b _ 1 } { a _ 1 } , \ \ a _ 0 + \cfrac { b _ 1 } { a _ 1 + \cfrac { b _ 2 } { a _ 2 } } , \ \ a _ 0 + \cfrac { b _ 1 } { a _ 1 + \cfrac { b _ 2 } { a _ 2 + \cfrac { b _ 3 } { a _ 3 } } } , \ \ \ldots . $$
وقتی $$ a _ i $$ و $$ b _ j $$ اعداد صحیحی باشند، این کسرهای مسلسل بریده، همه اعدادی گویا خواهند بود، دقیقاً همانطور که برابر با اعداد اعشاری بریده هستند.
کسرهای مسلسل ویژگیهای بسیار جالبی در ارتباط با تقریبهای گویا دارند که شامل کاربردهای مختفی از جمله حل معادله پل میشوند.
کسرهای مسلسل ساده و اعداد گویا
در بالا، کسرهای مسلسل با دو مجموعه عدد صحیح $$ a _ n $$ و $$ b _ n $$ تعریف شدند. حال اگر برای هر $$n$$، تساوی $$ b _ n = 1 $$ را قرار دهیم، این کسرها، کسر مسلسل ساده (Simple Continued Fraction) نامیده میشوند.
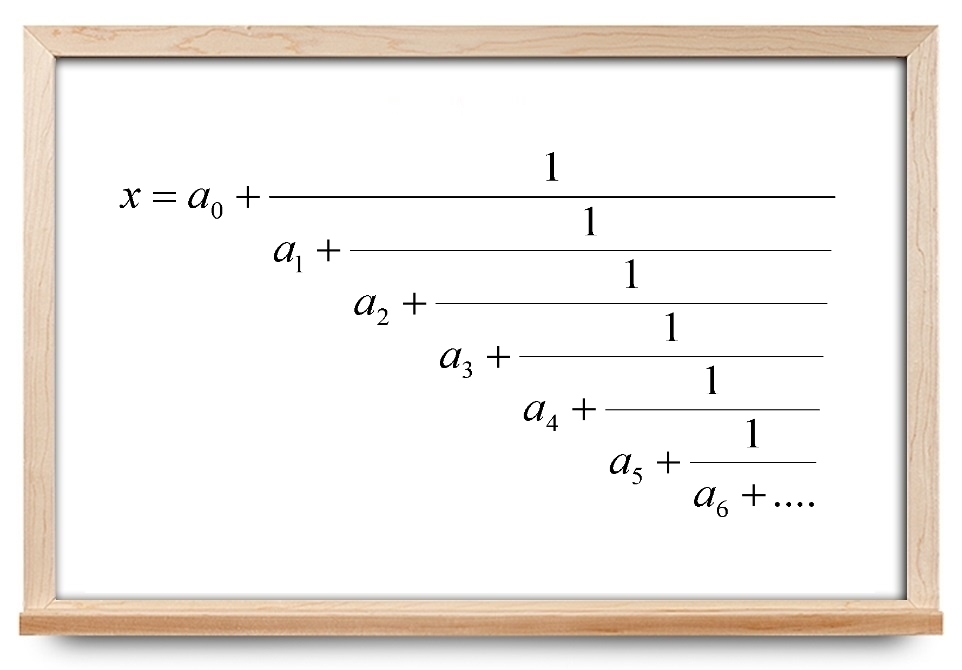
نمایش کسر مسلسل ساده نامتناهی عدد حقیقی $$ x $$ به فرم زیر است:
$$ \large a _ { 0 } + \frac { 1 } { a _ { 1 } + \frac { 1 } { a _ 2 + \frac { 1 } { a _ { 3 } + \ddots } } } $$
که در آن، $$ a _ 0 $$ یک عدد صحیح است و $$ a _ 1$$، $$ a _ 2$$ و... اعداد صحیح مثبتی هستند. کسر بالا اغلب به شکل فشردهتر زیر نوشته میشود:
$$ \large a _ { 0 } + \frac { 1 } { a _ { 1 } + } \frac { 1 } { a _ { 2 } + } \frac { 1 } { a _ { 3 } + } \cdots =[ a _ { 0 } ; a _ { 1 } , a _ { 2 } , a _ { 3 } , \ldots ] . $$
به طور مشابه، نمایش کسر مسلسل ساده متناهی عدد حقیقی $$ x $$ به فرم زیر است:
$$ \large a _ { 0 } + \frac { 1 } { a _ { 1 } + \frac { 1 } { a _ 2 + \frac { 1 } { \ddots + \frac { 1 } { a _ n } } } } $$
همانطور که در بالا گفتیم، کسر مسلسل ساده متناهی یک عدد گویا است. عکس این مطلب نیز صادق است. یعنی هر عدد گویای $$ \frac { m } { n } $$ را میتوان با استفاده از الگوریتم اقلیدس به یک کسر مسلسل ساده متناهی تبدیل کرد. این الگوریتم به صورت زیر بیان میشود:
اگر $$ m = n q + r $$ باشد، آنگاه $$\frac {m}{n} = q + \frac {r } { n } = q + \frac {1}{\frac{n}{r}} $$ و این فرایند با تقسیم $$n$$ بر $$ r $$ ادامه مییابد. مثال زیر، این فرایند را روش میکند.
مثال ۱
کسر $$ -\frac {551}{ 802}$$ را به یک کسر مسلسل ساده کاهش دهید.
حل: ابتدا الگوریتم اقلیدس را برای تقسیم $$ -551$$ بر $$802$$ مینویسیم:
$$ \large \begin {aligned} - 5 5 1 & = 8 0 2 ( - 1 ) + 2 5 1 \\ 8 0 2 & = 2 5 1 \cdot 3 + 4 9 \\ 2 5 1 & = 4 9 \cdot 5 + 6 \\ 4 9 & = 6 \cdot 8 + 1 \\ 6 & = 1 \cdot 6 + 0 . \end {aligned} $$
در نتیجه، خواهیم داشت:
$$ \large \begin {aligned} - \dfrac { 5 5 1 } { 8 0 2 } = - 1 + \dfrac { 2 5 1 } { 8 0 2 } & = - 1 + \dfrac { 1 } { \dfrac { 8 0 2 } { 2 5 1 } } \\\\ & = - 1 + \dfrac { 1 } { 3 + \dfrac { 4 9 } { 2 5 1 } } = - 1 + \dfrac { 1 } { 3 + \dfrac { 1 } { \dfrac { 2 5 1 } { 4 9 } } } \\\\ & = - 1 + \dfrac { 1 } { 3 + \dfrac { 1 } { 5 + \dfrac { 6 } { 4 9 } } } = - 1 + \dfrac { 1 }{ 3 + \dfrac { 1 } { 5 + \dfrac { 1 } { \dfrac { 4 9 } { 6 } } } } \\\\ & = - 1 + \dfrac { 1 } { 3 + \dfrac { 1 } { 5 + \dfrac { 1 }{ 8 + \dfrac { 1 } { 6 } } } } = - 1 + \dfrac { 1 } { 3 + } \dfrac { 1 } { 5 + } \dfrac { 1 } { 8 + } \dfrac { 1 } { 6 } . \end {aligned} $$
نتیجه نهایی محاسبات با نوشتن خارج قسمتهای الگوریتم اقلیدس به دست میآید:
$$ \large - \dfrac { 5 5 1 } { 8 0 2 } = [ - 1 ; 3 , 5 , 8 , 6 ] . \ _ \square $$
مثال ۲
در این مثال، کسر مسلسل متناوب را بررسی میکنیم. فرض کنید کسر زیر برابر با یک عدد حقیقی باشد. این عدد را پیدا کنید.
$$ \large 1 + \frac { 1 } { 1 + \frac { 1 } { 1 + \frac { 1 } { 1 + \ddots } } } = [ 1 ; 1 , 1 , 1 , \ldots ] $$
حل: ابتدا $$ k = [ 1 ; 1 , 1 , 1 , \ldots ] $$ را مینویسیم. در نتیجه، داریم:
$$ \large \begin {aligned} k & = 1 + \frac { 1 } { 1 + \frac { 1 }{ 1 + \frac { 1 } { 1 + \ddots } } } & \\ k & = 1 + \frac { 1 } { k } & \\ k ^ { 2 } - k - 1 & = 0 . \end {aligned} $$
بنابراین، $$ k = \dfrac { 1 \pm \sqrt { 5 } } 2 $$ است. اما از آنجایی که باید $$ k $$ بزرگتر از ۱ باشد، برابر با نسبت طلایی $$ \frac { 1 + \sqrt { 5 } } { 2 } $$ خواهد بود.
مثال ۳
حاصل کسر زیر را به دست آورید:
$$ \large 1 + \frac { 1 } { 1 + \frac { 1 } { 2 + \frac { 1 } { 1 + \frac { 1 } { 2 + \ddots } } } } = [ 1 ; 1 , 2 , 1 , 2 , \ldots ] . $$
حل: داریم:
$$ \large \begin {aligned} k & = 1 + \frac 1 { 1 + \frac 1 { 2 + ( k - 1 ) } } \\ k - 1 & = \frac { k + 1 } { k + 2 } \\ k ^ 2 + k - 2 & = k + 1 \\ k ^ 2 & = 3 \end {aligned} $$
بنابراین، $$ k = \sqrt { 3 } $$ (مثبت) جواب درست است.
مثال ۴
عدد $$ \sqrt { 7 } $$ را به صورت یک کسر مسلسل ساده بنویسید.
حل: برای به دست آوردن جواب، فرایند گرفتن بزرگترین عدد صحیح و متقابل آن را به صورت زیر مینویسیم و فرایند را تکرار میکنیم:
$$ \large \begin {aligned} \sqrt { 7 } & = 2 + ( \sqrt { 7 } - 2 ) \\ \frac 1 { \sqrt { 7 } - 2 } & = \frac { \sqrt { 7 } + 2 } 3 = 1 + \frac { \sqrt { 7 } - 1 } 3 \\ \frac 3 { \sqrt { 7 } - 1 } & = \frac { \sqrt { 7 } + 1 } 2 = 1 + \frac { \sqrt { 7 } - 1 } 2 \\ \frac 2 { \sqrt { 7 } - 1 } & = \frac { \sqrt { 7 } + 1 } 3 = 1 + \frac { \sqrt { 7 } - 2 } 3 \\ \frac 3 { \sqrt { 7 } - 2 } & = \sqrt { 7 } + 2 = 4 + ( \sqrt { 7 } - 2 ) \end {aligned} $$
این کار، منجر به کسر مسلسل زیر خواهد شد:
$$ \large \sqrt { 7 } = 2 + \frac 1 { 1 + \frac 1 { 1 + \frac 1 { 1 + \frac 1 { 4 + \ddots } } } } = [ 2 ; 1 , 1 , 1 , 4 , 1 , 1 , 1 , 4 , \ldots ] = \left [ 2 ; { \overline { 1 , 1 , 1 , 4 } } \right ] . \ _ \square $$
مثالهای اخیر منجر به قضیه زیر برای کسرهای مسلسل متناوب میشوند.
قضیه
فرض کنید $$ r$$ یک عدد حقیقی و $$ r = [ a _ 0 ; a _ 1 , a _ 2 , \ldots ] $$ یک کسر مسلسل ساده نامتناهی برای $$r$$ باشد که در آن، $$ a _ i $$ها اعدادی صحیح و $$a_1$$، $$a_2$$ و... اعداد مثبتی هستند. در نتیجه، دنباله $$ a _ i $$ متناوب است (یعنی عدد صحیح مثبت $$k$$ به گونهای وجود دارد که برای عدد به اندازه کافی بزرگ $$n$$، داشته باشیم: $$ a_ { n + k } = a _ n $$)، اگر و تنها اگر $$ r$$ ریشه یک چندجملهای درجه دوم با ضرایب صحیح باشد.
در این صورت، توصیف کاملی از اعداد حقیقی با استفاده از کسر مسلسل ساده متناوب خواهیم داشت. در حالت خاص $$ r = \sqrt { D} $$، این بسط ویژگیهای خاص و جالب دیگری نیز خواهد داشت که مرتبط با معادله پل $$ x ^ 2 - D y ^ 2 = 1 $$ است.
تقریب کسر گویا
در این بخش تعدادی از ویژگیهای عمومی مفید کسرهای مسلسل ساده را با تأکید بر تقریب کسر گویا بررسی میکنیم. در واقع، به این پرسش پاسخ خواهیم داد که «بهترین» تقریب یک عدد گنگ با یک عدد گویا چیست؟
قضیه
فرض کنید $$ r$$ یک عدد گویا بوده و دنباله اعداد صحیح یکتای $$ a _0$$، $$ a _ 1 $$، ... و $$ a _ k $$ و اعداد مثبت $$ a _ 1$$، $$ a _ 2$$ و ... و $$ a _ k \neq 1 $$ به گونهای وجود داشته باشند که $$ r = [ a _ 0 ; a _ 1 , \ldots , a _ k ] $$. این تساوی به این معنی است که دنباله کسرهای مسلسل بریده به $$r$$ میل میکند.
فرض کنید $$ P _ k $$ و $$ Q _ k $$ با فرمولهای بازگشتی زیر بیان شده باشند:
$$ \large \begin {aligned} P _ { - 1 } = 1 , \ P _ 0 = a _ 0 , \ P _ k & = a _ k P _ { k - 1 } + P _ { k - 2 } \quad ( k \ge 1 ) \\\\ Q _ { - 1 } = 0 , \ Q _ 0 = 1 , \ Q _ k & = a _ k Q _ { k - 1 } + Q _ { k - 2 } \quad ( k \ge 1 ) . \end {aligned} $$
در نتیجه، $$ \frac { P _ k } { Q _ k } $$ برابر با $$ k$$اُمین کسر مسلسل بریده $$ [ a _ 0 ; a _ 1 , \ldots , a _ k ] $$ خواهد بود.
کسرهای $$ \frac { P_ k } { Q _ k } $$ همگرا به عدد گنگ $$ r $$ نامیده میشوند.
مثال ۵
دنباله کسرهای همگرا به نسبت طلایی $$ \frac { 1 + \sqrt { 5 } } 2 $$ را به دست آورید.
حل: از آنجایی که کسر مسلسل به صورت $$ [ 1 ; 1 , 1 , \ldots ] $$ است، فرمول بازگشتی برابر با $$ P _ k = P_{k-1} + P _{ k - 2 } $$ بوده و فرمول مشابهی برای $$ Q _ k $$ خواهیم داشت. بنابراین، صورتها و مخرجها جملات متوالی دنباله فیبوناچی است:
$$ \large \left \{ \frac { P _ k } { Q _ k } \right \} _ { k = 0 } ^ { \infty } = \left \{ \frac 1 1 , \frac 2 1 , \frac 3 2 , \frac 5 3 , \frac 8 5 , \frac { 1 3 } 8 , \ldots \right \} . $$
قضیه اخیر بیان میکند که این کسرها به نسبت طلایی همگرا میشوند.
مثال ۶
کسر مسلسل عدد $$\pi$$ به صورت زیر شروع میشود:
$$ \large [ 3 ; 7 , 1 5 , 1 , 2 9 2 , \ldots ] . $$
چهار کسر اول همگرا به $$ \pi $$ را بیابید.
حل: با استفاده از فرمولها، به صورتها و مخرجهای زیر میرسیم:
$$ \large \frac 3 1 , \frac { 2 2 } 7 , \frac { 3 3 3 } { 1 0 6 } , \frac { 3 5 5 } { 1 1 3 } . $$
کسر آخر برابر با عدد زیر است و مشاهده میکنیم که تقریب مناسبی از عدد $$\pi$$ را ارائه میدهد:
$$ \large \frac { 3 5 5 } { 1 1 3 } = 3 . 1 4 1 5 9 2 9 2 \ldots . $$
خطای این تقریب کمتر از $$ \dfrac 1 { 1 0 0 0 0 0 0 } $$ است.
در ادامه، برخی ویژگیهای عمومی تقریب کسری همگرا را بیان میکنیم.
بهترین تقریب اعداد گویا با کسر مسلسل
در ارتباط با بهترین تقریب اعداد گویا با استفاده از کسر مسلسل، قضیه زیر را داریم.
قضیه
فرض کنید $$ r$$ یک عدد حقیقی گنگ و $$ \frac { P_k}{Q_k}$$ کسرهای همگرای آن باشند. در نتیجه، داریم:
- $$ \frac { P _ k }{ Q _ k } $$ و $$ \frac { P_{k+1}} { Q _ {k+1}}$$ در دو طرف $$ r $$ قرار دارند؛ بدین معنی که در سمت چپ و راست $$r$$ روی محور اعداد هستند.
- $$ \left | \frac { P _ { k + 1 } } { Q _ { k + 1 } } - r \right | < \left | \frac { P _ k } { Q _ k } - r \right | $$
- $$ \left | \frac { P _ { k + 1 } } { Q _ { k + 1 } } - \frac { P _ k } { Q _ k } \right | = \frac 1 { Q _ k Q _ { k + 1 } } $$. توجه کنید که سمت چپ این تساوی دقیقاً برابر با مجموع دو مقدار نامعادله قبل است.
- از هر زوج متوالی همگرا، یعنی $$\frac {P_k}{Q_k}$$ و $$\frac {P_{k+1}}{Q_{k + 1 }}$$، حداقل یکی در نامعادله $$ \left | \frac { P } { Q } - r \right | < \dfrac 1 { 2 Q ^ 2 } $$ صدق میکند (توجه کنید که نامعادله قبلی بیان میکند که هر دو در $$ \left | \frac { P } { Q } - \alpha \right | < \frac 1 { Q ^ 2 } $$ صدق میکنند).
- اگر $$ \left | \frac { P } { Q } - r \right | < \frac 1 { 2 Q ^ 2 } $$، آنگاه $$\frac { P } { Q} $$ باید یک کسر همگرا باشد.
- اگر $$ \left | \frac { P } { Q } - r \right | < \left | \frac { P _ k } { Q _ k } - r \right | $$، آنگاه $$ Q > Q _ k $$. بدین معنی که کسرهای همگرا «بهترین» تقریبهای $$ r$$ هستند. یعنی هیچ عدد گویای دیگری با مخرج کوچکتر نمیتواند به $$r$$ نزدیکتر شود (توجه کنید که همه بهترین تقریبها همگرا نیستند، اما همه کسرهای همگرا بهترین تقریبها هستند).
- اگر $$ \frac { P}{Q}$$ به گونهای باشد که $$ | P- Q r |$$ برای هر $$Q'<Q$$ کوچکتر از $$| P' -Q' r |$$ شود، آنگاه $$\frac { P } { Q} $$ باید یک کسر همگرا باشد. همچنین، به طور عکس، همه کسرهای همگرا دارای این ویژگی هستند. (بنابراین، در این مفهوم جایگزین از بهترین تقریب، کسرهای همگرا دقیقاً بهترین تقریبها هستند).
این قضیه تصویری جامع از ماهیت ویژه کسرهای همگرا و استفاده از آنها در تقریب مناسب اعداد حقیقی ارائه میدهد.
یکی از کابردهای عمومی کسرهای مسلسل تقریب ریشه دوم اعداد با استفاده از رابطه زیر است:
$$ \large \sqrt { n } = 1 + \frac { n - 1 } { 2 + \frac { n - 1 }{ 2 + \frac { n - 1 } { 2 + \ddots } } } . $$
مثال ۷
رابطه زیر را اثبات کنید.
$$ \large \sqrt { n } = 1 + \frac { n - 1 } { 2 + \frac { n - 1 }{ 2 + \frac { n - 1 } { 2 + \ddots } } } . $$
حل: ابتدا تساوی زیر را در نظر بگیرید:
$$ \large \sqrt { n } + n = \sqrt { n } + n + 1 - 1 . $$
با فاکتورگیری از سمت چپ رابطه بالا، داریم:
$$ \large \sqrt { n } ( 1 + \sqrt { n } ) = 1 + \sqrt { n } + n - 1 . $$
حال، دو طرف رابطه اخیر را بر $$ 1 + \sqrt { n } $$ تقسیم میکنیم:
$$ \large \sqrt { n } = 1 + \frac { n - 1 } { 1 + \sqrt { n } } . $$
در نهایت، مقدار $$ \sqrt { n} $$ را جایگذاری کرده و به رابطه زیر میرسیم:
$$ \large \sqrt { n } = 1 + \frac { n - 1 } { 2 + \frac { n - 1 } { 2 + \ddots } } $$
این فرایند را میتوان تا بینهایت ادامه داد.
مثال ۸
دنباله تقریبهای گویای عدد $$\sqrt 5$$ را به دست آورید.
حل: با توجه به مثال قبل، داریم:
$$ \large \sqrt { 5 } = 1 + \frac 4 { 2 + \frac 4 { 2 + \frac 4 { 2 + \ddots } } } $$
دنباله کسرهای مسلسل بریده شده به صورت زیر هستند:
$$ \large 1 , \ \ 1 + \frac 4 2 ,\ \ 1 + \frac 4 { 2 + \frac 4 2 } , \ \ 1 + \frac 4 { 2 + \frac 4 { 2 + \frac 4 2 } } , \ \ \ldots $$
در نتیجه، دنباله کسرهای همگرا به فرم زیر خواهند بود:
$$ \large 1 , \ 3 , \ 2 , \ \frac 7 3 , \ \ldots $$
که به $$\sqrt 5 $$ میل میکند.
کسر مسلسل در متلب
در این بخش، کدهای مربوط به پیادهسازی کسر مسلسل در متلب را ارائه میکنیم.
برنامه زیر محاسبه تقریب کسر مسلسل یک عدد را نتیجه میدهد. این کد بدین صورت عمل میکند که برای مقدار $$R$$، $$N$$ جمله کسر مسلسل را تعیین میکند که تقریبی از عدد $$R$$ است.
1function [ p, q ] = i4cf_evaluate ( n, a, b )
2
3%*****************************************************************************80
4%
5%% I4CF_EVALUATE evaluates a continued fraction with I4 entries.
6%
7% Discussion:
8%
9% For convenience, we omit the parentheses or multiline display.
10%
11% CF = A(0) + B(1) / A(1) + B(2) / A(2) + ... A(N-1) + B(N) / A(N).
12%
13% Licensing:
14%
15% I don't care what you do with this code.
16%
17% Modified:
18%
19% 05 August 2017
20%
21% Author:
22%
23% John Burkardt
24%
25% Reference:
26%
27% John Hart, Ward Cheney, Charles Lawson, Hans Maehly, Charles Mesztenyi,
28% John Rice, Henry Thatcher, Christoph Witzgall,
29% Computer Approximations,
30% Wiley, 1968.
31%
32% Parameters:
33%
34% Input, integer N, the number of continued fraction
35% coefficients.
36%
37% Input, integer A(N+1), B(N+1), the continued fraction
38% coefficients. The first entry of B is ignored.
39%
40% Output, integer P(N+1), Q(N+1), the N+1 successive approximations
41% to the value of the continued fraction.
42%
43 p = zeros ( 1, n + 1 );
44 q = zeros ( 1, n + 1 );
45
46 for i = 0 : n
47
48 if ( i == 0 )
49 p(i+1) = a(i+1) * 1 + 0;
50 q(i+1) = a(i+1) * 0 + 1;
51 elseif ( i == 1 )
52 p(i+1) = a(i+1) * p(i) + b(i+1) * 1;
53 q(i+1) = a(i+1) * q(i) + b(i+1) * 0;
54 else
55 p(i+1) = a(i+1) * p(i) + b(i+1) * p(i-1);
56 q(i+1) = a(i+1) * q(i) + b(i+1) * q(i-1);
57 end
58
59 end
60
61 return
62endبرنامه مربوط به کسر مسلسل ساده نیز به صورت زیر است.
1function [ p, q ] = i4scf_evaluate ( n, a )
2
3%*****************************************************************************80
4%
5%% I4SCF_EVALUATE evaluates a simple continued fraction with I4 entries.
6%
7% Discussion:
8%
9% The simple continued fraction with integer coefficients is:
10%
11% SCF = A(0) + 1 / ( A(1) + 1 / ( A(2) ... + 1 / A(N) ) )
12%
13% This routine returns the successive approximants P(I)/Q(I)
14% to the value of the rational number represented by the continued
15% fraction, with the value exactly equal to the final ratio P(N)/Q(N).
16%
17% Licensing:
18%
19% I don't care what you do with this code.
20%
21% Modified:
22%
23% 04 August 2017
24%
25% Author:
26%
27% John Burkardt
28%
29% Reference:
30%
31% John Hart, Ward Cheney, Charles Lawson, Hans Maehly, Charles Mesztenyi,
32% John Rice, Henry Thatcher, Christoph Witzgall,
33% Computer Approximations,
34% Wiley, 1968.
35%
36% Parameters:
37%
38% Input, integer N, the number of continued fraction
39% coefficients.
40%
41% Input, integer A(0:N), the continued fraction coefficients.
42%
43% Output, integer P(0:N), Q(0:N), the numerators and
44% denominators of the successive approximations.
45%
46 p = zeros ( 1, n + 1 );
47 q = zeros ( 1, n + 1 );
48
49 for i = 0 : n
50
51 if ( i == 0 )
52 p(i+1) = a(i+1) * 1 + 0;
53 q(i+1) = a(i+1) * 0 + 1;
54 elseif ( i == 1 )
55 p(i+1) = a(i+1) * p(i) + 1;
56 q(i+1) = a(i+1) * q(i) + 0;
57 else
58 p(i+1) = a(i+1) * p(i) + p(i-1);
59 q(i+1) = a(i+1) * q(i) + q(i-1);
60 end
61
62 end
63
64 return
65endکد زیر نیز نتایج حاصل از اجرای برنامه را در خروجی چاپ میکند.
1function i4vec_print ( n, a, title )
2
3%*****************************************************************************80
4%
5%% I4VEC_PRINT prints an I4VEC.
6%
7% Licensing:
8%
9% This code is distributed under the GNU LGPL license.
10%
11% Modified:
12%
13% 25 January 2004
14%
15% Author:
16%
17% John Burkardt
18%
19% Parameters:
20%
21% Input, integer N, the dimension of the vector.
22%
23% Input, integer A(N), the vector to be printed.
24%
25% Input, string TITLE, a title.
26%
27 if ( 0 < length ( title ) )
28 fprintf ( 1, '\n' );
29 fprintf ( 1, '%s\n', title );
30 end
31 fprintf ( 1, '\n' );
32
33 for i = 1 : n
34 fprintf ( 1, '%6d: %6d\n', i, a(i) );
35 end
36
37 return
38endکدهای پایتون محاسبه کسر مسلسل
کدهای مربوط به محاسبه کسر مسلسل در پایتون را میتوانید از اینجا [+] دانلود کنید.
کدهای C محاسبه کسر مسلسل
کدهای مربوط به محاسبه کسر مسلسل در زبان برنامهنویسی سی در اینجا [+] قابل دریافت است.
کدهای C++ محاسبه کسر مسلسل
کدهای مربوط به محاسبه کسر مسلسل در سی پلاس پلاس را میتوانید از اینجا [+] دانلود کنید.
اگر این مطلب برای شما مفید بوده است، آموزشها و مطالب زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس ریاضیات
- آموزش جامع ریاضی دبیرستان – ریاضی و فیزیک
- مجموعه آموزشهای دروس دبیرستان و پیشدانشگاهی
- آموزش ریاضیات عمومی 1
- ک م م یا کوچکترین مضرب مشترک چیست؟ — به زبان ساده
- قواعد بخش پذیری یا عاد کردن — به زبان ساده
- تعداد رقم های عدد توان دار — به زبان ساده
^^











واقعا عالی بود … تشکر
اکر ممکن هست لطفا کسرهای مسلسل رامانوجان رو اضافه کنید .