تعداد رقم های عدد توان دار — به زبان ساده
از عنوان این نوشتار تعجب کردهاید؟ حتما خواهید گفت که تعداد رقم های عدد توان دار را به روش شمارش ارقامش به راحتی میتوان بدست آورد. البته گفته شما کاملا صحیح است ولی شاید در بعضی از موارد شمارش ارقام کاری مشکل بوده یا حتی توان رساندن عدد بسیار سخت باشد. در این نوشتار با استفاده از تقسیمهای متوالی بر ۱۰ و همچنین تابع لگاریتم و آنچه به عنوان خصوصیات آن میشناسیم، پاسخ مناسبی به این مسئله خواهیم داد.
برای آشنایی با نحوه به توان رساندن اعداد توان دار — به زبان ساده و نماد علمی — به زبان ساده را مطالعه کنید. همچنین خواندن ویژگیهای تابع لگاریتم در نوشتار لگاریتم و خصوصیات آن — به زبان ساده نیز برایتان جذابیت خواهد داشت. از طرفی خواندن نوشتارهای ویژگی های تابع نمایی — به زبان ساده و لگاریتم و هر آنچه باید درباره آن بدانید – به زبان ساده نیز خالی از لطف نیست.
تعداد رقم های عدد توان دار
فرض کنید از شما پرسیده شود، عدد $$3^5$$ چند رقم است؟ از آنجایی که به راحتی و بدون ماشین حساب میتوان عدد ۳ را به توان ۵ رساند، تعداد رقمهای آن نیز به سادگی شمرده میشود.
$$\large 3^5 = 3 \times 3 \times 3 \times 3 \times 3 = 243$$
پس تعداد رقم های این عدد توان دار برابر با ۳ است. هر چند این کار در اینجا به راحتی انجام شد ولی ممکن است توان رساندن تبدیل به امری بسیار دشوار شود.
برای مثال برای تعیین تعداد ارقام عدد $$4^{16}$$، توان رساندن به وسیله ضرب کردن به سختی صورت میگیرد و بهتر است از ماشین حساب استفاده کنیم.
$$\large 4^{16} =4,294,967,296$$

به هر حال مشخص میشود که این عدد شامل ۱۰ رقم است. ولی این بار در نظر بگیرد که عددی که به دنبال تعداد رقمهای آن هستید، به شکل باورنکردنی بزرگ است. به نظر شما عدد $$159^{256}$$ چند رقم دارد؟ اگر این محاسبه را به کمک ماشین حساب انجام دهیم به نتیجه زیر خواهیم رسید. همانطور که میبینید برای نمایش این عدد از نماد علمی استفاده شده است.
$$\large 159^{256}=3.6113021465e563$$
با توجه به توانهای به کار رفته در نمایش نماد علمی مشخص میشود که این عدد، شامل 564 رقم خواهد بود.
نکته: گاهی برای نمایش اعداد بسیار بزرگ یا بسیار کوچک، از «نماد علمی» (Scientific Notation) استفاده میشود. به این ترتیب تعداد ارقام یک عدد را میتوان یکی بیشتر از مقدار توان یا نمای $$e$$ در نظر گرفت. همانطور که قبلاً مشاهده کردید، عدد 3.6113021465e563 دارای 563+1=564 رقم خواهد بود.
این بار باز هم عدد را بزرگتر میکنیم تا حتی ماشین حساب هم با توجه به محدودیتی که در محاسبات دارد، قادر نباشد نتیجه توان رساندن را بدست آورد. به نظر شما تعداد ارقام عدد $$123456789^{123456}$$ چقدر است؟ در چنین حالتی، نه تنها ماشین حساب، بلکه رایانهها نیز از بدست آوردن حاصل توان، عاجز میشوند. نتیجه محاسبه این عدد در اکسل به شکل زیر خواهد بود:
$$\large 123456789^{123456} =\#NUM! $$
همانطور که میبینید، اکسل قادر به نمایش یا محاسبه این عدد نیست. پس چگونه میتوانیم تعداد ارقام عدد حاصل از این محاسبه را بدست آوریم؟ در ادامه به کمک تقسیم و لگاریتم به پاسخ مناسبی برای این سوال خواهیم رسید. نکته جالب در این موضوع آن است که بدون محاسبه و بدست آوردن حاصل عملیات به توان رساندن، میتوانیم دقیقا بگوییم که عدد حاصل چند رقم خواهد داشت.
تعیین تعداد رقم های عدد به کمک تقسیم
میدانیم که هر عدد طبیعی (مثل $$a$$) را میتوان به صورت مجموعی از توانهای ۱۰ و به شکل زیر نوشت، بطوری که $$a_0, a_1,\ldots, a_k$$ همگی اعداد طبیعی کوچکتر از ۱۰ هستند.
$$\large a = a_0\times 10^0 + a_1\times 10^1+ a_2\times 10^2+\ldots+ a_k\times 10^k$$
رابطه ۱
از این موضوع میتوان متوجه شد که $$k+1$$ نشانگر تعداد ارقام عدد $$a$$ است زیرا همه جملههای رابطه بالا که قبل از $$a_k\times 10^k$$ قرار دارند از آن کوچکتر بوده و مجموع آنها هرگز بزرگتر از $$a_k\times a^k$$ نخواهد بود. به بیان ریاضی این ویژگیها به صورت زیر نوشته میشوند:
$$\large a_0\times 10^0 < a_1\times 10^1< a_2\times 10^2<\ldots< a_k\times 10^k$$
$$\large a_0\times 10^0 + a_1\times 10^1+ a_2\times 10^2+\ldots+ a_{k-1}\times 10^{k-1}<a_k\times 10^k$$
در نتیجه هر بار که عدد $$a$$ را بر ۱۰ تقسیم میکنیم، یکی از رقمهای آن را مشخص کردهایم. جدول زیر به بررسی مراحل تقسیم و استخراج رقم به رقم از عدد $$a$$ پرداخته است.
| تعداد مراحل تقسیم | تقسیم (مقسوم و مقسوم علیه) | خارج قسمت | رقم استخراج شده (باقیمانده) |
| 1 | $$\large \dfrac{a_0\times 10^0 +\ldots+ a_{k-1}\times 10^{(k-1)}+a_k\times 10^k}{10}$$ | $$\large a_1+ \ldots+ a_{k}\times 10^{(k-1)}$$ | $$\large a_0$$ |
| 2 | $$\large \dfrac{a_1+ \ldots+ a_k\times 10^{(k-1)}}{10}$$ | $$\large a_2+\ldots+ a_{k}\times 10^{(k-2)}$$ | $$\large a_1$$ |
| 3 | $$\large \dfrac{a_2+\ldots+ a_k\times 10^{(k-2)}}{10}$$ | $$\large a_3+\ldots+ a_{k}\times 10^{(k-3)}$$ | $$\large a_2$$ |
| $$\ldots$$ | $$\ldots$$ | $$\ldots$$ | $$\ldots$$ |
| $$k$$ | $$\large \dfrac{a_{k}\times 10^{k-(k-1)}}{10}$$ | $$\large a_k$$ | $$\large a_{k-1}$$ |
| $$k+1$$ | $$\large \dfrac{a_{k}}{10}$$ | $$<1$$ | $$\large a_{k}$$ |
برای مثال، 234 را میتوان به صورت زیر و برمبنای حاصل ضرب عبارتهایی از توانهای ۱۰ نوشت:
$$\large 234 = 4 \times 10^0+ 3 \times 10^1+ 2 \times 10^2$$
در نتیجه مطابق با جدول بالا، ارقام آن را یک به یک استخراج میکنیم. واضح است که تعداد مراحل تقسیم، میتواند الگویی برای پیدا کردن تعداد ارقام عدد باشد.
| تعداد مراحل تقسیم | تقسیم (مقسوم و مقسوم علیه) | خارج قسمت | رقم استخراج شده (باقیمانده) |
| 1 | $$\large \dfrac{4\times 10^0 + 3\times 10^1+ 2\times 10^2}{10}$$ | $$\large 3+ 2\times 10^1$$ | $$\large 4$$ |
| 2 | $$\large \dfrac{3+ 2\times 10^1}{10}$$ | $$\large 2\times 10$$ | $$\large 3$$ |
| 3 | $$\large \dfrac{ 2\times 10}{10}$$ | $$\large 2$$ | $$\large 2$$ |
پس تعداد ارقام این عدد برابر است با 3. بنابراین اگر تابع $$N(a)$$ را به شکلی در نظر بگیریم که تعداد ارقام $$a$$ را مشخص میکند، خواهیم داشت:
$$\large N(234) = (2+1)=3$$
کدهای برنامهنویسی برای پیدا کردن تعداد رقم های عدد
در ادامه به کدهایی اشاره میکنیم که به کمک آنها قادر هستیم تعداد ارقام یک عدد را بوسیله تقسیم متوالی آن بر ۱۰ محاسبه کنیم. در اینجا فرض شده است که با ورود دو عدد $$a$$ و $$b$$، حاصلضرب آن دو محاسبه شده و تعداد ارقام حاصلضرب مشخص شود. ممکن است $$a$$ یا $$b$$ مثبت یا منفی باشند در نتیجه به کمک تابع قدر مطلق (abs) ابتدا مقدار حاصلضرب را بدون علامت کرده سپس تعداد ارقام را میشماریم.
البته در ادامه به شیوهای اشاره میکنیم که حتی بدون ضرب کردن این دو عدد نیز میتوانیم تعداد ارقام حاصلضرب را بدست آوریم.
برنامه پیدا کردن تعداد رقم های عدد در ++C
1// C++ implementation to count number of digits
2// in the product of two numbers
3#include <bits/stdc++.h>
4
5using namespace std;
6
7// function to count number of digits
8// in the product of two numbers
9int countDigits(int a, int b)
10{
11 int count = 0;
12
13 // absolute value of the
14 // product of two numbers
15 int p = abs(a*b);
16
17 // if product is 0
18 if (p == 0)
19 return 1;
20
21 // count number of digits in the product 'p'
22 while (p > 0)
23 {
24 count++;
25 p = p / 10;
26 }
27
28 // required count of digits
29 return count;
30}
31
32// Driver program to test above
33int main()
34{
35 int a = 33;
36 int b = -24;
37 cout << "Number of digits = "
38 << countDigits(a,b);
39 return 0;
40} برنامه پیدا کردن تعداد رقم های عدد در جاوا
1// Java implementation to count
2// number of digits in the product
3// of two numbers
4import java.io.*;
5import java.math.*;
6
7class GFG {
8
9 // function to count number of digits
10 // in the product of two numbers
11 static int countDigits(int a, int b)
12 {
13 int count = 0;
14
15 // absolute value of the
16 // product of two numbers
17 int p = Math.abs(a * b);
18
19 // if product is 0
20 if (p == 0)
21 return 1;
22
23 // count number of digits in
24 // the product 'p'
25 while (p > 0)
26 {
27 count++;
28 p = p / 10;
29 }
30
31 // required count of digits
32 return count;
33 }
34
35 // Driver program to test above
36 public static void main(String args[])
37 {
38 int a = 33;
39 int b = -24;
40 System.out.println("Number of digits = "
41 + countDigits(a, b));
42 }
43}
44
45/*This code is contributed by Nikita Tiwari.*/برنامه پیدا کردن تعداد رقم های عدد در پایتون
1# Python 3 implementation to count
2# number of digits in the product
3# of two numbers
4
5# function to count number of digits
6# in the product of two numbers
7def countDigits(a, b) :
8 count = 0
9
10 # absolute value of the
11 # product of two numbers
12 p = abs(a * b)
13
14 # if product is 0
15 if (p == 0) :
16 return 1
17
18 # count number of digits
19 # in the product 'p'
20 while (p > 0) :
21 count = count + 1
22 p = p // 10
23
24
25 # required count of digits
26 return count
27
28
29# Driver program to test above
30a = 33
31b = -24
32print("Number of digits = ",
33 countDigits(a,b))
34
35# This code is contributed by Nikita Tiwari. برنامه پیدا کردن تعداد رقم های عدد در #C
1// C# implementation to count
2// number of digits in the product
3// of two numbers
4using System;
5
6class GFG {
7
8 // function to count number of digits
9 // in the product of two numbers
10 static int countDigits(int a, int b)
11 {
12 int count = 0;
13
14 // absolute value of the
15 // product of two numbers
16 int p = Math.Abs(a * b);
17
18 // if product is 0
19 if (p == 0)
20 return 1;
21
22 // count number of digits in
23 // the product 'p'
24 while (p > 0) {
25 count++;
26 p = p / 10;
27 }
28
29 // required count of digits
30 return count;
31 }
32
33 // Driver program to test above
34 public static void Main()
35 {
36 int a = 33;
37 int b = -24;
38 Console.WriteLine("Number of digits = " +
39 countDigits(a, b));
40 }
41}
42
43// This code is contributed by Sam007 برنامه پیدا کردن تعداد رقم های عدد در PHP
1<?php
2// PHP implementation to count
3// number of digits in the
4// product of two numbers
5
6// function to count number
7// of digits in the product
8// of two numbers
9function countDigits($a, $b)
10{
11 $count = 0;
12
13 // absolute value of the
14 // product of two numbers
15 $p = abs($a * $b);
16
17 // if product is 0
18 if ($p == 0)
19 return 1;
20
21 // count number of digits
22 // in the product 'p'
23 while ($p > 0)
24 {
25 $count++;
26 $p = (int)($p / 10);
27 }
28
29 // required count of digits
30 return $count;
31}
32
33// Driver Code
34$a = 33;
35$b = -24;
36echo "Number of digits = " .
37 countDigits($a, $b);
38
39// This code is contributed by mits
40?> تعیین تعداد رقم های عدد به کمک لگاریتم
همانطور که در قسمت قبل دیدید، از آنجایی که میتوانیم هر عدد طبیعی را به فرم رابطه ۱ و برمبنای ۱۰ بنویسیم، برای محاسبه تعداد ارقام یک عدد از تقسیمهای متوالی آن بر عدد ۱۰ استفاده میکنیم. از طرفی با توجه به مفهوم لگاریتم نیز میتوانیم تعداد مراحل تقسیم یک عدد بر ۱۰، را بدست آوریم.
برای مثال، فرض کنید میخواهیم بدانیم در ۱۰۰ چند دسته ۱۰تایی وجود دارد. این امر دقیقا مانند عمل تقسیم است که بطور متوالی صورت میگیرد.
$$\large \log_{10} 100 =2$$
بنابراین میدانیم که تعداد ارقام ۱۰۰ برابر است با 3=2+1. به این ترتیب میتوانیم فرمول کلی محاسبه تعداد ارقام را بدست آوریم. پس اگر باز هم $$N$$ را تابع محاسبه تعداد ارقام در نظر بگیریم، خواهیم داشت:
$$\large N(a) = [\log_{10}(a)]+1$$
رابطه ۲
همانطور که میدانید، علامت $$[ \;\;] $$ را براکت یا جزء صحیح عدد در نظر میگیرند. به تابع جز صحیح گاهی تابع کف (Floor) نیز میگویند.
مثال 1
برای پیدا کردن تعداد ارقام عدد ۹۸۷۶۵۴۳۲۱ نیز از لگاریتم برمبنای ۱۰ استفاده میکنیم. در این صورت باید محاسبه کنیم که تعداد تقسیمهای متوالی آن بر ۱۰ چند است. همانطور که گفتیم این کار را به کمک لگاریتمگیری انجام میدهیم.
$$\large \log_{10} 987654321 = 8.99460$$
اگر حاصل را به پایین گرد کنیم یا جز صحیح را محاسبه کنیم و حاصل را با ۱ جمع کنیم، تعداد ارقام عدد مورد نظر استخراج میشود.
$$\large N(987654321) = [\log_{10}(987654321)]+1 = 8+1 = 9$$
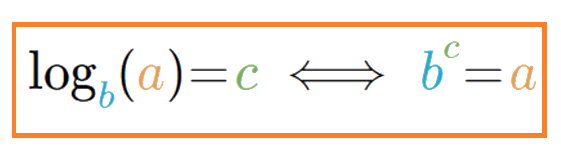
نکته: اگر بخواهیم تعداد ارقام عدد $$a$$ را برمبنای ۲ محاسبه کنیم، باید لگاریتم را هم برمبنای ۲ بدست آوریم. پس در حالت کلی تعداد ارقام عدد $$a$$ برمبنای $$b$$ به صورت زیر نوشته میشود.
$$\large N_b(a) = [\log_b(a)]+1$$
مثال ۲
تعداد رقمهای عدد 256 اگر برمبنای ۲ نوشته شود به صورت زیر استخراج میشود.
$$\large N_2(256) = [\log_2(256)]+1=8+1=9$$
مشخص است که ۲۵۶ برمبنای ۲ به صورت 100000000 نوشته میشود که دارای ۹ رقم است. همچنین اگر بخواهیم تعداد ارقام ۲۵۶ را برمبنای ۸ محاسبه کنیم، میتوانیم بنویسیم:
$$\large N_8(256) = [\log_8(256)]+1=[2.66]+1=3$$
مشخص است که عدد ۲۵۶ برمبنای ۸ به صورت 100 نوشته میشود که دارای سه رقم است.
پیدا کردن تقریبی مقدار لگاریتم عدد
همانطور که در رابطه ۲ مشاهده کردید، لگاریتم و جزء صحیح برای محاسبه تعداد ارقام یک عدد به کار گرفته شد. حال اگر این عبارت را برعکس کنیم، میتوانیم مقدار تقریبی لگاریتم یک عدد را محاسبه کنیم. کافی است که تعداد ارقام یک عدد را مشخص کرده و یک واحد از آن کم کنیم. در این صورت مقدار تقریبی لگاریتم بدست خواهد آمد.
$$\large N(a) = [\log_{10}(a)]+1 \rightarrow \log(a)\approx N(a)-1$$
رابطه ۳
مثال ۳
برطبق مثال ۱ مشخص شد که لگاریتم عدد 987654321 برابر است با 8٫99460، حال سعی میکنیم به کمک رابطه ۳، مقدار تقریبی لگاریتم 987654321 را محاسبه کنیم.
$$\large \log_{10}(a)\approx N(a)-1 \rightarrow \log_{10}(987654321) \approx 9-1=8$$
بنابراین مقدار لگاریتم این عدد تقریبا ۸ خواهد بود. البته روشهایی برای تعیین ارقام اعشار مقدار لگاریتم نیز وجود دارد که در مطلبی مجزا در مجله فرادرس به آنها خواهیم پرداخت.
تعداد ارقام حاصلضرب دو عدد
همانطور که مشاهده کردید، تعداد ارقام برای یک عدد را براساس تعداد مراحل تقسیم آن بر ۱۰ یا لگاریتم آن بدست آوردیم. حال به بررسی تعداد ارقام حاصلضرب دو عدد میپردازیم. به این ترتیب اگر $$m$$ و $$n$$ دو عدد طبیعی باشند، میخواهیم بدانیم حاصل $$m\times n$$ چند رقم دارد. همانطور که قبلا اشاره کردیم، یک راه حل میتواند محاسبه حاصل ضرب و لگاریتمگیری باشد. ولی از آنجایی که لگاریتم ضرب دو عدد تبدیل به مجموع لگاریتم آنها میشود، خواهیم داشت:
$$\large N_{10}(m \times n) = [\log_{10} (m \times n)]+1 = [\log_{10} m + \log_{10} n ]+1$$
بنابراین بدون آنکه عمل ضرب را انجام دهیم میتوانیم تعداد ارقام حاصلضرب را بدست آوریم. کافی است که لگاریتم هر یک از آن اعداد را برمبنای ۱۰ محاسبه کرده و با یکدیگر جمع کنیم. سپس به جزء صحیح مجموع آنها مقدار ۱ را اضافه کنیم.
مثال ۴
تعداد ارقام حاصل ضرب ۱۲۳۴۵ در ۶۷۸۹ به صورت زیر محاسبه میشود.
$$\large N_{10}(12345 \times 6789) = [\log_{10}(12345) + \log_{10}(6789) ]+1 $$
$$\large = [4.09149+3.8318] + 1 = 7+1 = 8$$
از آنجایی که این حاصلضرب برابر است با $$83810205$$ به خوبی کارایی فرمول ارائه شده مشخص میشود.
مثال ۵
در این مثال تعداد ارقام حاصلضرب 123456789987654321 در 987654321123456789 را بدست میآوریم.
$$\large N_{10}(123456789987654321 \times 987654321123456789) $$
$$\large =[\log_{10}(123456789987654321) + \log_{10}(987654321123456789) ]+1 $$
$$\large =[17+17]+1 = 34+1 = 35$$
تعیین تعداد رقم های عدد توان دار با لگاریتم
فرض کنید $$m$$ و $$p$$ دو عدد از مجموعه اعداد طبیعی (به غیر از صفر) باشند. با توجه به خصوصیات لگاریتم برای این دو عدد میتوان نوشت:
$$\large \log_{10}m^p= p \log_{10} m$$
از همین خاصیت برای پیدا کردن تعداد ارقام عدد توان دار استفاده میکنیم. البته از آنجایی که توان را به صورت توالی عمل ضرب نیز میتوان در نظر گرفت، رابطه قبلی که در مورد تعداد ارقام حاصل ضرب دو عدد گفته شد، قابل استفاده است.
$$\large N(k)= N(m^p)= [\log_{10}(m^p)]+1 = [p \times \log_{10}(m)]+1$$
مثال ۶
تعداد ارقام عدد $$123456789^{123456}$$ برابر است با:
$$\large N(123456789^{123456})$$
$$ \large =[123456 \times \log_{10}(123456789)]+1$$
$$ \large = (123456 \times [8.09151])+1=998946+1 = 998947$$
کدهای برنامهنویسی برای پیدا کردن تعداد رقم های عدد توان دار
در ادامه کدهایی را به زبانهای مختلف برنامهنویسی مشاهده میکنید که محاسبات مربوط به تعداد رقم های عدد توان دار را انجام میدهند. فرض شده است که مقدارهای ورودی به صورت $$a=2$$ و $$b=100$$ هستند و قرار است تعداد ارقام $$a^b$$ محاسبه شود.
برنامه پیدا کردن تعداد رقم های عدد توان دار در ++C
1// CPP Program to calculate
2// no. of digits in a^b
3#include<iostream>
4#include<math.h>
5using namespace std;
6
7// function to calculate number
8// of digits in a^b
9int no_of_digit(int a, int b)
10{
11 return ((int)(b * log10(a)) + 1);
12}
13
14// driver program
15int main()
16{
17 int a = 2, b = 100;
18 cout <<"no. of digits = "<<
19 no_of_digit(a, b);
20}
21
22// This code is contributed by Smitha برنامه پیدا کردن تعداد رقم های عدد توان دار در جاوا
1// Java Program to calculate
2// no. of digits in a^b
3class GFG {
4
5 // function to calculate number
6 // of digits in a^b
7 static int no_of_digit(int a, int b)
8 {
9 return ((int)(b * Math.log10(a)) + 1);
10 }
11
12 // driver program
13 public static void main(String[] args)
14 {
15 int a = 2, b = 100;
16 System.out.print("no. of digits = " +
17 no_of_digit(a, b));
18 }
19} برنامه پیدا کردن تعداد رقم های عدد توان دار در پایتون
1# Python Program to calculate
2# no. of digits in a^b
3import math
4
5# function to calculate number
6# of digits in a^b
7def no_of_digit(a, b):
8 return ((int)(b * math.log10(a)) + 1)
9
10# Driver Program
11a = 2
12b = 100
13print("no of digits = ", no_of_digit(a, b))
14
15# This code is contributed by Shrikant13 برنامه پیدا کردن تعداد رقم های عدد توان دار در #C
1# Python Program to calculate
2# no. of digits in a^b
3import math
4
5# function to calculate number
6# of digits in a^b
7def no_of_digit(a, b):
8 return ((int)(b * math.log10(a)) + 1)
9
10# Driver Program
11a = 2
12b = 100
13print("no of digits = ", no_of_digit(a, b))
14
15# This code is contributed by Shrikant13 برنامه پیدا کردن تعداد رقم های عدد توان دار در PHP
1<?php
2// PHP Program to calculate
3// no. of digits in a^b
4
5// function to calculate number
6// of digits in a^b
7function no_of_digit($a, $b)
8{
9 return ((int)($b * log10($a)) + 1);
10}
11
12// Driver Code
13$a = 2; $b = 100;
14echo("no. of digits = " .no_of_digit($a, $b));
15
16// This code is contributed by Ajit.
17?> خلاصه و جمعبندی
در این نوشتار با نحوه محاسبه تعداد ارقام عدد، ضرب دو عدد و عدد توان دار با استفاده از لگاریتم و خصوصیات آن آشنا شدیم. همچنین به کمک برنامههایی به زبانهای مختلف نظیر پایتون، ++C، جاوا، #C و PHP، این محاسبات را انجام دادیم. همانطور که دیدید، بدون آنکه لازم باشد حاصل عمل توان رساندن را انجام دهیم، میتوانیم تعداد ارقام یک عدد تواندار را محاسبه کنیم. این امر میتواند برای ارزیابی خطاهای محاسباتی مورد استفاده قرار گیرد.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس ریاضیات
- آموزش ریاضی عمومی ۱ (همراه با حل مثال و تست کنکور کارشناسی ارشد)
- مجموعه آموزشهای ریاضی و فیزیک
- لگاریتم و خصوصیات آن — به زبان ساده
- قواعد بخش پذیری یا عاد کردن — به زبان ساده
- تقسیم عدد صحیح — به زبان ساده
^^











منظور من اذ پرسش سؤال در خصوص فيزيك كوانتم است كه كوچكترين ذره را به زبان رياضى با چه عددى مى توان نمايش داد؟