ب م م یا بزرگترین مقسوم علیه مشترک چیست؟ — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

در آموزشهای قبلی از مجموعه مطالب ریاضی مجله فرادرس، درباره تجزیه اعداد به عوامل اول بحث کردیم. همچنین با مفهوم و نحوه محاسبه کوچکترین مضرب مشترک یا ک م م آشنا شدیم. در این آموزش از مجله فرادرس، مفهوم «بزرگترین مقسوم علیه مشترک» (Greatest Common Divisor) یا ب م م یا GCD و نحوه به دست آوردن آن را بررسی میکنیم.
مقسوم علیه یا عامل چیست؟
مقسومٌ علَیه یا عامل، در ریاضیات به معنای عددی است که عددی دیگر بر آن تقسیم شده است.
به عبارت دیگر، عاملها اعدادی هستند که میتوان آنها را در یکدیگر ضرب کرد و عدد دیگری را به دست آورد. برای مثال، عاملهای عدد ۶ به صورت زیر هستند:
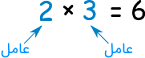
هر عدد، مقسوم علیههای مختلفی دارد. برای مثال، مقسوم علیههای عدد ۱۲، اعداد 1، 2، 3، 4، 6 و 12 هستند. زیرا:
۶ × 2 = 12 یا 3 × ۴ = 12 یا ۱۲ × ۱ = 12
بزرگترین مقسوم علیه مشترک چیست؟
مقسوم علیههای مشترک چند عدد، مقسوم علیهها یا عواملی هستند که در هر دو عدد مشترک باشند.
بزرگترین مقسوم علیه مشترک نیز، همان گونه که از نامش پیداست، بزرگترین عدد بین مقسوم علیههای مشترک دو عدد است.
مثال ۱
برای مثال، مقسوم علیههای دو عدد 12 و 30 را میتوان به صورت زیر فهرست کرد:
- مقسوم علیههای ۱۲: 1، 2، 3، 4، 6 و 12.
- مقسوم علیههای 30: 1، 2، 3، 5، 6، 10، 15 و 30.
همانطور که میبینیم، اعداد 1، 2، 3 و 6 در فهرست مقسوم علیههای هر دو عدد وجود دارند. بنابراین، مقسوم علیههای مشترک 12 و 30، اعداد 1، 2، 3 و 6 هستند. بزرگترین این اعداد، عدد ۶ است.
مثال ۲
یک مثال دیگر را برای سه عدد بررسی میکنیم. سه عدد 15، 30 و 105 را در نظر بگیرید.میخواهیم مقسوم علیههای مشترک آنها را به دست آوریم.
- مقسوم علیههای عدد 15: 1، 3، 5 و 15.
- مقسوم علیههای عدد 30: 1، 2، 3، 5، 6، 10، 15 و 30.
- مقسوم علیههای عدد 105: 1، 3، 5، 7، 15، 21، 35 و 105.
همانطور که میبینیم، مقسوم علیههای مشترک، اعداد 1، 3، 5 و 15 هستند و بزرگترین آن ها ۱۵ است.
کاربرد مقسوم علیه مشترک چیست؟
اگر به مثال قبل دقت کنیم، میبینیم که بزرگترین مقسوم علیه مشترک اعداد 15، 30 و 105، عدد 15 است. اما کاربرد این عدد چیست؟ یکی از مهمترین کاربردهای بزرگترین مقسومعلیه مشترک، ساده کردن کسر است.
برای مثال، کسر $$ \frac{12}{30} $$ را در نظر بگیرید. چگونه میتوانیم این کسر را ساده کنیم؟ قبلاً مقسوم علیههای دو عدد 12 و 30 را بهدست آوردیم که اعداد 1، 2، 3 و ۶ بودند و گفتیم که بزرگترین مقسوم علیه مشترک دو عدد، 6 است.
بنابراین، بزرگترین عددی که میتوانیم هر دو عدد 12 و 30 را بر آن تقسیم کنیم، 6 خواهد بود:
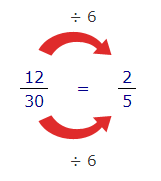
همانطور که میبینیم، کسر $$ \frac {12} {30}$$ به کسر $$\frac {2}{5}$$ ساده میشود.
محاسبه بزرگترین مقسومعلیه مشترک
برای محاسبه ب م م دو راه وجود دارد.
روش اول
- همه مقسوم علیههای دو عدد مورد نظر را به دست میآوریم.
- پس از آن، مقسوم علیههای مشترک را انتخاب میکنیم.
- در نهایت بزرگترین مقسوم علیه مشترک را تعیین میکنیم.
با یک مثال شروع میکنیم. میخواهیم بزرگترین مقسوم علیه مشترک دو عدد ۱۲ و ۱۶ را بنویسیم.
ابتدا عوامل یا همان مقسومعلیههای هر عدد را به دست میآوریم. پس از آن، دور عوامل مشترک یک دایره میکشیم. در نهایت، از بین عوامل مشخص شده، بزرگترین را انتخاب میکنیم.
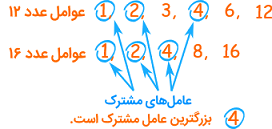
جداول زیر، مثالهایی از این روش را برای اعداد ۹ و ۱۲ و نیز اعداد ۶ و ۱۶ نشان میدهد.
| دو عدد | مقسوم علیهها | مقسوم علیههای مشترک | بزرگترین مقسوم علیه مشترک | مثال سادهسازی کسر |
| 9 و 12 | 9: 1، 3، 9
12: 1، 2، 3، 4، 6، 12 | 1، 3 | 3 | $$ \frac {9} {12} = \frac {3} {4} $$ |
| دو عدد | مقسوم علیهها | مقسوم علیههای مشترک | بزرگترین مقسوم علیه مشترک | مثال سادهسازی کسر |
| 6 و 18 | 6: 1، 2، 3، 6
18: 1، 2، 3، 6، 9، 18 | 1، 2، 3، 6 | 6 | $$ \frac {6} {18} = \frac {1} {3} $$ |
روش دوم
میتوانیم اعداد را به عوامل اول تجزیه کرده و مشترکات آنها را با هم ترکیب کنیم. جدول زیر، استفاده از این روش را نشان میدهد.
| دو عدد | تجزیه به عوامل اول | ب.م.م. | مثال سادهسازی کسر |
| 24 و 108 | $$ 2 \times 2 \times 2 \times 3 = 24 $$
$$ 2 \times 2 \times 3 \times 3 \times 3 = 108 $$ | $$ 2 \times 2 \times 3 = 12 $$ | $$ \frac {24}{108} = \frac {2}{9} $$ |
آزمون سنجش یادگیری ب م م
در این بخش از مجله فرادرس، سطح اطلاعات شما در مبحث ب م م را با طرح سوالهای چندگزینهای میسنجیم. پس از جواب دادن به تمام سوالها، نتیجه آزمون برای شما به نمایش درمیآید.
ب م م اعداد 6 و 15 چیست؟
2
3
6
15
برای به دست آوردن بزرگترین مقسومعلیه مشترک بین دو عدد، مقسومعلیههای کامل آنها مینویسیم:
- مقسومعلیههای 6: 1، 2، 3، 6
- مقسومعلیههای 15: 1، 3، 5، 15
- مقسومعلیههای مشترک 6 و 15: 1، 3
بین مقسومعلیههای اعداد 6 و 15، دو عدد 1 و 3 مشترک هستند. به این ترتیب، بزرگترین مقسومعلیه مشترک 6 و 15 برابر با 3 است.
بزرگترین مقسوم علیه مشترک اعداد 45 و 105 چیست؟
15
25
35
45
برای به دست آوردن بزرگترین مقسومعلیه مشترک اعداد 45 و 105، مقسومعلیههای کامل آنها مینویسیم:
- مقسومعلیههای 45: 1، 3، 5، 9، 15، 45
- مقسومعلیههای 105: 1، 3، 5، 7، 15، 21، 35، 105
- مقسومعلیههای مشترک 45 و 105: 1، 3، 5، 15
با توجه به اعداد بالا، بزرگترین مقسوم علیه مشترک اعداد 45 و 105 برابر با 15 است.
کدامیک از گزینههای زیر، ب م م اعداد 180، 225 و 270 را نمایش میدهد؟
15
30
45
90
برای به دست آوردن بزرگترین مقسومعلیه مشترک اعداد 180، 225 و 270، مقسومعلیههای کامل آنها مینویسیم:
- مقسومعلیههای 180: 1، 2، 3، 4، 5، 6، 9، 10، 12، 15، 18، 20، 30، 36، 45، 60، 90، 180
- مقسومعلیههای 225: 1، 3، 5، 9، 15، 25، 45، 75، 225
- مقسومعلیههای 270: 1، 2، 3، 5، 6، 9، 10، 15، 18، 27، 30، 45، 54، 90، 135، 270
- مقسومعلیههای مشترک 180، 225 و 270: 1، 3، 5، 9، 15، 45
با توجه به اعداد بالا، بزرگترین مقسوم علیه مشترک اعداد 180، 225 و 270 برابر با 45 است.
ب م م اعداد 72 و 252 چیست؟
12
18
24
36
برای به دست آوردن بزرگترین مقسومعلیه مشترک اعداد 72 و 252، مقسومعلیههای کامل آنها مینویسیم:
- مقسومعلیههای 72: 1، 2، 3، 4، 6، 8، 9، 12، 18، 24، 36، 72
- مقسومعلیههای 252: 1، 2، 3، 4، 6، 7، 9، 12، 14، 18، 21، 28، 36، 42، 63، 84، 126، 252
- مقسومعلیههای مشترک 72 و 252: 1، 2، 3، 4، 6، 9، 12، 18، 36
با توجه به اعداد بالا، بزرگترین مقسوم علیه مشترک اعداد 72 و 252 برابر با 36 است.
بزرگترین مقسومعلیه مشترک اعداد 126 و 196، کدام گزینه است؟
28
21
18
14
برای به دست آوردن بزرگترین مقسومعلیه مشترک اعداد 126 و 196، مقسومعلیههای کامل آنها مینویسیم:
- مقسومعلیههای 126: 1، 2، 3، 6، 7، 9، 14، 18، 21، 42، 63، 126
- مقسومعلیههای 196: 1، 2، 4، 7، 14، 28، 49، 98، 196
- مقسومعلیههای مشترک 126 و 196: 1، 2، 7، 14
با توجه به اعداد بالا، بزرگترین مقسوم علیه مشترک اعداد 126 و 196 برابر با 14 است.











سلام خسته نباشید لطفا میشه بهم بگید ب.م.م عدد (25.30) میشه چند آخه هر دفعه یه عدد به دست میاد مثلا من به این اعداد رسیدم: 5،10،25 الان نمیدنم کدوم درسته خواهشا راهنمایی کنید.
میشه ۵
5 میشه عزیزم
ب م م یک عدد منفی و یک عدد مثبت چی میشه
ب م م یک عدد فرد و یک عدد مثبت چی میشه
سلام خسته نباشید من به یک مشکلی برخوردم و اینکه روش اول و روش دوم متفاوت است یا به یک جواب میرسیم من ب.م.م عدد 32 و 38 رو به روش اول حل کردم اما به روش دوم جور دیگه ای محاسبه میشه آیا بزرگ ترین مقسوم علیه برای اعداد که قابله ضرب هستند استفاده میشه ؟
اگه نشد تجزیه کنیم چی؟
خسته نباشید
روش دیگری برای بدست آوردن ب م م وجود نداره ،
سلام ب.م.م دو عدد ۱۸_۲۷چیه؟؟
خسته نباشید ….سفره تون پربرکت
سلام.
خوشحالیم که این آموزش برایتان مفید بوده است.
شاد و پیروز باشید.
سلام.
مطالق آنچه در متن آموزش گفتهایم، عوامل دو عدد را مینویسیم:
۱۸: ۲ و ۳ و ۳
۲۷: ۳ و ۳ و ۳
میبینیم که ۳ و ۳ مقسومعلیههای مشترک هستند. بنابراین، ب.م.م. این دو عدد $$3\times 3 = 9 $$ است.
موفق باشید.
عالی
خیلی عالی ممنون
سلام و سپاس از همراهیتان با مجله فرادرس.
شاد باشید.
اگه بینشون عامل مشترک نداشت چی؟؟؟؟
ب م م دو عدد که بینشون عامل مشترک وجود نداشته باشه(نسبت به هم اول باشند) برابر با یک است
عالی بود من تو ب م م اشکال داشتم ولی با دیدن ویدیو خیلی خوب و دقیق یاد گرفتم ممنون از شما .
ممنون
عالی بود
تعبير هندسی ب م م و ک م م چی میشه
ممنون از شما
خیلی عالی بود. ممنون از شما
سلام.
خوشحالیم که این آموزش برایتان مفید بوده است.
سالم و موفق باشید.
عالی بوددایول❤❤❤❤❤
دستتون درد نکنه من واقعا از روی کتاب نفهمیدم ولی با توصیحات شما عالی یاد گرفتم و فردا امتحان داشتم
عالییییییییییییی بود واقعااا دستتون درد نکن به بهترین روش ممکن درس دادین.
بزرگ ترین ب م م 300تا 700
ب.م.م۸۰و۹۰چقدر میشه
خیلیییییییی خوب بود من از همین نوشته ها فهمیدم ولی حال ندارم فیلمارو ببینم ??
سلام.
خوشحالیم که این آموزش به یادگیریتان کمک کرده است.
سالم و شاد باشید.
میشه10دیگ
خوب بود مرسی;-)
سلام باتشکر از اساتید محترم که این قدر با آرامش وبازبانی ساده توضیح میدن که دانش آموز خیلی راحت مفهوم رودرک میکنه خدا قوت به تمامی اساتید فرادرس
عااااااااااااااااااااااااااااااااااااااااااااااااااااااااالیه
عالی بود دم همه ی اساتید فرادرس گرم که اینقد پر انرژی هستند.من برای یادگیری ریاضی و انگلیسی از این سایت استفاده میکنم و باز می گم دمتون گرم
الهی که خدا حفظت کنه کیف می کنم گوش میکنم صداتو با اون موسیقی بسیااااار شاد و پر امید که بکراند توتریالات هست، کاشکی معلم ها، اساتید و مدرسان مثل خودت باشن
ای کاش از راه نمودار درختی هم حل میکردید?
اره
آره من که متوجه نشدم راه حل هاش چی بود
عالی خیلی ب دردم خورد ازتون سپاسگذارم?
عالی،ممنون.
دمتون گرم من هیچی بلد نبودم عاللللللللللللللللللللللللی بود مطلب هاتون خیلی خوب اموزش میدین با تشکر از شما
بخدا ب م م و ک م م رو بلد نبودم ولی با مطالب شما دقیق یاد گرفتم عالـــــــــــــــــــــــــــــی بود
منم خوشم آمد