مکانیک تحلیلی چیست؟ – به زبان ساده + معرفی منابع یادگیری

مکانیک تحلیلی یکی از دروس تخصصی اصلی در رشته فیزیک است که در این مطلب سعی داریم تا بعد از معرفی اصول اولیه مکانیک تحلیلی به معرفی منابع چاپی و ویدیویی معتبر و برتر این درس بپردازیم. اگر شما به تازگی با مفاهیم این موضوع آشنا شده‌اید پیشنهاد می‌کنیم تا خواندن این مطلب را از دست ندهید.

مکانیک چیست؟

مکانیک علم مربوط به حرکت اجسام تحت تأثیر نیروها و مورد خاصی که در آن جسمی در حالت سکون باقی می‌ماند، است. اولین چالش در مسئله حرکت، نیروهایی است که اجسام بر یکدیگر اعمال می‌کنند.

این امر به مطالعه موضوعاتی مانند گرانش، الکتریسیته و مغناطیس با توجه به ماهیت نیروهای درگیر منجر می‌شود. با توجه به نیروها، می‌توان نحوه حرکت اجسام تحت تأثیر نیروها را بررسی کرد. این موضوع مربوط به مکانیک است.

از نظر تاریخی، مکانیک یکی از اولین علوم دقیق بود که توسعه یافت. زیبایی درونی آن به عنوان یک رشته ریاضی و موفقیت چشمگیر اولیه آن در محاسبات جزئیات کمی برای حرکت‌های ماه، زمین و دیگر اجرام سیاره‌ای تأثیر به سزایی بر اندیشه فلسفی داشت و انگیزه‌ای برای توسعه سیستماتیک علم ایجاد کرد.

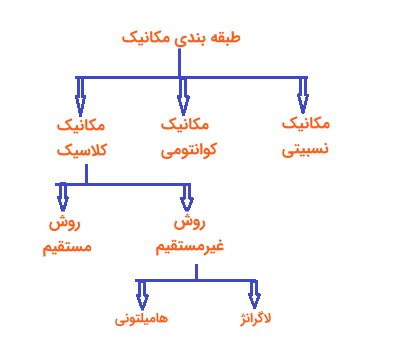
مکانیک را می‌توان به سه شاخه تقسیم کرد: استاتیک، که به بررسی نیروهای وارد بر جسم و در حالت سکون می‌پردازد. سینماتیک، که حرکات احتمالی جسم یا سیستم اجسام را توصیف می‌کند و سینتیک، که تلاش دارد تا حرکتی را که در یک موقعیت معین رخ می‌دهد را توضیح دهد و یا پیش بینی کند. از طرف دیگر مکانیک‌ها را می‌توان با توجه به نوع سیستم مورد مطالعه تقسیم بندی کرد. ساده ترین سیستم مکانیکی، ذره است که به عنوان جسمی بسیار کوچک تعریف شده است که شکل و ساختار داخلی آن، در مسئله داده شده هیچ تاثیری ندارد. پیچیده‌تر از این سیستم حرکت یک سیستم با دو یا چند ذره است که بر یکدیگر نیرو وارد می‌کنند و احتمالاً تحت نیروهایی خارج از سیستم نیز قرار می‌گیرند.

اصول مکانیک در سه حوزه کلی برای پدیده‌ها اعمال می‌شود. با استفاده از این علم می‌توان حرکت اجرام آسمانی مانند ستارگان، سیارات و ماهواره‌ها را هزاران سال قبل از وقوع با دقت بالایی پیش‌بینی کرد. البته نظریه نسبیت برخی انحرافات حرکت بر اساس مکانیک کلاسیک یا نیوتنی را پیش بینی می‌کند. با این حال این تاثیرات آن قدر کوچک‌اند که تنها با تکنیک‌های بسیار دقیق قابل مشاهده هستند، مگر در مسائلی که شامل تمام یا بخش بزرگی از جهان قابل مشاهده باشد.

سیستم دوم مکانیکی، اجسام معمولی روی زمین تا اندازه میکروسکوپی هستند که با سرعت بسیار کمتر از سرعت نور حرکت می‌کنند. این سیستم‌ها توسط مکانیک کلاسیک و بدون اصلاحات قابل توجه توصیف می‌شوند. مهندسی که پل یا هواپیما طراحی می‌کند، با اطمینان از قوانین نیوتنی مکانیک کلاسیک استفاده می‌کند، حتی اگر نیروها بسیار پیچیده بوده و محاسبات فاقد سادگی زیبای مکانیک سماوی باشند. سومین حوزه مکانیک شامل رفتار ماده و تابش الکترومغناطیسی در مقیاس اتمی و زیر اتمی است. اگرچه موفقیت‌های اولیه محدودی در توصیف رفتار اتم‌ها از نظر مکانیک کلاسیک وجود داشت، اما این پدیده‌ها در مکانیک کوانتومی به درستی بررسی می‌شوند.

مکانیک کلاسیک با حرکت اجسام تحت تأثیر نیروها یا تعادل اجسام زمانی که همه اجسام در حال تعادل هستند، سروکار دارد. این موضوع برای اولین بار توسط اسحاق نیوتن در کتاب Philosophiae Naturalis Principia Mathematica (1687) که معمولاً به Principia معروف است، بیان شد. این مفروضات را به نام قوانین حرکت نیوتن، در مکانیک می‌شناسیم. این قوانین برای پیش بینی دقیق انواع مختلف پدیده‌ها از جمله حرکت ذرات منفرد تا فعل و انفعالات سیستم‌های بسیار پیچیده استفاده می‌شوند. انواع مختلفی از کاربردهای قوانین نیوتن در مطالب مختلف مجله فرادرس توضیح داده شده است.

در چارچوب فیزیک مدرن، مکانیک کلاسیک را می توان تقریبی دانست که از قوانین عمیق‌تر و دقیق‌تر مکانیک کوانتومی و نظریه نسبیت ناشی می‌شود. با این حال فیزیک مدرن و دانشمندان این علم، نقش و اهمیت فیزیک کلاسیک در شکل‌گیری و تبیین فیزیک مدرن را بسیار کم اهمیت و ناچیز توصیف می‌کنند. دیدگاه امروزی ما از جهان و جایگاه انسان در آن ریشه در مکانیک کلاسیک دارد. علاوه بر این بسیاری از نظریات و نتایج مکانیک کلاسیک هنوز به عنوان اصول درست علمی در نظر گرفته می‌شوند و نقش مهمی در فیزیک جدید ایفا می‌کنند.

مفاهیم اصلی در مکانیک کلاسیک عبارت از نیرو، جرم و حرکت است. نه نيرو و نه جرم به خوبی توسط نيوتن تعريف نشده‌اند و هر دو از زمان نيوتن موضوع حدس و گمان‌های فلسفی زيادی بوده‌اند. هر دوی این مفاهیم با تأثیراتشان بیشتر شناخته می‌شوند. جرم اندازه گیری گرایش جسم به مقاومت در برابر تغییرات حالت حرکت است. از طرف دیگر نیروها به اجسام شتاب می‌دهند، یعنی حالت حرکت اجسامی را که به آنها نیرو اعمال می‌شود تغییر می‌دهند. تأثیر متقابل این جلوه‌ها موضوع اصلی مکانیک کلاسیک است.

اگرچه قوانین نیوتن بر نیرو و جرم تمرکز می‌کنند، اما سه کمیت دیگر نیز اهمیت ویژه‌ای دارند زیرا مقدار کل آن‌ها هرگز تغییر نمی‌کند. این سه مقدار انرژی، تکانه (خطی) و تکانه زاویه ای هستند. هر یک از این موارد را می‌توان از یک جسم یا سیستم به جسم دیگر منتقل کرد. علاوه بر این ممکن است انرژی در حالی که با یک سیستم واحد مرتبط است، تغییر شکل دهد و به صورت انرژی جنبشی (انرژی حرکتی جسم و سیستم)، انرژی پتانسیل (انرژی موقعیت و گرما) یا انرژی داخلی (انرژی مربوط به حرکت‌های تصادفی اتم‌ها یا مولکول‌هایی که هر جسم واقعی را تشکیل می‌دهند) یا ترکیبی از این سه انرژی با این شرط که مقدار کل انرژی، تکانه خطی و تکانه زاویه‌ای در جهان هرگز تغییر نمی‌کند. این قانون در فیزیک با این بیان تبیین می‌شود که مقدار کل انرژی، تکانه خطی و تکانه زاویه‌ای در عالم پایسته است. این سه قانون بقا از قوانین نیوتن نشأت می‌گیرد اما خود نیوتن آن‌ها را بیان نکرده است و بعدها از اصول مکانیک کلاسیک بیان شد.

این یک واقعیت قابل توجه است که اگر چه قوانین نیوتن دیگر اصل تلقی نمی‌شوند و حتی دقیقاً صحیح نیستند، اما سه قانون پایستگی مشتق شده از قوانین نیوتن یعنی پایستگی انرژی، تکانه خطی و تکانه زاویه ای حتی در مکانیک کوانتومی نیز کاملاً صادق است. این در حالی است که در نسبیت و در واقع در فیزیک مدرن، نیرو دیگر یک مفهوم اصلی نیست و جرم تنها یکی از چند  ویژگی ماده است. با این وجود انرژی، تکانه خطی و تکانه زاویه ای همچنان به طور محکم در مرکز قرار دارند. اهمیت مستمر این اصول که از مکانیک کلاسیک به ارث رفته است ممکن است به توضیح اینکه چرا این موضوع اینقدر اهمیت زیادی در علم امروز دارد، کمک کند.

مکانیک تحلیلی چیست؟

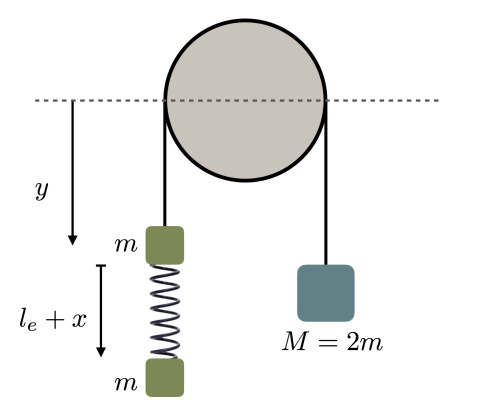
در مکانیک نیوتنی با معادلات مختلفی برای انواع حرکت جسم رو به رو می‌شویم. همان طور که بالاتر نیز بیان شد ساده‌ترین حالت این است که یک جسم نقطه‌ای را در نظر بگیریم که تحت تاثیر چندین نیرو حرکت می‌کند و با معادله برداری زیر بیان می‌شود:

$$\large \frac{d \overrightarrow{p}}{d t}=\overrightarrow{F}\ (1)$$

که در آن $$\overrightarrow p=m\overrightarrow v$$ است. این معادله حرکت را نمی‌توان از چند معادله دیگر استخراج کرد. معادله بالا به عنوان یک اصل یا یک حقیقت اساسی مکانیک نیوتنی در نظر گرفته شده است. همچنین می‌توان این دیدگاه را داشت که یکی از سه کمیت جرم سکون، نیرو و شتاب براساس دو کمیت دیگر تعریف شده است. معادله بالا یک معادله اساسی در مکانیک نیوتنی است. با این حال اگر حرکت یک جسم صلب را در نظر بگیریم معادله بالا به صورت زیر تغییر می‌کند و داریم:

$$\large \frac{d \overrightarrow{L}}{d t}=\overrightarrow{\tau} \ (2)$$

معادله بالا را می‌توان با تصور این که جسم از تعداد زیادی ذرات کوچک و تقریباً نقطه‌ای کنار هم قرار گرفته است که موقعیت نسبی آنها ثابت است (شرایط جسم صلب) به دست آورد. بیشترین چیزی که برای معادله بالا مورد نیاز است محدودیت سینماتیکی صلب و تعاریف مناسب برای حرکت زاویه‌ای یعنی L و گشتاور $$\tau$$ است.

همچنین در مکانیک نیوتنی اشکال مختلفی از معادله (1) را که در پایه‌های غیر خطی و به عنوان مثال مختصات قطبی نوشته می‌شود، دیده‌ایم. اگر چه ممکن است این معادله در مثلاً مختصات قطبی بلافاصله به عنوان معادله (1) قابل تشخیص نباشد اما با بررسی این اشکال از معادلات متوجه می‌شویم که این معادلات حاوی اطلاعات بیشتری نسبت به آنچه در معادله (1) نشان داده شده نیستند بلکه فقط نشان دهنده انتخاب مختصات مناسب برای برخی مسائل است. علاوه بر این ما با اصول انرژی، تکانه خطی و تکانه زاویه‌ای برخورد کرده‌ایم که می‌گوید در شرایط خاص برخی از این مقادیر بر حسب جرم و سرعت یعنی از نظر جنبشی با گذشت زمان تغییر نمی‌کنند یا در موارد دیگر میزان تغییر آن‌ها را پیش بینی می‌کنند. این‌ها مواردی است که می‌توان از معادله (1) یا مشتق آن یعنی معادله (2) استنباط کرد.

بدین ترتیب می‌توان دید که اگر چه تنوع زیادی از معادلات مختلف به دست آمده و مورد استفاده قرار می‌گیرد اما همه آنها دارای یک ریشه مشترک هستند و آن معادله حرکت یک ذره نقطه‌ای واحد است. مسأله موضوع مکانیک تحلیلی این است که همه اشکال مختلف معادلات حرکت را که در زمینه‌های مختلف اعمال می‌شوند را در یک موقعیت مساوی قرار دهیم. در حقیقت همه آن‌ها به صورت یکسان و مجموعه‌ای از معادلات یعنی معادله لاگرانژ و بعدها به صورت معادلات هامیلتونی بیان خواهند شد. همچنین این معادلات از یک اصل اساسی مشتق می‌شوند
که به آن اصل کنش می‌گوییم. این اصل به عنوان اصل اساسی مکانیک نیوتنی است و در حقیقت به عنوان اصل بسیاری از مدل‌ها از جمله مکانیک نسبیتی و نظریه‌های میدان نیز شناخته می‌شود.

همچنین یکی از مفیدترین و مهم‌ترین ویژگی‌های معادلات لاگرانژ و هامیلتونی را مشاهده خواهیم کرد و این ویژگی مهم این است که این دو کمیت مستقل از انتخاب مختصات، شکل یکسانی دارند. این امر این پارامترها را در برخورد با سیستم‌هایی که درجه آزادی مناسبی بر حسب متغیرهایی که معادلات حرکت نیوتن در آن‌ها به سختی قابل نوشتن است، برای مثال معرفی نیروهایی در مکانیک نیوتنی که تنها وظیفه آن‌ها برآورده ساختن شرایط سینماتیکی است، مثلاً نیرویی در طناب با طول ثابت و سیستم‌های محدود، بسیار قدرتمند می‌کند. در ادامه چندین نمونه از این نوع شرایط را بررسی می‌کنیم.

مختصات تعمیم یافته در مکانیک تحلیلی چیست؟

اساسی‌ترین ویژگی یک سیستم فیزیکی، درجه آزادی آن است. این حداقل تعداد متغیرهایی است که برای تعیین کامل موقعیت همه ذرات و اجسام بخشی از سیستم، یعنی پیکربندی آن در یک زمان معین مورد نیاز است. اگر تعداد درجات آزادی یک مجموعه N باشد هر مجموعه‌ای از متغیرهای $$q^1,\ . \ . \ . \ ,\ q^N$$ پیکربندی سیستم را مشخص می‌کند و مختصات تعمیم یافته سیستم نامیده می‌شود. توجه داشته باشید که نحوه حرکت سیستم در مختصات تعمیم یافته گنجانده نشده اما در مشتقات زمانی آن‌ها یعنی $$\dot{q}^1,\ . \ . \ . \ ,\ \dot{q}^N$$ وجود دارد.

برای مثال یک ذره در حال حرکت را در نظر بگیرید که یک درجه آزادی دارد. مختصات تعمیم یافته این ذره را می‌توان به صورت x نوشت. ذره‌ای که در سه راستا حرکت می‌کند دارای سه درجه آزادی است و مثالی از مختصات تعمیم یافته آن به صورت $$\overrightarrow{r}=(x,y,z)$$ است، این مختصات در سیستم کروی به صورت $$\overrightarrow{r}=(r,\theta,\phi)$$ است که $$x=r \sin \theta \cos \phi, \ y=r \sin \theta \sin \phi, \ z=r \cos \theta$$ نمایش داده می‌شود.

تعداد درجات آزادی برابر با تعداد معادلات حرکتی است که برای یافتن حرکت سیستم لازم است. گاهی اوقات بهتر است از تعداد بیشتری از مختصات نسبت به تعداد درجات آزادی یک سیستم استفاده کنیم. سپس مختصات باید از طریق نوعی معادله که قید نامیده می شود به یکدیگر مرتبط شوند. تعداد درجات آزادی در چنین حالتی برابر با تعداد مختصات تعمیم یافته منهای تعداد محدودیت‌ها است.

برای مثال یک پاندول را در نظر بگیرید که توسط دو مختصه مستقیم $$(x,y)$$ و یک جرم که به یک سر طناب بسته شده است، در نظر گرفته می‌شود. مختصات تعمیم یافته در این حالت زاویه است و درجه آزادی این سیستم یک است و $$(x,y)$$ توسط قید $$x^2+y^2=l^2$$ که $$l$$ طول طناب است به یکدیگر مرتبط می‌شوند.

به طور کلی مختصات تعمیم یافته با توجه به مسئله مورد نظر انتخاب می‌شود. اگر جسمی حول یک محور ثابت بچرخد، طبیعی‌ترین انتخاب برای مختصات تعمیم یافته زاویه چرخش است. اگر چیزی مستقیماً حرکت کند، مختصات خطی به عنوان مختصات تعمیم یافته استفاده می‌شود. برای سیستم‌های مرکب، انتخاب‌های طبیعی مختصات تعمیم یافته اغلب مخلوطی از انواع مختلف متغیرها است که متغیرهای خطی و زاویه‌ای رایج‌ترین آن‌ها هستند. قدرت سیستم لاگرانژی مکانیک نیوتن، همانطور که به زودی خواهیم دید این است که ماهیت مختصات تعمیم یافته در معادلات متناظر منعکس نمی‌شود و راه رسیدن به معادلات حرکت برای همه مختصات تعمیم یافته یکسان است.

سرعت تعمیم یافته نیز همانند سرعت عادی که از مختصات عادی به دست می‌آید، از مختصات تعمیم یافته استخراج می‌شود و داریم:

$$\large v^{i}=\dot{q}^{i}, \quad i=1, \ldots, N$$

دقت کنید که بُعد سرعت تعمیم یافته بستگی به بُعد مختصات تعمیم یافته دارد. در حالت کلی $$(v^1,\ .\ .\ .\ , v^N)$$ در یک سیستم متعامد، بردار سرعت نیستند. برای مثال در مختصات قطبی $$(r,\phi)$$ به عنوان مختصات تعمیم یافته، سرعت تعمیم یافته برابر با $$(\dot{r},\dot{\phi})$$ و بردار سرعت برابر با $$\dot{r} \hat{r}+r \dot{\phi} \hat{\phi}$$ است.

نیروهای تعمیم یافته چه هستند؟

فرض کنید که یک سیستم شامل تعدادی ذرات به صورت نقطه‌ای است که مختصات عادی آن‌ها برابر با $$x^1, .\ .\ .\ ,x^N$$ است. همچنین پیکربندی سیستم توسط مختصات تعمیم یافته $$q^1, .\ .\ .\ ,q^N$$ داده می‌شود. در این حالت نمی‌خواهیم تعداد ابعاد حرکت ذرات و در حقیقت تعداد درجات آزادی سیستم را مشخص کنیم.

این درجات آزادی می‌تواند برای n ذره که در صفحه حرکت می‌کنند برابر با $$N=2n$$ و برای m ذره که در سه بُعد حرکت می‌کنند $$N=3m$$ باشد. همچنین با توجه به اینکه هر دو مختصات بیان شده در بالا پیکربندی سیستم را مشخص می‌کنند، باید بین آن‌ها یک رابطه باشد که به صورت زیر بیان می‌شود:

$$\large \begin{aligned} &x^{1}=x^{1}\left(q^{1}, q^{2}, \ldots, q^{N}\right)=x^{1}(q) \\ &x^{2}=x^{2}\left(q^{1}, q^{2}, \ldots, q^{N}\right)=x^{2}(q) \\ &\vdots \\ &x^{N}=x^{N}\left(q^{1}, q^{2}, \ldots, q^{N}\right)=x^{N}(q) \end{aligned}$$

که در حالت فشرده این رابطه میان مختصات را می‌توان به صورت $$x^{i}=x^{i}(q)$$ نوشت. برای ایجاد ارتباط بین دو مجموعه متغیر که پیکربندی را کاملاً مشخص می‌کنند، توابع $$x^i$$ می‌توانند وابستگی زمانی مشخصی را شامل شوند که در این قسمت ترجیح می‌دهیم این توابع به زمان وابسته نباشند. اگر در متغیرهای $$q^i$$ یک جابجایی بی نهایت کوچک برابر با $$dq^i$$ ایجاد کنیم، قاعده مشتق زنجیره‌ای نشان می‌دهد که این جابجایی مربوطه در $$x^i$$ برابر است با:

$$\large d x^{i}=\sum_{j=1}^{N} \frac{\partial x^{i}}{\partial q^{j}} d q^{j}$$

کار انجام شده در این جابه‌جایی برابر با حاصلضرب نیرو و جابه‌جایی است که به صورت زیر بیان می‌شود و داریم:

$$\large d W=\sum_{i=1}^{N} F_{i} d x^{i}=\sum_{i=1}^{N} \mathscr{F}_{i} d q^{i}$$

که $$\mathscr{F}$$ برابر است با

$$\large \mathscr{F}_{i}=\sum_{j=1}^{N} F_{j} \frac{\partial x^{j}}{\partial q^{i}}$$

$$\mathscr{F}_i$$ برابر با نیروی تعمیم یافته است که به مختصات تعمیم یافته یعنی $$q^i$$ ارتباط دارد. همان طور که در مورد سرعت تعمیم یافته گفته شد، نیازی نیست که بُعد $$\mathscr{F}_i$$ همانند نیروی معمولی باشد. به عنوان مثال یک پاندول به طول $$l$$ را در نظر بگیرید که مختصات تعمیم یافته برای این پاندول $$\phi$$ است و به عنوان زاویه از محور عمودی شناخته می‌شود. فرض کنید که جرم $$m$$ تحت زاویه $$d\phi$$ و تحت اثر نیروی $$\overrightarrow{F}$$ حرکت می‌کند. جابه‌جایی این جرم برابر با $$d\overrightarrow{r}=l\ d\phi \ \hat{\phi}$$ و کار در این جابه‌جایی کوچک برابر با $$dW=\overrightarrow{F}.d\overrightarrow{r}=F_{\phi}ld\phi$$ است. نیروی تعمیم یافته که مرتبط با مختصات زاویه‌ای $$\phi$$ است برابر با $$\mathscr{F}_{\phi}=F_{\phi}l$$ بوده که دقیقاً برابر با گشتاور نیرو است. پس نتیجه‌ای که از این مثال حاصل می‌شود بسیار عمومی است و این است که نیروی تعمیم یافته برای مختصات زاویه‌ای برابر با گشتاور حرکت است. اگر نیرو پایستار باشد، از رابطه بین پتانسیل و نیرو داریم:

$$\large F_{i}=-\frac{\partial V}{\partial x^{i}}$$

اگر این رابطه را در رابطه مربوط به نیروی تعمیم یافته وارد کنیم خواهیم داشت:

$$\large \mathscr{F}_{i}=-\sum_{j=1}^{N} \frac{\partial V}{\partial x^{j}} \frac{\partial x^{j}}{\partial q^{i}}=-\frac{\partial V}{\partial q^{i}}$$

رابطه میان پتانسیل و نیروی تعمیم یافته به ازای هر مختصات تعمیم یافته شکل بالا را دارد.

انرژی جنبشی و تکانه تعمیم یافته چیست؟

در این قسمت بررسی می‌کنیم که انرژی جنبشی چه رابطه‌ای با مختصات تعمیم یافته و مشتقات آن یعنی سرعت تعمیم یافته دارد. یک تک ذره با جرم $$m$$ که در سه بُعد حرکت می‌کند در نظر بگیرید که در نتیجه درجات آزادی آن برابر با $$N=3$$ است. در این حالت انرژی جنبشی برابر است با:

$$\large T=\frac{1}{2} m \sum_{i=1}^{3}\left(\dot{x}^{i}\right)^{2}$$

در رابطه

$$\large \dot{x}^{i}=\sum_{j=1}^{3} \frac{\partial x^{i}}{\partial q^{j}} \dot{q}^{j}$$

نشان دادیم که $$\dot{x}^{i}$$ تابعی از $$q^j$$ است و $$\dot{q}^{j}$$ زمانی وارد می‌شود که مختصات به زمان وابسته باشد. بدین ترتیب می‌توان رابطه انرژی جنبشی را بر حسب مختصات و سرعت تعمیم یافته به شکل زیر نوشت و داریم:

$$\large T=\frac{1}{2} m \sum_{i, j=1}^{3} A_{i j}(q) \dot{q}^{i} \dot{q}^{j}$$

اگر بخواهیم این رابطه را بر حسب ساختار ماتریسی بنویسیم، داریم:

$$\large T=\frac{1}{2} m \dot{q}^{t} A \dot{q}$$

که در آن ماتریس A برابر است با:

$$\large A_{i j}=\sum_{k=1}^{3} \frac{\partial x^{k}}{\partial q^{i}} \frac{\partial x^{k}}{\partial q^{j}}$$

ذکر این نکته مهم است که بدانید اگر چه ممکن است که رابطه بین مختصات معمولی و مختصات تعمیم یافته غیرخطی باشد، اما رابطه انرژی جنبشی و سرعت تعمیم با ضریب $$A_{ij}$$ همواره خطی است و تنها به مختصات تعمیم یافته بستگی دارد. برای مثال حرکت در صفحه را برای مختصات قطبی در نظر بگیرید که داریم:

$$\large \begin{aligned} &x=r \cos \phi, \\ &y=r \sin \phi, \end{aligned}$$

بدین ترتیب ماتریس A برابر است با

$$\large A=\left[\begin{array}{ll} A_{r \tau} & A_{r \phi} \\ A_{r \phi} & A_{\phi \phi} \end{array}\right]=\left[\begin{array}{cc} 1 & 0 \\ 0 & r^{2} \end{array}\right]$$

و انرژی جنبشی به شکل شناخته شده زیر به دست می‌آید و داریم:

$$\large T=\frac{1}{2} m\left(\dot{r}^{2}+r^{2} \dot{\phi}^{2}\right)$$

اگر از انرژی جنبشی نسبت به یکی از سرعت‌ها در مختصات عادی (یعنی $$v^i=\dot{x}^i$$) دیفرانسیل بگیریم، داریم:

$$\large \frac{\partial T}{\partial \dot{x}^{i}}=m \dot{x}^{i}$$

که در حقیقت تکانه خطی به دست می‌آید. تکانه تعمیم یافته را به روشی مشابه می‌توان به صورت زیر نوشت و داریم:

$$\large p_{i}=\frac{\partial T}{\partial \dot{q}^{i}}$$

این حقیقت که تکانه تعمیم یافته به متغیرهای زاویه‌ای وابسته است نشان می‌دهد که تکانه زاویه‌ای یک کمیت عمومی است. در ادامه می‌خواهیم به معادلات حرکت برگردیم و آن‌ها را بر اساس مختصات تعمیم یافته فرمول بندی کنیم.

تابع لاگرانژ چیست؟

تابع لاگرانژی که لاگرانژین نیز نامیده می‌شود کمیتی است که وضعیت یک سیستم فیزیکی را مشخص می‌کند. در ابتدا تابع لاگرانژ را برای یک ذره منفرد بررسی می‌کنیم. همان طور که نشان دادیم معادله حرکت برای یک تک ذره توسط رابطه (1) داده می‌شود. در قسمت قبل نشان دادیم که چگونه تکانه از انرژی جنبشی یه دست می‌آید. بدین ترتیب معادله (1) را به شکل زیر و براساس مختصات تعمیم یافته بازنویسی می‌کنیم و داریم:

$$\large \frac{d}{d t} \frac{\partial T}{\partial \dot{x}^{i}}=F_{i}\ (3)$$

اولین حدس این است که اگر مختصات با مختصات تعمیم یافته و نیرو با نیروی تعمیم یافته جایگزین شود، چیزی مشابه معادله بالا به دست می‌آید. بنابراین ما سمت چپ معادله بالا را با q به جای x جایگزین می‌کنیم و داریم:

$$\large \begin{aligned} \frac{d}{d t} \frac{\partial T}{\partial \dot{q}^{i}} &=\sum_{j=1}^{3} \frac{d}{d t}\left(\frac{\partial T}{\partial \dot{x}^{j}} \frac{\partial \dot{x}^{j}}{\partial \dot{q}^{i}}\right)=\sum_{j=1}^{3} \frac{d}{d t}\left(\frac{\partial T}{\partial \dot{x}^{j}} \frac{\partial x^{j}}{\partial q^{i}}\right)=\\ &=\sum_{j=1}^{3}\left(\frac{\partial x^{j}}{\partial q^{i}} \frac{d}{d t} \frac{\partial T}{\partial \dot{x}^{j}}+\frac{d}{d t} \frac{\partial x^{j}}{\partial q^{i}} \frac{\partial T}{\partial \dot{x}^{j}}\right)=\sum_{j=1}^{3}\left(\frac{\partial x^{j}}{\partial q^{i}} \frac{d}{d t} \frac{\partial T}{\partial \dot{x}^{j}}+\frac{\partial \dot{x}^{j}}{\partial q^{i}} \frac{\partial T}{\partial \dot{x}^{j}}\right)=\\ &=\sum_{j=1}^{3} \frac{\partial x^{j}}{\partial q^{i}} \frac{d}{d t} \frac{\partial T}{\partial \dot{x}^{j}}+\frac{\partial T}{\partial q^{i}} \end{aligned}$$

در اینجا، ما از قواعد مشتق زنجیره‌ای و این واقعیت استفاده می کنیم که T در گام اول به $$\dot{x}^{i}$$ بستگی دارد و به $$x^i$$ وابسته نیست. سپس در مرحله دوم از این واقعیت که $$x^i$$ توابع $$q$$ هستند و نه $$\dot{q}^{i}$$ها برای بدست آوردن $$\frac{\partial{\dot{x}}^ j}{\partial \dot{q}^{i}}=\frac{\partial{x}^{j}}{\partial q^{i}}$$ استفاده می‌کنیم. در مرحله سوم دوباره از این موضوع برای استخراج رابطه $$\frac{d}{dt}\frac{\partial{x}^{j}}{\partial q^{i}}=\frac{\partial{\dot{x}}^ j}{\partial q^{i}}$$ استفاده می‌شود و در  آخرین مرحله دوباره مشتق زنجیره‌ای در T مورد استفاده قرار می‌گیرد. حال می‌توانیم معادله (3) را در معادلات حرکت ذره قرار دهیم و بدین ترتیب داریم:

$$\large \frac{d}{d t} \frac{\partial T}{\partial \dot{q}^{i}}=\sum_{j=1}^{3} \frac{\partial x^{j}}{\partial q^{i}} F_{j}+\frac{\partial T}{\partial q^{i}}$$

و در نهایت معادله لاگرانژ حرکت ذره به صورت زیر به دست می‎‌آید:

$$\large \frac{d}{d t} \frac{\partial T}{\partial \dot{q}^{i}}-\frac{\partial T}{\partial q^{i}}=\mathscr{F}_{i}$$

فرمالیزم لاگرانژی در زمانی که انرژی پتانسیل وجود دارد یعنی نیروها پایستار هستند و انرژی مکانیکی نیز پایستار است، بسیار مفید است. در نتیجه نیروی تعمیم یافته به صورت $$\mathscr{F}_{i}=-\frac{\partial V}{\partial q^{i}}$$ نوشته می‌شود و معادله لاگرانژ برابر است با:

$$\large \frac{d}{d t} \frac{\partial T}{\partial \dot{q}^{i}}-\frac{\partial T}{\partial q^{i}}+\frac{\partial V}{\partial q^{i}}=0$$

انرژی پتانسیل به سرعت تعمیم یافته وابسته نیست. در نتیجه اگر لاگرانژی را به شکل زیر بنویسیم:

$$\large L=T-V$$

معادلات را می‌توان به طور کامل و به صورت زیر بیان کرد:

$$\large \frac{d}{d t} \frac{\partial L}{\partial \dot{q}^{i}}-\frac{\partial L}{\partial q^{i}}=0$$

تابع L را تابع لاگرانژ یا لاگرانژین می‌نامیم. این شکل از معادلات حرکت یکی از رایج‌ترین شکل‌هایی است که برای حل مسائل مکانیک تحلیلی استفاده می‌شود. مشتق معادلات لاگرانژ در بالا بر اساس موقعیتی بود که مختصات تعمیم یافته $$q^i$$ استاتیک بودند، یعنی زمانی که تبدیل مختصات بین $$q^i$$ و مختصات لختی یعنی $$x^i$$ زمان را شامل نمی‌شد. این فرض بسیاری از موقعیت‌های مهم و مفید مانند سیستم‌های مختصات شتابدهنده یا چرخشی را حذف می‌کند. با این حال می‌توان ثابت کرد که معادلات لاگرانژ در مواردی که تغییر بین مختصات لختی و تعمیم یافته دارای وابستگی زمانی مشخص یعنی $$x^i=x^i(q;t)$$ است همچنان برقرار می‌ماند. در ادامه یک مثال بررسی می‌کنیم تا نشان دهیم معادلات لاگرانژ، هنگامی که در موقعیت‌های وابسته به زمان اعمال می‌شوند نیروهای لختی شناخته شده‌ای را بازتولید می‌کنند و از این امر به عنوان یک نتیجه گیری رسمی استفاده می‌کنیم. فقط این نکته را به ذهن داشته باشید که زمانی که لاگرانژی را شکل می‌دهید، انرژی جنبشی، انرژی جنبشی نسبت به سیستم لختی است.

یک ذره با جرم m در یک خط حرکت می‌کند. به جای استفاده از مختصات لختی x، می‌خواهیم از مختصات تعمیم یافته $$q=x-x_0(t)$$ استفاده کنیم که $$x_0(t)$$ توسط یک یا چند تابع مشخص می‌شود. برای مثال توضیح حرکت داخل یک ماشین که در حال حرکت بر روی یک مسیر مستقیم است و $$x_0(t)$$ موقعیت لختی ماشین است. همچنین تعریف می‌کنیم که $$v_0(t)=\dot{x}_0(t)$$ و $$a_0(t)=\ddot{x}_0(t)$$ است. بدین ترتیب انرژی جنبشی برابر است با:

$$\large T=\frac{1}{2} m\left(\dot{q}+v_{0}(t)\right)^{2}$$

در غیاب نیروها، لاگرانژی به شکل زیر در می‌آید و داریم:

$$\large 0=\frac{d}{d t} \frac{\partial T}{\partial \dot{q}}=m\left(\ddot{q}+a_{0}(t)\right)$$

در معادله بالا می‌توان دید که معادله مشهور نیروی لختی یعنی $$-ma_0(t)$$ به صورت اتوماتیک وار به دست آمده است. اگر چندین نیرو بر جسم اثر کنند، می‌توان نیروی تعمیم یافته را بر اساس نیروی لختی نوشت و داریم $$\mathscr{F}_{q}=F_{x}$$. نیروی تعمیم یافته $$\mathscr{F}_{q}$$ شامل نیروی لختی نیست.همان طور که گفتیم لاگرانژی را می‌توان برای سیستم‌های چند ذره‌ای یا بس ذره‌ای نیز بررسی کرد که در این مطلب از بحث در مورد آن صرف نظر می‌کنیم.

اصل کنش در مکانیک تحلیلی چیست؟

در این بخش اصلی را بررسی می‌کنیم که منجر به معادلات حرکت برای هر سیستم مکانیکی می‌شود. این اصل، اصل کنش است. برای فهم این اصل به کمی دانش ریاضیات نیاز داریم. فرض کنید که یک سیستم مکانیکی داریم و برای مثال فرض کنید یک ذره در پتانسیل در حال حرکت است و نمی‌دانیم مسیر حرکت ذره چگونه است. با این حال شرایط اولیه به این صورت است که ذره در زمان $$t_0$$ از مکان $$r(t_0)=\overrightarrow{r}_0$$ و با سرعت $$v(t_0)=\overrightarrow{v}_0$$ شروع به حرکت می‌کند. برای هر مسیر $$\overrightarrow{r}(t)$$ که شرایط اولیه را برآورده کند، $$S$$ را به صورت زیر تعریف می‌کنیم:

$$\large S=\int_{t_{0}}^{\infty} d t L$$

که L لاگرانژی و برابر با $$T-V$$ است. معادله بالا معادله کنش است. این معادله برای یک ذره با وجود پتانسیل به صورت زیر نوشته می‌شود:

$$\large S=\int_{t_{0}}^{\infty} d t\left[\frac{1}{2} m \dot{x}(t)^{2}-V(x(t))\right]$$

کنش یک تابع است که آرگومان‌های آن یک تابع و مقادیر در آن عدد هستند. اصل کنش بیان می‌کند که مسیر حرکت ذره باید یک نقطه استاتیک باشد. کنش به عنوان انتگرال لاگرانژ در بازه زمانی $$t_1$$ و $$t_2$$ برای یک مختصات تعمیم یافته $$q=(q_1, q_2, q_3, .\ .\ .\ , q_N)$$ تعریف می‌شود، که مختصات تعمیم یافته تابعی از زمان و مشخص کننده پیکربندی سیستم است.

معادلات هامیلتونی در مکانیک تحلیلی چگونه هستند؟

زمانی که معادلات لاگرانژ را به دست آوردیم، متغیرها و مختصاتی که مورد استفاده قرار دادیم مختصات تعمیم یافته و سرعت تعمیم یافته بودند. لاگرانژ L به عنوان تابعی از این متغیرها به صورت $$L(q^i,\dot{q}^i)$$ نوشته می‌شود. این مجموعه از متغیرها یکتا نیستند و برای هر حالت یک انتخاب وجود دارد که به هامیلتونی سیستم بستگی پیدا می‌کند.

معادلات هامیلتونی معمولاً در مکانیک کوانتومی نیز مورد استفاده قرار می‌گیرند. همان طور که در قسمت‌های قبل نیز گفته شد، تکانه مرتبط با مختصات $$q^i$$ به صورت زیر معرفی می‌شود:

$$\large p_{i}=\frac{\partial L}{\partial \dot{q}^{i}}$$

در یک مختصات خط راست همان طور که دیدیم تکانه معمولی برابر با $$p_i=m\dot{q}^i$$ بود، ولی این موضوع برای مختصات‌های تعمیم یافته دیگر صدق نمی‌کند. در حال حاضر می‌خواهیم متغیرهای پایه را از مختصات $$q^i$$ و سرعت $$v^i$$ به مختصات و تکانه $$p_i$$ تغییر دهیم. به زودی خواهید دید که در زمان تغییر متغیرها اینکه عملگر دیگری غیر از لاگرانژین را در نظر بگیرید، طبیعی است. برای این حالت، شرایطی را در نظر بگیرید که تنها دارای یک مختصات $$q$$ است. دیفرانسیل لاگرانژی $$L(q,v)$$ در این حالت برابر است با:

$$\large d L=\frac{\partial L}{\partial q} d q+\frac{\partial L}{\partial v} d v=\frac{\partial L}{\partial q} d q+p d v$$

در مرجعی که مختصات اصلی و پایه $$q$$ و $$p$$ هستند، دیفرانسیل تابع به صورت طبیعی برابر با $$adq+bdp$$ است که a و b می‌توانند هر مقداری داشته باشند. تابع جدید H را به صورت زیر در نظر بگیرید:

$$\large H=v p-L=\dot{q} p-L$$

H هامیلتونی است و دیفرانسیل آن برابر است با:

$$\large d H=d v p+v d p-d L=d v p+v d p-\frac{\partial L}{\partial q} d q-p d v=-\frac{\partial L}{\partial q} d q+v d p$$

بنابراین داریم:

$$\large \frac{\partial H}{\partial q}=-\frac{\partial L}{\partial q}, \quad \frac{\partial H}{\partial p}=v=\dot{q}$$

تغییر عملگر به شکل بالا که با تغییر متغیر به این صورت همراه است را تبدیلات لژاندر می‌نامیم. دقت کنید که وقتی متغیرها را به q و p تغییر می‌دهید، باید تابع H را نیز بر اساس متغیرهای جدید بیان کنیم و بنابراین هر استفاده از v حذف می‌شود. بدین ترتیب با استفاده از معادله لاگرانژ که به صورت $$\frac{\partial L}{\partial q}=\dot{p}$$ است، معادلات هامیلتونی برابر است با:

$$\large \dot{q}=\frac{\partial H}{\partial p}, \quad \dot{p}=-\frac{\partial H}{\partial q}$$

برای سیستم‌های چند ذره‌ای نیز هامیلتونی به راحتی به دست می‌آید و تنها لازم است از یک اندیس i برای هر کمیت استفاده کنیم و در نتیجه داریم:

$$\large \begin{gathered} H=\sum_{i} \dot{q}^{i} p_{i}-L \\ \dot{q}^{i}=\frac{\partial H}{\partial p_{i}}, \quad \dot{p}_{i}=-\frac{\partial H}{\partial q^{i}} \end{gathered}$$

این مطلب را با بررسی یک مثال به پایان می‌بریم. یک سیستم خطی در نظر بگیرید که در آن $$T=\frac{1}{2}m\dot{x}^2$$ و $$L=\frac{1}{2}m\dot{x}^2-V(x)$$ باشد. در نتیجه $$\frac{\partial L}{\partial \dot{x}}=m\dot{x}$$ است و داریم:

$$\large H=\dot{x} p-L=\frac{p^{2}}{m}-\frac{1}{2} m\left(\frac{p}{m}\right)^{2}+V(x)=\frac{p^{2}}{2 m}+V(x)$$

که مجموع انرژی پتانسیل و جنبشی است. این بیان حقیقتاً تا زمانی که وابستگی صریح زمانی بین L و زمان وجود ندارد، کلی است. در نتیجه معادلات هامیلتونی به شکل زیر در می‌آیند و داریم:

$$\large \dot{x}=\frac{\partial H}{\partial p}=\frac{p}{m}, \quad \dot{p}=-\frac{d V}{d x}$$

دقت کنید که به جای معادلات دیفرانسیل درجه 2 در رابطه بالا معادلات دیفرانسیل درجه 1 داریم. معادله اول برحسب $$p$$ است و وقتی در معادله دوم قرار داده می‌شود به صورت زیر خواهد بود:

$$\large m \ddot{x}=-\frac{d V}{d x}$$

منابع برتر برای مطالعه مکانیک تحلیلی چه کتاب‌هایی هستند؟

در این قسمت ده منبع معتبر در مکانیک تحلیلی که توسط دانشجویان در موسسات و مراکز معتبر مورد استفاده قرار می‌گیرند را معرفی می‌کنیم.

مکانیک کلاسیک اثر گلداشتاین

این کتاب مروری کلی بر مکانیک کلاسیک و همچنین مقایسه‌ای بین فیزیک کلاسیک و مدرن ارائه می‌دهد. موضوعات این کتاب شامل مثال‌های متعدد در دنیای واقعی است و شامل بسیاری از مثال‌های حل شده و حل نشده با توضیحات دقیق است. اصول ابتدایی مکانیک تحلیلی، معادله لاگرانژ، مشکلات نیرو مرکزی، سینماتیک حرکت اجسام صلب، نوسانات، نظریه نسبیت خاص، معادله حرکت هامیلتون، تبدیلات کانونیکال و موارد دیگر از مواردی است که در این کتاب بحث و معرفی شده است. این کتاب برای آموزش دانشجویان، اساتید و متخصصان در زمینه‌های مختلف مهندسی و علوم تالیف شده است. سرفصل‌های این کتاب و جزئیات بیشتر را می‌توانید در اینجا ببینید.

دینامیک کلاسیک اثر گرین وود

این کتاب مروری اساسی بر دینامیک کلاسیک ارائه می‌دهد و اساس و بنیاد دینامیک تحلیلی، نظریه‌های همیلتون و ژاکوبی، نظریه نسبیت اینشتین و بسیاری دیگر از نظریه‌های مکانیک کلاسیک را توضیح می‌دهد. این کتاب شامل مثال‌های حل شده و حل نشده متعددی با توضیحات نظری و ریاضی است. مفاهیم در این کتاب با این فرض است که خواننده با مکانیک بردار و اصول چرخش جسم صلب در دو بعد آشنایی اساسی دارد. این کتاب با تمرکز بر آموزش دانشجویان، اساتید و متخصصان در زمینه مهندسی و علوم طراحی شده است. سرفصل‌های این کتاب و جزئیات بیشتر را می‌توانید در اینجا ببینید.

دینامیک لاگرانژی اثر ولز

این کتاب مفاهیم دینامیک لاگرانژی را با جزئیات پوشش می‌دهد. در حقیقت در این کتاب اصول اساسی دینامیک لاگرانژی توضیح داده می‌شود و آموزش‌هایی در این زمینه در مورد تکنیک‌های فیزیکی و ریاضی واقعی ارائه می‌دهد. این کتاب اساس مطالعه برای موضوعاتی است که فاصله بین فیزیک کلاسیک و کوانتوم، مهندسی، شیمی و ریاضیات کاربردی را پر می‌کند. در این کتاب مثال‌های حل شده و حل نشده متعددی با توضیحات نظری و ریاضی دقیق ارائه داده شده است. چالش‌های پیش روی دینامیک لاگرانژی و راه‌های حل آن نیز در این کتاب توضیح داده شده است. سرفصل‌های این کتاب و جزئیات بیشتر را می‌توانید در اینجا ببینید.

مکانیک تحلیلی: راه حل مسائل فیزیک کلاسیک توسط دنیل رادو

این کتاب در مورد اصول و روش‌های مکانیک تحلیلی به تفصیل صحبت می‌کند و مشکلات اساسی موجود در مکانیک تحلیلی را توضیح می‌دهد و راه حل‌هایی را برای آن‌ها ارائه می‌دهد. این کتاب شامل مثال‌های حل شده و حل نشده متعددی است. در این کتاب دانشجویان در استفاده از نظریه برای مسائل فیزیک کلاسیک با استفاده از حساب تغییرات، نظریه تعادل، فرمالیسم لاگرانژی و هامیلتونی برای سیستم‌های گسسته و پیوسته، روش همیلتون-ژاکوبی و موارد دیگر تجربه کسب می‌کنند. همچنین این کتاب اصول اولیه جبر بردار و تحلیل بردار را پوشش می‌دهد. مباحث این کتاب برای دانشجویان و اساتید در زمینه مهندسی و علوم بسیار مفید است. سرفصل‌های این کتاب و جزئیات بیشتر را می‌توانید در اینجا ببینید.

مکانیک تحلیلی برای نسبیت و مکانیک کوانتومی نوشته اولیور جانس

این کتاب پایه و اساس مکانیک تحلیلی و ارتباط مکانیک کلاسیک با نسبیت و نظریه کوانتوم را ارائه می‌دهد. مفاهیم این کتاب به گونه‌ای طراحی شده است تا برای دانشجویان و اساتید دوره‌های کارشناسی مهندسی و علوم مفید باشد. این کتاب به زبانی قابل فهم نوشته شده است و مثال‌های حل شده و حل نشده متعددی با توضیحات مفاهیم نظری و ریاضی ارائه می‌دهد. این کتاب موضوعات مکانیک تحلیلی، نسبیت و مکانیک کوانتومی را با استفاده از مثال‌های واقعی پوشش می‌دهد و همچنین شامل تصاویر، معادلات ریاضی و نمودارهایی است که برای درک بهتر خواننده استفاده شده است. سرفصل‌های این کتاب و جزئیات بیشتر را می‌توانید در اینجا ببینید.

مقدمه‌ای بر مکانیک تحلیلی توسط K A I L W Gamalath

این کتاب مروری اساسی بر مکانیک تحلیلی دارد و دارای مفاهیمی مانند دینامیک لاگرانژی، مکانیک نیوتنی، قوانین پایستگی و سایر موارد است. توضیحات نظری و ریاضی در این کتاب درک خواننده را از این مفاهیم افزایش می‌دهد. این کتاب شامل مثال‌های حل شده و حل نشده متعددی است که با نمودارها، معادلات و اشکال برای درک بهتر موضوع ارائه می‌شود. این کتاب به زبانی قابل فهم نوشته شده است و انتظار ندارد خواننده در این زمینه پیش زمینه‌ای داشته باشد و برای دانشجویان و اساتید در زمینه مهندسی مکانیک که به طور منظم با مکانیک تحلیلی سر و کار دارند، مفید است. سرفصل‌های این کتاب و جزئیات بیشتر را می‌توانید در اینجا ببینید.

مکانیک تحلیلی توسط V N Vagliente

این کتاب به بررسی اجمالی مکانیک تحلیلی می‌پردازد و به زبانی قابل فهم نوشته شده است. این کتاب در ابتدا مبانی مکانیک را پوشش می‌دهد و سپس به سراغ موضوعات پیچیده می‌رود. همچنین در مورد الگوریتم‌های ژاکوب برنولی، دانیل برنولی، لئونارد اویلر، الکسیس کلیروت و دیگران در این کتاب بحث شده است. همچنین در این کتاب جزئیاتی در مورد تعامل محدود یا مقید، جریان سیال، کشش، مقاومت مواد و عملکرد ماشین آلات ارائه شده است. این کتاب شامل مثال‌های حل شده و حل نشده متعددی است و برای دانشجویان، اساتید و متخصصان در زمینه مهندسی و علوم طراحی شده است.

مکانیک تحلیلی اثر استفانو مارمی و آنتونیو فاسان

این کتاب به بررسی اجمالی مکانیک تحلیلی می‌پردازد و انتظار می‌رود که خواننده اصول اولیه موضوع را درک کند. در این کتاب فاصله بین مفاهیم اولیه مکانیک تحلیلی و مفاهیم پیشرفته پوشش داده شده و برای مسائل راه حل‌های نظری و ریاضی ارائه می‌شود. این کتاب شامل مثال‌های حل شده و حل نشده متعددی با توضیحات مفصل برای درک بهتر آن است. این کتاب برای دانشجویان، اساتید و متخصصان در زمینه مهندسی و علوم طراحی شده است. سرفصل‌های این کتاب و جزئیات بیشتر را می‌توانید در اینجا ببینید.

مکانیک تحلیلی اثر A I Lurie

این کتاب به بررسی اجمالی مکانیک تحلیلی می‌پردازد و مفاهیم اولیه و پیشرفته را به زبانی آسان برای فهم بیشتر پوشش می‌دهد. در این کتاب اصول اولیه، معادله لاگرانژ، مشکل نیرو مرکزی، سینماتیک حرکت جسم صلب و موارد دیگر پوشش داده می‌شود. این کتاب شامل مثال‌های متعدد در دنیای واقعی و مشکلات حل شده و حل نشده برای درک بیشتر است. تصاویر، نمودارها، اشکال برای توضیحات ریاضی و نظری مسائل پیچیده در این کتاب ارائه شده است. این کتاب برای دانشجویان، اساتید و متخصصان در زمینه مهندسی و علوم مفید است. سرفصل‌های این کتاب و جزئیات بیشتر را می‌توانید در اینجا ببینید.

هندسه سیمپلکتیک و مکانیک تحلیلی اثر لیبرمن و مارل

این کتاب به بررسی اجمالی مکانیک تحلیلی می‌پردازد و شامل مفاهیم مرتبط با دینامیک لاگرانژی، فرمالیسم‌های هامیلتونی، مکانیک نیوتنی، قوانین پایستگی و موارد دیگر با جزئیات است. در این کتاب توضیحات نظری و ریاضی برای افزایش درک خواننده ارائه شده و شامل مثال‌های حل شده و حل نشده متعددی با نمودارها، معادلات و اشکال برای خوانایی بهتر است. انتظار می‌رود که خوانندگان دانش اولیه‌ای از هندسه سمپلتیک و مکانیک تحلیلی داشته باشند. این کتاب برای دانشجویان، اساتید و متخصصان در زمینه مهندسی و علوم طراحی شده است. سرفصل‌های این کتاب و جزئیات بیشتر را می‌توانید در اینجا ببینید.

معرفی فیلم‌های مکانیک تحلیلی فرادرس

در ادامه برخی آموزش‌های مکانیک تحلیلی را که برای رشته‌های فیزیک، مکانیک و مهندسی آماده شده است را معرفی می‌کنیم. این فیلم‌های و دوره‌های ویدیویی در کنار یک منبع اصلی می‌تواند کمک شایانی برای دانشجویان این رشته‌ها به همراه داشته باشد.

معرفی فیلم آموزش مکانیک تحلیلی ۱ (Analytical Mechanics)

مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم آموزش مکانیک تحلیلی ۱ (Analytical Mechanics) کرده است. این مجموعه آموزشی از هفت درس تشکیل شده و برای دانشجویان رشته فیزیک و مهندسی مکانیک مفید است. پیش‌نیاز این درس آموزش ریاضی فیزیک و معادلات دیفرانسیل است.

درس اول این مجموعه به آموزش ‌مفاهیم بنیادی، بردارها و درس دوم به بررسی مکانیک نیوتونی، حرکت راست خط ذره می‌پردازد. درس سوم به نوسانگر هماهنگ و درس چهارم به حرکت کلی ذره در سه بعد اختصاص دارد. در درس پنجم و ششم به ترتیب دستگاه‌های مرجع نالخت و نیروهای مرکزی و مکانیک سماوی را خواهید آموخت و در درس هفتم و آخر این مجموعه مفاهیم مربوط به دینامیک سیستم‌های ذرات بررسی می‌شود.

• برای دیدن آموزش مکانیک تحلیلی ۱ (Analytical Mechanics) +‌ اینجا کلیک کنید.

معرفی فیلم آموزش مکانیک تحلیلی ۲

مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم آموزش مکانیک تحلیلی ۲ کرده است. این مجموعه آموزشی از هفت درس تشکیل شده و برای دانشجویان رشته فیزیک و مهندسی مکانیک مفید است. پیش‌نیاز این درس آموزش فیزیک پایه ۱، آموزش ریاضی عمومی ۲، معادلات دیفرانسیل و آموزش مکانیک تحلیلی 1 است.

درس اول این مجموعه به حرکت در چارچوب نالخت می‌پردازد و درس دوم روش های حساب وردشی (حساب تغییرها) را بررسی می‌کند. درس سوم به مسائل مربوط به اصل هامیلتون، دینامیک لاگرانژی و همیلتونی و درس چهارم به بررسی حرکت نیروی مرکزی اختصاص دارد. در درس پنجم و ششم این مجموعه به ترتیب بررسی و تحلیل مسائل در زمینه دینامیک اجسام صلب و نوسان‌های جفت شده را خواهید آموخت. در نهایت درس هفتم و آخر این مجموعه به بررسی نمونه سوالات کنکور کارشناسی ارشد درس مکانیک تحلیلی 2 اختصاص دارد.

• برای دیدن آموزش مکانیک تحلیلی ۲ +‌ اینجا کلیک کنید.

معرفی فیلم آموزش مکانیک تحلیلی ۱ (مرور و حل مثال)

مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم آموزش مکانیک تحلیلی ۱ (مرور و حل مثال) کرده است. این مجموعه آموزشی از نه درس تشکیل شده و برای دانشجویان رشته فیزیک مفید است. پیش‌نیاز این درس آموزش فیزیک پایه ۱ است.

درس اول این مجموعه به معرفی مفاهیم بنیادی در مکانیک نیوتنی و درس دوم به بررسی حرکت روی خط مستقیم می‌پردازد. درس سوم به حرکت یک بعدی ذره (قضیه‌های اندازه حرکت و انرژی جنبشی) و درس چهارم به شناخت انواع نیرو اختصاص دارد. در درس پنجم و ششم به ترتیب نوسانگرها و حرکت دوبعدی را خواهید آموخت و در درس هفتم مفاهیم مربوط به حرکت سه بعدی (دستگاه مختصات استوانه‌ای) بررسی می‌شود. درس هشتم این مجموعه به آموزش مفاهیم حرکت سه بعدی (دستگاه مختصات کروی) می‌پردازد و در نهایت درس نهم به مطالب حرکت ذره تحت تأثیر نیروی مرکزی اختصاص دارد.

• برای دیدن آموزش مکانیک تحلیلی ۱ (مرور و حل مثال) +‌ اینجا کلیک کنید.

جمع‌بندی

در این مطلب در مورد مکانیک تحلیلی صحبت کردیم. بدین منظور ابتدا مفاهیم اولیه و ابتدایی مرتبط با مکانیک تحلیلی را به صورت مختصر معرفی کردیم و سپس به معرفی منابع برتر در زمینه مکانیک تحلیلی پرداختیم. در نهایت آموزش‌های ویدیویی را که به دانشجویان در یادگیری بهتر و آسان‌تر مکانیک تحلیلی کمک می‌کند و توسط فرادرس منتشر شده است را معرفی کردیم.