امواج الکترومغناطیسی – از صفر تا صد

پیش‌تر در بلاگ فرادرس، معادلات ماکسول و نحوه بدست آوردن آن‌ها را توضیح دادیم. در این قسمت قصد داریم تا از این معادلات، استفاده کرده و امواج الکترومغناطیسی را تعریف و توصیف کنیم. به دو میدان الکتریکی و مغناطیسی عمود به هم، که با زمان و مکان نوسان کرده و در جهتی خاص حرکت می‌کنند، موج الکترومغناطیسی گفته می‌شود. در ادامه در مورد ویژگی این دو میدان عمود به هم و ارتباط آن‌ها با یکدیگر بحث خواهد شد. همچنین پیشنهاد می‌کنیم جهت آشنایی با انواع مختلف امواج الکترومغناطیسی به مقاله «طیف الکترومغناطیسی — به زبان ساده» رجوع کنید.

امواج الکترومغناطیسی تخت

جهت بررسی ویژگی‌های امواج الکترومغناطیسی، مطابق با انیمیشن زیر موجی را در نظر بگیرید که در جهت مثبت محور x در حرکت است.

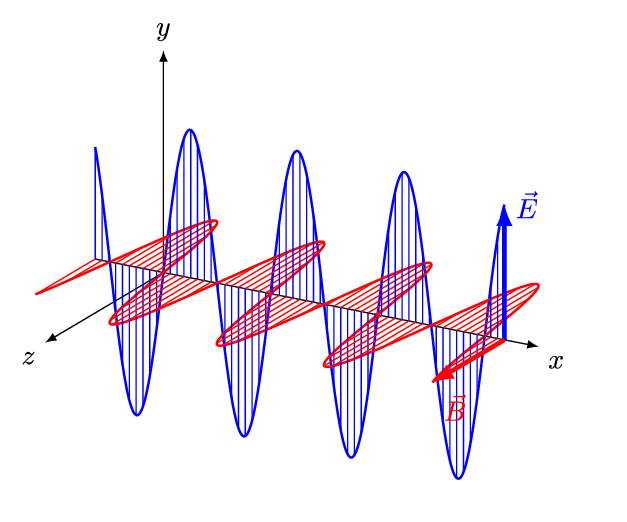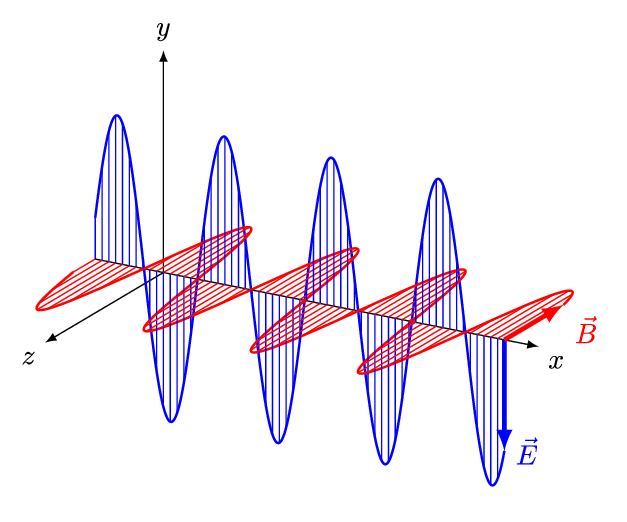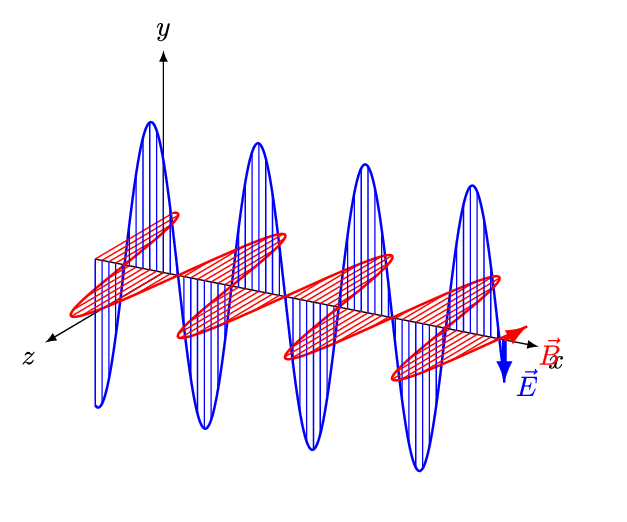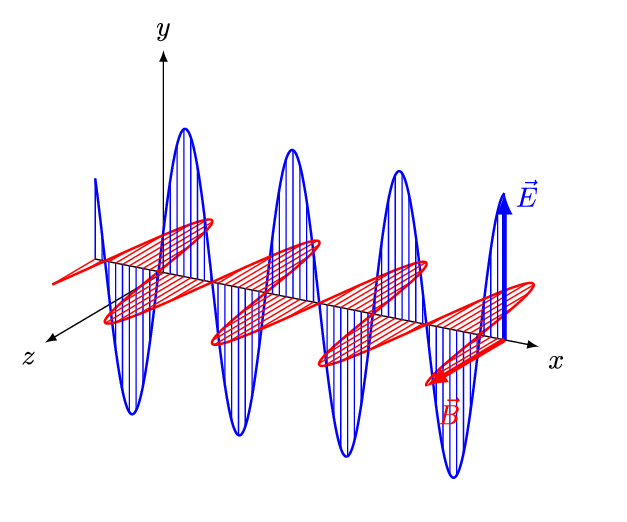
مطابق با انیمیشن بالا اندازه میدان الکتریکی (E) در راستای y و اندازه میدان مغناطیسی (B) در راستای z با زمان تغییر می‌کنند. موجی که در بالا شرح داده شد، نمونه‌ای از یک موج تخت محسوب می‌شود. هم‌چنین با توجه به این که هر دو میدان به جهت انتشار عمود هستند، به این نوع از موج، موج عرضی نیز گفته می‌شود. در امواج عرضی، جهت انتشارِ موج، در جهت بردار یکه $$\overrightarrow{E}×\overrightarrow{B}$$ است.

با استفاده از معادلات ماکسول، می‌توان اندازه ‌میدان‌های الکتریکی و مغناطیسی را یافت. بدین منظور مطابق با تصویر زیر منحنی مستطیلی شکلی را در صفحه x-y در نظر بگیرید.

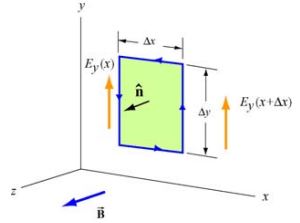
سمت چپ حلقه در موقعیت x و سمت راست در x+Δx قرار گرفته است. پایین حلقه نیز در y و بالای آن در y+Δy است. جهت ساده‌سازی، بردار عمود به حلقه را برابر با $$\widehat{n}=\widehat{k}$$ تصور کنید. با نوشتن قانون القای فارادی برای صفحه تشکیل شده از این حلقه داریم:

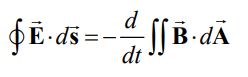
سمت چپ معادله بالا برابر است با:

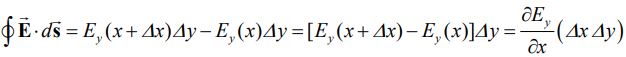
در رابطه بالا از بسط تیلور زیر استفاده شده:

از طرفی نرخ تغییرات میدان مغناطیسی در دیفرانسیل dA برابر است با:

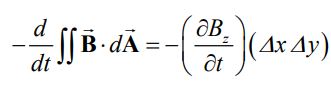
با برابر قرار دادن رابطه ۱ و ۲ و تقسیم کردن آن‌ها به Δy داریم:

رابطه بالا تغییرات میدان الکتریکی در مکان را بر حسب تغییرات میدان مغناطیسی در زمان نشان می‌دهد. اگر بخواهیم تغییرات میدان الکتریکی را در زمان بر حسب میدان مغناطیسی بیان کنیم، حلقه‌ای را مطابق با شکل زیر در نظر می‌گیریم.

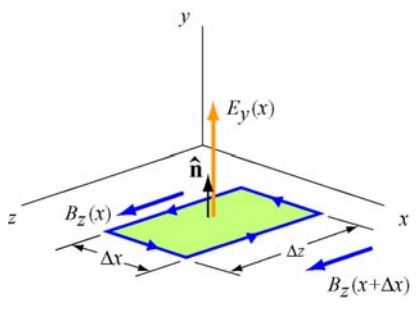
رابطه آمپر-ماکسول برای یک حلقه آمپری را در مطلب معادلات ماکسول مطابق با رابطه زیر ارائه کردیم.

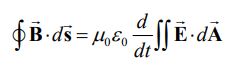
همان‌طور که در شکل ۱ نیز نشان داده شده، بردار عمود بر صفحه به‌صورت $$\widehat{n}=\widehat{j}$$ است. انتگرال خطی میدان مغناطیسی رو حلقه (سمت چپ رابطه بالا) برابر است با:

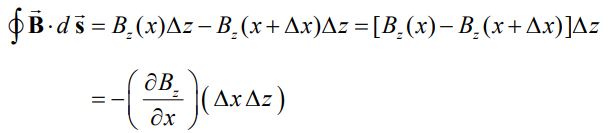
از طرفی مشتق زمانی شار الکتریکی برابر است با:

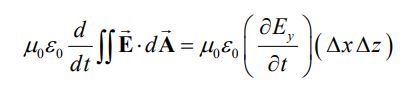
با برابر قرار دادن دو رابطه بالا و تقسیم کردن آن‌ها به x∆z∆ رابطه تغییرات زمانی میدان الکتریکی بر حسب تغییرات مکانی میدان مغناطیسی، به صورت زیر بدست می‌آید.

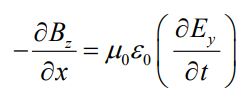
نتیجه بالا نشان می‌دهد که تغییرات مکانی میدان مغناطیسی منجر به ایجاد میدان الکتریکی می‌شود.

با استفاده از روابط ۲ و ۴ می‌توان نشان داد که هر دو میدان الکتریکی و مغناطیسی قادرند تا در معادله یک‌بعدی موج قرار گیرند. جهت نشان دادن این موضوع، در ابتدا از رابطه ۳ نسبت به x و از رابطه ۵ نسبت به t مشتق می‌گیریم. با این مشتق‌گیری داریم:

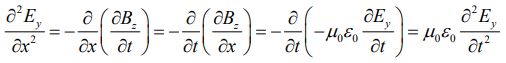
توجه داشته باشید که در رابطه بالا از قابلیت جابجایی متغیر‌ها به شکل زیر استفاده شده است.

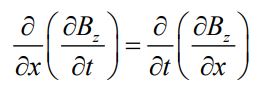
مشابه با روش بالا، در این مرحله از رابطه ۵ نسبت به x و از رابطه ۳ نسبت به t مشتق می‌گیریم. با انجام این کار داریم:

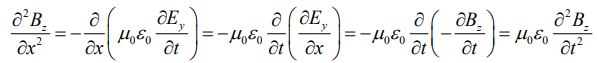
در نتیجه خلاصه روابط ۶ و ۷ را می‌توان به‌شکل زیر بیان کرد:

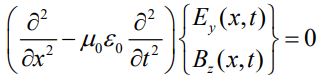
توجه داشته باشید که از مکانیک می‌دانیم که رابطه مربوط به انتشار موجی یک‌بعدی به صورت زیر است:

در رابطه بالا v سرعت موج و $$\psi (x,t)$$  نشان دهنده تابع موج است. با توجه به رابطه بالا و برابر قرار دادن آن با رابطه۸ می‌توان سرعت انتشار امواج الکترومغناطیسی را برابر با مقدار زیر بدست آورد.

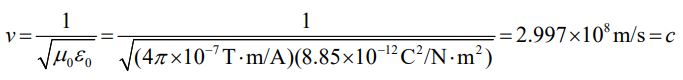
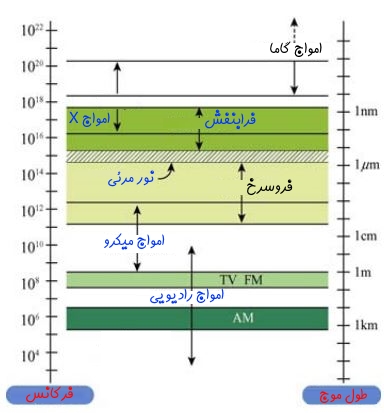
پاسخ بالا نشان می‌دهد که امواج الکترومغناطیسی با سرعت نور منتشر می‌شوند. هم‌چنین خود نور نیز نوعی موج الکترومغناطیسی است. طیف الکترومغناطیسی امواج مختلف در جدول زیر نشان داده شده است.

معادله موج تک‌ بعدی

می‌توان به طور مستقیم اثبات کرد که هر تابعی به صورت (ψ(x±vt در معادله موج صادق خواهد بود. این بیان در ادامه اثبات شده است. جهت اثبات، در ابتدا متغیر x'=x±vt را تعریف می‌کنیم. با استفاده از این تعریف، مشتقات زمانی و مکانی این متغیر به صورت $$\partial x'/\partial x=1$$ و $$\partial x'/\partial t=±v$$ خواهند بود. در نتیجه با استفاده از قانون مشتق‌گیری زنجیره‌ای داریم:

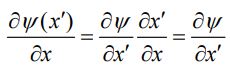
در نتیجه مشتق دوم ('ψ(x برابر است با:

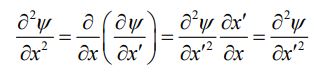
با روشی مشابه مشتق‌گیری زمانی تابع $$\psi (x')$$ را می‌توان نسبت به زمان و مطابق با عبارت زیر بدست آورد.

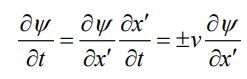
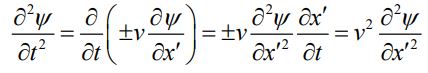
با مقایسه رابطه ۹ و ۱۰ داریم:

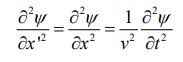
عبارت بالا نشان می‌دهد که $$\psi (x±vt)$$ در رابطه موج یک‌بعدی صدق می‌کند. معادله موج مثالی از معادله دیفرانسیلی خطی است؛ در نتیجه که اگر $$\psi_1 (x,t)$$ و $$\psi_2 (x,t)$$ پاسخ‌های معادله دیفرانسیل مذکور باشند، در این صورت $$\psi_1 (x,t) + \psi_2 (x,t)$$ نیز در معادله دیفرانسیل موج صادق خواهند بود.

بنابراین تا به این‌جا دو معادله را برای یک موج الکترومغناطیسی مطابق با رابطه زیر یافتیم و ثابت کردیم که هر کدام از آن‌ها موجی تک‌ بعدی هستند [یک معادله برای میدان الکتریکی و یک معادله برای میدان مغناطیسی].

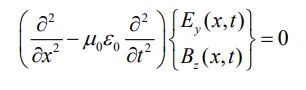
یکی از پاسخ‌های ممکن برای دو معادله بالا به صورت زیر است:

مطابق با رابطه بالا، تغییرات میدان‌ها به صورت سینوسی در نظر گرفته شده و دامنه آن‌ها نیز برابر با E₀ و B₀ فرض شده‌اند. مقدار k یا همان عدد موج را می‌توان بر حسب طول موجِ λ، بصورت زیر بیان کرد:

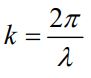
فرکانس زاویه‌ای ω نیز برابر است با:

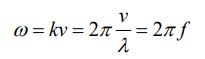
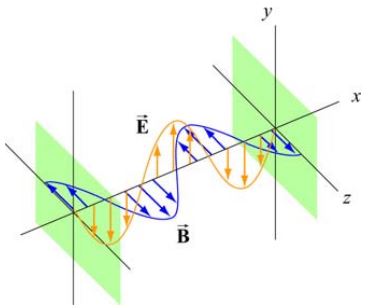
در رابطه بالا f برابر با فرکانس خطی موج است. در فضای خالی (خلاء) سرعت موج الکترومغناطیسی برابر با سرعت نور است (v=c). نمونه‌ای از یک موج الکترومغناطیسیِ سینوسی در شکل زیر نشان داده شده است.

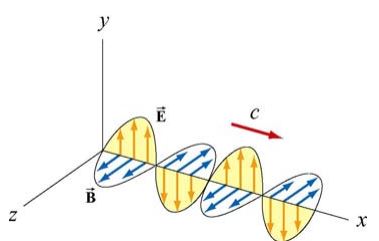
همان‌طور که در شکل بالا نیز می‌بینید، در یک موج تخت میدان‌های $$\overrightarrow{B}$$ و $$\overrightarrow{E}$$ همواره هم‌فاز هستند. در حقیقت در یک زمان و مکان، میدان‌های الکتریکی و مغناطیسی ماکزیمم شده و در یک زمان نیز می‌نیمم می‌شوند. جهت بدست آوردن مقادیر E₀ و B₀ بر حسب یکدیگر، می‌توان از معادلات معرفی شده برای میدان مغناطیسی و الکتریکی به‌شکل زیر مشتق جزئی گرفت:

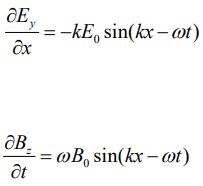
از طرفی در بالا رابطه زیر را نشان دادیم:

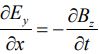
با برابر قرار دادن دو معادله معرفی شده در رابطه ۱۱، به عبارت E₀k=ωB₀ می‌رسیم؛ در نتیجه رابطه بین دامنه دو میدان به‌شکل زیر بدست می‌آید.

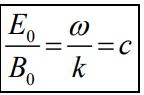
معادلات بالا ویژگی‌ موج‌های تخت عرضی را توصیف می‌کنند. ویژگی اصلی این نوع از موج‌ها به‌طور خلاصه به شرح زیر هستند:

1. این نوع موج به صورت عرضی است. دلیل عرضی بودن آن‌ها این است که میدان‌های مغناطیسی و الکتریکی در هر لحظه به یکدیگر عمود بوده و جهت انتشار آن‌ها نیز به جهت حرکت موج عمود است. در حقیقت جهت انتشار موج در جهت بردار یکه $$\widehat{E}×\widehat{B}$$ است.
2. حاصلضرب داخلی دو بردار $$\overrightarrow{E}$$ و $$\overrightarrow{B}$$ در هر لحظه برابر با صفر است.
3. نسبت اندازه دامنه میدان‌ها برابر است با:
   
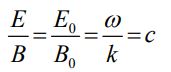
4. سرعت انتشار این موج در خلاء برابر با سرعت نور یا همان $$\Large {1} \over \Large {\sqrt{\mu_0 \epsilon_0}}$$ است.
5. امواج الکترومغناطیسی از قانون جمع آثار پیروی می‌کنند.

امواج الکترومغناطیسی ایستا

دو موج الکترومغناطیسی را تصور کنید که یکی از آن‌ها مطابق با رابطه زیر در جهت x+ حرکت می‌کند.

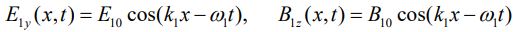
موج دوم نیز در جهت x- مطابق با رابطه زیر در حال حرکت است.

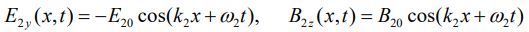
جهت سادگی، طول موج و دامنه این دو موج برابر در نظر گرفته شده. در حقیقت برای این دو موج داریم:

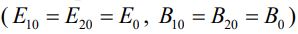
و

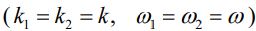
با استفاده از قانون جمع آثار میدان الکتریکی و مغناطیسی جدیدی را مطابق با دو رابطه زیر بدست می‌آوریم. در حقیقت در هرکدام از این روابط میدان‌های الکتریکی و مغناطیسی موج‌های رفت و برگشتی با هم جمع زده شده‌اند.

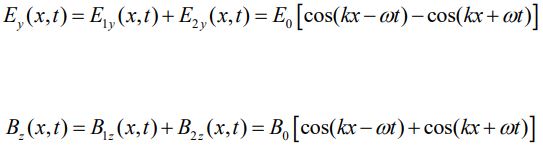
با استفاده از رابطه زیر در مثلثات:

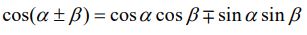
میدان الکتریکی و مغناطیسی جمع زده شده، به‌صورت زیر بازنویسی می‌شوند.

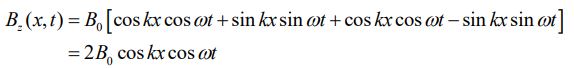
می‌توان نشان داد که دو میدان‌ بدست آمده در بالا نیز از رابطه کلی مربوط به امواج که در زیر آمده پیروی می‌کنند.

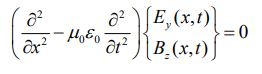
امواج مبتنی بر روابط ۱۲ و ۱۳ را موج‌های ایستا می‌نامند؛ دلیل این نامگذاری این است که امواج مذکور فقط با زمان نوسان می‌کنند و در راستای مشخصی منتشر نمی‌شوند. در حقیقت این امواج فقط با تغییرات زمان و مکان نوسان می‌کنند.

در ابتدا اجازه دهید تا میدان الکتریکی ارائه شده در رابطه ۱۲ را مورد بررسی قرار دهیم. با توجه به رابطه مذکور، بدیهی است که اگر sin kx=0 باشد، میدان الکتریکی در هر لحظه‌ای نیز صفر خواهد بود. در حقیقت در مکان‌های زیر، میدان الکتریکی در هر زمانی صفر است.

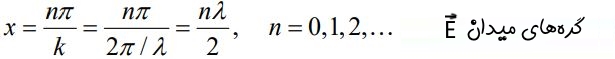
به نقاط بیان شده در بالا، نقاط گرهی گفته می‌شود. هم‌چنین به صفحاتی که در آن، گره‌ها قرار دارند، «صفحات گره» (Nodal planes) گفته می‌شود. در انیمیشنی که در زیر ارائه شده می‌توانید دو موج رفت و برگشتی که با یکدیگر جمع شده‌اند و موج ساکنِ اصلی را مشاهده کنید.

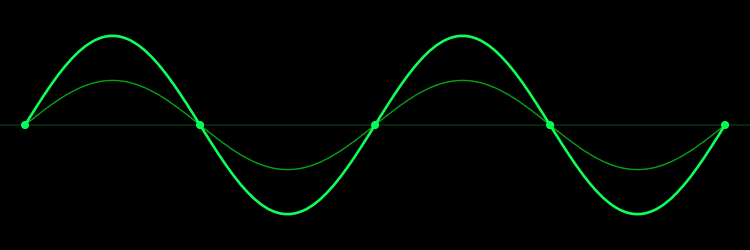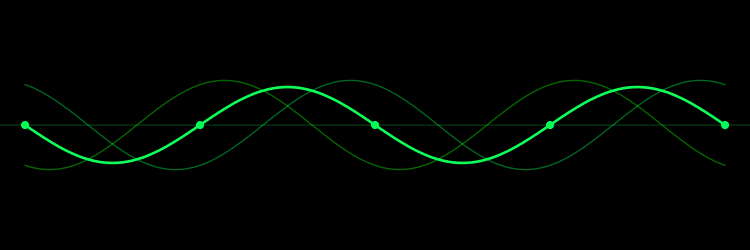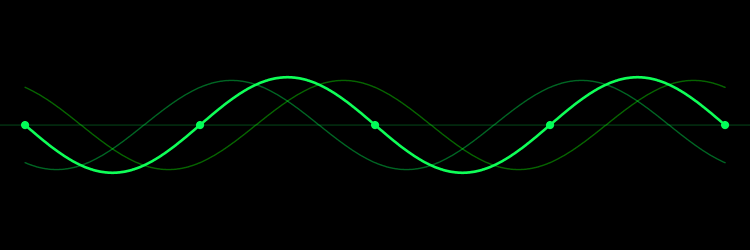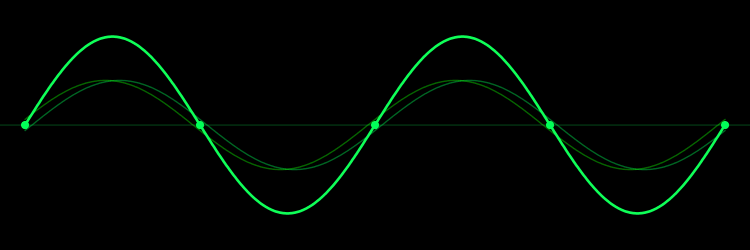
در انیمیشن بالا نقاط ساکن (گره‌ها) نیز، به صورت برجسته مشخص شده‌اند. در حالتی که sin kx=±1 باشد، یا به عبارتی دیگر در مکان‌های زیر:

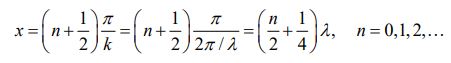
اندازه میدان الکتریکی به مقدار ماکزیممش (2E₀) رسیده. این نقاط در انیمیشن بالا قله‌های نوسان را نشان می‌دهند. برای میدان مغناطیسی نیز همین داستان برقرار است. نقاط گره برای میدان مغناطیسی، نقاطی‌اند که در آن‌ها Cos kx=۰ باشد. در نتیجه:

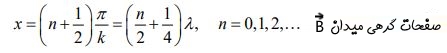
هم‌چنین نقاط مربوط به cos kx=±1 (نقاط قله) برابر هستند با:

بنابراین نقاط گرهی میدان الکتریکی، نقاط قله میدان مغناطیسی و نقاط گره میدان مغناطیسی معادل با نقاط قله میدان الکتریکی است. با توجه به رابطه ۱۲ اگر sin ωt=0 باشد، میدان الکتریکی نیز صفر است. در حقیقت در زمان‌های زیر، میدان الکتریکی صفر خواهد بود.

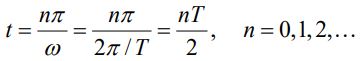
در رابطه بالا T=1/f=2π/ω را دوره (Period) می‌نامند. برعکس موج تخت در موج ایستا، میدان‌های الکتریکی و مغناطیسی نسبت به یکدیگر اختلاف فازی برابر با ۹۰ درجه دارند. شکل زیر موجی ایستا را نشان می‌دهد.

بردار پوئینتینگ (Poynting Vector)

در مطالب میدان الکتریکی و مغناطیسی دیدیم که یک میدان حامل انرژی است. از این رو با توجه به این‌که موج الکترومغناطیسی از دو میدان عمود به هم تشکیل شده، بنابراین این موج نیز حامل انرژی است. جهت بدست آوردن انرژی یک موج الکترومغناطیسی، مطابق با شکل زیر، دیفرانسیلی از موج به ضخامت dx و مساحت A را در نظر بگیرید.

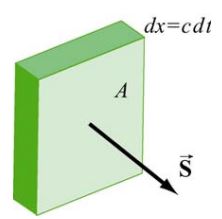
انرژی موجود در این دیفرانسیل برابر است با:

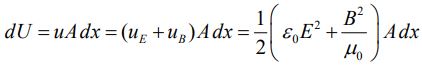
u_E و u_B به ترتیب نشان دهنده چگالی انرژی میدان الکتریکی و میدان مغناطیسی هستند، که با استفاده از رابطه زیر بدست می‌آیند.

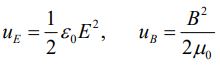
از آنجایی که امواج الکترومغناطیسی با سرعت نور منتشر می‌شوند، زمان مورد نیاز جهت جابجایی موج درون دیفرانسیل حجمی در نظر گرفته شده برابر با dt=dx/c است. نرخ انتقال انرژی در واحد سطح را با S نشان می‌دهند و مقدار آن با استفاده از رابطه زیر بدست می‌آید:

با توجه به رابطه بالا، واحد SI کمیتِ S برابر با W/m² است. با استفاده از روابط E=cB و $$c={\Large {1} \over \Large {\sqrt{\mu_0 \epsilon_0}}}$$ انرژی در واحد سطح را می‌توان به شکل زیر بازنویسی کرد.

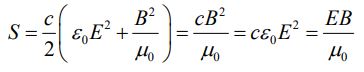
در حالتی عمومی، نرخ انرژی در واحد سطح را می‌توان با استفاده از کمیتی برداری تحت عنوان $$\overrightarrow {S}$$، به‌صورت زیر نشان داد.

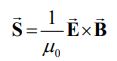
توجه داشته باشید که در رابطه بالا $$\overrightarrow{S}$$،‌ جهت انتشار را نشان می‌دهد. برای نمونه حالتی را فرض کنید که در آن $$\overrightarrow{E}=E_0cos(kx-\omega t) \widehat{j}$$ است. از این رو میدان مغناطیسی مرتبط با میدان الکتریکی بیان شده، بایستی برابر با $$\overrightarrow{B}=B_0cos(kx-\omega t) \widehat{k}$$ باشد. با فرض این‌که موج مفروض در راستای x+ انتشار می‌یابد، بردار پوئینتینگ برابر است با:

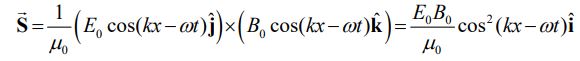
مطابق با شکل زیر بدیهی است که بردار $$\overrightarrow {S}$$ در راستای x+ است.

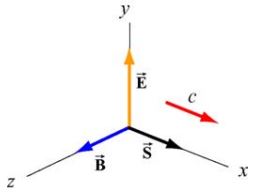
به انرژی در واحد سطح یک موج، «شدت موج» (Wave Intensity) گفته می‌شود. شدت موج کمیتی مقداری است که آن را با I نمایش می‌دهند. شدت موج در این مثال را می‌توان به‌صورت زیر محاسبه کرد.

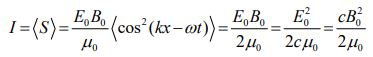
توجه داشته باشید که علامت <> در رابطه بالا نشان دهنده مقدار میانگین است. برای نمونه در رابطه بالا از مقدار میانگین ارائه شده در زیر استفاده شده است.

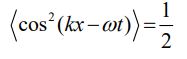
قبل از بیان ارتباط میان چگالی و شدت موج لازم است رابطه بین چگالی میدان الکتریکی و چگالی میدان مغناطیسی را به شکل زیر مشخص کنیم. این رابطه به‌صورت زیر است.

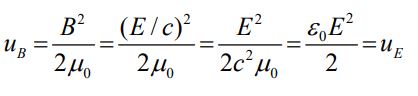
در نتیجه میانگین چگالی انرژیِ هر دو میدان برابر است با:

با توجه به رابطه ۱۴ و رابطه بالا ارتباط میان شدت و چگالی انرژی یک موج به‌صورت زیر بدست می‌آید.

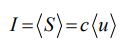
جهت درک بهتر، به مثال زیر توجه کنید.

مثال ۱: ثابت خورشیدی

در بالای سطح اتمسفر زمین، مقدار میانگینِ زمانی بردار پوئینتینگ، برابر با $$< S >=1.35×10^3 \enspace W/m^2$$ است. این مقدار تحت عنوان ثابت خوررشیدی شناخته می‌شود. با استفاده از ثابت خورشیدی، موارد زیر را بدست آورید.

1. با فرض این‌که موج الکترومغناطیسی ساطع شده از خورشید به صورت تخت باشد، اندازه دامنه میدان الکتریکی و مغناطیسی آن را بدست آورید.
2. اگر فاصله بین زمین و خورشید برابر با $$R=1.5×10^{11} \enspace m$$ باشد، انرژی میانگین زمانی ساطع شده از سطح خورشید چقدر است؟

(i): دامنه میدان الکتریکی منتشر شده برابر است با:

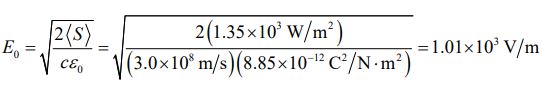
دامنه میدان مغناطیسی نیز برابر با مقدار زیر بدست می‌آید.

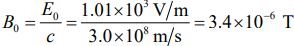
میدان مغناطیسی بدست آمده، تقریبا ۱۰ درصد میدان مغناطیسی زمین است.

(ii): میانگین انرژی زمانی ساطع شده از سطح خورشید، در فاصله R، برابر است با:

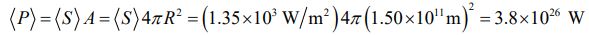
مثال بالا نمونه‌ای از موجی کروی است. منبع این‌گونه از امواج، یک نقطه است که نقش منتشر کننده میدان‌ها را دارند. در شکل زیر هر دو نوع موج کروی و تخت نشان داده شده است.

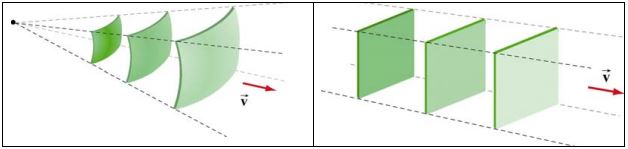
برای موجی کروی و در فاصله r از مرکز آن، شدت موج برابر با مقدار زیر است.

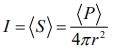
با توجه به ثابت بودن سطح یک موج تخت، بدیهی است که شدت انرژی برای آن، در هر فاصله‌ای ثابت است.

مثال ۲: شدت یک موج ایستا

موجی الکترومغناطیسی را مطابق با رابطه زیر در نظر بگیرید.

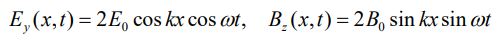
شدت این موج چقدر است؟

جهت بدست آوردن انرژی یک موج در ابتدا بایستی بردار پوئینتینگ را بدست آورد. بردار پوئینتینگ برای این مثال برابر است با:

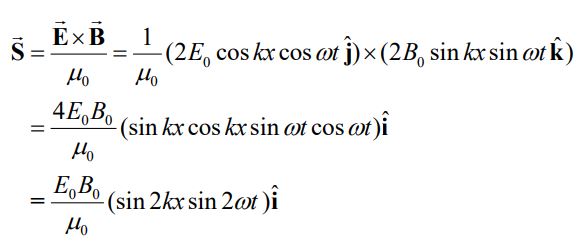
در نتیجه میانگین S برابر است با:

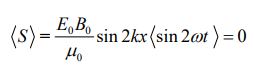
بنابراین انرژی خالصی توسط این موج منتقل نمی‌شود. در حقیقت رابطه بالا مربوط به موجی ساکن است. یا می‌توان گفت از آنجایی که موج ایستا در نتیجه برهم‌نهی دو موج با جهت حرکت مخالف است، بنابراین جابجایی انرژی خالصی توسط موج صورت نمی‌گیرد.

انتقال انرژی

با توجه به این‌که بردار پوئینتینگ $$\overrightarrow {S}$$ نشان دهنده نرخ انتقال انرژی در واحد مساحت است. در نتیجه نرخ تغییرات انرژی در واحد زمان را می‌توان مطابق با رابطه زیر بدست آورد.

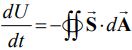
در رابطه بالا بردار مساحت برابر با $$d\overrightarrow {A}=dA \widehat{n}$$ و $$\widehat{n}$$ نشان دهنده بردار واحد به سمت بیرون از صفحه است. رابطه مذکور این اجازه را به ما می‌دهد تا بردار $$\overrightarrow {S}$$ را بر حسب شار چگالی انرژی بیان کنیم. اگر انرژی به سمت بیرون از سیستم جریان داشته باشد، $$\overrightarrow{S}=+S \widehat{n}$$ و dU/dt<0 است. این عبارت به معنی کاهش انرژی سیستم است.

جهت توضیح فیزیکی انرژی موج الکترومغناطیسی، مطابق با شکل زیر سلونوئیدی را در نظر بگیرید.

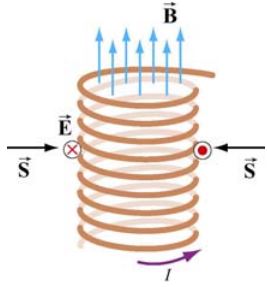
فرض کنید طول، شعاع و نسبت دور به طول برای این سلونوئید به‌ترتیب برابر با $$n, r, l$$ باشد. با فرض این‌که جریان الکتریکی با نرخ dI/dt>0 تغییر کند، قانون آمپر را می‌توان به شکل زیر نوشت:

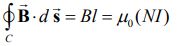
با توجه به تعریف n، رابطه بالا به شکل زیر قابل بازنویسی است.

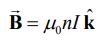
با مشتق‌گیری از آن، نرخ تغییرات میدان مغناطیسی نسبت به زمان برابر با مقدار زیر بدست می‌آید.

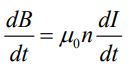
از طرفی با استفاده از قانون القای فارادی، داریم:

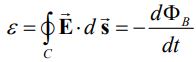
بدیهی است که تغییرات شار مغناطیسی، منجر به ایجاد میدان الکتریکی خواهد شد. با محاسبه انتگرال بالا داریم:

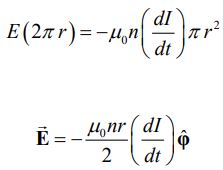
با استفاده از قانون لنز، جهت میدان الکتریکیِ $$\overrightarrow{E}$$ مطابق با شکل زیر، به‌صورت ساعتگرد بدست می‌آید.

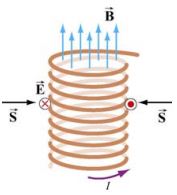
با بکارگیری میدان مغناطیسی و میدان الکتریکی بدست آمده، بردار پوئینتینگ به‌شکل زیر بدست می‌آید.

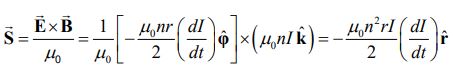
بردار بدست آمده به‌صورت شعاعی و رو به داخل است. در این مثال انرژی ذخیره شده در سلونوئید مفروض برابر است با:

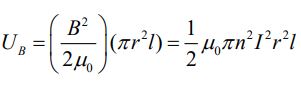
با مشتق‌گیری از رابطه بالا داریم:

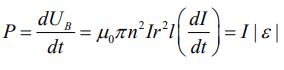
در رابطه بالا ε را با استفاده از القای فارادی و به شکل زیر بدست می‌آوریم.

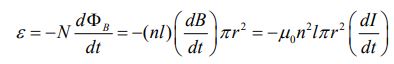
از طرفی با استفاده از مفهوم شدت موج، مقدار انرژی تولید شده در سلونوئید برابر است با:

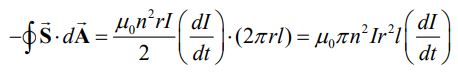
با توجه انرژی بدست آمده ناشی از ε و S، می‌توان رابطه زیر را نتیجه‌گیری کرد.

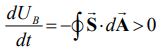
بنابراین همان‌طور که انتظار می‌رفت با افزایش جریان الکتریکی در زمان،‌ انرژی ذخیره شده در سلونوئید نیز افزایش می‌یابد.

ایجاد امواج الکترومغناطیسی

امواج الکترومغناطیسی زمانی ایجاد می‌شوند که بار‌های الکتریکی شتاب بگیرند. در حقیقت این بار‌های شتاب گرفته شده هستند که می‌توانند انرژی، تابش کنند. انرژی تابشی را نمی‌توان با استفاده از بار‌های ساکن یا جریان پایا بدست آورد. شکل زیر خطوط میدان الکتریکی را در نتیجه نوسان بار‌های الکتریکی، در یک لحظه خاص نشان می‌دهد.

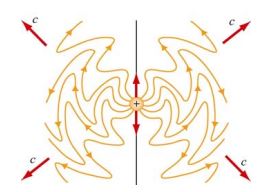
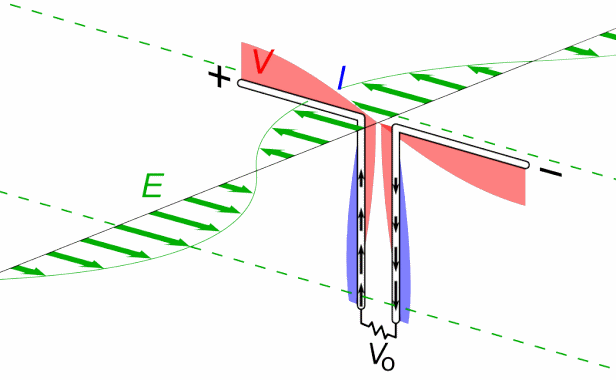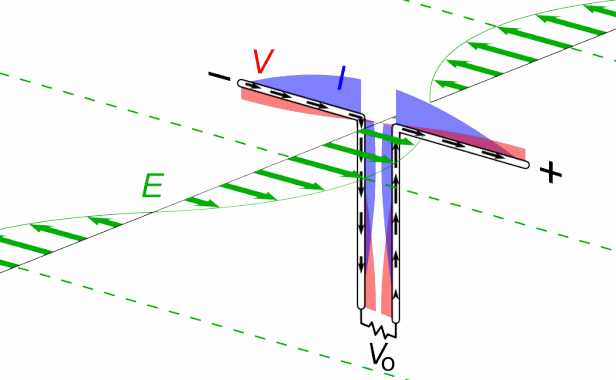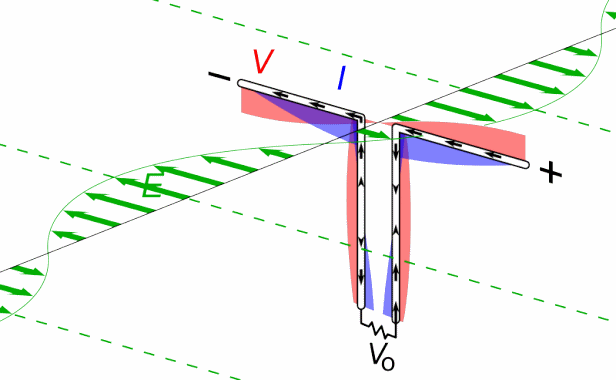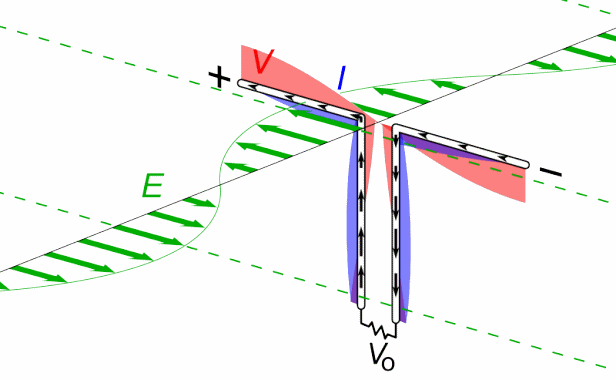
یکی از راه‌های شناخته شده تولید امواج الکترومغناطیسی (امواج رادیویی)، اعمال ولتاژی سینوسی به یک آنتن است. با انجام این کار، بار‌های الکتریکی به‌صورتی نوسانی در دو سمت آنتن جمع می‌شوند. در حقیقت یک دوقطبی الکتریکی نوسانی در هر لحظه ایجاد می‌شود که قدرت آن در هر لحظه تغییر می‌کند. در شکل زیر شماتیک تولید میدان الکتریکی سینوسی نشان داده شده.

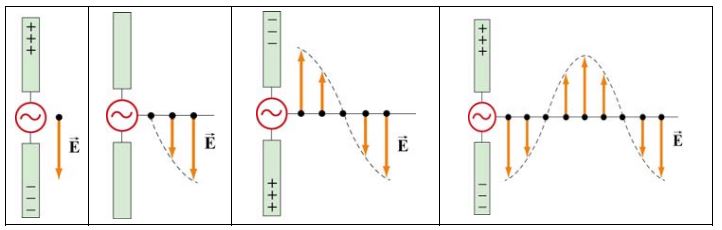
مطابق با شکل بالا در لحظه t=0 دو سمت آنتن بیشترین بار‌های الکتریکی مثبت و منفی را در خود دارند. در حقیقت بار بخش بالای آنتن، مثبت و بخش پایین منفی است. در این حالت میدان الکتریکی در نزدیکی آنتن به سمت پایین است. پس از گذشت مدت زمان ۱/۴ دوره، (t=T/4)، بارها به طور کامل جابجا شده و همدیگر را خنثی می‌کنند. در این حالت میدان الکتریکی در نزدیکی آنتن برابر با صفر است.

پس از گذشت زمان نصف دوره (t=T/2)، بار‌ها در حالتی برعکسِ لحظه t=0 قرار می‌گیرند. در حقیقت در این لحظه، اندازه میدان الکتریکی، ماکزیمم ولی جهت آن به سمت بالا می‌شود. بنابراین با گذشت زمان، نوسانات بار‌های الکتریکی منجر به تولید میدانی متغیر با زمان می‌شود. حرکت بار‌های الکتریکی هم‌چنین منجر به ایجاد جریان الکتریکی شده که نهایتا باعث تولید میدان مغناطیسی می‌شود. توجه داشته باشید که رفتار میدان‌ها در نزدیکی آنتن و در فاصله‌ای دور از آن با یکدیگر متفاوت است. انیمیشن زیر نحوه تولید میدان الکتریکی و مغناطیسی متغیر با زمان توسط آنتن را نشان می‌دهد.

مثال‌ها

مفاهیم مربوط به امواج الکترومغناطیسی پیش‌نیازی بسیار مهم برای دانشجویان مهندسی برق و خصوصا فیزیک است، چراکه در آینده در مباحث مهم‌تری همچون کوانتوم مکانیک، از آن‌ها استفاده خواهد شد. از این رو جهت تسلط کامل‌تر به موضوع، مطالعه مثال‌های زیر توصیه می‌شود. هم‌چنین جهت یادگیری کامل مفاهیم، آموزش ویدئویی ارائه شده در این قسمت به شما پیشنهاد می‌شود.

مثال ۳: موج الکترومغناطیسی تخت

فرض کنید میدان الکتریکی در یک موج الکترومغناطیسی مطابق با رابطه زیر تغییر می‌کند.

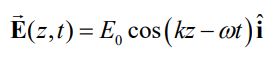
با این فرض،‌ مطلوب است:

1. جهت انتشار موج
2. میدان مغناطیسی مرتبط با میدان الکتریکی معرفی شده

(i): با نوشتن تابع درون کسینوس به صورت $$kz-\omega t=k(z-ct)$$، $$\omega$$ برابر با ck بدست می‌آید و جهت انتشار موج در جهت z+ تعیین می‌شود.

(ii): همان‌طور که در بالا نیز بیان شد، جهت انتشار موج الکترومغناطیسی برابر با جهت بردار پوئینتینگِ $$\overrightarrow{S}=(\overrightarrow{E}×\overrightarrow{B})/ \mu_0$$ است. علاوه بر این، با توجه به این‌که میدان $$\overrightarrow{B}$$ به میدان $$\overrightarrow{E}$$ و بردار $$\overrightarrow{S}$$ عمود است، بنابراین بردار میدان مغناطیسی $$\overrightarrow{B}$$ بایستی در جهت y، به صورت زیر باشد:

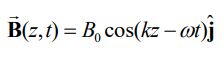
به‌منظور یافتن اندازه بردار $$\overrightarrow{B}$$ می‌توان از قانون القای فارادی به شکل زیر بهره برد.

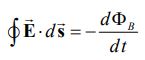
با ساده‌سازی رابطه بالا داریم:

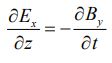
با جایگذاری E_x در رابطه بالا، اندازه میدان مغناطیسی، به شکل زیر بدست می‌آید:

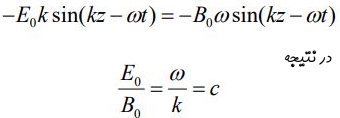
با بدست آمدن اندازه میدان مغناطیسی، شکل نهایی میدان بصورت زیر است.

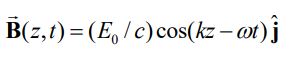
مثال ۴: معادله موج یک بعدی

ثابت کنید که به ازای ω=kc، میدان‌های زیر، امواجی یک‌ بعدی هستند.

همان‌طور که در بالا نیز بیان شد زمانی تابع (y(x,t، بیان کننده موج است که در معادله دیفرانسیل زیر صدق کند.

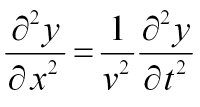
$$\nu$$ عددی ثابت است که در هر موجی مفهوم فیزیکی مشخصی را می‌رساند. در نتیجه جهت آزمودن میدان (E(x,t، آن را در رابطه بالا قرار می‌دهیم. با انجام این کار مشتقات اول و دوم مکانی میدان برابرند با:

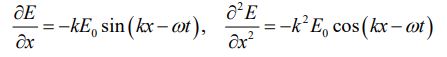
هم‌چنین مشتق اول و دوم زمانی میدان برابر هستند با:

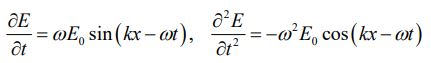
با جایگذاری مقادیر بدست آمده در معادله کلی موج داریم:

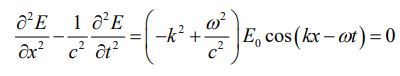
جهت برقرار بودن رابطه بالا بایستی ω=kc باشد. به طریقی مشابه می‌توان ثابت کرد که میدان مغناطیسی ارائه شده در این مثال نیز نوعی موج یک بعدی است.

مثال ۵: بردار پوئیتینگ

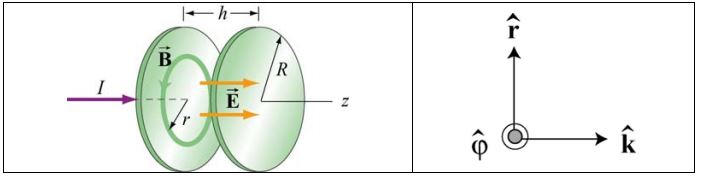
مطابق با شکل زیر خازنی را در نظر بگیرید که از دو صفحه به شعاع R ساخته شده که در فاصله h از یکدیگر قرار گرفته‌اند. این خازن با متصل شدن به جریان I با گذشت زمان شارژ می‌شود.

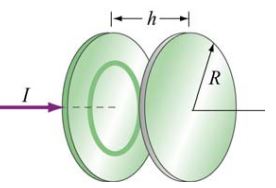
با توجه به فرضیات مسئله

• بردار پوئیتینگ $$(\overrightarrow{S})$$ را برای این خازن بیابید.
• با انتگرال‌گیری از S نشان دهید که نرخ انتقال انرژی به خازن برابر با نرخ ذخیره انرژی الکترواستاتیکی در خازن است.

(a): محور عبوری از دو صفحه خازن را در جهت z در نظر می‌گیریم. با فرض این‌که در یک لحظه خاص، بار روی صفحات برابر با Q باشد، میدان الکتریکی برابر خواهد شد با:

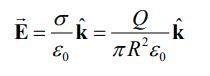
با توجه به رابطه آمپر-ماکسول، میدان مغناطیسی القا شده که ناشی از تغییر شار الکتریکی است را می‌توان با استفاده از رابطه زیر بدست آورد.

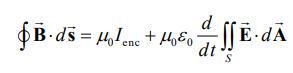
به‌دلیل تقارن استوانه‌ای سیستم، میدان مغناطیسی نیز به صورت شعاعی خواهد بود. در حقیقت میدان مغناطیسی را می‌توان به صورت $$\overrightarrow{B}=B \widehat{\phi}$$ نشان داد. در شکل زیر میدان الکتریکی و مغناطیسی شکل گرفته در سیستم، نشان داده شده است.

حلقه‌ای دایره‌ای شکل به شعاع r<R را میان دو صفحه خازن تصور کنید. با استفاده از رابطه آمپر-ماکسول ارائه شده، می‌توان نوشت:

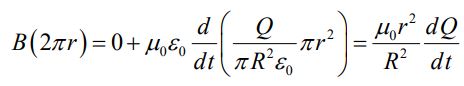
یا

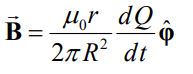
در نتیجه بردار پوئینتینگ $$\overrightarrow {S}$$ برابر است با:

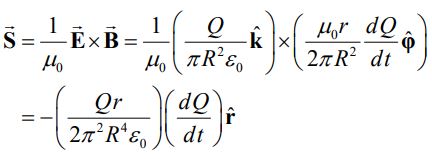
رابطه بالا جهت و اندازه بردار پوئینتینگ را نشان می‌دهند. این رابطه نشان می‌دهد که با افزایش Q در زمان، جهت این بردار به سمت داخل خازن (r-) است.

(b): در بخش میدان الکتریکی، به این نکته اشاره کردیم که چگالی انرژی الکتریکی ذخیره شده در میدان الکتریکی برابر با $$u_E=\epsilon_0E^2/2$$ است. در نتیجه کل انرژی ذخیره شده در میدان الکتریکی برابر خواهد بود با:

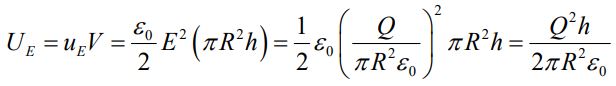
جهت بدست آوردن نرخ افزایش انرژی خازن، بایستی از رابطه بالا نسبت به زمان مشتق‌گیری کرد. در نتیجه داریم:

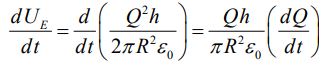
رابطه بالا مقدار انرژی ذخیره شده در خازن را با استفاده از مفهوم میدان الکتریکی به ما می‌دهد. با انتگرال‌گیری از این بردار روی سطح، نرخ انرژی وارد شده به خازن را می‌توان مطابق با رابطه زیر بدست آورد.

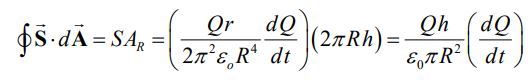
همان‌طور که می‌بینید نرخ انرژی وارد شده به سیستم برابر با نرخ انرژی ذخیره شده در میدان الکتریکی است.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه فیزیک و مهندسی برق، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس مهندسی برق
• مجموعه آموزش‌های مهندسی برق
• فیزیک الکتریسیته را به سادگی و با مجموعه مقالات وبلاگ فرادرس یاد بگیرید
• مجموعه آموزش‌های نرم‌افزار‌های مهندسی برق و الکترونیک
• مجموعه آموزش‌های فیزیک
• معادلات ماکسول (Maxwell’s Equations) — آموزش مفهومی