هامیلتونی – به زبان ساده

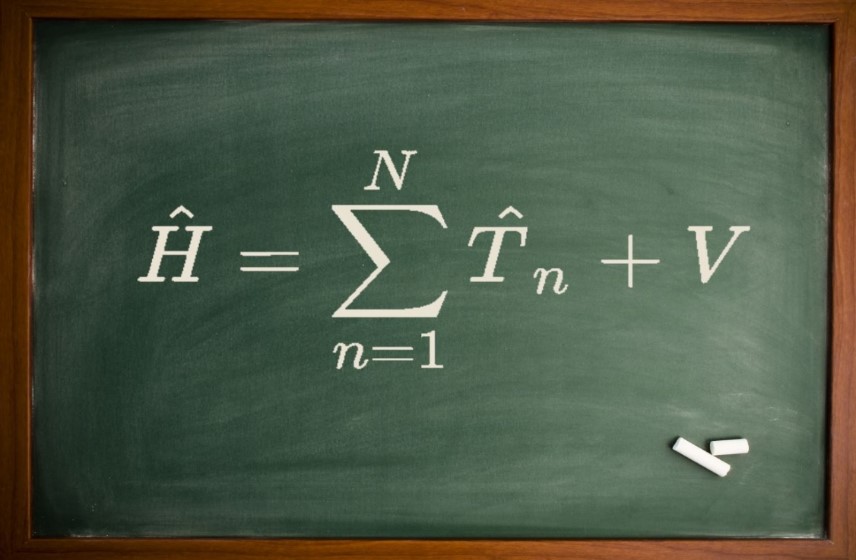
یکی از ستون‌های اصلی مکانیک کوانتومی، معادله شرودینگر است. این معادله توصیف کننده نحوه تغییر حالت کوانتومی یک سیستم با زمان است. در این معادله از اوپراتوری تحت عنوان هامیلتونی استفاده شده است. از این رو در این مطلب قصد داریم تا اوپراتور هامیلتونی را توضیح داده و مثال‌هایی از آن را در مکانیک کلاسیک ارائه دهیم. البته به منظور درک بهتر پیشنهاد می‌شود مطالب انرژی جنبشی و معادله اویلر لاگرانژ را مطالعه فرمایید.

هامیلتونی

در کوانتوم مکانیک، هامیلتونی، معادل با اوپراتوری است که با استفاده از آن مجموع انرژی‌های پتانسیل و جنبشی اندازه‌گیری می‌شود. معمولا هامیلتونی را با نماد‌های $$H , { } { \check { H } }$$ یا $$\hat { H }$$ نمایش می‌دهند. هامیلتونی برگرفته از اسم «ویلیام هامیلتون» (William Hamilton) است که علم مکانیک را متحول کرد.

فیلم آموزش مکانیک تحلیلی ۱ مرور و حل مثال در فرادرس

کلیک کنید

هامیلتونی معمولا به صورت مجموع اوپراتور‌هایی بیان می‌شوند که انرژی‌های جنبشی و پتانسیل سیستم را نمایندگی می‌کنند. در نتیجه اوپراتور هامیلتونی برابر است با:

$${ \displaystyle { \hat { H } } = { \hat { T } } + { \hat { V } } }$$

در رابطه فوق $$\hat { V }$$ نشان‌دهنده اوپراتور انرژی پتانسیل بوده و برابر است با:

$$\large { \displaystyle { \widehat { V } } = V = V ( \mathbf { r } , t ) }$$

هم‌چنین اوپراتور انرژی جنبشی نیز برابر است با:

$$\large { \displaystyle { \hat { T } } = { \frac { \mathbf { \widehat { p } } \cdot \mathbf { \widehat { p } } } { 2 m } } = { \frac { { \widehat { p } } ^ { 2 } } { 2 m } } = - { \frac { \hbar ^ { 2 } } { 2 m } } \nabla ^ { 2 } }$$

توجه داشته باشید که در رابطه فوق، $$m$$ نشان‌دهنده جرم ذره بوده و نقطه، نشان‌دهنده ضرب داخلی دو بردار است. هم‌چنین در این رابطه، اوپراتور تکانه برابر است با:

$$\large { \displaystyle { \hat { p } } = - i \hbar \nabla }$$

در رابطه بالا نیز $$\nabla$$، اوپراتور دل بوده و حاصل‌ضرب داخلی آن در خودش نیز برابر با $${ \displaystyle \nabla ^ { 2 } }$$ است که آن را لاپلاسین می‌نامند. رابطه مربوط به لاپلاسین در سه‌بعد مطابق با عبارت زیر است.

$$\large \nabla ^ { 2 } = { \frac { \partial ^ { 2 } } { { \partial x } ^ { 2 } } } + { \frac {\partial ^ { 2 } } { { \partial y } ^ { 2 } } } + { \frac {\partial ^ { 2 } } { { \partial z } ^ { 2 } } }$$

بیان بالا ممکن است الزاما از نظر فنی دقیق‌ترین تعریف فنی برای هامیلتونی نباشد. اما مرسوم‌ترین روش به‌ منظور بدست آوردن هامیلتونی محسوب می‌شود. با ترکیب اوپراتور‌های تعریف شده در بالا، نهایتا هامیلتونی را می‌توان مطابق با رابطه زیر بیان کرد:

$$\large {\displaystyle {\begin{aligned} { \widehat { H } } &= { \widehat {T}}+{ \hat { V } } \\ & = { \frac { \mathbf { \widehat { p } } \cdot \mathbf { \hat { p } } } { 2 m } }+V ( \mathbf {r} , t ) \\ & = - { \frac { \hbar ^ { 2 } }{ 2 m } } \nabla ^ { 2 } + V ( \mathbf { r } , t ) \end{aligned} } }$$

اوپراتور فوق روی تابع موجِ $${ \displaystyle \Psi ( \mathbf { r } , t ) }$$ که توصیف کننده سیستم است، اعمال می‌شود. معمولا این روش، فرمولاسیونی است که در تبیین معادله شرودینگر از آن استفاده می‌شود.

چند ذره

در حالتی که با سیستمی از چندین ذره سروکار داریم، هامیلتونی را می‌توان به صورت مجموع هامیلتونی تک‌تک ذرات تعریف کرد. بنابراین هامیلتونی برای سیستمی تشکیل شده از $$N$$ ذره برابر است با:

$$\large { \hat { H } } = \sum _ { n = 1 } ^ { N } { \hat { T } } _ { n } + V$$

در رابطه فوق $$V$$ نشان‌دهنده تابع پتانسیل ذرات بوده که وابسته به موقعیت‌های ذرات 1 تا $$N$$ است. بنابراین $$V$$ را می‌توان به صورت زیر بیان کرد:

$$\large {\displaystyle V = V ( \mathbf { r } _ { 1 } , \mathbf {r} _ { 2 } \cdots \mathbf { r } _ { N } , t ) }$$

به طور مشابه $$\widehat { T } _ n$$ نیز نشان‌دهنده اوپراتور انرژی جنبشی ذره $$n$$ بوده و رابطه آن به صورت زیر بدست می‌آید.

$$\large { \displaystyle { \hat { T } } _ { n } = { \frac {\mathbf { p } _ { n } \cdot \mathbf { p } _{ n } } { 2 m _ { n } } } }$$

هم‌چنین $${ \displaystyle \nabla _ { n } ^ { 2 } }$$، لاپلاسین ذره $$n$$ام را نشان می‌دهد و رابطه آن نیز به شکل زیر بدست می‌آید.

$$\large { \displaystyle \nabla _ { n } ^ { 2 } = { \frac { \partial ^ { 2 } } { \partial x _ { n } ^ {2 } } } + { \frac { \partial ^ { 2 } }{ \partial y _ { n } ^ { 2 } } } + { \frac { \partial ^ { 2 } } { \partial z _ { n} ^ { 2 } } } }$$

با استفاده از اوپراتور‌های فوق، شرودینگر-هامیلتونی، برابر با عبارت زیر بدست می‌آید.

$$\large { \displaystyle {\begin{aligned} { \hat { H } } & = \sum _ { n = 1} ^ { N } { \hat { T } }_ { n } + V \\ & = \sum _ { n = 1 } ^ { N } { \frac { \mathbf { \widehat { p } } _{ n } \cdot \mathbf {\widehat { p } } _ { n } } { 2 m _{ n } } }+ V ( \mathbf {r} _{1},\mathbf {r} _{2}\cdots \mathbf {r} _{N},t) \\ & = - { \frac { \hbar ^ { 2 } } { 2 } } \sum _{ n = 1 } ^ { N } { \frac { 1 } { m _{ n } } } \nabla _ { n } ^ { 2 }+V(\mathbf {r} _{1},\mathbf { r } _ { 2 } \cdots \mathbf { r } _ { N } ,t ) \end {aligned} } }$$

با توجه به این که پتانسیل سیستم وابسته به موقعیت فضایی ذرات نسبت به یکدیگر است، بنابراین انرژی جنبشی سیستم نیز به منظور ارضای پایستگی انرژی، به این موقعیت‌ها وابسته خواهد بود. از طرفی موقعیت ذره‌ها و نحوه حرکت آن‌ها نیز به یکدیگر وابسته است. از این رو ممکن در عبارت برآورد شده برای هامیلتونی، ضرایب خارجی نیز ظاهر شوند.

معادله شرودینگر

هامیلتونی، تغییر زمانی شرایط سیستم را برای ما توصیف می‌کند. در ابتدا فرض کنید $$\left | \psi ( t ) \right \rangle$$ نشان‌دهنده حالتِ سیستم در زمان $$t$$ باشد. در این صورت هامیلتونی این تابع برابر است با:

$$\large H \left | \psi ( t ) \right \rangle =i \hbar { \partial \over \partial t } \left | \psi ( t ) \right \rangle$$

عبارت فوق نشان‌دهنده معادله شرودینگر است. معادله فوق بیان می‌کند که اگر وضعیت سیستم در زمانِ $$t$$ معلوم باشد، در این صورت می‌توان از وضعیت سیستم در زمان $$t + \delta t$$ آگاه بود. در حالتی خاص که $$H$$ وابسته به زمان نباشد، معادله فوق را می‌توان به صورت زیر بازنویسی کرد.

$$\large \left | \psi ( t ) \right \rangle =e ^ { - i H t / \hbar } \left|\psi ( 0 ) \right \rangle$$

اوپراتور نمایی نشان داده شده در سمت راست معادله شرودینگر معمولا با استفاده از سری توانی بر حسب $$H$$ نشان داده می‌شود. توجه داشته باشید که در این مطلب تنها مقدماتی از کوانتوم مکانیک توضیح داده شده و در مطالب آینده به طور اختصاصی به این مقوله خواهیم پرداخت.

هامیلتونی در حالت‌های مختلف

در ادامه، به منظور درک بهتر مفهوم هامیلتونی، این اوپراتور را در چندین حالت مختلف بدست آورده‌ایم. توجه داشته باشید که در روابط ارائه شده در ادامه، بار الکتریکی با نماد $$q$$ و جرم با $$m$$ نشان داده شده‌اند.

ذره آزاد

ذره‌ای را در نظر بگیرید که هیچ پتانسیلی نداشته باشد. در حقیقت پتانسیل برای این ذره برابر با صفر بوده در نتیجه هامیلتونی را برای آن می‌توان به صورت زیر بیان کرد:

$$\large { \hat { H } } = - { \frac {\hbar ^ { 2} }{ 2 m } } { \frac { \partial ^ { 2 } } { \partial x ^ { 2 } } }$$

اوپراتور بالا در حالت تک‌بعدی بیان شده است. در حقیقت شکل سه‌بعدی اوپراتور فوق را می‌توان به صورت زیر بیان کرد:

$$\large { \hat { H } } = - { \frac { \hbar ^ { 2 } } { 2 m } } \nabla ^ { 2 }$$

پتانسیل ثابت

برای ذره قرار گرفته در فضایی با پتانسیل ثابتِ $${ \displaystyle V = V _ { 0 } }$$، هامیلتونی برابر است با:

$$\large { \hat { H } } = - { \frac { \hbar ^ { 2 } } { 2 m } } { \frac { \partial ^ { 2 } } { \partial x ^ { 2 } } } + V _ { 0 }$$

شکل سه‌بعدی عبارت فوق نیز به صورت زیر بیان می‌شود.

$$\large { \hat { H } } = - { \frac { \hbar ^ { 2 } } { 2 m } } \nabla ^ { 2 } + V _ { 0 }$$

معادله فوق به مسائلی اطلاق می‌شود که در اصطلاح به آن‌ها ذره در جعبه گفته می‌شود.

نوسانگر ساده

برای یک نوسانگر ساده که در یک بُعد قرار گرفته، پتانسیل با توجه به موقعیت تغییر می‌کند. در این شرایط پتانسیل ذره برابر است با:

$$\large V = { \frac { k } {2 } } x ^{ 2 } = { \frac { m \omega ^ { 2 } } { 2 } } x ^ { 2 }$$

در رابطه فوق $$\omega$$، نشان‌دهنده فرکانس زاویه‌ای، $$k$$، ثابت فنر و $$m$$ جرم نوسان‌گر است. البته سرعت زاویه‌ای و سختی فنر را می‌توان با یکدیگر و همان‌طور که در ادامه نشان داده شده، معادل‌سازی نیز کرد.

$$\large \omega ^ { 2 } = { \frac { k } { m } }$$

بنابراین هامیلتونی نیز برابر است با:

$$\large { \hat { H } } = - { \frac { \hbar ^ { 2 } }{ 2 m } } { \frac { \partial ^ { 2 } } { \partial x ^ { 2 } } } + { \frac { m \omega ^ { 2 } } { 2 } } x ^ { 2 }$$

اوپراتور فوق در حالت سه‌بعدی نیز به صورت زیر بدست می‌آید.

$$\large { \hat { H } } = - { \frac { \hbar ^ { 2 } } { 2 m } } \nabla ^ { 2 } + { \frac { m \omega ^ { 2 } } { 2 } } r ^ { 2 }$$

ترمِ $$r ^ 2$$ در عبارت فوق اسکالر بوده و اندازه آن برابر است با:

$$\large { \displaystyle r ^ { 2 } = \mathbf { r } \cdot \mathbf {r} =|\mathbf { r } |^ { 2 } = x ^ { 2 } + y ^ { 2 } + z ^ { 2 } }$$

نهایتا با جمع هامیلتونی در هر سه جهت، داریم:

$$\large { \begin {aligned} { \hat { H } } & = - { \frac { \hbar ^ { 2 } } { 2 m } } \left ( { \frac { \partial ^ { 2 } } { \partial x ^ { 2 } } } + { \frac { \partial ^ { 2 } } { \partial y ^ { 2 } } } + { \frac { \partial ^ { 2 } } { \partial z ^ { 2 } }} \right ) + { \frac { m \omega ^ { 2 } } { 2 } } ( x ^ { 2 } + y ^ { 2 } + z ^ { 2 } ) \\& = \left(-{\frac {\hbar ^ { 2 }} { 2 m } } { \frac {\partial ^{2}}{\partial x ^ { 2 } } } + { \frac { m \omega ^{ 2 } }{2} } x ^ {2 } \right)+\left(-{\frac {\hbar ^ { 2 } } {2 m } } { \frac {\partial ^{2}}{ \partial y ^ { 2} } } + { \frac {m\omega ^ { 2 } }{ 2 } }y ^ { 2 } \right ) + \left(-{\frac { \hbar ^{ 2 } } { 2m } } { \frac {\partial ^ { 2 } } { \partial z^ { 2 } } } + { \frac {m\omega ^ { 2} }{ 2 } } z ^ { 2 } \right ) \\\end {aligned} }$$

موتور صلب

برای یک موتور صلب، برای نمونه سیستمی از ذرات که حول محوری ثابت دوران می‌کنند، هامیلتونی برابر است با:

$$\large { \hat { H } } = - { \frac { \hbar ^ { 2 } } { 2 I _ { x x } } } { \hat { J } } _ { x } ^ { 2 } - { \frac { \hbar ^ { 2 } } {2 I _ { y y } } } { \hat { J } } _ { y } ^ { 2 } - { \frac { \hbar ^ { 2 } } { 2 I _ { z z } } } { \hat { J } } _ { z } ^ { 2 }$$

در رابطه فوق، $$I _ { x x }$$، $$I _ { y y }$$ مولفه‌های گشتاور اینرسی و $${ \displaystyle { \hat { J } } _ { x } \, \! }$$ و $${ \displaystyle { \hat { J } } _ { y } \, \! }$$ مولفه‌های گشتاور قطبی حول محور‌های $$x$$ و $$y$$ است.

پتانسیل کولمب یا الکترواستاتیک

در مطلب پتانسیل الکتریکی بیان شد که پتانسیل الکتریکی ایجاد شده در نتیجه قرار گرفتن دو بار نقطه‌ای $$q _ 1$$ و $$q _ 2$$ در فاصله $$r$$، مقدار پتانسیل ایجاد شده برابر است با:

$$\large { \displaystyle V = { \frac { q _ { 1 } q_ { 2 } }{ 4 \pi \epsilon _ { 0 } |\mathbf { r } |} } }$$

با این حال مقدار فوق برابر با پتانسیل یک بار در نتیجه بار دیگر است. در حقیقت اگر $$N$$ ذره در کنار یکدیگر قرار گیرند، هر ذره نسبت به دیگر ذرات دارای پتانسیل خواهد بود. برای $$N$$ ذره پتانسیل الکتریکیِ $$q _ j$$ در نتیجه دیگر ذرات برابر است با:

$$\large V _ { j } = { \frac { 1 } { 2 } } \sum _ { i \neq j } q _ { i } \phi ( \mathbf { r } _ { i } ) = { \frac { 1 } { 8 \pi \varepsilon _ { 0 } } } \sum _ { i \neq j } { \frac { q _ { i } q _ { j } } { |\mathbf { r } _ { i } - \mathbf { r } _ { j } |} }$$

در رابطه بالا $${ \displaystyle \phi ( \mathbf { r } _ { i } ) }$$ نشان‌دهنده پتانسیل الکترواستاتیکی ناشی از بار $$q _ j$$ است که در فاصله $$r _ i$$ قرار گرفته است. در نتیجه نهایتا پتانسیل کلی سیستمی با $$N$$ بار الکتریکی برابر است با:

$$\large V = { \frac { 1 } { 8 \pi \varepsilon _ { 0 } } } \sum _ { j = 1 } ^ { N } \sum _ { i \neq j } { \frac { q _ { i } q _ { j } } { |\mathbf { r } _ { i } - \mathbf { r } _ { j } |} }$$

بنابراین هامیلتونی برای چنین سیستمی برابر است با:

$$\large { \begin {aligned} { \hat { H } } & = - { \frac {\hbar ^{2}}{ 2 } } \sum _ { j= 1} ^ { N } { \frac {1}{m_{j}}}\nabla _{j}^{2}+{\frac { 1 } { 8 \pi \varepsilon _ { 0 } } } \sum _{j=1}^{N}\sum _{ i \neq j } { \frac { q _ { i } q _{ j } } {|\mathbf {r} _{i}-\mathbf {r} _ { j } | } } \\ & = \sum _ { j =1 } ^ { N } \left(-{\frac {\hbar ^{ 2 }} { 2 m_ { j} } } \nabla _{ j } ^{ 2 } +{ \frac { 1 } { 8\pi \varepsilon _{0 } } } \sum _ { i \neq j}{\frac {q _ { i } q _ { j } } { |\mathbf {r} _{i}-\mathbf { r } _ { j } |} } \right ) \\\end {aligned}}$$

هامیلتونی مفهومی پرکاربرد در فیزیک بوده که در بدست آوردن بسیاری از معادلات فیزیکی کاربرد دارد. البته در آینده بیشتر در مورد این عملگر بحث خواهیم کرد.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه فیزیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• معادله اویلر لاگرانژ -- به زبان ساده
• عدم قطعیت هایزنبرگ — به زبان ساده
• سیاه چاله چیست؟ — به زبان ساده

^^