محلول ایده آل — به زبان ساده

در محلول ایده آل شامل A و B، برهمکنشهای A-B همانند برهمکنشهای A-A و B-B هستند. در چنین شرایطی، رابطه بین غلظت محلول و فشار جزئی فاز گاز برای هر جزء به کمک قانون رائول بیان میشود. در یک محلول ایدهآل، بخار بالای محلول، غنی از اجزای فرار است که به کمک تقطیر جز به جز، این اجزا جداسازی میشوند. اجزای حلشونده غیرفرار، موجب کاهش فشار بخار بالای محلول میشوند. چنین محلولهایی با کاهش نقطه انجماد و افزایش نقطه جوش همراه هستند. این خواص، در یک محلول ایده آل تنها به غلظت وابستهاند و وابستگی به نوع حلشونده فرار ندارند. محلول ایده آل را به کمک اصلاح مدل محلول ایده آل رقیق توصیف میکنند. در یک محلول ایده آل رقیق، حلال از قانون رائول و حلشونده از قانون هنری پیروی میکنند. چنین قانونی با محدودیتهایی برای اجرا روبرو است.
برای تعیین مقدار انحراف از مدل محلول ایده آل رقیق، مفهومی به نام «اکتیویته» (Activity) یا فعالیت معرفی میشود. اکتیویته یک جزء از محلول را بر اساس حالت استاندارد بیان میکنند. دانستن اکتیویته اجزای واکنشپذیر یک مخلوط، برای مدل کردن تعادل شیمیایی، اهمیت بالایی دارد. ثابت تعادل ترمودینامیکی برای یک واکنش در محلول به کمک تعریف خارج قسمت واکنش و بر اساس اکتیویته تعریف میشود که در حالت کلی، آنرا بر اساس غلظت بیان میکردیم.
تعریف محلول ایده آل
در یک گاز ایدهآل، اتمها یا مولکولها با یکدیگر برهمکنشی ندارند. به طور مشخص، چنین مدلی برای یک مایع مناسب نیست زیرا یک گاز، بدون برهمکنشهای جاذب، متراکم نخواهد شد. تفاوت نقطه جوش عناصر، حاکی از تفاوت زیاد برهمکنشهای جاذب در مایعات است. به طور مثال، نقطه جوش هلیوم برابر با 4/2 کلوین ذکر میشود در حالیکه هافنیوم، نقطه جوشی معادل 5400 کلوین دارد.
در توسعه مدلی برای محلولها، فاز بخار در تعادل با محلول نیز باید لحاظ شود. بنزن خالص مایعی را در نظر بگیرید که در یک بشر و در اتاقی بسته قرار دارد. از آنجایی که مایع، با فاز بخار بالای خود در تعادل است، فشار جزئی غیر صفر از بنزن در محیط اطراف بشر وجود دارد. این فشار موسوم به فشار بخار بنزن در دمای مایع است. حال اگر به بشر، تولوئن اضافه کنیم چه اتفاقی میافتد؟ مشاهده میشود که فشار جزئی بنزن، کاهش مییابد. برای چنین مخلوطی، فشار جزئی جزء i در بالای مایع، با رابطه زیر بیان میشود که در آن، $$x_i$$ کسر مولی جزء در مایع است.
$$\begin {equation} P _{i} =x _{i} P_{i} ^ {*} \quad i = 1, 2 \end {equation}$$
این رابطه بیان میکند که فشار جزئی هریک از اجزا به طور مستقیم با فشار بخار متناظر با مایع خالص $$(P _ i ^ \star)$$ تناسب دارد و این ثابت تناسب، همان کسر مولی است. رابطه بالا را با نام قانون رائول میشناسند و در حقیقت، تعریف یک محلول ایده آل به شمار میآید. در محلولهای دوجزئی (باینری)، جزئی که $$x_i$$ بیشتری داشته باشد، حلال و جزئی که $$x_i$$ کمتری داشته باشد، حلشونده نام دارد. محلولهای کمی هستند که از قانون رائول پیروی میکنند اما مطالعه آنها برای بررسی انحراف از رفتار ایدهآل اهمیت دارد.
رابطه بالا تنها زمانی کاربرد دارد که برهمکنشهای A-A ،A-B و B-B همگی با یکدیگر برابر باشند. این معیار برای مخلوط بنزن و تولوئن صدق میکند زیرا مولکولهای این دو ماده از نظر اندازه، شکل و خواص شیمیایی، مشابه یکدیگرند اما این قانون برای تمامی محلولها صدق نمیکند و با محدودیتهایی روبرو است. حلال در یک محلول ایده آل زمانی از قانون رائول پیروی میکند که بسیار رقیق شده باشد.
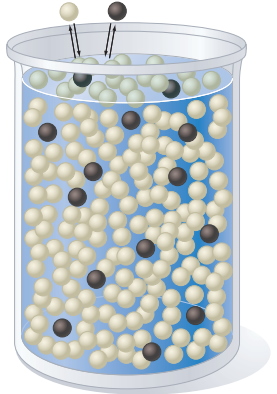
در مثال زیر سعی میکنیم قانون رائول را اثبات کنیم. در محلول، مولکولهای حلشونده در حلال توزیع شدهاند. این محلول در تعادل با فاز گاز قرار دارد و ترکیب فاز گاز نیز به کمک تعادل دینامیکی بین تبخیر و میعان تعیین میشود که در تصویر بالایی، شمایی از آن نمایش داد شده است.
مثال برای اثبات قانون رائول
فرض کنید که سرعت تبخیر $$(R _ { evap})$$ و سرعت میعان $$(R _ { cond})$$ حلال در سطح مایع خالص حلال، به صورت زیر تعریف شده باشند. در این رابطه، A مساحت سطح مایع و k نیز ثابتهای سرعت برای تبخیر و میعان هستند. رابطهای بین فشار بخار حلال، بالای محلول و بالای حلال خالص بیابید.
$$\begin {equation} \begin {array} {l}
R _ {\text {evap}} = A k_ {\text {evap}} \\
R_ {\text {cond}}= A k _{\text {cond}} P_{\text {solvent}} ^{*}
\end {array} \end {equation}$$
برای حلال خالص، فشار بخار تعادلی با برابر گرفتن نرخ تبخیر و میعان محاسبه میشود:
$$\begin {equation} \begin {aligned}
R _ {\text {evap}} & = R_ {\text {cond}} \\
A k _{\text {evap}} & = A k_ {\text {cond}} P_{\text {solvent}}^ {*} \\
P_ {\text {solvent}} ^{*} &= \frac { k_{\text {evap}}} {k _{\text {cond}}}
\end {aligned} \end {equation}$$
سپس یک محلول ایده آل را در نظر بگیرید. در این حالت، نرخ تبخیر با عامل کسر مولی کاهش پیدا میکند زیرا تنها کسری از سطح برای تبخیر حلال در دسترس خواهد بود.
$$\begin{equation} \begin {array} {l}
R _ {\text {evap} } = A k _ {\text {evap} } x _{\text {solvent}} \\
R _{\text {cond}} = A k_ {\text {cond}} P _{\text {solvent}}
\end {array}\end {equation}$$
در حالت تعادلی خواهیم داشت:
$$\begin {equation} \begin {aligned}
R _ {\text {evap}} & =R _{\text {cond}} \\
A k_{\text {evap}} x _{\text {solvent}} & =A k _ {\text {cond}} P _{\text {solvent}} \\
P _{\text {solvent}} & =\frac {k _ {\text {evap}}} { k_ {\text {cond}}} x _ {\text {solvent}} = P _ {\text {solvent}} ^ {*} x _{\text {solvent}}
\end{aligned}\end{equation}$$
رابطه بدست آمده، همان قانون رائول است.
پتانسیل شیمیایی در فازهای گاز و محلول
اگر فازهای مایع و بخار در حال تعادل باشند، رابطه زیر برای هر جزء از محلول برقرار است. در این رابطه، $$\mu _ i$$، پتانسیل شیمیایی جزء i به شمار میآید. پتانسیل شیمیایی یک ماده در فاز گاز، با فشار جزئی آن طبق رابطه زیر مرتبط میشود:
$$\begin {equation} \mu _ {i} ^ {\text {vapor} } = \mu _{ i}^ {\circ} + R T \ln \frac {P _{i}} { P ^ {\circ}} \end {equation}$$
در این رابطه، $$\mu _{ i}^ {\circ}$$، پتانسیل شیمیایی برای جزء خالص i در فاز گاز در فشار استاندارد $$1 bar$$ است. با توجه به اینکه در هنگام تعادل، پتانسیل محلول و بخار با یکدیگر برابرند، رابطه فوق را میتوان به شکل زیر نوشت:
$$\begin {equation} \mu _ {i} ^ {\text {solution}} = \mu _ {i}^ {\circ} + R T \ln \frac { P_{i }} { P ^{\circ}} \end {equation}$$
برای یک مایع خالص که در تعادل با بخار قرار دارد، رابطه زیر برقرار است:
$$\mu _ {i}^ {\star}$$ = (بخار) $$\mu _ {i}^ {\star}$$ = (مایع) $$\mu _ {i}^ {\star}$$
بنابراین، پتانسیل شیمیایی مایع خالص به کمک رابطه زیر بیان میشود:
$$\begin {equation}\mu _ {i } ^ {*} = \mu _{ i} ^ { \circ} + R T \ln \frac { P _ { i } ^{ * } } { P ^ {\circ}} \end {equation}$$
با کم کردن دو رابطه بالا از یکدیگر، به رابطه زیر برای پتانسیل محلول میرسیم:
$$\begin{equation} \mu _ {i} ^ {\text {solution}} = \mu _ { i } ^ {*} + R T \ln \frac { P_{i}} { P_{i} ^ {*}} \end {equation}$$
با ترکیب رابطه بالا و قانون رائول که در ابتدای آموزش مطرح کردیم، به رابطه اصلی در محلول ایده آل میرسیم:
$$\begin {equation} \mu _ { i } ^ { \text {solution} } = \mu_{i}^ { *} + R T \ln x _ { i } \end {equation}$$
این رابطه، پتانسیل شیمیایی یک جزء در یک محلول ایده آل را به پتانسیل شیمیایی مایع خالص جزء i و کسر مولی آن جزء در محلول مرتبط میکند. این رابطه در توصیف ترمودینامیک محلولهایی کاربرد دارد که در آنها، تمامی اجزا در همه نسبتها، فرار و امتزاج پذیر هستند. شکل رابطه بالا مشابه رابطه انرژی گیبس برای مخلوطها است. در نتیجه میتوان رابطهای برای ترمودینامیک مخلوط در محلولهای ایدهآل تعریف کنیم. برای یک محلول ایده آل خواهیم داشت:
$$\Delta H _ {mixing} = \Delta V _ {mixing} = 0$$
$$\Delta G _ {m i x i n g} = n R T \sum _ { i } x _ { i } \ln x_{i} \\
\Delta S _ {\text {mixing}} = -\left(\frac{\partial \Delta G _ {\text {mixing}}} {\partial T } \right ) _ {P, n_{1}, n_{2} } = -n R \sum _ { i } x _ { i } \ln x _ {i}\\
\begin {aligned}
\Delta V _ {\text {mixing} } & = \left ( \frac { \partial \Delta G _ {\text {mixing }}}{\partial P}\right)_{T, n_{1}, n_{2}}=0 \quad \text { } \\
\Delta H_{\text {mixing}} &= \Delta G _ {\text {mixing}} + T \Delta S _ {\text {mixing}} \\
&=n R T \sum x _{i} \ln x_ { i } - T \left ( n R \sum x _ { i } \ln x _ { i } \right ) = 0
\end {aligned}$$
مثال برای محاسبه انرژی گیبس در محلول ایده آل
محلولی ایدهآل از ۵ مول بنزن و 3/25 مول تولوئن ساخته شده است. میزان $$\Delta G _ {\text {mixing }}$$ و $$\Delta S _ {\text {mixing }}$$ را در فشار $$1bar$$ و دمای 298 کلوین محاسبه کنید.
در ابتدا، کسرهای مولی را حساب میکنیم که برای بنزن و تولوئن به ترتیب برابر با 0/606 و 0/394 هستند.
$$\begin {aligned}
\Delta G _ {\text {mixing}} &= n R T \sum_{i} x _{i} \ln x _{i} \\
&=8.25 \mathrm {mol} \times 8.314 \mathrm { J } \mathrm {mol} ^ {-1} \mathrm {K} ^ {-1} \\
& \times 298 \mathrm {K} \times(0.606 \mathrm {ln} 0.606 + 0.394 \ln 0.394) \\
& = -13.7 \times 10 ^ { 3 } \mathrm { J } \\
\Delta S _ {\text {mixing }} & = - n R \sum _ {i} x _ {i} \ln x _ { i} \\
&=-8.25 \mathrm {mol} \times 8.314 \mathrm {Jmol} ^ {-1} \mathrm { K} ^ { -1} \times (0.606 \ln 0.606+0.394 \ln 0.394) \\
&=46.0 \mathrm { JK} ^ {-1}
\end {aligned}$$
با توجه به اینکه مقدار $$\Delta G _ {\text {mixing }}$$ منفی شد، فرآیند اختلاط، خود به خودی خواهد بود. اگر دو مایع، امتزاجپذیر باشند، همواره $$\Delta G _ {\text {mixing }}$$ عددی منفی خواهد بود.
مدل محلول ایده آل در محلولهای دوجزئی
با وجود اینکه مدل محلول ایده آل را میتوان در مورد محلولهای چندجزئی هم بکار برد اما برای سادهسازی محاسبات ریاضی، در این مطلب از محلولهای دوجزئی استفاده میکنیم. با توجه به اینکه قانون رائول در هر دو جزء مخلوط صدق میکند، فشار کلی در فاز گاز، با کسر مولی هر جزء در مایع به طور خطی تغییر میکند. رابطه فشار کل در زیر آورده شده است:
$$P _ {\text {total} } = P _{1} +P_{2}= x_{1} P_{1}^{*}+ \left(1-x _{1}\right) P_{2} ^{*}= P_{2}^{*} +\left (P_{1}^{*}- P_{2}^{*} \right) x _{1}$$
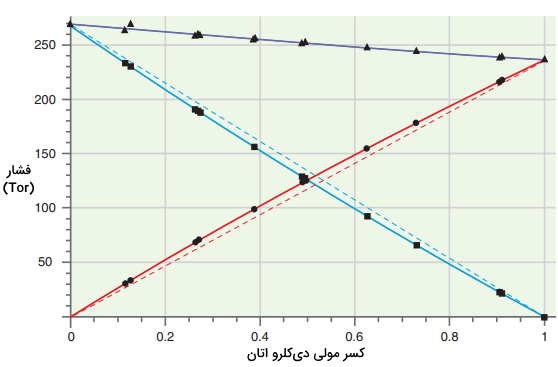
فشارهای جزئی و فشار کل بالای محلول بنزن و 1و۲ دیکلرواتان با فرمول $$C_2 H _ 4 Cl_2$$ در تصویر زیر نشان داده شده است. در این تصویر، انحرافات کمی از قانون رائول را مشاهده میکنید. این انحرافات به طور معمول اتفاق میافتند چراکه محلولهای کمی هستند که به طور کامل از قانون رائول پیروی میکنند. انحرافات بسیار زیاد در قانون رائول، محلولهای غیرایدهآل را بوجود خواهد آورد.
در رابطه بالا، کسر مولی هر جزء در فاز گاز را هم میتوان محاسبه کرد. با استفاده از تعریف فشار جزئی و نماد $$y$$ برای کسر مولی در فاز گاز، خواهیم داشت:
$$y _ {1} = \frac{P_{1}} {P_{\text {total}}} = \frac { x _ { 1 } P _ { 1 } ^ { * } } { P _ { 2 } ^ { *} + \left ( P _ { 1 } ^ {*} -P _{2}^{*}\right) x_{1}}$$
برای بدست آوردن فشار در فاز بخار به صورت تابعی از $$y_1$$، در ابتدا، رابطه بالا را برای $$x_1$$ حل میکنیم.
$$x _ {1} = \frac {y_{1} P_ {2} ^ {*} } {P _ { 1 } ^ {* } + \left ( P _ { 2 } ^ { * } - P _ { 1 } ^ { * } \right ) y _ { 1 } }$$
با توجه به رابطه $$ P _ {total} = P ^\star _ 2+ (P ^\star _ 1 - P ^\star _ 2)x_1$$ خواهیم داشت:
$$P _ { \text {total}} = \frac { P _ { 1 } ^ { * } P _ { 2} ^{ * } } { P _ { 1 } ^ { * } + \left ( P _ { 2 } ^ { * } - P _ { 1 } ^ { * } \right ) y _ { 1 } }$$
رابطه بالا را میتوان برای $$y_1$$ بازآرایی کرد تا رابطهای بر حسب فشار بخار جزء خالص و فشار کل بدست آید.
$$y _ { 1 } = \frac { P _ {1}^{*} P _{\text {total}}- P _{1}^ {*} P _{2}^{*}} { P_ {\text {total}} \left (P_{1} ^{*}- P_{2}^ {*} \right)}$$
تغییرات فشار کل با $$x_1$$ و $$y_1$$ همانند تصویر قبل نیست. در تصاویر زیر، فشار کل بالای محلول ایده آل بنزن-تولوئن برای کسر مولی بنزن در محلول و بنزن در بخار نشان داده شده است. مقادیر این نمودارها تنها برای بخش رنگی صحیح هستند. به طور مثال، در تصویر اول، تنها نقاط بالای نمودار که به رنگ سبز دیده میشوند دارای مفهوم هستند چراکه نقاط زیر خط نمودار، به حالت تعادلی مایع و بخار اشاره نمیکنند.
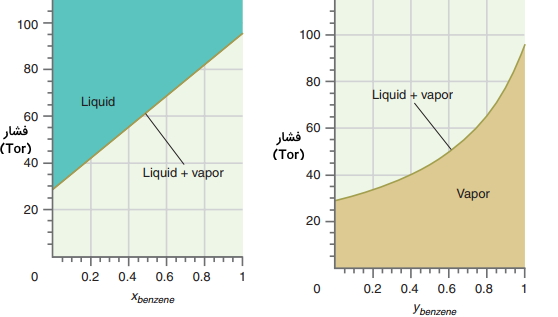
توجه داشته باشید که فشار به صورت تابعی از مقادیر متفاوت رسم شده است. برای مقایسه فاز گاز با ترکیب مایع در فشار مشخص، هر دو نمودار به صورت تابعی از Z بنزن رسم شدهاند که موسوم به ترکیب متوسط بنزن در کل سیستم است و نمودار آنرا میتوانید در تصویر زیر ببینید. Z در این سیستم به صورت مجموع مولهای مایع و بخار بنزن تقسیم بر تعداد کل مولها تعریف میشود که رابطه آن به صورت زیر است:
$$Z _ {\text {benzene}} = \frac {n _{\text {benzene}}^ {\text {liquid}} + n_ {\text {benzene} }^ {\text {vapor}} }{n _{\text {toluene}} ^ {\text {liguid} } + n_ {\text {toluene}} ^ {\text {vapor}}+ n _{\text {benzene}} ^ {\text {liquid}} + n _ {\text {benzene}} ^ {\text {vapor}}} = \frac { n _{\text {benzene}}}{n _ {\text {total} } }$$
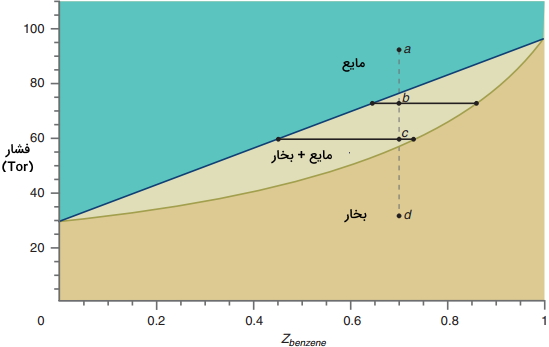
در منطقه آبی رنگ موسوم به مایع، سیستم در فاز مایع قرار دارد که در این حالت داریم:
$$Z _ {\text {benzene}} = x _ {\text {benzene}}$$
منطقهای که تنها بخار وجود دارد، با نام «بخار» مشخص شده است. در این حالت خواهیم داشت:
$$Z _ {\text {benzene}} = y _ {\text {benzene}}$$
محدودهای که بخش تکفاز مایع را از بخار جدا میکند، متناظر با محدوده دو فازی مایع-بخار است. در ادامه، قانون فاز را برای محلول ایده آل بنزن-تولوئن استفاده میکنیم که در آن، دو جزء و سه متغیر حالت مستقل T، P و Z داریم. از آنجایی که $$Z _ {\text {benzene}} =1 - Z _ {\text {toluene}}$$، بنابراین نمیتوان این دو متغیر را مستقل دانست. برای سیستمی با تعداد C جزء، قانون فاز به صورت زیر تعریف میشود که در آن F، C و p به ترتیب برابر با تعداد اجزا، درجه آزادی و تعداد فاز است.
$$F = C - p + 2$$
برای محلول ایده آل بنزن-تولوئن، تعداد اجزا برابر با ۲ است که از این طریق به رابط زیر میرسیم:
$$F = 4 - p$$
بنابراین، در محدوده تکفاز بخار و مایع تصویر بالا، درجه آزادی برابر با ۳ خواهد بود. یکی از این درجات آزادی، ثابت است چراکه در این تصویر، دما ثابت نگاه داشته شده است. در نتیجه، دو درجه آزادی باقیمانده برابر با P و $$Z _ {\text {benzene}}$$ خواهد بود. در ناحیه دوفازی که مایع و بخار داریم، تنها یک درجه آزادی در سیستم خواهیم داشت. اگر P ثابت باشد، مقادیر Z در انتهای خط افقی، $$x _ {\text {benzene}}$$ و $$y _ {\text {benzene}}$$ و در نتیجه $$Z _ {\text {benzene}}$$ را ثابت میکنند. توجه داشته باشید که تعداد اجزا میتوانند کمتر از تعداد ذرات شیمیایی باشند. به طور مثال، محلولی که ۳ ذره A، B و C را داشته و معادله شیمیایی $$A+ B \rightleftharpoons C$$ در آن برقرار باشد تنها شامل دو جزء مستقل خواهد بود زیرا تنها دو جزء از این ۳ جزء دارای غلظتهای مستقل هستند.
برای اینکه کاربرد این دیاگرام P-Z را بهتر درک کنیم، فرآیندی همدما را در نظر بگیرید که در آن، فشار سیستم از نقطه a شروع به کاهش میکند.از آنجایی که فشار در این حالت، بیشتر از $$P _ {total}$$ است، در حالت اولیه، سیستم به طور کامل در فاز مایع قرار دارد. تا زمانی که به خط جدا کننده فاز مایع و دوفازی برسیم، سیستم در حالت تکفاز باقی خواهند ماند. زمانی که به خط جدا کننده برسیم، سیستم وارد محدوده دوفازی خواهد شد. زمانی که به نقطه b برسیم، مقادیر $$x _ {\text {benzene}} $$ و $$y _ {\text {benzene}} $$ یعنی کسر مولی بنزن در فازهای مایع و بخار چه خواهد بود؟ برای پاسخ به این سوال باید، «خط اتصال» (Tie Line) را در محدوده دوفازی رسم کنیم.
این خط اتصال، خطی افقی در فشار مورد نظر است که نمودارهای $$P - x _ {\text {benzene}}$$ و $$P - y _ {\text {benzene}}$$ v را به یکدیگر متصل میکند. توجه داشته باشید که برای تمامی مقادیر فشار، مقدار $$y _ {\text {benzene}} $$، بیشتر از $$x _ {\text {benzene}} $$ است که این امر نشان میدهد فاز بخار در مقایسه با فاز مایع، همواره از اجزای فرار یا اجزایی با فشار بخار بیشتر تشکیل میشود.
مثال برای محاسبه ترکیب بخار در محلول ایده آل
یک محلول ایده آل حاوی 5 مول بنزن و 3/25 مول تولوئن در داخل یک سیستم سیلندر و پیستون قرار گرفته است. در دمای 298 کلوین فشار بخار بنزن و تولوئن به ترتیب برابر با 96/4 و 28/9 $$Torr$$ است.
- فشار بالای محلول از $$760 Torr$$ شروع به کاهش میکند. در چه فشاری، فاز بخار ظاهر میشود؟
- ترکیب بخار تحت این شرایط به چه صورت خواهد بود؟
کسر مولی اجزا در محلول برای بنزن و تولوئن به ترتیب برابر با 0/606 و 0/394 است. فشار بخار بالای محلول را به صورت زیر محاسبه میکنیم:
$$\begin {equation} \begin {aligned}
P_ {\text {total}} & = x _ {\text {benzene}} P _ {\text {benzene}} ^ {*} + x_ {\text {toluene}} P _ {\text {toluene}}^{*} \\
&=0.606 \times 96.4 \text { Torr } + 0.394 \times 28.9 \text { Torr } \\
&=69.8 \text { Torr }
\end {aligned} \end {equation}$$
فشار بدست آمده نشان میدهد زمانی فاز بخار خواهیم داشت که فشار تا این اندازه پایین آمده باشد. ترکیب بخار را در این فشار به صورت زیر محاسبه میکنیم:
$$\begin {equation} \begin {aligned}
y _ {\text {benzene} } & = \frac { P _ {\text {benzene} } ^ {*} P _ {\text {total} } - P_ {\text {benzene }} ^ {*} P _ {\text {toluene}} ^ {*}} { P _ {\text {total}} \left (P _{\text {benzene} } ^ {*} - P _ {\text {toluene}} ^ {*} \right)} \\
& = \frac {96.4 \text { Torr } \times 69.8 \text { Torr }-96.4 \text { Torr } \times 28.9 \text { Torr }}{69.8 \text { Torr } \times(96.4 \text { Torr }-28.9 \text { Torr })}=0.837 \\
y_{\text {toluene}}= & 1-y_ { \text {benzene}} =0.163
\end {aligned} \end {equation}$$
توجه داشته باشید که ترکیب بخار، بیشتر از مادهای تشکیل شده است که فشار بخار بیشتر و نقطه جوش پایینتری دارد.
محاسبه مقدار نسبی مواد در هر دو فاز
برای محاسبه مقدار نسبی هر دو فاز در منطقه دو فازی، رابطهای را برای محلول دو جزئی تعریف میکنیم. در تصویر زیر، نمای بزرگتری از تصویر قبل آورده شده است. در این تصویر، خط اتصال از نقطه b عبور میکند. برای بدست آوردن رابطه مورد نظر، طول خطوط lb و bv را محاسبه میکنیم.
$$\begin {equation} \begin {array} {l}
l b = Z _ { B } -x _ { B} = \frac { n _ {B}^ {t o t} } { n^{t o t}} - \frac {n_ {B}^ {l i q}} {n_{l i q} ^ {t o t}} \\
b v=y _ {B}- Z _{B}= \frac {n_ {B}^ {v a p o r} } {n_{v a p o r}^ { t o t}} - \frac { n_{B} ^ {t o t} } {n^{t o t}}
\end {array} \end {equation}$$
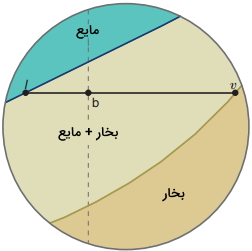
همانطور که در رابطه بالا نشان داده شد است برای اینکه تعداد مول کل یا تعداد مول در فازهای بخار و مایع را نشان دهیم، از بالانویس کمک میگیریم. با ضرب رابطه lb در $$n _ {liq} ^ {tot}$$ و ضرب رابطه bv در $$n _ {vapor} ^ {tot}$$ و تفریق دو رابطه از یکدیگر، به رابطه زیر خواهیم رسید:
$$\begin {equation}l b\ n_ {l i q} ^ {t o t}- b v\ n_ {v a p o r} ^ {t o t} = \frac {n _{B}^{t o t}} { n ^{ t o t} } \left (n _ {l i q} ^ {t o t} + n _ {v a p o r} ^ {t o t} \right ) - \left (n_ {B}^ {l i q} + n_ {B}^ {v a p o r} \right) = n _ {B} ^ {t o t} -n _{B} ^ {t o t}= 0 \end {equation}$$
$$\begin {equation} \frac {n _ {l i q} ^ {t o t}} {n _ {v a p} ^ {t o t } } = \frac { b \nu} { l b} \end {equation}$$
نتیجه بالا را میتوان به شکل زیر نوشت:
$$\begin {equation} n _ {l i q} ^ {t o t} \left ( Z _ { B } - x _ {B} \right) = n _ { \text {rapor } } ^ {\text {tot } } \left (y _ { B } - Z _ { B } \right ) \end {equation}$$
رابطه بالا به «قانون اهرم» (Lever Rule) معروف است به این دلیل که به اهرم و تکیهگاهی در نقطه b شباهت دارد. در نمودار بالا، نسبت bv به lb برابر با 2/34 است. در نتیجه، 70/1 درصد تعداد کل مولها در فاز مایع و 29/9 درصد در فاز بخار قرار دارند.
مثال برای محاسبه ترکیب اجزا در محلول ایده آل
برای محلول بنزن-تولوئن در مثال قبل، زمانی که 1/5 مول از محلول به بخار تبدیل شود، موارد زیر را حساب کنید:
- فشار کل
- ترکیب مایع
- ترکیب بخار
قانون اهرم را برای این مثال مینویسیم:
$$\begin {equation}n _ {\text {vapor}} ^ {\text {tot}} \left ( y _{ \text { benzene} } - Z _ {\text {benzene}} \right ) = n _ {\text {liq}} ^ {\text {tot}} \left ( Z _ {\text {benzene} } - x _ {\text {benzene} } \right ) \end {equation}$$
با وارد کردن دادههای سوال، به رابطه زیر میرسیم:
$$\begin {equation} 6.75 x _ {\text {benzene} } + 1.50 y _ {\text { benzene} } = 5.00 \end {equation}$$
فشار کل از رابطه زیر بدست میآید:
$$\begin {equation} \begin {aligned}
P _ {\text {total}} &=x _ {\text {benzene}} P_ {\text {benzene}} ^ {*} + \left ( 1 - x _ {\text {benzene} } \right) P_ {\text {toluene} } ^ {*} \\
& = \left [96.4 x _ { \text {benzene} } + 28.9 \left ( 1 - x _ {\text {benzene} } \right ) \right ] \text {Torr }
\end {aligned} \end {equation}$$
ترکیب بخار نیز از رابطه زیر بدست میآید:
$$\begin {equation} y _ {\text {benzene} } = \frac { P _ {\text {benzene} } ^ { * } P _ { \text {total} } - P _ {\text {benzene} } ^ {*} P _ {\text {toluene } } ^ { * } } {P _ {\text { t otal} } \left (P _ {\text {benzene }} ^ { * } - P _ { \text {toluene}}^ {*}\right)} = \left [\frac {96.4 \frac { P _ { \text {total} }} {\text {Torr} } - 2786} {67.5 \frac { P _ {\text {total} } }{\text {Torr }}}\right ] \end {equation}$$
در نهایت، یک دستگاه سه معادله سه مجهول داریم که با روشهای مختلفی قابل حل خواهد بود. در نهایت، جوابها اعداد زیر را شامل میشوند:
$$x _ {\text {benzene} } = 0.561$$
$$y _ {\text {benzene} } = 0.810$$
$$P _ {total} = 66.8 \ Torr$$
اگر این مطلب برای شما مفید بوده است، آموزشها و مطالب زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس شیمی
- مجموعه آموزشهای مهندسی شیمی
- آموزش مبانی شیمی فیزیک پلیمرها
- تابع حالت ترمودینامیکی — از صفر تا صد
- انرژی آزاد هلمهولتز — به زبان ساده
- جدول تناوبی — از صفر تا صد
^^