لیمیت در ریاضی چیست؟ — آموزش محاسبه و حل لیمیت — به زبان ساده با مثال

توابع و محاسبه آنها در نقاط مربوط به تابع، باعث میشود رفتار و تغییرات آنها شناخته شود. ولی در بعضی از حالتها یا نقطهها، توابع رفتار نامتعارفی دارند. در چنین نقاطی، رفتار حدی مورد توجه قرار میگیرد. این امر به این معنی است که میخواهیم با نزدیک شدن مقدار متغیر به یک نقطه، رفتار تابع را مورد مطالعه قرار دهیم. این کار در ریاضی به معنی حد یا لیمیت شناخته میشود.
برای آشنایی بیشتر با مفاهیم به کار رفته در این نوشتار، پیشنهاد میشود، متنهای مجموعه ها در ریاضیات – مفاهیم پایه و ضرب دکارتی مجموعه ها و مختصات دکارتی — به زبان ساده را مطالعه کنید. از آنجایی که در این نوشتار از سورها و گزارهها نیز استفاده شده، خواندن گزاره ها و سورهای منطقی — به زبان ساده و ترکیب گزاره های منطقی — به زبان ساده نیز خالی از لطف نخواهد بود.
لیمیت چیست ؟
در ریاضیات، حد یا لیمیت مقداری است که یک تابع (یا دنباله) با نزدیک شدن ورودی (یا متغیر) به مقداری از مقدارهای تابع، به آن نزدیک میشود. محاسبه لیمیت برای حساب و تحلیل ریاضی ضروری است و برای تعریف پیوستگی، مشتقات و انتگرال توابع ریاضی مورد استفاده قرار میگیرد. جدا از لیمیت توابع ریاضی، مفهوم لیمیت یک دنباله بیشتر به مفهوم لیمیت یک شبکه توپولوژیک تعمیم داده میشود و با حد و حد مستقیم در نظریه رده ارتباط نزدیک دارد.
در فرمولها، حد یا لیمیت یک تابع مثل معمولاً به صورت زیر نوشته میشود.
رابطه بالا به صورت زیر خوانده میشود.
لیمیت تابع f زمانی که متغیر x به c میرود برابر است با L
از طرفی میتوان لیمیت تابع f را به صورت زیر نمایش داد.
به این ترتیب عبارت بالا به صورت زیر خوانده خواهد شد.
تابع f به L میل میکند، زمانی که x به سمت c میل کند.
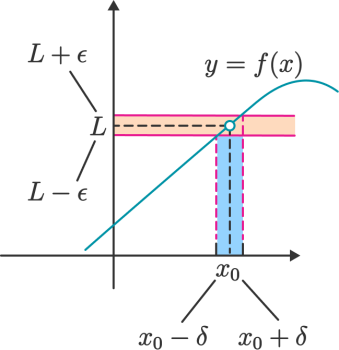
لیمیت در ریاضی
فرض کنید تابع یک تابع حقیقی و نیز یک مقدار حقیقی باشد. لیمیت تابع f که آن را با نشان میدهیم، بیان کننده آن است که با نزدیکی مقدار به و کاهش اختلاف آنها به میزان کافی، تابع هم به نزدیک خواهد شد. در صورتی که این اتفاق بیافتد، میگویم حد تابع در نقطه ، برابر با L است.
«آگوستین کوشی» (Augustin-Louis Cauchy) در سال ۱۸۲۱ به همراه «کارل وایشتراس» (Karl Weierstrass)، تعریف حد را فرموله کرده و براساس تعریف حد توسط اپسیلون () و دلتا () مشخص کردند.
بیان حد به وسیله () و () به صورت زیر است.
اگر در یک همسایگی با مرکز و با شعاع تغییر کند، آنگاه تابع نیز در یک همسایگی با مرکز و شعاع قرار میگیرد. این موضوع را به بیان ریاضی به صورت زیر خواهیم نوشت.
واضح است که قدر مطلقهای به کار رفته در رابطه بالا، باعث ایجاد همسایگی خواهند شد.
مثال ۱:
به منظور استفاده از این رابطه برای محاسبه حد تابع زیر را در نظر بگیرید. میخواهیم لیمیت این تابع را زمانی که به سمت ۱ میل میکند محاسبه کنیم.
با توجه به این موضوع حد را به صورت زیر خواهیم نوشت.
از قاعده یا بیان حد به وسیله () و () استفاده میکنیم.
واضح است که مقدار ۱ در دامنه این تابع قرار دارد، پس میتوانیم برای بدست آوردن این حد، مقدار تابع را در این نقطه بدست آورید و آن را به عنوان حدسی اولیه برای حد به کار بریم. مقدار تابع در این حالت برابر است با . در نتیجه مقدار را همان در نظر میگیریم.
به این ترتیب رابطه لیمیت یا حد برای این مثال، به صورت زیر نوشته میشود.
از سمت راست تعریف استفاده میکنیم و برای هر ، وجود را نشان میدهیم.
پس با قرار دادن در یک همسایگی به نتیجه میرسیم که با قرار دادن بزرگتر از به پاسخ خواهیم رسید. پس برای هر توانستیم مقدار را تعیین کنیم (که مقداری بزرگتر از است) تا رابطه مربوط به حد یا لیمیت در آن تعریف شود. بنابراین مقدار حد تابع مورد نظر است.
قضیهای در حد وجود که دارد که به یکتا بودن حد کمک میکند. در این حالت اگر تابعی دارای حد باشد، آن حد منحصر بفرد خواهد بود و هیج نقطهای دیگر نمیتواند حد تابع باشد. بنابراین مقدار ۲ برای حد تابع بالا، مقداری منحصر بفرد خواهد بود و تابع در نقطه حد دیگری نخواهد داشت.
همانطور که مشاهده میکنید، زمانی که با یک تابع خطی یا به طور کل چند جملهای مثل مواجه هستیم، دامنه تابع برابر با اعداد حقیقی است و حد چنین تابعی، مقدار آن در همان نقطه است. پس میتوان رابطه زیر را برای چند جملهایها نوشت.
در حالت کلی اگر و دو تابع چند جملهای با درجه و باشند، آنگاه جمع، تفریق، ضرب آنها دارای حد است و حد یا لیمیت آن برابر است با مقدار حاصل چندجملهای ها در مثلا نقطه . ولی در تقسیم این خاصیت برقرار نیست و چون در ریشه مخرج، کسر به صورت نامعین در میآید، باید بوسیله روشهایی، نسبت دو چند جملهای را به شکلی درآوریم که رفع ابعام شود. در مثال زیر چنین حالتی رخ داده و سعی میکنیم، رفتار حدی تابع را در نزدیکی ریشه مخرج مشخص کنیم.
مثال ۲:
تابع زیر را در نظر بگیرید. میخواهیم حد آن را زمانی که متغیر به سمت ۱ میل میکند، بدست آوریم. این کار به این معنی است که رفتار تابع در حول مقدار ۱ را مشخص کنیم. واضح است که این بار، مقدار ۱ در دامنه تابع قرار نداشته و نمیتوان مقدار تابع را در آن محاسبه کرد.
ابتدا مقدار این تابع را طبق جدول محاسباتی زیر در نزدیکی ۱ بدست میآوریم.
| مقدار متغیر | مقدار تابع |
| ۰٫۹ | f(۰٫۹) = ۱٫۹۰۰ |
| ۰٫۹۹ | f(۰٫۹۹) = ۱٫۹۹۰ |
| ۰٫۹۹۹ | f(۰٫۹۹۹) = ۱٫۹۹۹ |
| ۱٫۰ | نامعین (تعریف نشده) |
| ۱٫۰۰۱ | f(۱٫00۱) = ۲٫001 |
| ۱٫۰۱ | f(۱٫01) = ۲٫010 |
| ۱٫۱ | f(۱٫۱) = ۲٫۱ |
این طور به نظر میرسد که مقدار این تابع در حول ۱، به سمت ۲ میل میکند. میخواهیم این موضوع را به کمک تعریف اولیه حد به کار گیریم. مشخص است که حدس اولیه یا مقدار را برابر با ۲ در نظر خواهیم گرفت.
به کمک اتحادها، صورت کسر را به تجزیه کرده و آن را به صورت زیر خواهیم نوشت.
به این ترتیب تابع را به صورت سادهتری نوشته و براساس ، حد را پیدا میکنیم. ولی توجه داشته باشید که در این حالت، دامنه تابع شامل مقدار ۱ نخواهد بود.
همانطور که در مثال قبل یک مسئله لیمیت را حل کردیم، اینجا هم به کمک رابطه گفته شده در تعریف لیمیت مثال را حل کرده و مقدار حد را برابر با ۲ بدست خواهیم آورد.
مثال ۳:
فرض کنید تابعی به صورت زیر به ما داده شده و قرار است، حد این تابع را در نقطه تعیین کنیم.
مشخص است که تابع مورد نظر، یک تابع پلهای یا چند ضابطهای است. باز هم به کمک قاعده یا روش اسپیلن-دلتا، میخواهیم، حد این تابع را محاسبه کنیم. فرض کنید که حد تابع را 2 در نظر گفته باشیم (زیرا مقدار تابع در نقطه برابر با ۲ است). پس مقدار بوده و رابطه حد را خواهیم نوشت.
باید به ازاء هر مقداری از ، بتوانیم مقداری برای پیدا کنیم. رابطه بالا را به ازاء مقدار نامنفی (یعنی ) بازنویسی میکنیم.
از آنجای برای همه مقادیر مثبت رابطه گفته شده، باید صادق باشد، میتوانیم حد تابع را برابر با 2 در نظر بگیریم.
این بار از مقادیر منفی کمک میگیریم. اگر باشد، رابطه حد به صورت زیر نوشته خواهد شد.
مشخص است که رابطه اخیر، فقط برای مقدارهایی از برقرار است که از ۱ بزرگتر هستند، پس نمیتوانیم حد تابع را برای مقادیر منفی متغیر ، مقدار ۲ در نظر بگیریم. در نتیجه تابع در نقطه دارای حد نیست.
البته توجه دارید که به کمک قضیههای مربوط به حد، مقدار حد باید منحصر به فرد باشد. به بیان دیگر نمیتوان حد تابع در یک نقطه، دارای دو جواب باشد. میتوان نشان داد که حد تابع برای زمانی که متغیر به سمت صفر میل میکند، در حالتی که از نقاطی بزرگتر از صفر (سمت راست) به صفر نزدیک میشویم، برابر با ۲ و برای مقادیری که از صفر کوچکتر هستند (از سمت چپ) برابر با ۱ است. در نتیجه تابع حد نخواهد داشت.
نکته: مقداری از که از سمت چپ به نقطه صفر نزدیک میشوند، حد چپ تابع را میسازند. از طرفی نزدیک شدن از سمت راست به تابع نیز حد راست آن را تعیین میکند. طبق قضیه حد، باید حد راست و حد چپ با یکدیگر برابر بوده تا تابع در آن نقطه دارای حد باشد.
مثال ۴:
براساس مثال ۳ میتوان نشان داد که حد تابع زیر در هر نقطهای از مقادیر حقیقی (دامنه تابع) وجود ندارد.
منظور از irrational، اعداد گنگ و rational نیز اعداد گویا است.
فرض کنید بخواهیم حد تابع را در نقطهای مثل بررسی کنیم. در هر همسایگی از هم اعداد گنگ وجود دارد و هم اعداد اصم در نتیجه نمیتوان حد تابع را در هر همسایگی به شعاع مشخص کرد. در نتیجه تابع بالا در هیچ نقطهای (چه گویا چه اصم) که در دامنهاش است، حد ندارد.
کاربرد لیمیت
هنگامی که رفتار توابع در ریاضی را بررسی میکنیم، پیوستگی توابع مطرح میشود. تابعی که نقطههای آن به یکدیگر متصل بوده و هنگام رسم نمودار آن، قلم از روی کاغذ برداشته نشود، یک تابع پیوسته است.
برای مثال اگر قرار باشد، تابعی مثل در نقطه ، پیوسته باشد باید نقطه در دامنه تابع قرار داشته باشد و بتوان تابع را در آن نقطه محاسبه کرد. از طرفی حد یا لیمیت تابع نیز در این نقطه با مقدار تابع در آن نقطه برابر باشد. با برقرار بودن این شرایط، تابع را در پیوسته میگوییم. اگر تابعی در همه نقاط دامنهاش، پیوسته باشد، تابع کلا پیوسته خواهد بود.
همچنین تعریفی که برای مشتق به کار میرود، برگرفته از مفهوم حد است. تابع در نقطه دارای مشتق است، اگر حد یا لیمیت زیر وجود داشته و بینهایت نباشد.
همانطور که در رابطه بالا میبینید، مشتق تابع را به صورت نشان میدهیم. چنانچه تابعی در همه دامنهاش، دارای مشتق باشد، آن را مشتقپذیر میگویند.
از طرفی انتگرال نیز برحسب حد بیان میشود. به تصویر زیر توجه کنید. هدف آن است که سطح زیر منحنی را تعیین کنیم.
فرض کنید تابع مورد نظر را که در بازه پیوسته است، به زیربازه مساوی به عرض تقسیم کردهایم. از طرفی برای هر زیربازه، نقطهای مثل را در نظر گرفتهایم تا نشانگر مقدار تقریبی تابع در آن بازه باشد. آنگاه انتگرال معین تابع از تا برابر را رابطه زیر خواهد بود.
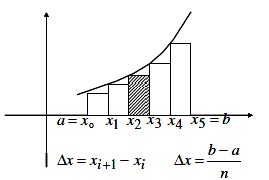
نکته: توجه داشته باشید که در اینجا ، بس با تقریب نقصانی میتوان بوده یا با تقریب اضافی را برای تابع صعودی در نظر گرفت. در صورتی که f(x)g(x)x=cLMh(x) = f(x) \pm g(x)cL \pm Mp(x) = f(x) \cdot g(x)cL \cdot M\dfrac{f(x)}{g(x)}c\dfrac{L}{M}c$$ ریشه مخرج باشد.
خلاصه و جمعبندی
همانطور که در این متن خواندید، مبنای تعریف مشتق و به دنبال آن انتگرال، تسلط به محاسبه حد و محاسبات مربوطه است. به همین دلیل حد یا لیمیت در ریاضی از اهمیت زیادی برخوردار است. در اینجا به مفهوم و نحوه محاسبه لیمیت براساس تعریف اولیه پرداختیم ولی در نوشتارهای دیگر مجله فرادرس از جمله تقلب نامه (Cheat Sheet) مفاهیم و روابط حد و پیوستگی میتوانید به شیوه محاسبه حد به روشهای مختلف دسترسی پیدا کنید.












