بی نهایت و مفهوم آن — به زبان ساده

شاید اغلب مردم فکر کنند «بینهایت» (Infinity) به معنی بسیار بزرگ یا بسیار زیاد است. در حالیکه از لحاظ علمی، بی نهایت به معنی بیپایان یا شمارش ناپذیر است. از آنجایی که در ریاضیات از مفهوم بینهایت استفادههای زیادی میشود، در این نوشتار سعی میکنیم با بی نهایت و مفهوم آن بیشتر آشنا شده و اشتباهاتی که ممکن است در درک آن وجود داشته باشد را برطرف کنیم.
بی نهایت، پایان ندارد
ایده بینهایت برای چیزهایی که دارای پایانی نیستند به کار میرود. متاسفانه (یا خوشبختانه) در دنیای واقعی و معمولی ما چیزی نیست که پایانی نداشته باشد، به همین دلیل با حواس پنچگانه نمیتوان بی نهایت را درک کرد. پس تنها راه باقی مانده برای درک بینهایت، تصور کردن آن است.
اگر با تفکر در مورد بینهایت، مفاهیم «بیپایان» (Endless) یا «بیکران بودن» (Boundless) در ذهن شما قرار میگیرد، بینهایت را درست درک کردهاید. در مقابل هر چیزی که «با پایان» (Finite) یا «کراندار» (Bounded) است، بینهایت نیست.
شاید در بحث پدیدههای بیپایان تصور شود که بینهایت به معنی افزایش مداوم باشد. ولی باز هم این تصور صحیح نیست. بینهایت چیزی نیست که بیپایان بودنش به علت رشد یا افزایش باشد. پس باید پذیرفت که بینهایت به عنوان یک مفهوم به معنی چیزی است که با تصور هر چیز خیلی خیلی .... بزرگ باز هم از آن بزرگتر است. در نتیجه نمیتوان بینهایت را اندازهگیری کرد. حتی اندازه کهکشانها نیز بینهایت نیست.
بی نهایت، مفهومی ساده
هر چند به نظر میرسد بینهایت بسیار پیچیده است، ولی هر روز با مفاهیمی سروکار داریم که بینهایت در تعریف آنها نقش دارد. برای مثال در هندسه، تعریف انواع خط به صورت زیر تعریف میشوند:
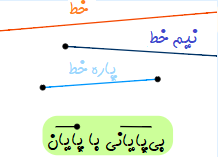
- خط، از دو طرف ادامه دارد و برای آن نقطه شروع یا پایانی وجود ندارد.
- نیم خط، خطی است که از یک طرف دارای پایان است.
- پاره خط، دارای ابتدا و انتها پس پایاندار است.
برای روشن شدن موضوع به مثالهای دیگری در این زمینه توجه کنید.
- مجموعه اعداد طبیعی، یک مجموعه بیپایان است و تعداد اعضای این مجموعه بی نهایت است.
- کسر که یک عدد متناهی است که به صورت نوشته میشود. علامت بالای رقم 3 که به صورت یک پارهخط ظاهر شده، بیان میکند که تعداد رقم ۳ در آن بینهایت است و هیچگاه پایان نمییابد.
- یک دنباله نامتناهی از حرف A که در انتهای آن حرف B ظاهر شود، هرگز وجود ندارد، زیرا هیچگاه حرف A در این دنباله پایان نمییابند تا حرف B ظاهر شود.
- بینهایت نقطه روی یک خط قرار دارد حتی اگر پاره خط باشد. زیرا خط از بینهایت نقطه تشکیل شده است. تقسیم خط به اجزای کوچکتر هرگز از بینهایت نقطه آن نمیکاهد.
متناهی و اعداد بزرگ
اعداد بسیار بزرگی برای انسان شناخته شده است که حتی از تعداد ذرات بنیادی جهان بزرگتر هستند. برای مثال «گوگول» (Googol) نام عددی است که به صورت ۱ با ۱۰۰ صفر در جلویش نمایش داده میشود. به بیان دیگر میتوان آن را به صورت نشان داد. به راحتی میتوان این عدد بسیار بزرگ را بسیار بسیار بزرگتر کرد. برای مثال می توان یک گوگول را به توان ۱۰۰ رساند و نوشت . با توجه به اینکه بالاخره تعداد ارقام این اعداد متناهی است، هیچکدام بینهایت نیستند.
استفاده از بی نهایت
گاهی در محاسبات از بینهایت به مانند اعداد استفاده میکنیم و گاهی نیز نتیجه را ناشناخته و بیمعنی میشناسیم. معمولا در ریاضیات برای نمایش بی نهایت از نماد استفاده میشود.
اگر بنویسیم به این معنی است که x یک عدد حقیقی است. این نامساوی را به صورت «x از منفی بینهایت تا بینهایت» میخوانیم. همچنین اگر بنویسیم مشخص است اضافه کردن ۱ به بی نهایت به آن چیزی اضافه نمیکند. بنابراین خواهیم داشت . جدول زیر به درک روابط و محاسبات مربوط به به ما کمک میکند.
| x>0 |
| x<0 |
عملیات زیر برای بی نهایت تعریف نشده است.
نکته: توجه داشته باشید که بینهایت، یک معنی حدی برای توابع نیز دارد. به این معنی که برای نمایش دادن رفتار یک نسبت یا عدد برای مقادیر بسیار بسیار بزرگ به کار میرود. در این حالت میگویم، مثلا تابع در نقطه ۱ دارای حد بینهایت است. در حالیکه مفهوم تعریف نشده، یک رابطه حدی را نشان نمیدهد. به رابطههای زیر توجه کنید.
در مقابل تقسیم زیر را «نامعین» (با نماد «ن») مینامیم.
مجموعههای نامتناهی و بی نهایت
اگر به بررسی مجموعههای نامتناهی مشغول هستید، حتما به تعداد اعضای چنین مجموعههایی سروکار دارید. به این ترتیب میتوان برای اجتماع این گونه مجموعهها، تعداد اعضا را مشخص کرد. برای بیان اندازه مجموعه اعداد طبیعی از نام الف-صفر استفاده میشود که آن را به صورت نشان میدهند. به این ترتیب میتوان تعداد اعضای مجموعههای نامتناهی را با استفاده از تناظر با مجموعه اعداد طبیعی نشان داد.
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس رسمی دبیرستان و پیش دانشگاهی
- مجموعه آموزشهای ریاضیات
- اعداد اصلی، ترتیبی و اسمی – مفاهیم و تعاریف به زبان ساده
- اعداد مختلط – به زبان ساده
- مجموعه ها در ریاضیات – مفاهیم پایه
- عدد اویلر یا نپر – به زبان ساده
- تعریف های ابتدایی جبر – به زبان ساده
- آموزش ریشه یابی و ترسیم اعداد مختلط در متلب













سلام با اجازه عکس اول سایت رو استفاده میکنم
با سلام؛
برای استفاده از مطالب مجله فرادرس میتوانید به «شرایط استفاده» در انتهای صفحه یا این لینک مراجعه کنید.
با تشکر از همراهی شما با مجله فرادرس
اگر بی نهایت صفر را با هم جمع کنیم عدد 1 بدست می آید!
0+0+0+…+0 = ∞ * 0 = 1
یک بار دیگه به متن دقت کنید:
صفر در بینهایت تعریف نشده است
با سلام
اگه ممکنه بهواین سوالات پاسخ بدیدد:
۱) آیا بی نهایت در فیزیک و دنیای واقعی وجود دارد؟
۲) آیا امکان دارد بی نهایت گسسته ها داشته باشیم؟
مثلا بی نهایت آجر داشته باشیم؟
۳) آیا میشود از بی نهایت چیزی کم کننیم یا اضافه کنیم؟
با تشکر
سلام وقت بخیر.
بازه منفی بی نهایت تا منفی۲ بزرگتر است یا
مثبت ۳ تا مثبت بی نهایت؟
سلام و روز شما به خیر؛
پیشنهاد ما به شما این است که مطلب جهان موازی چیست ؟ | هر آنچه باید بدانید را مطالعه کنید.
از همراهی شما با فرادرس خرسندیم.
از نظر حقیر،ما مفهومی به نام بی نهایت مثبت و منفی یا بی نهایت به علاوه یک یا منهای یک نداریم،جهان کلا یکدست بی نهایت است و ما بین این بی نهایت ها هستیم،همه چیز در جهان از یک نقطه شروع می شود ،نقطه را هر کجا بگذاری دنیای اطرافش شکل می گیرد و خود نقطه یک مفهوم است و این بوده که صفر نقطه شروع اعداد دنیای ما شد،به نظر من واقعیت این است که جهان تا انجایی که می دانیم ممکن است بی نهایت باشد و یعنی نه اغازی و نه پایانی،یکدست از بی نهایت ها تا بی نهایت ها،اگرنقطه اغاز اعداد از بی نهایت بود دیگر عدد منفی نداشتیم همه چیز مثبت بود،اگر مغز ما محدود نبود و می توانستیم چنین کاری را بکنیم دیگر همه چیز واقعی بود،ولی فعلا دسترسی به این امکان پذیر نیست.در نتیجه هیچ چیز در دنیا قطعی نیس و نسبی است تا زمانی که ما بتوانیم به بی نهایت برسیم،و اگر رسیدیم شاید بتوانیم خالق جهان را بشناسیم.
نظر شما راجع به اتم های اگزاتیک پوزیترونیوم در شرایطی که تعداد لپتون ها و پاد لپتون ها با هم برابر باشد و نیروی اثر گذار هسته ای در خارج از محدوده الکترون ها داشته باشیم و بتوانیم اکسید کاذبی در ترکیب ایجاد کنیم که باعث جلو گیری از تشعشات رادیو اکتیو و سهولت در انجام ازمایش ها بشود چیست؟
سلام
چیزی که در مورد بینهایت برای من مسلّم و قطعی است، این است که بی نهایت نمیتواند دارای یک مرکز واحد و یگانه و منحصر به فرد باشد. زیرا مرکز دار بودن هر چیزی نشانه محدود بودن و محیط و مرز داشتن آن چیز می باشد. اما بینهایت میتواند دارای مراکز بیشمار محلی و منطقه ای باشد. هرکدام از این محله و یا منطقه ها را می توان یک جهان و مجموعه در حال افزایش آنها را جهان های موازی و بیشمار نامید. از آنجاییکه تقسیم بینهایت به واحد های محدود جهانی پایان ناپذیر می باشد، میتوان چنین تقسیمی را ” کثرت پایان ناپذیر ماورایی ” نامید. این ایده را میتوان به عنوان یک دلیل غیر قابل رد در جهت اثبات وجود جهان های موازی و بیشمار در نظر گرفت. دلیل دوم به شرح زیر می باشد: هستی بیکران هرگز قادر نخواهد بود که از یک حالت کلی به یک کلی دیگر تغییر و تحول یابد، زیرا برای این حرکت تحولی به بینهایت زمان ها نیاز خواهد داشت. لذا برای رفع این مشکل هستی بیکران با آگاهی و دانش و قدرت مطلق و بیکران، خودرا به هستی های محدود و متناهی و مساوی تقسیم نموده است، تا این هستی های محدود هرکدام بتوانند در طی یک زمان معین از یک حالت کلی به یک حالت کلی دیگر تحول یابند. و این تحولات از طریق وقوع مه بانگ های متوالی و بیشمار بر اثر نوسانات متواتر یا پی در پی کیهانی صورت می پذیرند. حرکت هستی های محدود و متناهی دو جهته میباشد؛ یکی نزولی و دیگری صعودی و منزل به منزل.
حال باید تعداد منازل را تعیین کرد. حدس و گمان و احتمال این حقیر عدد 7 میباشد.
که از لحاظ عددی با وادی ها و شهر های هفتگانه عشق عارفان بزرگ دینی تطابق دارد، اما محتوایی کاملا متفاوت.
بسیار سنگین