تابع چند ضابطه ای – به زبان ساده

«تابع چند ضابطه ای» یا تکه‌ای (Piecewise Function) تابعی است که چند تکه یا بخش دارد. این نوع توابع به صورت تکه تکه و با چند ضابطه مختلف برای هر تکه در بازه‌های مربوط به آن‌ها تعریف می‌شوند. در این آموزش، با تابع چند ضابطه ای آشنا می‌شویم.

تابع چند ضابطه ای

تابع چند ضابطه ای به چندین بخش یا تکه تقسیم می‌شود. هر تکه متفاوت با تکه‌های دیگر است و بر اساس ضابطه تعریف شده در آن بازه رفتار می‌کند.

این تکه‌ها می‌توانند نقطه، خط یا منحنی باشند. برای مثال، تابع چند ضابطه ای زیر سه تکه دارد. تکه روی بازه $$- 4 \leq x \leq - 1$$ تابع $$f ( x ) = 3 x + 5$$ را نمایش می‌دهد. تکه بازه $$- 1 \le x < 3$$ نشان دهنده تابع $$f ( x ) = 2$$ است و در نهایت، روی بازه $$3 \le x \le 4$$ تابع $$f ( x ) = - x + 2$$ را داریم.

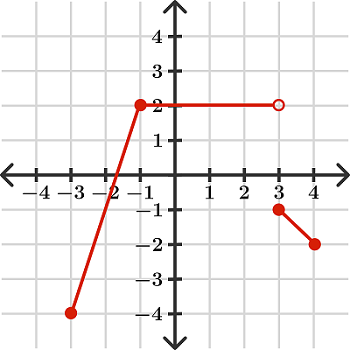
با استفاده از نمادگذاری تابع، نمودار را به صورت زیر نمایش می‌دهیم:

$$\large f ( x ) = \begin {cases} 3 x + 5 & - 4 \leq x \leq - 1 \\ 2 & - 1 \leq x < 3 \\ - x + 2 & 3 \leq x \leq 4 \end {cases} .$$

مثالی از تابع چند ضابطه ای

یک کارخانه تولید ورق، هزینه پایه‌ای معادل با ۲ دلار به علاوه هزینه وابسته به زمان ۰٫۵ دلار در دقیقه دارد. البته، قبل از طی یک زمان مشخص، هزینه ثابت و مقدار آن ۷ است. کدام تابع زیر، هزینه $$f ( x )$$ تولید ورق را برای $$x$$ دقیقه نشان می‌دهد؟

(الف)

$$\large f ( x ) = \begin {cases} 7 & 0 < x \leq 7 \\ 2 + 0.5 0 x & x > 7 \end {cases}$$

(ب)

$$\large f ( x ) = \begin {cases} 7 & 0 < x \leq 10 \\ 2 + 0.5 0 x & x > 10 \end {cases}$$

(ج)

$$\large f ( x ) = \begin {cases} 7 & 0 < x \leq 1 4 \\ 2 + 0.5 0 x & x > 14 \end {cases}$$

پاسخ: می‌دانیم که $$x$$ تعداد دقیقه‌ها است. همان‌طور که گفتیم، هزینه قبل از رسیدن به یک زمان مشخص، ثابت و برابر با ۷ دلار است. بنابراین، لازم است بدانیم در چه لحظه‌ای که هزینه ۷ دلار است. این زمانی است که تساوی $$2 + 0.5 x = 7$$ را داشته باشیم، بنابراین $$x = 5$$ یا $$x = 10$$ خواهد بود. در نتیجه، تابع (ب) جواب صحیح است.

مثالی از تابع قدر مطلق

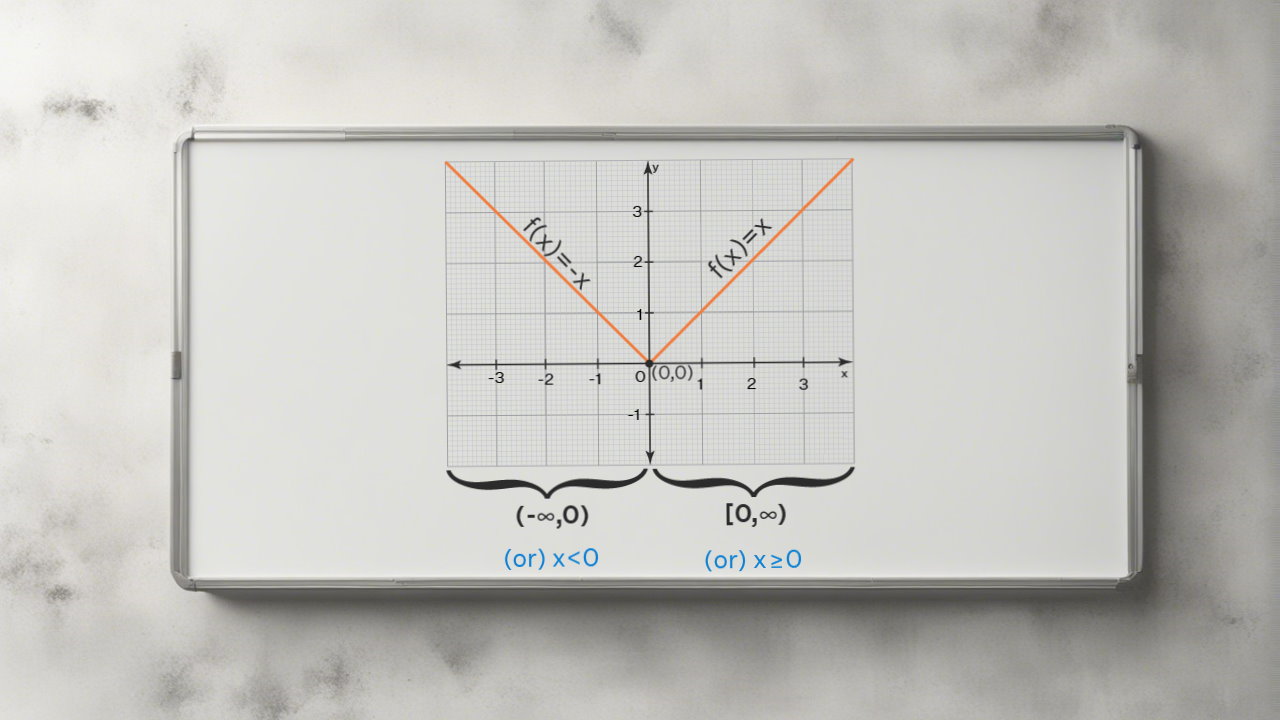
یکی از توابع چند ضابطه ای معروف تابع قدر مطلق است. چگونه می‌توانیم تابع $$f ( x ) = | x |$$ را به صورت یک تابع چند ضابطه ای بنویسیم؟

حل: تابع $$f ( x ) = |x |$$ ترکیبی از دو تابع خطی است و می‌توان آن را به صورت یک تابع دوضابطه‌ای نوشت:

$$\large f ( x ) = \begin {cases} - x & x < 0 \\ x & x \geq 0 \end {cases} .$$

ارزیابی توابع چند جمله ای

وقتی بخواهیم یک تابع چند ضابطه ای را ارزیابی کنیم (مقدار آن را به ازای نقاط داده شده به دست آوریم)، لازم است مقدار تابع را در هر تکه‌ای که لازم است، محاسبه کنیم. فرض کنید می‌‌خواهیم $$f ( - 2 )$$ را محاسبه کنیم. اگر $$f ( x )$$ به صورت زیر باشد:

$$\large f ( x ) = \begin {cases} 3 x + 5 & - 4 \leq x \leq - 1 \\ 2 & - 1 \leq x < 3 \\ - x + 2 & 3 \leq x \leq 4 \end {cases} .$$

فیلم آموزش ریاضی و آمار ۲ – پایه یازدهم علوم انسانی در فرادرس

کلیک کنید

$$f ( - 2)$$ مشخص می‌کند که می‌خواهیم مقدار تابع را در $$x = - 2$$ تعیین کنیم. مقدار $$- 2$$ در بازه اول قرار دارد که در آن، برای $$- 4 \le x \le - 1$$ مقدار $$f ( x ) = 3 x + 5$$ را داریم. بنابراین، $$f ( - 2 ) = 3 (- 2 ) + 5 = - 1$$.

مثالی از محاسبه تابع چند ضابطه ای

اگر $$f ( x )$$ به صورت زیر باشد، مقدار $$f ( 3)$$ را به دست آورید.

$$\large f ( x ) = \begin {cases} 3 x - 2 & - 5 \leq x < 2 \\ x ^ 2 + 1 & 2 \leq x < 4 \\ - 3 x + 1 & x \geq4 \end {cases} .$$

حل: $$f ( 3 )$$ در بازه $$2 \le x < 4$$ قرار دارد که در آن، $$f ( x ) = x ^ 2 + 1$$ است. بنابراین، $$f ( 3 ) = 3 ^ 2 + 1 = 10$$.

مثالی از پیوستگی تابع چند ضابطه ای

اگر تابع چند ضابطه ای $$f$$ به صورت زیر تعریف شده و پیوسته باشد، مقدار $$Q$$ را به دست آورید.

$$\large f ( x ) = \begin {cases} - 3 x + 2 & x \leq 2 \\ x^2 - Q & x > 2 \end {cases}$$

حل: در $$x = 2$$، نمودار $$y = - 3 x + 2$$ در نقطه $$( 2 , - 4 )$$ قرار دارد. وقتی $$Q = 0$$ و $$x= 2$$ باشد، نمودار $$y = x ^ 2 - Q$$ در نقطه $$( 2 , 4 )$$ قرار دارد. بنابراین، باید منحنی سهمی را به اندازه $$4 + 4 = 8$$ به پایین جابه‌جا کنیم تا نقاط منطبق شوند. در نتیجه، $$Q = 8$$ است.

رسم توابع چند ضابطه ای

برای رسم یک تابع چند ضابطه ای، تکه‌های مختلف را برای زیربازه‌ها رسم می‌کنیم. برای مثال، می‌خواهیم نمودار تابع زیر را رسم کنیم:

$$\large f ( x ) = \begin {cases} 2 x + 1 & x \leq - 1 \\ x ^ 2 & - 1 < x \leq 2 \\ 4 & x > 2 \end {cases} .$$

این منحنی چندتکه دارای سه بخش یا تکه و دو نقطه مرزی در $$x = - 1$$ و $$x = 2$$ است. تکه اول منحنی تابع خطی $$f ( x ) = 2 x + 1$$ برای $$x \le - 1$$ است. با توجه به اینکه $$f ( - 1 ) = 2 ( - 1 ) + 1 = - 1$$، نقطه‌ای توپر در $$( - 1 , - 1 )$$ داریم. در ادامه، یک تابع درجه دوم $$f ( x ) = x ^ 2$$ برای $$-1< x < 2$$ با نقاط مرزی $$- 1$$ و $$2$$ داریم. با توجه به $$f ( - 1 ) = ( - 1 ) ^ 2 = 1$$، یک نقطه توخالی در $$( - 1 , 1 )$$ و $$f ( 2 ) = 2 ^ 2 = 4$$ داریم، به گونه‌ای که یک نقطه توپر در $$( 2 , 4 )$$ خواهیم داشت.

تکه سوم تابع خطی افقی $$f ( x ) = 4$$ از $$x = 2$$ تا بینهایت است. شکل زیر، مراحل رسم نمودار این تابع چند ضابطه ای را از چپ به راست نشان می‌دهد.

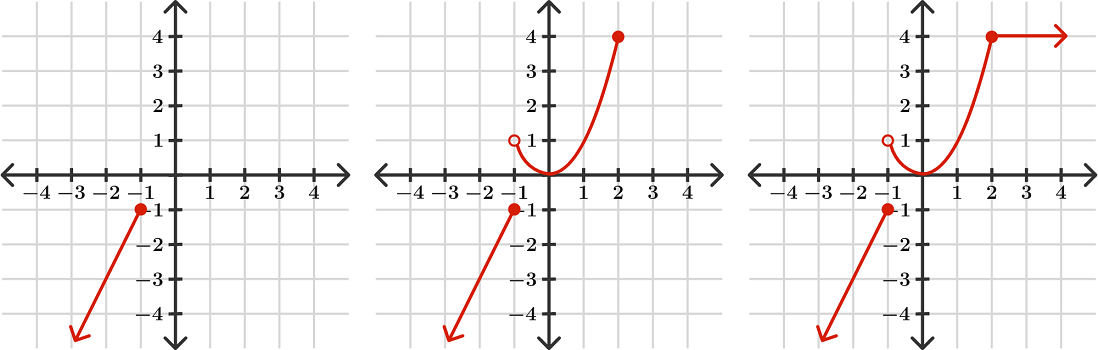
مثال رسم تابع چند ضابطه ای

نمودار صحیح تابع زیر، کدام‌یک از شکل‌های زیر است؟

$$\large f ( x ) = \begin {cases} - 2 x + 1 & x \leq 2 \\ \frac { 1 } { 2 } x - 4 & x > 2 \end {cases}$$

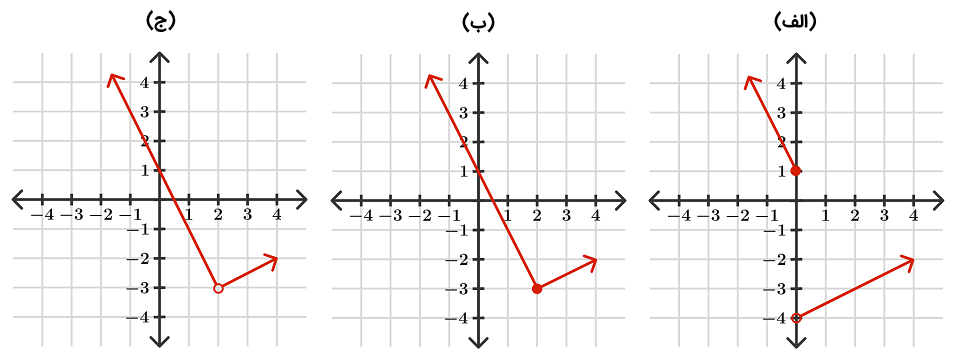
حل: در نمودار (الف) توابع به درستی رسم شده‌اند، اما نقطه مرزی به جای $$x = 2$$ به اشتباه در $$x = 0$$ قرار دارد. نمودار (ج) نیز نمودارهای صحیح دارد و نقطه مرزی صحیح است، اما نقطه باید یک نقطه توپر باشد، زیرا تابع اول شامل مقدار $$x = 2$$ است. بنابراین، نمودار (ب) صحیح است.