قضیه شوارتز و تقارن در مشتق دوم | به زبان ساده

یکی از شاهکارهای ریاضی که توسط «لایبنیتس» (Gottfried Wilhelm Leibniz) و «اسحاق نیوتن» (Isaac Newton) ابداع شد، «مشتق» (Derivation) و موضوع مشتق‌پذیری است که برای توابع یک و چند متغیره قابل محاسبه است. مباحث مربوط به مشتق و انتگرال، پایه‌های حسابان و ریاضیات پیشرفته محسوب می‌شوند. در این نوشتار به بررسی مشتق دوم و شرط تقارن آن در توابع چند متغیره می‌پردازیم. در این بین قضیه شوارتز و تقارن در مشتق دوم اهمیت زیادی در شناخت خواص توابع چند متغیره دارند. همچنین برای تعریف «ماتریس هسین» برای توابع چند متغیره از این قضیه و نتایج آن بسیار بهره‌برداری می‌شود.

به این منظور پیشنهاد می‌شود علاوه بر این متن، نوشتارهای دیگر مجله فرادرس با عنوان ماتریس هسین و خصوصیات آن — به زبان ساده و مشتق جزئی — به زبان ساده را مطالعه کنید. همچنین خواندن مطالب خواندن نوشتارهای توابع چند متغیره — به زبان ساده و روش‌های مشتق‌گیری — به همراه مثال نیز خالی از لطف نیست.

قضیه شوارتز و تقارن در مشتق دوم

در ریاضیات و حسابان چند متغیره، تقارن در مشتقات دوم که به آن برابری مشتقات جزئی نیز گفته می شود، برای یک تابع چند متغیره به کار رفته و این امکان را بوجود می‌آورد که با تعویض ترتیب گرفتن مشتقات جزئی یک تابع در شرایط خاص، نتایج یکسانی دریافت کرد. در حقیقت ترتیب مشتق‌گیری روی چنین توابعی، در حاصل تفاوتی ایجاد نمی‌کند. چنین حالتی را تقارن در مشتق‌گیری می‌گویند. به این ترتیب می‌توان جای عملگرهای مشتق بر حسب هر یک از متغیرها را در چنین توابعی تغییر داده و جابجا کرد. این امر خاصیت جابجایی در مشتق‌گیری نیز نامیده می‌شود.

فرض کنید تابعی چند متغیره به صورت $$f(x_1,x_2, \ldots,x_n)$$ با $$n$$ متغیر وجود دارد. اگر مشتقات جزئی یا پاره‌ای آن نسبت به $$x_i$$ همگی موجود بوده و بسته به اندیس $$i$$ مشخص شوند، آنگاه تقارن در قضیه شوارتز به این معنی است که مشتق مرتبه دوم که با نماد $$f_{ij}$$ نشان داده می‌شود، در رابطه زیر صدق کند.

$$ \large f_{ij} = f_{ji}$$

به این ترتیب ماتریس حاصل از مشتقات دوم، تشکیل یک ماتریس مربعی متقارن $$n \times n $$ خواهد داد که به «ماتریس هسین» معروف است. شرایطی که برای تابع $$f$$ باید در نظر گرفت تا در این تقارن در مشتق دوم صدق کند طبق «قضیه شوارتز» (Schwarz’s Theorem) مشخص می‌شود. قضیه شوارتز را گاهی «قضیه کلرو» (Clairaut’s theorem) یا «قضیه یانگ» (Young’s theorem) نیز می‌نامند.

نکته: در زمینه و حوزه معادلات دیفرانسیل جزئی چنین شرطی را به عنوان «شرط انتگرال‌پذیری شوارتز» (Schwarz Integrability Condition) می‌شناسند.

بیان تقارن در فرم مشتق‌ها

براساس نماد مشتق پاره‌ای، منظور از تقارن در قضیه شوارتز را می‌توان به صورت زیر نشان داد.

$$ \large { \displaystyle {\frac { \partial }{\partial x}} \left({\frac { \partial f}{ \partial y}} \right)\ =\ {\frac {\partial }{\partial y}} \left({ \frac{ \partial f}{ \partial x}} \right)}$$

با نماد مشتق دوم به صورت زیر رابطه تقارن را نمایش می‌دهند.

$$ \large  {\displaystyle \frac { \partial ^{2}\!f}{ \partial x\, \partial y}}\ =\ {\frac { \partial ^{2}\!f}{ \partial y\, \partial x}} $$

نماد دیگر برای این حالت نیز می‌تواند به صورت زیر باشد.

$$\large {\displaystyle \partial _{x} \partial _{y}f = \partial _{y} \partial _{x}f}$$

همچنین اگر نماد ترکیب عملگرهای دیفرانسیل به صورت $$D_i$$ را به کار ببریم، به رابطه زیر خواهیم رسید.

$$\large {\displaystyle D_{i}\circ D_{j} = D_{j}\circ D_{i}}$$

منظور از $$D_i$$، مشتق جزئی نسبت به $$x_i$$ است.

از این رابطه نتیجه می‌شود که عملگرهای دیفرانسیل با ضرایب ثابت، تولید شده توسط Di، یک «حلقه جابجایی» (Commutative Ring) ‌است. اما این موضوع فقط برای اپراتورها در دامنه‌ای از توابع کاملاً دیفرانسیل‌پذیر قابل اجرا است. به راحتی می‌توان تقارن را در مورد تک جمله‌ای‌ها نیز اعمال کرد، بنابراین چند جمله‌ای‌ها را در $$x_i$$ به عنوان دامنه در نظر می‌گیرند. در واقع «توابع هموار» (Smooth Function) دامنه معتبر دیگری در این زمینه هستند.

تاریخچه قضیه شوارتز

نتیجه برابری مشتقات جزئی با ترتیب‌های مختلف، تحت شرایط خاص، دارای سابقه طولانی است. لیستی از اثبات‌های پیشنهادی و البته ناموفق با ادعای اولیه «اویلر» (Euler) آغاز شد. او در سال ۱۷۴۰ مطلبی در این زمینه منتشر کرد. اگرچه قبلاً در سال 1721 «برنولی» (Bernoulli) نتیجه را بدون توجیه رسمی فرض کرده بود.

در همین بین، «کِلِرو» (Clariaut) یک اثبات پیشنهادی برای این قضیه در سال 1740 منتشر کرد، تا پایان قرن 18 هیچ تلاش دیگری برای اثبات این قضیه صورت نگرفت. پس از این دوره، تعدادی اثبات ناقص ارائه شد. اثبات «لاگرانژ» ( Lagrange) که در سال 1797 ارائه شده بود، توسط «کوشی» (Cauchy) در سال 1823، بهبود یافت، اما شرط پیوستگی مشتقات جزئی $$ {\displaystyle {\frac {\partial ^ {2} f} {\partial x ^ {2}}}} $$ و $$ {\displaystyle {\frac {\partial ^ {2} f} {\partial y ^ {2 }}}}$$ در آن  فرض شده بود.

تلاش های دیگر توسط «بلانژ» (Blanchet) در سال ۱۸۴۱، «داهامل» (Duhamel) در سال ۱۸۵۶، استرام (Strum) در سال ۱۸۵۷، «اشلومیچ» (Schlomilch) در سال ۱۸۶۲ و «برنارد» (Bernard) در سال ۱۸۶۴ انجام شد.

سرانجام در سال 1867، «لیندلف» (Lindelöf) به طور سیستماتیک تمام اثبات‌های قبلی را مورد بررسی قرار داد و توانست مثال نقضی ارائه کند که در آن قضیه تقارن برقرار نبود.

شش سال پس از آن، «شوارتز» (Schwarz) موفق شد اولین اثبات دقیق را ارائه دهد. «دینی» (Dini) بعداً با یافتن شرایط عمومی‌تر از شرایط شوارتز، در این امر سهیم شد. سرانجام یک نسخه کامل و بین نقص توسط «جردن» (Jordan) در سال 1883 ارائه گردید که هنوز هم اثبات آن در بیشتر کتابهای درسی مورد استفاده قرار می‌گیرد.

اثبات‌هایی نیز به صورت محدود توسط «لورن» (Laurent) در سال 1885، «پیانو» (Peano) در سال 1889 و 1893 ارائه گردید. «ادواردز» (Edwards)، «هاگ» (Haaag)، «وایتمور» (Whitetemore) و «ویوانتی » (Vivanti)  به همراه «پیرپونت» (Pierpont) در این زمینه ارائه کردند.

آخرین روش‌های اثبات و تعیین شرایط تابع برای قضیه شوارتز، در سال ۱۹۰۷ و توسط «هوبسون» (Hobson) و «یانگ» (Young) ارائه شد که شرایط ضعیف‌تری نسبت به اثبات شوارتز و دینی ارائه می‌کردند. همچنین «کاراتئودری» (Caratheodory) در سال ۱۹۱۸، اثباتی برمبنای «انتگرال لبگ» (Lebesgue Integral) ارائه کرد.

فرم رسمی قضیه شوارتز

قضیه شوارتز (یا قضیه کلرو) به فرم رسمی به صورت زیر بیان می‌شود.

فرض کنید، تابع F از $$\Omega$$ به مجموعه اعداد حقیقی تعریف شده باشد، بطوری که $$\Omega \subset R^n$$ باشد. اگر نقطه $$n$$ بُعدی $$p$$ دارای نقاط همسایگی از $$\Omega$$ باشند و تابع $$f$$ نیز دارای مشتق دوم پیوسته روی p باشد، آنگاه رابطه زیر برای هر $$i, j $$ در مجموعه اعداد طبیعی کمتر از $$n$$ برقرار است.

$$ \large i , j \in \{1 , 2 , \ldots , n \} $$

$$ \large {\displaystyle {\frac {\partial ^{2}}{\partial x_{i}\,\partial x_{j}}}f(\mathbf {p} )={\frac {\partial ^{2}}{\partial x_{j}\,\partial x_{i}}}f(\mathbf {p} ).} $$

توجه داشته باشید که در این حالت، مشتق‌های پاره‌ای تابع در نقطه p محاسبه شده‌اند.

یکی از روش‌های اثبات قضیه شوارتز در زمانی که $$n=2$$ و $$i=1$$ و $$j=2$$ باشد، توسط «قضیه گرین» (Green Theorem) و به کارگیری آن روی گرادیان تابع $$F$$ صورت می‌گیرد.

یک اثبات اولیه برای توابعی که روی یک زیر مجموعه باز از یک صفحه تعریف شده‌اند به صورت زیر انجام می‌شود. واضح است که ساده‌سازی و کاهش شرط‌های قضیه شوارتز، یک صفحه را ایجاد می‌کند.

فرض کنید که تابع $$f$$ یک تابع مشتق‌پذیر روی یک مستطیل به صورت بازه $$(a,b)$$ باشد و پیوستگی مشتق تابع نسبت به $$x$$ و $$y$$ را در نظر گرفته باشیم. به این ترتیب $$\partial _x \partial_y f $$ و $$\partial _y \partial _x f$$ هر دو پیوسته هستند. توابع زیر را برحسب تابع $$f$$ تعریف می‌کنیم.

$$ \large {\displaystyle {\begin{aligned}u\left( h,\,k \right) & = f\left( a + h,\,b + k \right) – f \left( a + h,\,b\right),\\ v \left( h,\,k \right) & = f \left( a + h,\,b + k \right) – f \left(a,\,b + k \right),\\ w \left(h ,\,k \right) & = f \left(a + h,\, b + k \right) -f \left( a+ h,\,b \right) -f \left( a , \, b + k \right) + f \left( a ,\, b \right) \end{aligned}}}$$

این توابع برای $$|h|$$ و $$|k| $$ کوچکتر از $$\epsilon >0$$ تعریف شده‌اند و داریم:

$$ \large {\displaystyle \left[ a – \varepsilon ,\, a + \varepsilon \right] \times \left[ b – \varepsilon ,\, b + \varepsilon \right] \subset \Omega }$$

به کمک «قضیه مقدار میانگین» (Mean Value Theorem) مقادیر $$\theta$$، $$\theta’$$ و $$\phi$$ و $$\phi’$$ روی بازه $$(0,1)$$ به شکل زیر قابل محاسبه هستند.

$$ \large {\displaystyle {\begin{aligned}w \left( h,\,k \right)& =u \left( h,\,k \right) – u \left( 0,\,k \right) =h\, \partial_{x}u \left( \theta h,\,k \right) \\ & =h\, \left[ \partial _{x}f \left( a+ \theta h,\,b+k \right) -\partial_{x}f \left( a+ \theta h,\,b \right) \right] \\&=hk\, \partial_{y} \partial_{x}f \left( a+ \theta h,\,b+ \theta ^{\prime }k \right) \\w \left(h,\,k\right) & = v\left( h,\,k \right) -v \left( h,\,0 \right) = k\,\partial _{y}v\left(h,\,\phi k \right) \\&=k\left[ \partial_{y}f \left(a + h,\,b + \phi k \right) – \partial_{y}f \left( a,\,b +\phi k \right) \right] \\ & =hk \,\partial_{x} \partial_{y}f \left( a + \phi^{\prime }h,\,b + \phi k \right)\end{aligned}}} $$

از آنجایی که $$h , k \neq 0 $$، معادله اول را می‌توانیم به $$hk$$‌ تقسیم کنیم. پس داریم:

$$ \large {\displaystyle {\begin{aligned}hk\,\partial_{y}\partial _{x}f \left(a + \theta h,\,b +\theta ^{\prime }k\right)& = hk\,\partial_{x}\partial_{y}f \left( a + \phi^{\prime }h ,\, b + \phi k \right), \\ \partial_{y}\partial_{x}f \left( a + \theta h ,\, b + \theta^{\prime }k \right) & = \partial_{x} \partial_{y} f \left(a + \phi^{\prime} h ,\ ,b + \phi k \right) \end{aligned}}}$$

این بار $$h , k $$ را به سمت صفر میل داده و در آخرین معادله قرار می‌دهیم. شرط پیوستگی مشتق‌های پاره‌ای برای تابع $$f$$ برای متغیرهای $$x,y$$ نتیجه‌ای به صورت زیر ایجاد می‌کند.

$$ \large {\displaystyle {\frac {\partial^{2}}{\partial x \partial y}} f \left( a,\,b\right) = {\frac {\partial^{2}}{ \partial y \partial x}}f \left(a,\,b \right)}$$

این اثبات در بسیاری از کتاب‌های کلاسیک مانند کتاب «اپوستول» (Apostol‌) و «رودین» (Rudin) دیده می‌شود.

اگرچه استنباط فوق ابتدایی است، اما می‌توان از منظر مفهومی‌تری به این رویکرد نیز نگریست تا نتیجه آشکارتر شود. در واقع عملگرهای تفاضل $$ {\displaystyle \Delta _ {x} ^ {t} ، \ ، \ ، \Delta _ {y} ^ {t}}$$ دارای خاصیت جابجایی بوده و در زمانی که $$t$$ به صفر نزدیک می‌شود، $$ {\displaystyle \Delta _ {x} ^ {t} f ، \ ، \ ، \Delta _ {y} ^ {t} f}$$ نیز به سمت $$ {\displaystyle \partial _ {x} f ، \ ، \ ، \partial _ {y} f }$$ میل می‌کنند. چنین عبارتی را برای عملگر مرتبه دوم نیز می‌توان در نظر گرفت.

در اینجا، برای $${\displaystyle z} $$ به عنوان یک بردار در صفحه و یک بردار جهت‌دار $$ {\displaystyle u} $$، عملگر تفاضلی به صورت زیر تعریف می‌شود.

$$ \large{\displaystyle \Delta _{u}^{t} f(z) = {f(z + tu) – f(z) \over t}}$$

طبق قضیه اساسی حسابان برای توابع $$f$$ از نوع $$C^1$$ روی یک فاصله باز مثل $$I$$ خواهیم داشت.

$$ \large {\displaystyle \int_{a}^{b}f^{ \prime } (x)\,dx = f(b) – f(a)}, \;\;\; (a,b) \subset I $$

در نتیجه

$$ \large {\displaystyle | f(b) – f(a) | \leq (b – a)\, \sup_{c \in (a,b)}| f^{ \prime }(c)| }$$

این یک نسخه کلی از «قضیه مقدار میانگین» (Mean Value Theorem) است. به یاد بیاورید که بحث مقدماتی در مورد حداکثر یا حداقل برای توابع با مقادیر حقیقی، نشان می‌دهد که اگر $$ {\displaystyle f}$$ در $$ {\displaystyle [a، b]}$$ پیوسته و در $$ {\displaystyle (a، b) } $$ مشتق‌پذیر باشد، یک نقطه‌ای مانند $$ {\displaystyle c} $$ در $$ {\displaystyle (a، b)} $$ وجود دارد به گونه ای که در رابطه زیر صدق می‌کند.

$$ \large {\displaystyle {f(b) – f(a) \over b – a} = f^{\prime }(c)}$$

برای توابع برداری که در آن $$ {\displaystyle V}$$ یک بردار با بُعد متناهی با فضای نرم‌دار است، نمی‌توان از رابطه بالا استفاده کرد. ولی از آنجایی که رابطه $$ {\displaystyle \inf f ^ {\prime} \leq f ^ {\prime} (c) \leq \sup f ^ {\prime}} $$ برقرار است، قضیه مقدار میانگین را برحسب نرم می‌توان نوشت.

$$ \large {\displaystyle \|f(b) – f(a) \| \leq (b – a)\, \sup_{c \in (a,b)}\| f^{\prime }(c)\|}$$

این نسخه از قضیه مقدار میانگین در کتاب «رودین»، «هرماندر» مورد بحث و بررسی قرار گرفته است.

برای توابعی که در $$C^2$$ قرار گرفته‌اند، باید از یک صفحه کمک گرفت. به این ترتیب تعریف زیر را در نظر می‌گیریم.

$$ \large D_1 = \partial_x $$

$$ \large D_2 = \partial_y $$

به این ترتیب به ازاء $$t \neq 0 $$ تساوی‌های زیر را فرض می‌گیریم.

$$ \large {\displaystyle \Delta_{1}^{t}f(x,y) = [f( x + t,y) – f(x,y)] /t } $$

$$ \large {\displaystyle \Delta_{2}^{t}f(x,y) = [f(x,y + t) – f(x,y)] /t }$$

سپس برای نقطه $$ {\displaystyle (x_ {0}، y_ {0})} $$ در مجموعه باز، از قضیه مقدار میانگین تعمیم یافته استفاده کرده و آن را در دو جا به کار می‌بریم.

$$ \large {\displaystyle \left | \Delta _ {1} ^ {t} \Delta _ {2} ^ {t} f (x_ {0}، y_ {0}) – D_{1} D_ {2} f (x_{0} ، y_{0}) \right | \leq }$$

$$ \large {\displaystyle  \sup _ {0 \leq s \leq 1} \left| \Delta _{1} ^ {t} D_ {2} f (x_ {0}، y_ {0} + ts) -D_ {1} D_ {2} f (x_ {0}، y_{0}) \right| \leq}$$

$$ \large {\displaystyle \sup _ {0 \leq r ، s \leq 1} \left| D_{1} D_{2} f (x_{0} + tr ، y_{0} + ts) – D_{1} D_{2} f (x_{0}، y_{0}) \right|}$$

بنابراین $$ {\displaystyle \Delta_ {1} ^ {t} \Delta_ {2} ^ {t} f (x_{0}، y_{0})}$$ زمانی که $$t$$ به سمت صفر می‌رود، به سمت $$ {\displaystyle D_{1} D_{2} f (x_{0}، y_{0})} $$ میل می‌کند.

از آنجا که عملگرهای تفاضل خاصیت جابجایی دارند، عملگرهای دیفرانسیل جزئی $$ {\displaystyle D_ {1}} $$ و $$ {\displaystyle D_ {2}}$$ نیز به همین شکل خواهند بود.

نکته: با به کار بردن دو بار قضیه مقدار میانگین برای $$ \theta$$ و $$\theta’$$ در بازه $$(0,10)$$، خواهیم داشت:

$$ \large {\displaystyle \Delta _{1}^{t} \Delta _{2}^{t} f(x_{0},y_{0}) = D_{1}D_{2} f(x_{0} + t \theta ,y_{0} + t \theta^{\prime })}$$

بنابراین اولین اثبات پایه‌ای را می‌توان با استفاده از عملگرهای تفاضل تفسیر کرد. برعکس، به جای استفاده از قضیه مقدار میانگین تعمیم یافته در اثبات دوم، می‌توان از قضیه مقدار میانگین کلاسیک استفاده کرد.

اثبات قضیه شوارتز به کمک انتگرال مکرر

خصوصیات «انتگرال‌های مکرر ریمان» (Repeated Riemann integrals) از یک تابع پیوسته مثل F روی یک مستطیل فشرده [a، b] × [c، d] به راحتی مشخص می‌شوند. پیوستگی یکنواخت تابع F بلافاصله پیوستگی توابع زیر را نتیجه می‌دهد.

$$\large {\displaystyle g(x) = \int _{c}^{d}F(x,y)\,dy} $$

$$\large {\displaystyle h(y) = \int _{a}^{b}F(x,y)\,dx}$$

در نتیجه خواهیم داشت:

$$ \large {\displaystyle \int _{a}^{b} \int _{c}^{d} F(x,y) \,dy \,dx = \int _{c}^{d} \int _{a}^{b} F(x,y)\,dx\,dy} $$

اگر تابع $$F$$ یک تابع مثبت باشد، این موضوع مثبت بودن انتگرال مکرر را نشان می‌دهد. تساوی فوق، حالت خاصی از «قضیه فوبینی» (Fubini’s Theorem) است. بخصوص زمانی که از نظریه اندازه استفاده نشود. می‌توان به سادگی اثباتی برای تساوی بالا براساس جمع‌های تقریبی ریمان نسبت به زیر بخش‌هایی از مستطیل اصلی ایجاد کرد.

برای اثبات قضیه کلرو یا همان قضیه شوارتز، فرض کنید که تابع $$f$$ یک تابع مشتق‌پذیر روی یک مجموعه باز مثل $$U$$ باشد. روی این مجموعه، مشتقات پاره‌ای $$\partial_x \partial_y f$$ و $$\partial_y \partial_x f$$ موجود و پیوسته هستند. بر اساس قضیه اساسی حسابان (Fundamental Theorem of Calculus) می‌توان نوشت:

$$ \large {\displaystyle \int_{c}^{d} \int_{a}^{b} \partial _{x} \partial_{y} f(x,y) \, dx \, dy = \int_{c}^{d} \partial_{y} f(b,y) -\partial_{y} f(a,y)\,dy = f(b,d) – f(a,d) – f(b,c) + f(a,c)} $$

و به طور مشابه به رابطه زیر رسید.

$$ \large {\displaystyle \int _{a}^{b}\int _{c}^{d} \partial_{y} \partial _{x} f(x,y) \,dy \, dx = \int _{a}^{b} \partial_{x} f(x,d) – \partial _{x} f(x,c)\, dx = f(b,d) – f(a,d) – f(b,c) + f(a,c)} $$

به ان ترتیب هر دو انتگرال مکرر با هم برابر هستند. از طرفی چون $$\partial_y\partial_xf(x,y)$$ پیوسته است، انتگرال مکرر دوم را می‌توان از طریق انتگرال اول روی $$x$$ و سپس روی $$y$$ بدست آورد.

اما انتگرال مکرر $$\partial_x\partial_yf – \partial_y\partial_xf$$ روی $$[a,b]\times ]c ,d ]$$ باید صفر شود. می‌دانیم که صفر بودن یک انتگرال مکرر برای تابع پیوسته $$F$$ روی همه مستطیل‌ها، نشانگر صفر بودن خود تابع $$F$$ است. در غیر اینصورت، تابع $$F$$ باید اکیدا مثبت و پیوسته روی یک مستطیل باشد که امکان‌پذیر نیست. در نتیجه $$\partial_x\partial_y f – \partial_y\partial_x f $$ باید صفر شوند. پس همه جا رابطه زیر برقرار خواهد بود.

$$ \large {\displaystyle \partial_x \partial_y f = \partial_y \partial_x f }$$

شرط کافی مشتق‌پذیری مضاعف

یک وضعیت ضعیف‌تر از پیوستگی مشتقات جزئی دوم (که برای اطمینان از تقارن کافی است)، این است که همه مشتقات جزئی، خود مشتق‌پذیر باشند. یک قضیه قوی‌تر در این زمینه که شرط جابجایی در مشتقات جزئی را مطرح می‌کند، توسط «پیانو» (Peano) در یادداشت کوتاهی در سال 1890 ارائه شده است. این موضوع را در ادامه مشاهده می‌کنید.

اگر تابع $$f: E \rightarrow R$$ روی یک مجموعه باز $$E \subset R^2$$ تعریف شده باشد و $$\partial_ f(x,y) $$ و $$\partial_{2,1}f(x,y)$$ روی همه $$E$$ موجود باشند، آنگاه $$\partial_{2,1}f$$ هم روی نقطه $$(x_0,y_0) \in E$$ پیوسته بوده و اگر $$\partial_2f(x,y_0)$$ در همسایگی $$x=x_0$$ موجود باشد، آنگاه $$\partial_{1,2}f$$ نیز در نقطه $$(x_0,y_0)$$ موجود بوده و داریم:

$$ \large \partial_{1,2}f(x_0,y_0) = \partial_{2,1}f(x_0 , y_0) $$

پیش‌نیاز پیوستگی

اگر تابع مشتقات جزئی پیوستگی نداشته باشد، خاصیت تقارن در مشتق دوم ممکن است برقرار نباشد. این موضوع در قضیه کلرو مشخص شده است. به عنوان یک مثال به تابعی به فرم زیر توجه کنید. این تابع اولین بار توسط «پیانو» معرفی شد.

$$ \large {\displaystyle f(x,\,y) = {\begin{cases} {\frac {xy \left(x^{2} – y^{2} \right) }{x^{2} + y^{2}}} &{\mbox{ for }}(x,\,y) \neq (0,\,0), \\ 0 & {\mbox{ for }}(x,\,y) =(0,\,0) \end{cases}}}$$

نمودار این تابع را در تصویر زیر مشاهده می‌کنید. این تابع در نقطه مبدا مختصات، دارای مشتق متقارن نیست.

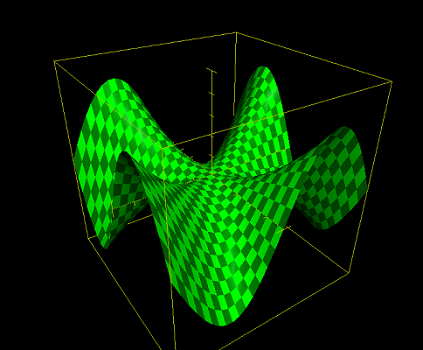
این موضوع را می‌توان با فرم یا مختصات قطبی تابع به صورت زیر نشان داد.

$$ \large {\displaystyle f (r \cos (\theta) , r \sin (\theta)) = r ^ {2} \sin (4 \theta)} $$

این تابع در همه جا پیوسته است. اما مشتقات آن در نقطه مبدا یعنی $$(0 ، 0)$$ را نمی توان از نظر جبری محاسبه کرد. بلکه حد نسبت رشد (مفهوم مشتق) آن در هر یکی از متغیرها نشان می‌دهد که تساوی‌ها زیر برقرار است.

$$ \large {\displaystyle \partial_{x} f|_{(0,0)} = \partial_{y} f|_{( 0,0)} = 0} $$

بنابراین نمودار $$z = f (x، y) $$ دارای یک خط مماس افقی در نقطه مبدا است و همچنین مشتقات پاره‌ای $$\partial_xf$$ و $$\partial_yf$$ موجود و در همه جا پیوسته هستند. البته مشتق دوم جزئی در این نقطه پیوسته نیست و همین موضوع باعث عدم برقراری رابطه جابجایی یا تقارن در مشتق‌های دوم می‌شود.

در حقیقت در طول محور افقی مشتق برحسب y به صورت $$ { \displaystyle \partial _ {y} f  |_ {(x، 0)} = x} $$ است. به همین ترتیب داریم:

$$ \large {\displaystyle  \partial_{x} \partial_{y}f |_{(0,0)} = \lim _{\varepsilon \rightarrow 0}{ \frac {\partial _{y} f|_{(\varepsilon ,0)} -\partial_{y}f |_{(0,0)}} {\varepsilon }} = 1} $$

در مقابل، در امتداد محور y، مشتق برحسب x به صورت $$ {\displaystyle \partial_ {x} f |_ {(0، y)} = – y} $$ است و داریم:

$$\large {\displaystyle \partial_ {y} \partial_ {x} f |_ {(0،0) } = – 1} $$

به این ترتیب امکان جابجایی مشتق‌گیری وجود ندارد. ولی در هر نقطه‌ای غیر از مرکز، این جابجایی در مشتق‌گیری برقرار بوده و تابع به صورت مشتق متقارن معرفی می‌شود.

این بار از دستگاه مختصات استوانه‌ای تابع استفاده می‌کنیم. طبق تعریف تابع گفته شده، به رابطه زیر خواهیم رسید.

$$ \large {\displaystyle f(r,\, \theta ) = {\frac {r^{2}\sin {4 \theta }}{4}}} $$

این فرم از تابع، نشان می‌دهد که این تابع دارای چهار نوسان است. به طور بصری، رفتار محلی تابع در نقطه مبدا یعنی $$(0 ، 0) $$ را نمی‌توان به عنوان یک فرم درجه دوم توصیف کرد و بنابراین ماتریس هسین نمی‌تواند متقارن باشد.

به طور کلی، جابجایی عملگر حد همیشه مجاز نیست و نمی‌توان حد را جابجا کرد. برای دو متغیر با مقداری نزدیک به مبدا، حد را به کمک رابطه‌های زیر مشخص می‌کنیم.

$$ \large {\displaystyle f(h,\,k) – f(h,\,0) – f(0,\,k) + f(0,\,0)} $$

به این ترتیب اگر ابتدا $$h$$ را به سمت صفر میل دهیم، نتیجه‌ای متفاوت نسبت به میل دادن ابتدا $$k$$ به سمت صفر حاصل می‌شود. این موضوع می‌تواند نمایانگر اهمیت تقارن در مشتق دوم و شرایط آن باشد.

این نوع مثال‌ها در نظریه آنالیز حقیقی نیز به کار می‌روند. مشخص است که نقطه‌ای که به دنبال مشتق آن هستیم مهم است. وقتی به عنوان یک تابع توزیع به مسئله نگاه می‌کنیم، مقادیر مشتق جزئی مرتبه دوم را می‌توان در یک مجموعه دلخواه از نقاط تغییر داد به شرطی که این نقاط دارای اندازه لبگ صفر باشند.

از آنجا که در مثال گفته شده ماتریس هسین به جز در نقطه مبدا، متقارن است می‌توان تابع را به عنوان یک «توزیع شوارتز» (Schwartz distribution) ‌در نظر گرفت.

کاربرد قضیه شوارتز در نظریه توزیع‌ها

نظریه توزیع‌ها (توابع تعمیم یافته) مشکلات تحلیلی را با تقارن از بین می‌برد. مشتق یک تابع انتگرا‌ل‌پذیر همیشه می‌تواند به عنوان یک تابع توزیع تعریف شود و تقارن مشتقات جزئی مخلوط شده، همیشه به عنوان یک تساوی در بین توزیع‌ها برقرار است.

استفاده از «انتگرال جزء به جزء» (Integration by Part) برای تعریف تمایز توزیع‌ها، تقارن را به «توابع آزمون» (Test Functions) برمی‌گرداند که هموار هستند و قطعاً ویژگی تقارن را برآورده می‌کنند. اگر بخواهیم موضوع را با جزئیات بیشتر توضیح دهیم، حالتی را در نظر می‌گیریم که $$f$$ یک توزیع و به عنوان یک اپراتور روی توابع آزمون نوشته شده و $$\phi$$ نیز یک تابع آزمون باشد. در این صورت می‌توان نوشت:

$$ \large {\displaystyle \left( D_{1}D_{2}f \right)[\phi ] = -\left( D_{2}f \right) \left[ D_{1}\phi \right] =f \left[ D_{2}D_{1}\phi \right] =f \left[ D_{1}D_{2} \phi \right] = -\left( D_{1}f \right) \left[ D_{2}\phi \right] =\left( D_{2}D_{1}f \right) [\phi ]}$$

رویکرد دیگر که براساس تبدیل فوریه یک تابع، تعریف می‌شود، با توجه به این نکته قابل بررسی است که جابجایی در مشتقات جزئی به صورت یک عملگر ضرب نشان داده شده که در نتیجه خاصیت جابجایی دارد.

کاربرد قضیه شوارتز در نظریه لی

عملگرهای دیفرانسیل مرتبه اول $$D_i$$ را در نظر بگیریم که در فضای اقلیدسی یک «عملگر بی‌نهایت» (Infinitesimal Operators) است. یعنی، یک گروه تبدیل را به موازات محور $$x_i$$ ایجاد می‌کنند. این گروه‌ها با یکدیگر قابل جابجایی هستند و بنابراین مولدهای بی‌نهایت (Infinitesimal Generators) نیز خواهند بود. پس براساس «براکت لی» (Lie Bracket) داریم:

$$\large [D_i, D_j] = 0$$

بازتاب این خاصیت نشان می‌دهد که «مشتق لی» (Lie derivation) در یک مختصات، نسبت به دیگری صفر است.

کاربرد قضیه شوارتز در فرم دیفرانسیلی

در این قسمت سوالی که در رابطه با قضیه شوارتز مطرح می‌شود این است که برای هر فرم دیفرانسیل $$\omega \ni \Omega^k(M)$$ در $$C^{\infty}$$، تحت چه شرایطی مقدار مشتق دوم برابر با صفر می‌شود. کلید اصلی برای اثبات یا حل این مسئله «قضیه شوارتز-کلرو» (Clairaut-Schwarz) است این قضیه یا مسئله، درحقیقت شرایطی را برای حل رابطه زیر بدست می‌دهد.

$$ \large d^2(\omega) = d(d\omega) = 0 $$

این بدان معنی است که هر فرم مشتق‌پذیر، بسته است. پس داریم:

$$ d\alpha = d(d\omega) = 0 \rightarrow d\alpha = 0 $$

در اواسط قرن هجدهم، تئوری فرم‌های دیفرانسیل برای اولین بار در ساده‌ترین حالت فرم نوع اول در صفحه، یعنی $$ {\displaystyle Adx + Bdy} $$ معین شد. در این رابطه $$A$$ و $$B$$، توابعی روی صفحه در نظر گرفته شدند. مطالعات روی فرم‌های نوع اول و دیفرانسیل‌های توابع، در مقاله «کلرو» در سال ۱۷۳۹ و ۱۷۴۰ مورد بحث قرار گرفت.

در آن مرحله تحقیقات وی به عنوان روش‌های حل «معادلات دیفرانسیل معمولی» (ordinary differential equations) تفسیر شد. به طور رسمی «کلرو» نشان داد که یک فرم نوع اول به صورت $$ {\displaystyle \omega = Adx + Bdy } $$ در یک مستطیل باز، بسته خواهد بود. به این معنی که $$ {\displaystyle d \omega = 0 } $$ است اگر و تنها اگر $$w$$ دارای فرم دیفرانسیل $$df$$ برای بعضی از توابع $$f$$ روی دیسک باشد. به منظور حل این مسئله، تابع $$f$$ را می‌توان به صورت فرمول انتگرال کوشی و به شکل زیر نوشت.

$$\large {\displaystyle f(x,y) = \int _{x_{0}}^{x} A(x,y) \,dx + \int_{y_{0}}^{y} B(x,y) \,dy}$$

در حالی که اگر $$ {\displaystyle \omega = df} $$ باشد، ویژگی بسته بودن $${\displaystyle d \omega = 0} $$ باعث بروز تساوی زیر خواهد شد.

$$ \large  {\displaystyle \partial _ { x} \partial _ {y} f = \partial _ {y} \partial _ {x} f} $$

رابطه بالا به زبان مدرن ریاضیاتی، یکی از نسخه‌های «لم پوانکاره» (Poincaré lemma) را بیان می‌کند.

خلاصه و جمع‌بندی

در این نوشتار با تقارن در مشتق دوم و انجام اولویت در مشتق‌گیری از توابع را مرور کرده و شرط امکان یا وجود جابجایی در عمل مشتق‌گیری را مورد بررسی قرار دادیم. قضیه مرتبط با تقارن در مشتق‌گیری به قضیه شوارتز معروف است که اثبات این قضیه در این متن نیز گنجانده شد. در انتها نیز کاربردهایی از قضیه شوارتز را بیان و مورد بحث قرار دادیم.